圆的对称性的中考复习
图片预览


文档简介
辅导:圆的对称性
主要内容:
1. 圆是轴对称图形,也是中心对称图形。
?????? 经过圆心的直线是对称轴。
?????? 圆心是它的对称中心。
2. 圆心角、弧、弦之间的关系
?????? 定理:在同一个圆中,如果圆心角相等,那么它们所对的弧相等,所对的弦也相等。
?????? 推论:在同一个圆中,如果两个圆心角、两条弧、两条弦中有一组量相等,那么它们所对应的其余各组量都分别相等。
?????? 如图,用几何语言表示如下:⊙O中,
(1)∵∠AOB=∠A'OB'
(3)∵AB=A'B'
? 5. 直径垂直于弦的性质(垂径定理)
?????? 垂直于弦的直径平分这条弦,并且平分弦所对的两条弧。
?????? 如图:几何语言
??????
【典型例题】
?例1. 如图,在Rt△ABC中,∠C=90°,AC=3,BC=4,以点C为圆心,CA为半径的圆与AB、BC分别交于点D、E。求AB、AD的长。
分析:求AB较简单,求弦长AD可先求AF。
解:
例2. 如图,⊙O中,弦AB=10cm,P是弦AB上一点,且PA=4cm,OP=5cm,求⊙O的半径。
分析:⊙O中已知弦长求半径,通常作弦心距构造直角三角形,利用勾股定理求解。
解:
?
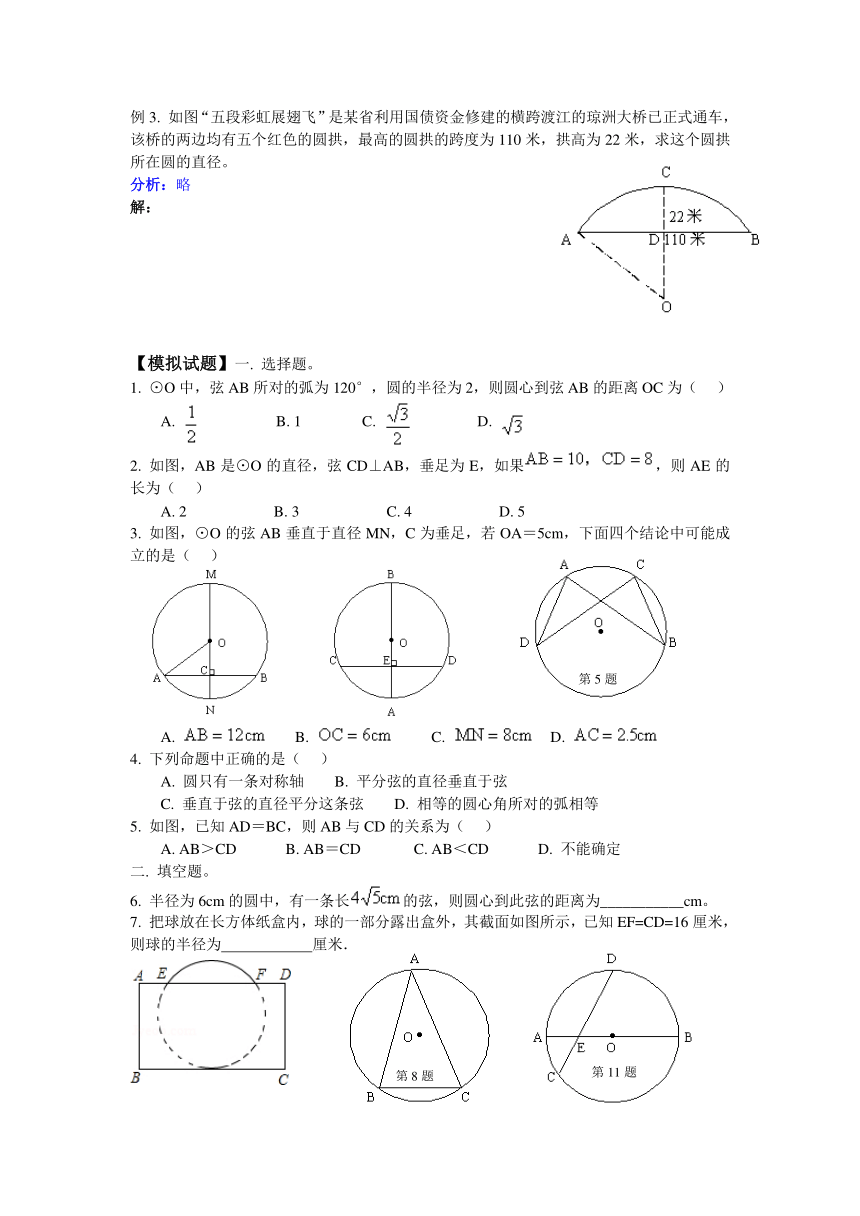
例3. 如图“五段彩虹展翅飞”是某省利用国债资金修建的横跨渡江的琼洲大桥已正式通车,该桥的两边均有五个红色的圆拱,最高的圆拱的跨度为110米,拱高为22米,求这个圆拱所在圆的直径。
分析:略
解:
??????
【模拟试题】一. 选择题。
1. ⊙O中,弦AB所对的弧为120°,圆的半径为2,则圆心到弦AB的距离OC为(??? )
?????? A. ?????????????????? B. 1?????????????? C. ??????????????? D.
2. 如图,AB是⊙O的直径,弦CD⊥AB,垂足为E,如果,则AE的长为(??? )
?????? A. 2????????????????????? B. 3????????????????????? C. 4????????????????????? D. 5
3. 如图,⊙O的弦AB垂直于直径MN,C为垂足,若OA=5cm,下面四个结论中可能成立的是(??? )
?????? A. ?? ?B. C. ????D.
4. 下列命题中正确的是(??? )
?????? A. 圆只有一条对称轴?????? B. 平分弦的直径垂直于弦
?????? C. 垂直于弦的直径平分这条弦?????? D. 相等的圆心角所对的弧相等
5. 如图,已知AD=BC,则AB与CD的关系为(??? )
?????? A. AB>CD?????????????B. AB=CD C. AB<CD?????????????D. 不能确定
二. 填空题。
6. 半径为6cm的圆中,有一条长的弦,则圆心到此弦的距离为___________cm。
7. 把球放在长方体纸盒内,球的一部分露出盒外,其截面如图所示,已知EF=CD=16厘米,则球的半径为 厘米.
8. 如图,∠A=30°,则B=___________。
9. 过⊙O内一点M的最长的弦为6cm,最短的弦长为4cm,则OM的长为___________。
10. ⊙O的半径为10cm,弦AB∥CD,AB=12cm,CD=16cm,则AB和CD的距离为___________。
11. ⊙O的直径AB和弦CD相交于点E,已知AE=1cm,EB=5cm,∠DEB=60°,则CD=___________。
三. 解答题。
?12. 如图,⊙O的直径为4cm,弦AB的长为,你能求出∠OAB的度数吗?写出你的计算过程。
13. 已知,⊙O的弦AB垂直于直径CD,垂足为F,点E在AB上,且EA=EC。
?????? 求证:
14. 如图,AB是⊙O的弦,AB长为8,P是⊙O上一个动点(不与A、B重合),过点O作OC⊥AP于点C,OD⊥PB于点D,则CD的长是怎么变化的?请说明理由。
15. 如图,⊙O上有三点A、B、C且AB=AC=6,∠BAC=120°,求⊙O的半径。
?
16. ⊙O的直径AB=15cm,有一条定长为9cm的动弦,CD在上滑动(点C和A、点D与B不重合),且CE⊥CD交AB于E,DF⊥CD交AB于F。
(1)求证:AE=BF;2)在动弦CD滑动过程中,四边形CDFE的面积是否为定值,若是定值,请给出证明,并求这个定值,若不是,请说明理由。
?
17. (2012上海)如图,在半径为2的扇形AOB中,∠AOB=90°,点C是弧AB上的一个动点(不与点A、B重合)OD⊥BC,OE⊥AC,垂足分别为D、E.
(1)当BC=1时,求线段OD的长;
(2)在△DOE中是否存在长度保持不变的边?如果存在,请指出并求其长度,如果不存在,请说明理由;
(3)设BD=x,△DOE的面积为y,求y关于x的函数关系式,并写出它的定义域.
【试题答案】
一. 选择题。
? 1. B??????????? 2. A??????????????????????? 3 D???????????? 4. C?????????????? 5. B
二. 填空题。
? 6. 4????????????????????????????????7. 10
8. 75°??????????????????????????? 9.
? 10. 2cm或14cm
? 11. cm(垂径定理与勾股定理)
三. 解答题。
? 12 解:过点O作OC⊥AB于C,则
?????? 又
??????
?????? ∴∠OAB=30°
? 13 证明:连结BC
?????? ∵AB⊥CD,CD为⊙O的直径 ∴BC=AC
?????? ∴∠CAB=∠CBA
?????? 又EA=EC∴∠CAB=∠ECA∴∠CBA=∠ECA
?????? ∴△AEC∽△ACB? ? 即
? 14. 解:略
? 15 解:连OA
?????? ∵AB=AC,? ∴OA⊥BC于D又∠BAC=120°
?????? ∴∠BAD=∠CAD=60°,∠B=∠C=30°
??????
?????? 设⊙O的半径为r,则 ∴r=6
? 16. (1)证明:如图,过O作OG⊥CD于G
?????? 则G为CD的中点
?????? 又EC⊥CD,FD⊥CD∴EC∥OG∥FD∴O为EF的中点,即OE=OF
?????? 又AB为⊙O的直径 ∴OA=OB ∴AE=BF(等式性质)
?????? (2)解:四边形CDFE面积是定值
?????? 证明:∵动弦CD滑动过程中条件EC⊥DC,FD⊥CD不变
?????? ∴CE∥DF不变 ∴四边形CDFE为直角梯形,且OG为中位线
?????? ∴S=OG·CD
?????? 连OC,由勾股定理有:
??????
?????? 又CD=9cm是定值
17、解答:解:(1)如图(1),∵OD⊥BC,
∴BD=BC=,∴OD==;
(2)如图(2),存在,DE是不变的.
连接AB,则AB==2,
∵D和E是中点,∴DE=AB=;
(3)如图(3),
∵BD=x,∴OD=,
∵∠1=∠2,∠3=∠4,∴∠2+∠3=45°,
过D作DF⊥OE.
∴DF=,EF=x,∴y=DF?OE=(0<x<).
主要内容:
1. 圆是轴对称图形,也是中心对称图形。
?????? 经过圆心的直线是对称轴。
?????? 圆心是它的对称中心。
2. 圆心角、弧、弦之间的关系
?????? 定理:在同一个圆中,如果圆心角相等,那么它们所对的弧相等,所对的弦也相等。
?????? 推论:在同一个圆中,如果两个圆心角、两条弧、两条弦中有一组量相等,那么它们所对应的其余各组量都分别相等。
?????? 如图,用几何语言表示如下:⊙O中,
(1)∵∠AOB=∠A'OB'
(3)∵AB=A'B'
? 5. 直径垂直于弦的性质(垂径定理)
?????? 垂直于弦的直径平分这条弦,并且平分弦所对的两条弧。
?????? 如图:几何语言
??????
【典型例题】
?例1. 如图,在Rt△ABC中,∠C=90°,AC=3,BC=4,以点C为圆心,CA为半径的圆与AB、BC分别交于点D、E。求AB、AD的长。
分析:求AB较简单,求弦长AD可先求AF。
解:
例2. 如图,⊙O中,弦AB=10cm,P是弦AB上一点,且PA=4cm,OP=5cm,求⊙O的半径。
分析:⊙O中已知弦长求半径,通常作弦心距构造直角三角形,利用勾股定理求解。
解:
?
例3. 如图“五段彩虹展翅飞”是某省利用国债资金修建的横跨渡江的琼洲大桥已正式通车,该桥的两边均有五个红色的圆拱,最高的圆拱的跨度为110米,拱高为22米,求这个圆拱所在圆的直径。
分析:略
解:
??????
【模拟试题】一. 选择题。
1. ⊙O中,弦AB所对的弧为120°,圆的半径为2,则圆心到弦AB的距离OC为(??? )
?????? A. ?????????????????? B. 1?????????????? C. ??????????????? D.
2. 如图,AB是⊙O的直径,弦CD⊥AB,垂足为E,如果,则AE的长为(??? )
?????? A. 2????????????????????? B. 3????????????????????? C. 4????????????????????? D. 5
3. 如图,⊙O的弦AB垂直于直径MN,C为垂足,若OA=5cm,下面四个结论中可能成立的是(??? )
?????? A. ?? ?B. C. ????D.
4. 下列命题中正确的是(??? )
?????? A. 圆只有一条对称轴?????? B. 平分弦的直径垂直于弦
?????? C. 垂直于弦的直径平分这条弦?????? D. 相等的圆心角所对的弧相等
5. 如图,已知AD=BC,则AB与CD的关系为(??? )
?????? A. AB>CD?????????????B. AB=CD C. AB<CD?????????????D. 不能确定
二. 填空题。
6. 半径为6cm的圆中,有一条长的弦,则圆心到此弦的距离为___________cm。
7. 把球放在长方体纸盒内,球的一部分露出盒外,其截面如图所示,已知EF=CD=16厘米,则球的半径为 厘米.
8. 如图,∠A=30°,则B=___________。
9. 过⊙O内一点M的最长的弦为6cm,最短的弦长为4cm,则OM的长为___________。
10. ⊙O的半径为10cm,弦AB∥CD,AB=12cm,CD=16cm,则AB和CD的距离为___________。
11. ⊙O的直径AB和弦CD相交于点E,已知AE=1cm,EB=5cm,∠DEB=60°,则CD=___________。
三. 解答题。
?12. 如图,⊙O的直径为4cm,弦AB的长为,你能求出∠OAB的度数吗?写出你的计算过程。
13. 已知,⊙O的弦AB垂直于直径CD,垂足为F,点E在AB上,且EA=EC。
?????? 求证:
14. 如图,AB是⊙O的弦,AB长为8,P是⊙O上一个动点(不与A、B重合),过点O作OC⊥AP于点C,OD⊥PB于点D,则CD的长是怎么变化的?请说明理由。
15. 如图,⊙O上有三点A、B、C且AB=AC=6,∠BAC=120°,求⊙O的半径。
?
16. ⊙O的直径AB=15cm,有一条定长为9cm的动弦,CD在上滑动(点C和A、点D与B不重合),且CE⊥CD交AB于E,DF⊥CD交AB于F。
(1)求证:AE=BF;2)在动弦CD滑动过程中,四边形CDFE的面积是否为定值,若是定值,请给出证明,并求这个定值,若不是,请说明理由。
?
17. (2012上海)如图,在半径为2的扇形AOB中,∠AOB=90°,点C是弧AB上的一个动点(不与点A、B重合)OD⊥BC,OE⊥AC,垂足分别为D、E.
(1)当BC=1时,求线段OD的长;
(2)在△DOE中是否存在长度保持不变的边?如果存在,请指出并求其长度,如果不存在,请说明理由;
(3)设BD=x,△DOE的面积为y,求y关于x的函数关系式,并写出它的定义域.
【试题答案】
一. 选择题。
? 1. B??????????? 2. A??????????????????????? 3 D???????????? 4. C?????????????? 5. B
二. 填空题。
? 6. 4????????????????????????????????7. 10
8. 75°??????????????????????????? 9.
? 10. 2cm或14cm
? 11. cm(垂径定理与勾股定理)
三. 解答题。
? 12 解:过点O作OC⊥AB于C,则
?????? 又
??????
?????? ∴∠OAB=30°
? 13 证明:连结BC
?????? ∵AB⊥CD,CD为⊙O的直径 ∴BC=AC
?????? ∴∠CAB=∠CBA
?????? 又EA=EC∴∠CAB=∠ECA∴∠CBA=∠ECA
?????? ∴△AEC∽△ACB? ? 即
? 14. 解:略
? 15 解:连OA
?????? ∵AB=AC,? ∴OA⊥BC于D又∠BAC=120°
?????? ∴∠BAD=∠CAD=60°,∠B=∠C=30°
??????
?????? 设⊙O的半径为r,则 ∴r=6
? 16. (1)证明:如图,过O作OG⊥CD于G
?????? 则G为CD的中点
?????? 又EC⊥CD,FD⊥CD∴EC∥OG∥FD∴O为EF的中点,即OE=OF
?????? 又AB为⊙O的直径 ∴OA=OB ∴AE=BF(等式性质)
?????? (2)解:四边形CDFE面积是定值
?????? 证明:∵动弦CD滑动过程中条件EC⊥DC,FD⊥CD不变
?????? ∴CE∥DF不变 ∴四边形CDFE为直角梯形,且OG为中位线
?????? ∴S=OG·CD
?????? 连OC,由勾股定理有:
??????
?????? 又CD=9cm是定值
17、解答:解:(1)如图(1),∵OD⊥BC,
∴BD=BC=,∴OD==;
(2)如图(2),存在,DE是不变的.
连接AB,则AB==2,
∵D和E是中点,∴DE=AB=;
(3)如图(3),
∵BD=x,∴OD=,
∵∠1=∠2,∠3=∠4,∴∠2+∠3=45°,
过D作DF⊥OE.
∴DF=,EF=x,∴y=DF?OE=(0<x<).
同课章节目录
