浙教版数学八年级下册 4.2平行四边形及其性质 课件(共14张PPT)
文档属性
| 名称 | 浙教版数学八年级下册 4.2平行四边形及其性质 课件(共14张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 202.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-12 19:25:33 | ||
图片预览





文档简介
(共14张PPT)
平行四边形的性质
B
C
A
D
我们学过平行四边形有哪些性质
定理 1 平行四边形的两组对边分别相等.
定义 平行四边形的两组对边分别平行.
定理 2 平行四边形的两组对角分别相等.
回顾
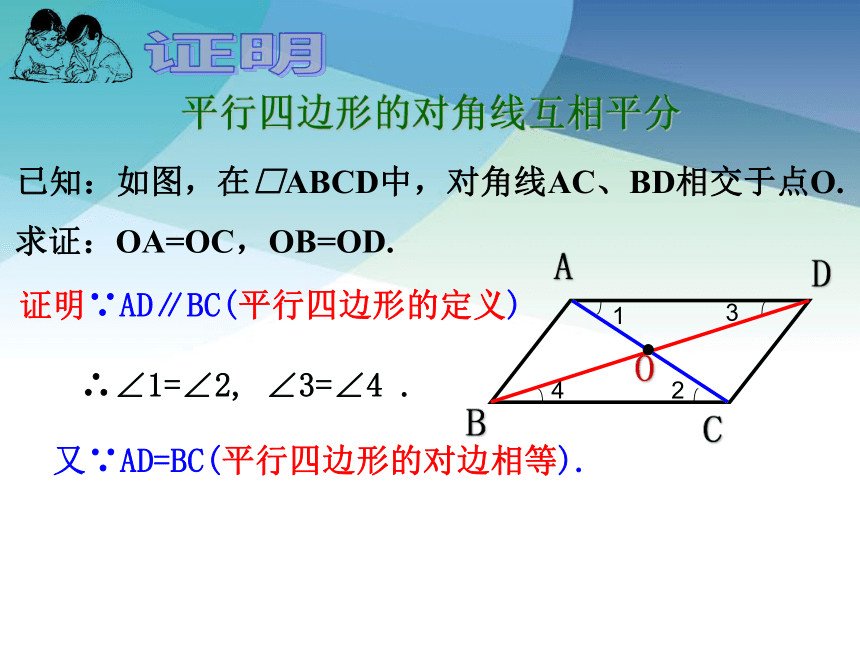
已知:如图,在□ABCD中,对角线AC、BD相交于点O.
求证:OA=OC,OB=OD.
B
A
C
D
3
4
1
2
O
证明∵AD∥BC(平行四边形的定义)
∴∠1=∠2, ∠3=∠4 .
又∵AD=BC(平行四边形的对边相等).
平行四边形的对角线互相平分
证明
平行四边形的性质
几何语言:
定理2:平行四边形的对角线互相平分
∵ 四边形ABCD是平行四边形
∴ OA=OC,OB=OD.(平行四边形的对角线互相平分)
在 ABCD中,
OA=OC,OB=OD.(平行四边形的对角线互相平分)
或
或
AC=2AO=2CO,BD=2BO=2DO
1、如图,在 ABCD中,AC与BD相交于点O,
(1)若AC=18cm,BD=24cm,则AO= , BO= .
又若AB=13厘米,则△COD的周长为 。
(2)若△AOB的周长为30cm, AB=12cm,则对角线AC与BD的和是 。
2.如图:平行四边形ABCD中, AC、BD相交于点O, AB=8, 则以下两条线段长能作为平行四边形的对角线的长的是( )
A. 4, 12 B. 6, 8 C. 8, 26 D. 12, 20
9cm
12cm
34cm
36cm
D
练一练
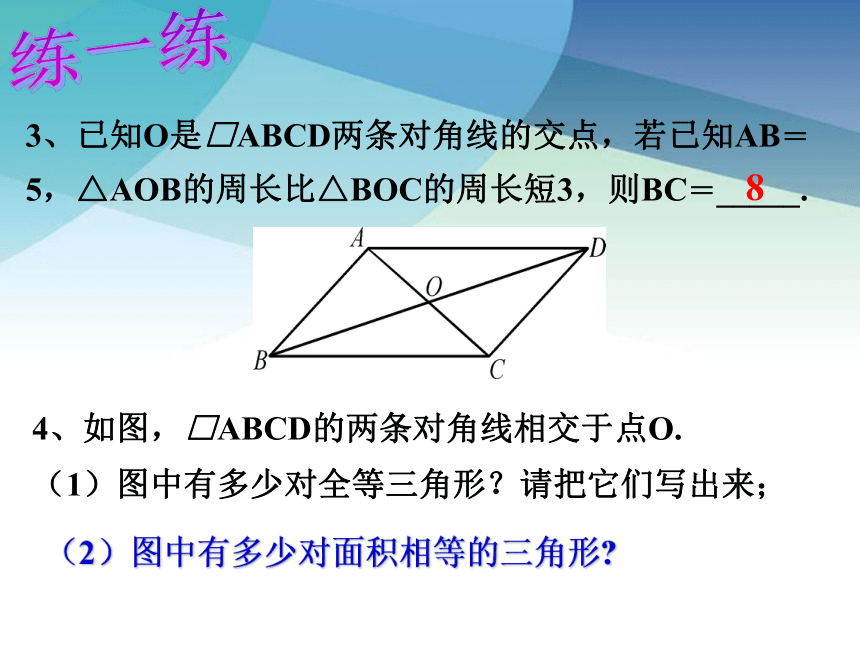
3、已知O是□ABCD两条对角线的交点,若已知AB= 5,△AOB的周长比△BOC的周长短3,则BC=_____.
8
练一练
4、如图,□ABCD的两条对角线相交于点O.
(1)图中有多少对全等三角形?请把它们写出来;
(2)图中有多少对面积相等的三角形
例1、已知:如图,□ABCD的对角线AC、BD交于点O。过点O作直线EF,分别交AB、CD于点E、F。
求证:OE=OF
A
B
C
D
F
E
O
证明∵AB∥CD
∴∠ODF=∠OBE
∴△DOF≌△BOE(ASA)
∴OD=OB
(平行四边形的对边平行)
(平行四边形的对角线互相平分)
∵ 四边形ABCD是平行四边形
在△DOF和△BOE中
∴OE=OF
改变直线EF的位置,OE=OF还成立吗
∠ODF=∠OBE
OD=OB
∠DOF=∠BOE
A
B
D
O
E
F
A
B
C
D
O
E
F
A
B
C
D
O
E
F
C
A
B
C
D
O
E
F
这些图形中被直线EF分割而成的两部分面积有怎样的数量关系?
过对角线交点的任一条直线将平行四边形的面积两等分
议一议
有一块平行四边形的草地,学校想在中间留一条小路,把它分成面积相等的两块,请你来想想,可以怎样分?有多少种分法?
有无数种分法,分割线只要过对角线的交点
想一想
一块草地中间有一水井,为了浇水的方便,经过水井修一条小路,并且把草地分成面积相等的两部分,同学们,你能画出小路的位置吗?
B
M
C
●
D
A
O
画一画
B
A
C
D
O
E
F
求证:△BOE≌△DOF.
证明:∵OB=OD ,OA=OC
∴OE=OF.
又∵ OE= OA, OF= OC(中点的定义)
1、已知:如图,□ABCD的对角线AC、BD交于点O,E、F分别是OA、OC的中点。
(平行四边形的对角线互相平分)
做一做
A
B
E
F
D
C
O
2、如图所示,已知□ABCD和□EBFD的顶点A、E、F、C在同一条直线AC上。请问:AE与CF有怎样的数量关系?请说明理由.
做一做
例2、如图,在□ABCD中,对角线AC、BD交于点E,AC⊥BC,AC=4,AB=5,求BD的长。
A
B
C
D
E
解:∵ AC⊥BC
∴BC2=AB2-AC2=25-16=9
(勾股定理)
∴ BC=3
∵ 四边形ABCD是平行四边形
∴CE= AC=2,BD=2BE
∴
∴BD=2BE=
(平行四边形对角线互相平分)
(勾股定理)
你还有别的方法吗
F
谢谢!
平行四边形的性质
B
C
A
D
我们学过平行四边形有哪些性质
定理 1 平行四边形的两组对边分别相等.
定义 平行四边形的两组对边分别平行.
定理 2 平行四边形的两组对角分别相等.
回顾
已知:如图,在□ABCD中,对角线AC、BD相交于点O.
求证:OA=OC,OB=OD.
B
A
C
D
3
4
1
2
O
证明∵AD∥BC(平行四边形的定义)
∴∠1=∠2, ∠3=∠4 .
又∵AD=BC(平行四边形的对边相等).
平行四边形的对角线互相平分
证明
平行四边形的性质
几何语言:
定理2:平行四边形的对角线互相平分
∵ 四边形ABCD是平行四边形
∴ OA=OC,OB=OD.(平行四边形的对角线互相平分)
在 ABCD中,
OA=OC,OB=OD.(平行四边形的对角线互相平分)
或
或
AC=2AO=2CO,BD=2BO=2DO
1、如图,在 ABCD中,AC与BD相交于点O,
(1)若AC=18cm,BD=24cm,则AO= , BO= .
又若AB=13厘米,则△COD的周长为 。
(2)若△AOB的周长为30cm, AB=12cm,则对角线AC与BD的和是 。
2.如图:平行四边形ABCD中, AC、BD相交于点O, AB=8, 则以下两条线段长能作为平行四边形的对角线的长的是( )
A. 4, 12 B. 6, 8 C. 8, 26 D. 12, 20
9cm
12cm
34cm
36cm
D
练一练
3、已知O是□ABCD两条对角线的交点,若已知AB= 5,△AOB的周长比△BOC的周长短3,则BC=_____.
8
练一练
4、如图,□ABCD的两条对角线相交于点O.
(1)图中有多少对全等三角形?请把它们写出来;
(2)图中有多少对面积相等的三角形
例1、已知:如图,□ABCD的对角线AC、BD交于点O。过点O作直线EF,分别交AB、CD于点E、F。
求证:OE=OF
A
B
C
D
F
E
O
证明∵AB∥CD
∴∠ODF=∠OBE
∴△DOF≌△BOE(ASA)
∴OD=OB
(平行四边形的对边平行)
(平行四边形的对角线互相平分)
∵ 四边形ABCD是平行四边形
在△DOF和△BOE中
∴OE=OF
改变直线EF的位置,OE=OF还成立吗
∠ODF=∠OBE
OD=OB
∠DOF=∠BOE
A
B
D
O
E
F
A
B
C
D
O
E
F
A
B
C
D
O
E
F
C
A
B
C
D
O
E
F
这些图形中被直线EF分割而成的两部分面积有怎样的数量关系?
过对角线交点的任一条直线将平行四边形的面积两等分
议一议
有一块平行四边形的草地,学校想在中间留一条小路,把它分成面积相等的两块,请你来想想,可以怎样分?有多少种分法?
有无数种分法,分割线只要过对角线的交点
想一想
一块草地中间有一水井,为了浇水的方便,经过水井修一条小路,并且把草地分成面积相等的两部分,同学们,你能画出小路的位置吗?
B
M
C
●
D
A
O
画一画
B
A
C
D
O
E
F
求证:△BOE≌△DOF.
证明:∵OB=OD ,OA=OC
∴OE=OF.
又∵ OE= OA, OF= OC(中点的定义)
1、已知:如图,□ABCD的对角线AC、BD交于点O,E、F分别是OA、OC的中点。
(平行四边形的对角线互相平分)
做一做
A
B
E
F
D
C
O
2、如图所示,已知□ABCD和□EBFD的顶点A、E、F、C在同一条直线AC上。请问:AE与CF有怎样的数量关系?请说明理由.
做一做
例2、如图,在□ABCD中,对角线AC、BD交于点E,AC⊥BC,AC=4,AB=5,求BD的长。
A
B
C
D
E
解:∵ AC⊥BC
∴BC2=AB2-AC2=25-16=9
(勾股定理)
∴ BC=3
∵ 四边形ABCD是平行四边形
∴CE= AC=2,BD=2BE
∴
∴BD=2BE=
(平行四边形对角线互相平分)
(勾股定理)
你还有别的方法吗
F
谢谢!
同课章节目录
- 第一章 二次根式
- 1.1 二次根式
- 1.2 二次根式的性质
- 1.3 二次根式的运算
- 第二章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程的应用
- 2.4 一元二次方程根与系数的关系(选学)
- 第三章 数据分析初步
- 3.1 平均数
- 3.2 中位数和众数
- 3.3 方差和标准差
- 第四章 平行四边形
- 4.1 多边形
- 4.2 平行四边形
- 4.3 中心对称
- 4.4 平行四边形的判定
- 4.5 三角形的中位线
- 4.6 反证法
- 第五章 特殊平行四边形
- 5.1 矩形
- 5.2 菱形
- 5.3 正方形
- 第六章 反比例函数
- 6.1 反比例函数
- 6.2 反比例函数的图象和性质
- 6.3 反比例函数的应用
