4.4平行四边形的判定 同步练习(含解析)
文档属性
| 名称 | 4.4平行四边形的判定 同步练习(含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-12 21:17:28 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
浙教版八年级下 4.4平行四边形的判定定理同步练习
一.选择题
1.(2021春 麦积区期末)在四边形ABCD中,AB∥CD,再添加下列其中一个条件后,四边形ABCD不一定是平行四边形的是( )
A.AB=CD B.AD=BC C.AD∥BC D.∠A=∠C
2.(2021春 娄星区校级期中)下列条件中,不能判定一个四边形为平行四边形的是( )
A.一组对边相等且平行 B.一组对边平行,另一组对边相等
C.两条对角线互相平分 D.两组对边分别相等
3.(2022 天河区一模)如图, ABCD中,E,F分别在边BC,AD上,添加选项中的条件后不能判定四边形AECF是平行四边形的是( )
A.BE=DF B.AE∥CF C.AF=EC D.AE=EC
4.(2022春 金华月考)如图,四边形ABCD的对角线AC,BD交于点O,则不能判断四边形ABCD是平行四边形的是( )
A.OB=OD,OA=OC B.AD∥BC,AB=CD
C.AB∥CD,AD∥BC D.AB∥CD,AB=CD
5.(2021秋 招远市期末)如图,在四边形ABCD中,AB∥CD,BC∥AD,且AD=DC,则下列说法:
①四边形ABCD是平行四边形; ②AB=BC;③AC⊥BD ④AC平分∠BAD;
⑤若AC=6,BD=8,则四边形ABCD的面积为24.
其中正确的有( )
A.2个 B.3个 C.4个 D.5个
6.(2012春 浦东新区期末)如图,已知四边形ABCD的面积为8cm2,AB∥CD,AB=CD,E是AB的中点,那么△AEC的面积是( )
A.4cm2 B.3cm2 C.2cm2 D.1cm2
7.(2021 霍邱县一模)如图,E是平行四边形ABCD的边AD的延长线上一点,连接BE交CD于点F,连接CE,BD.添加以下条件,仍不能判定四边形BCED为平行四边形的是( )
A.∠ABD=∠DCE B.∠AEC=∠CBD C.EF=BF D.∠AEB=∠BCD
8.(2021春 郧西县期末)下列能够判定四边形ABCD为平行四边形的条件是( )
A.AB∥CD,AD=BC B.∠A=∠B,∠C=∠D
C.AB=AD,CB=CD D.AB=CD,AD=BC
9.(2021春 雁塔区校级月考)如图,四边形ABCD的对角线AC、BD交于点O,下列条件:①∠BAD=∠BCD,∠ABC=∠ADC;②∠ABC=∠ADC,AB∥CD;③AB∥CD,OB=OD;④AB=CD,OA=OC,能判定四边形ABCD为平行四边形的有( )
A.1个 B.2个 C.3个 D.4个
10.(2021春 邗江区校级期中)如图,在Rt△ABC中,∠B=90°,AB=3,AC=5,点D在BC上,以AC为对角线的所有 ADCE中,DE最小的值是( )
A.3 B.4 C.2 D.1
二.填空题
11.(2021春 雁塔区校级月考)已知平面直角坐标系内有四个点A(0,3),B(0,﹣1),C(3,4),D(3,y).若以点A,B,C,D为顶点的四边形是平行四边形,则y的值为 .
12.(2021春 西湖区校级期中)如图,在 ABCD中,AC,BD相交于点O,点E,F在对角线BD上,有下列条件:①BF=DE;②AE=CF;③∠EAB=∠FCD;④AF∥CE.其中一定能判定四边形AECF是平行四边形的是 .
13.(2021春 商河县校级期末)如图, ABCD中,点E在CD的延长线上,AE∥BD,EC=4,则AB的长是 .
14.(2021春 娄底期末)如图,在平行四边形ABCD中,E,F两点均在对角线AC上.要使四边形BEDF为平行四边形,在不添加辅助线的情况下,需要增加的一个条件是 (写出一个即可).
15.(2021秋 栖霞市期末)在△ABC中,∠C=90°,AC=6,BC=8,若以A,B,C,D为顶点的四边形是平行四边形,则此平行四边形的周长为 .
16.(2021春 路南区期中)如图,在四边形ABCD中,AB∥DC,AD=BC=6,DC=9,AB=15,点P从点A出发以2个单位/s的速度沿AD→DC向终点C运动,同时点Q从点B出发,以1个单位/s的速度沿BA向终点A运动.当有一点到达终点时,点P、Q就停止运动.当运动时间为 s时,四边形PQBC为平行四边形.
三.解答题
17.(2021秋 龙岗区校级期末)已知:如图,在平行四边形ABCD中,E,F分别是AB,CD的中点.
求证:(1)△AFD≌△CEB;
(2)四边形AECF是平行四边形.
18.(2021 道外区三模)如图,在平行四边形ABCD中.点E在AD边上,点F在BC边上,且AE=CF,连接AF、BE相交于点M,连接CE、DF相交于点.
(1)如图1,求证:四边形EMFN为平行四边形;
(2)如图2,连接MN,若E是AD的中点,在不添加任何辅助线的情况下,请直接写出图2中以MN为边的所有平行四边形.
19.(2022春 九龙坡区校级月考)在四边形ABCD中,AC、BD交于点O,AD∥BC,BO=DO.
(1)证明:四边形ABCD是平行四边形;
(2)过点O作OE⊥BD交BC于点E,连接DE.若∠CDE=∠CBD=15°,求∠ABC的度数.
20.(2022春 泰州月考)如图所示,△ABC≌△EAD,点E在BC上.
(1)求证:四边形ABCD是平行四边形;
(2)若∠B:∠CAD=5:4,AE⊥ED,求∠EDC的度数.
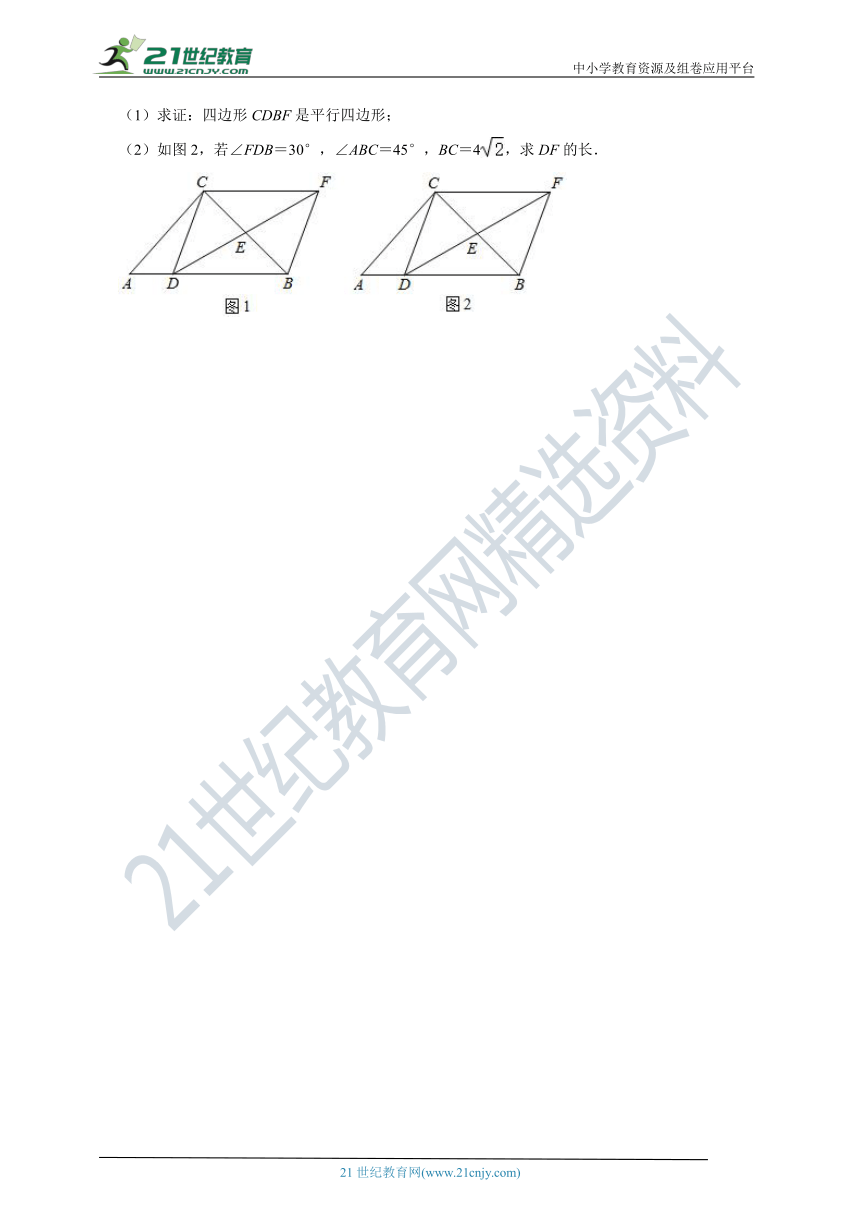
21.(2021 香坊区三模)如图1,在△ABC中,D是AB边上任意一点,E是BC边中点,过点C作AB的平行线,交DE的延长线于点F,连接BF,CD.
(1)求证:四边形CDBF是平行四边形;
(2)如图2,若∠FDB=30°,∠ABC=45°,BC=4,求DF的长.
答案与解析
一.选择题
1.(2021春 麦积区期末)在四边形ABCD中,AB∥CD,再添加下列其中一个条件后,四边形ABCD不一定是平行四边形的是( )
A.AB=CD B.AD=BC C.AD∥BC D.∠A=∠C
【解析】解:A、∵AB∥CD,若AB=CD,则四边形ABCD是平行四边形,故A选项不符合题意;
B、∵AB∥CD,若AD=BC,则四边形ABCD可能是等腰梯形,不一定是平行四边形,故B选项符合题意;
C、∵AB∥CD,若AD∥BC,则四边形ABCD是平行四边形,故C选项不符合题意;
D、∵AB∥CD,若∠A=∠C,则四边形ABCD是平行四边形,故D选项不符合题意;
故选:B.
2.(2021春 娄星区校级期中)下列条件中,不能判定一个四边形为平行四边形的是( )
A.一组对边相等且平行 B.一组对边平行,另一组对边相等
C.两条对角线互相平分 D.两组对边分别相等
【解析】解:A、一组对边相等且平行的四边形是平行四边形,故本选项不符合题意;
B、一组对边平行且另一组对边相等的四边形不一定是平行四边形,可能是等腰梯形,故本选项符合题意;
C、两条对角线互相平分是平行四边形,故本选项不符合题意;
D、两组对边分别相等的四边形是平行四边形,故本选项不符合题意;
故选:B.
3.(2022 天河区一模)如图, ABCD中,E,F分别在边BC,AD上,添加选项中的条件后不能判定四边形AECF是平行四边形的是( )
A.BE=DF B.AE∥CF C.AF=EC D.AE=EC
【解析】解:A、∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC,
∵BE=DF,
∴AF=CE,
∴四边形AECF是平行四边形,故选项A不符合题意;
B、∵四边形ABCD是平行四边形,
∴AD∥BC,
∵AE∥CF,
∴四边形AECF是平行四边形,故选项B不符合题意;
C、∵四边形ABCD是平行四边形,
∴AD∥BC,
∵AF=EC,
∴四边形AECF是平行四边形,故选项C不符合题意;
D、∵四边形ABCD是平行四边形,
∴AD∥BC,
由AE=EC,不能判定四边形AECF是平行四边形,故选项D符合题意;
故选:D.
4.(2022春 金华月考)如图,四边形ABCD的对角线AC,BD交于点O,则不能判断四边形ABCD是平行四边形的是( )
A.OB=OD,OA=OC B.AD∥BC,AB=CD
C.AB∥CD,AD∥BC D.AB∥CD,AB=CD
【解析】解:A、∵OB=OD,OA=OC,∴四边形ABCD是平行四边形,故此选项不合题意;
B、∵AD∥BC,AB=CD,不能判断四边形ABCD是平行四边形,故此选项符合题意;
C、∵AB∥CD,AD∥BC,∴四边形ABCD是平行四边形,故此选项不合题意;
D、∵AB∥CD,AB=CD,∴四边形ABCD是平行四边形,故此选项不合题意;
故选:B.
5.(2021秋 招远市期末)如图,在四边形ABCD中,AB∥CD,BC∥AD,且AD=DC,则下列说法:
①四边形ABCD是平行四边形; ②AB=BC; ③AC⊥BD ④AC平分∠BAD;
⑤若AC=6,BD=8,则四边形ABCD的面积为24.
其中正确的有( )
A.2个 B.3个 C.4个 D.5个
【解析】解:∵AB∥CD,BC∥AD,
∴四边形ABCD是平行四边形,故①正确;
∵AD=DC,
∴平行四边形ABCD是菱形,
∴AB=BC,AC⊥BD,AC平分∠BAD,故②③④正确,
∵AC=6,BD=8,
∴菱形ABCD的面积=AC×BD=×6×8=24,故⑤正确;
正确的个数有5个,
故选:D.
6.(2012春 浦东新区期末)如图,已知四边形ABCD的面积为8cm2,AB∥CD,AB=CD,E是AB的中点,那么△AEC的面积是( )
A.4cm2 B.3cm2 C.2cm2 D.1cm2
【解析】解:∵AB∥CD,AB=CD,
∴四边形ABCD是平行四边形,
∴S△ADC=S△ABC=×8=4,
∵E是AB的中点,
∴S△AEC=S△ABC=×4=2cm2,
故选:C.
7.(2021 霍邱县一模)如图,E是平行四边形ABCD的边AD的延长线上一点,连接BE交CD于点F,连接CE,BD.添加以下条件,仍不能判定四边形BCED为平行四边形的是( )
A.∠ABD=∠DCE B.∠AEC=∠CBD C.EF=BF D.∠AEB=∠BCD
【解析】解:A、∵四边形ABCD是平行四边形,
∴AD∥BC,AB∥CD,
∴DE∥BC,∠ABD=∠CDB,
∵∠ABD=∠DCE,
∴∠DCE=∠CDB,
∴BD∥CE,
∴四边形BCED为平行四边形,故A不符合题意;
B、∵AE∥BC,
∴∠DEC+∠BCE=∠EDB+∠DBC=180°,
∵∠AEC=∠CBD,
∴∠BDE=∠BCE,
∴四边形BCED为平行四边形,故B不符合题意,
C、∵DE∥BC,
∴∠DEF=∠CBF,
在△DEF与△CBF中,
,
∴△DEF≌△CBF(ASA),
∴DF=CF,
∵EF=BF,
∴四边形BCED为平行四边形,故C不符合题意;
D、∵AE∥BC,
∴∠AEB=∠CBF,
∵∠AEB=∠BCD,
∴∠CBF=∠BCD,
∴CF=BF,
同理,EF=DF,
∴不能判定四边形BCED为平行四边形;故D符合题意;
故选:D.
8.(2021春 郧西县期末)下列能够判定四边形ABCD为平行四边形的条件是( )
A.AB∥CD,AD=BC B.∠A=∠B,∠C=∠D
C.AB=AD,CB=CD D.AB=CD,AD=BC
【解析】解:如图所示:
A、∵AB∥CD,AD=BC,不符合“一组对边平行且相等的四边形是平行四边形”,
∴不能判定四边形ABCD是平行四边形,故本选项不符合题意;
B、∵∠A=∠B,∠C=∠D,不符合“两组对角分别相等的四边形是平行四边形”,
∴不能判定四边形ABCD是平行四边形,故本选项不符合题意;
C、∵AB=AD,CB=CD,不符合“两组对边分别相等的四边形是平行四边形”,
∴不能判定四边形ABCD是平行四边形,故本选项不符合题意;
D、∵AB=CD,AD=BC,符合“两组对边分别相等的四边形是平行四边形”,
∴四边形ABCD是平行四边形,故本选项符合题意,
故选:D.
9.(2021春 雁塔区校级月考)如图,四边形ABCD的对角线AC、BD交于点O,下列条件:①∠BAD=∠BCD,∠ABC=∠ADC;②∠ABC=∠ADC,AB∥CD;③AB∥CD,OB=OD;④AB=CD,OA=OC,能判定四边形ABCD为平行四边形的有( )
A.1个 B.2个 C.3个 D.4个
【解析】解:①∵∠BAD=∠BCD,∠ABC=∠ADC,
∴四边形ABCD是平行四边形;
②∵AB∥CD,
∴∠ABC+∠BCD=180°,
∵∠ABC=∠ADC,
∴∠ADC+∠BCD=180°,
∴AD∥BC,
∴四边形ABCD是平行四边形;
③∵AB∥CD,
∴∠OAB=∠OCD,
在△AOB和△OCD中,
,
∴△AOB≌△OCD(AAS),
∴OA=OC,
∵OB=OD,
∴四边形ABCD是平行四边形;
④AB=CD,OA=OC,∠AOB=∠OCD,不能判定△AOB与△OCD全等,
∴不能判定四边形ABCD是平行四边形;
能判定四边形ABCD为平行四边形的有3个,
故选:C.
10.(2021春 邗江区校级期中)如图,在Rt△ABC中,∠B=90°,AB=3,AC=5,点D在BC上,以AC为对角线的所有 ADCE中,DE最小的值是( )
A.3 B.4 C.2 D.1
【解析】解:∵在Rt△ABC中,∠B=90°,
∴BC⊥AB.
∵四边形ADCE是平行四边形,
∴OD=OE,OA=OC.
∴当OD取最小值时,DE线段最短,此时OD⊥BC.
∴OD∥AB.
∵BD∥AE,
∴四边形ABDE是平行四边形,
∴DE=AB=3,
故选:A.
二.填空题
11.(2021春 雁塔区校级月考)已知平面直角坐标系内有四个点A(0,3),B(0,﹣1),C(3,4),D(3,y).若以点A,B,C,D为顶点的四边形是平行四边形,则y的值为 0或8 .
【解析】解:如图所示:
∵点A(0,3),B(0,﹣1),C(3,4),D(3,y),
∴AB∥CD,
由图象可知,满足条件的等D坐标为(3,0)或(3,8),
∴y=0或8,
故答案为:0或8.
12.(2021春 西湖区校级期中)如图,在 ABCD中,AC,BD相交于点O,点E,F在对角线BD上,有下列条件:①BF=DE;②AE=CF;③∠EAB=∠FCD;④AF∥CE.其中一定能判定四边形AECF是平行四边形的是 ①③④ .
【解析】解:①∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD,OB=OD,OA=OC,
∵BF=DE,
∴BF﹣OB=DE﹣OD,
即OF=OE,
∴四边形AECF是平行四边形;
③∵AB∥CD,
∴∠ABE=∠CDF,
∵∠BAE=∠DCF,
在△ABE和△CDF中,
,
∴△ABE≌△CDF(ASA),
∴BE=DF,
∵AO=CO,BO=DO,
∴OE=OF,
∴四边形AECF是平行四边形;
④∵AF∥CE,
∴∠AFB=∠CED,
在△ABF和△CDE中,
,
∴△ABF≌△CDE(AAS),
∴BF=DE,
∴BF﹣OB=DE﹣OD,
即OF=OE,
又∵OA=OC,
∴四边形AECF是平行四边形;
②∵AE=CF,不能判定△ABE≌△CDF,
∴不能判定四边形AECF是平行四边形;
∴一定能判定四边形AECF是平行四边形的是①③④,
故答案为:①③④.
13.(2021春 商河县校级期末)如图, ABCD中,点E在CD的延长线上,AE∥BD,EC=4,则AB的长是 2 .
【解析】解:如图,在 ABCD中,AB∥CD,且AB=CD.
∵点E在CD的延长线上,
∴AB∥ED.
又∵AE∥BD,
∴四边形ABDE是平行四边形,
∴AB=ED,
∴AB=ED=DC=EC=2.
故答案为:2.
14.(2021春 娄底期末)如图,在平行四边形ABCD中,E,F两点均在对角线AC上.要使四边形BEDF为平行四边形,在不添加辅助线的情况下,需要增加的一个条件是 AE=CF(答案不唯一) (写出一个即可).
【解析】解:增加条件:AE=CF,理由如下:
如图,连接BD交AC于点O,
∵四边形ABCD为平行四边形,
∴OB=OD,OA=OC,
若AE=CF,则有AO﹣AE=CO﹣CF,即OE=OF,
∴四边形BEDF为平行四边形,
故答案为:AE=CF(答案不唯一).
15.(2021秋 栖霞市期末)在△ABC中,∠C=90°,AC=6,BC=8,若以A,B,C,D为顶点的四边形是平行四边形,则此平行四边形的周长为 36或32或28 .
【解析】解:在△ABC中,∠C=90°,AC=6,BC=8,
∴AB===10,
如图1,平行四边形ABCD以AB、BC为邻边,
∵CD=AB=10,AD=BC=8,
∴10×2+8×2=36,
∴平行四边形ABCD的周长为36;
如图2,平行四边形ABDC以AB、AC为邻边,
∵CD=AB=10,DB=AC=6,
∴10×2+6×2=32,
∴平行四边形ABDC的周长为32;
如图3,平行四边形ACBD以AC、BC为邻边,
∵AD=BC=8,DB=AC=6,
∴8×2+6×2=28,
∴平行四边形ACBD的周长为28,
综上所述,此平行四边形的周长为36或32或28,
故答案为:36或32或28.
16.(2021春 路南区期中)如图,在四边形ABCD中,AB∥DC,AD=BC=6,DC=9,AB=15,点P从点A出发以2个单位/s的速度沿AD→DC向终点C运动,同时点Q从点B出发,以1个单位/s的速度沿BA向终点A运动.当有一点到达终点时,点P、Q就停止运动.当运动时间为 5 s时,四边形PQBC为平行四边形.
【解析】解:∵AD=BC=6,DC=9,
∴AD+DC=15,
由题意,点P在CD上,设运动时间为t秒,则CP=15﹣2t,BQ=t,
根据题意得到15﹣2t=t,
解得:t=5,
故答案为:5.
三.解答题
17.(2021秋 龙岗区校级期末)已知:如图,在平行四边形ABCD中,E,F分别是AB,CD的中点.
求证:(1)△AFD≌△CEB;
(2)四边形AECF是平行四边形.
【解析】证明:(1)∵四边形ABCD是平行四边形,
∴AB=CD,AD=BC,∠B=∠D,
又∵E,F分别是AB,CD的中点,
∴AE=BE=AB,CF=DF=CD,
∴BE=DF,AE=CF,
在△AFD和△CEB中,
,
∴△AFD≌△CEB(SAS);
(2)由(1)知AE=CF,△AFD≌△CEB,
∴AF=CE,
∴四边形AECF是平行四边形.
18.(2021 道外区三模)如图,在平行四边形ABCD中.点E在AD边上,点F在BC边上,且AE=CF,连接AF、BE相交于点M,连接CE、DF相交于点.
(1)如图1,求证:四边形EMFN为平行四边形;
(2)如图2,连接MN,若E是AD的中点,在不添加任何辅助线的情况下,请直接写出图2中以MN为边的所有平行四边形.
【解析】(1)证明:∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC,
∵AE=CF,
∴DE=BF,
∴四边形AECF和四边形DEBF都是平行四边形,
∴AF∥CE,BE∥DF,
∴四边形EMFN是平行四边形;
(2)解:以MN为边的所有平行四边形为:平行四边形BMNF、平行四边形EMND、平行四边形AMNE、平行四边形FMNC,理由如下:
连接EF,如图所示:
∵E是AD的中点,
∴AE=DE,
同(1)得:四边形ABFE、四边形CDEF、四边形AECF和四边形DEBF都是平行四边形,
∴AM=FM=AF,BM=EM=BE,EN=CN=CE,FN=DN=DF,AF∥CE,AF=CE,BE∥DF,BE=DF,
∴AM=EN=FM=CN,BM=FN=DN=EM,
∴四边形AMNE、四边形FMNC、四边形BMNF、四边形EMND是平行四边形,
19.(2022春 九龙坡区校级月考)在四边形ABCD中,AC、BD交于点O,AD∥BC,BO=DO.
(1)证明:四边形ABCD是平行四边形;
(2)过点O作OE⊥BD交BC于点E,连接DE.若∠CDE=∠CBD=15°,求∠ABC的度数.
【解析】(1)证明:∵AD∥BC,
∴∠ADO=∠CBO,
又∵∠AOD=∠BOC,OB=OD,
∴△AOD≌△COB(ASA),
∴AD=BC,
∴四边形ABCD是平行四边形;
(2)解:∵OB=OD,OE⊥BD,
∴BE=ED,
∴∠CBD=∠BDE=15°,
∵∠CDE=15°,
∴∠BDC=30°,
∵四边形ABCD是平行四边形,
∴AB∥CD,
∴∠ABD=∠BDC=30°,
∴∠ABC=∠ABD+∠CBD=30°+15°=45°.
20.(2022春 泰州月考)如图所示,△ABC≌△EAD,点E在BC上.
(1)求证:四边形ABCD是平行四边形;
(2)若∠B:∠CAD=5:4,AE⊥ED,求∠EDC的度数.
【解析】(1)证明:∵△ABC≌△EAD,
∴AD=BC,AB=AE,∠B=∠DAE,
∴∠B=∠AEB,
∴∠DAE=∠AEB,
∴AD∥BC,
∴四边形ABCD是平行四边形;
(2)解:由(1)知AD∥BC,
∴∠CAD=∠ACB,
∵∠B:∠CAD=5:4,
∴∠B:∠ACB=5:4,
设∠B=5x,∠ACB=4x,
∵AE⊥ED,
∴∠AED=90°,
∵△ABC≌△EAD,
∴∠BAC=∠AED=90°,
∴∠B+∠ACB=90°,
∴5x+4x=90°,
∴x=10°,
∴∠B=∠ADC=50°,∠ADE=∠ACB=4x=40°,
∴∠EDC=10°.
21.(2021 香坊区三模)如图1,在△ABC中,D是AB边上任意一点,E是BC边中点,过点C作AB的平行线,交DE的延长线于点F,连接BF,CD.
(1)求证:四边形CDBF是平行四边形;
(2)如图2,若∠FDB=30°,∠ABC=45°,BC=4,求DF的长.
【解析】(1)证明:∵CF∥AB,
∴∠ECF=∠EBD.
∵E是BC中点,
∴CE=BE.
∵∠CEF=∠BED,
∴△CEF≌△BED(ASA).
∴CF=BD.
∴四边形CDBF是平行四边形.
(2)解:如图,作EM⊥DB于点M,
∵四边形CDBF是平行四边形,BC=4,
∴BE=BC=2,DF=2DE.
在Rt△EMB中,EM=BE sin∠ABC=2,
在Rt△EMD中,∠EDM=30°,
∴DE=2EM=4,
∴DF=2DE=8.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
浙教版八年级下 4.4平行四边形的判定定理同步练习
一.选择题
1.(2021春 麦积区期末)在四边形ABCD中,AB∥CD,再添加下列其中一个条件后,四边形ABCD不一定是平行四边形的是( )
A.AB=CD B.AD=BC C.AD∥BC D.∠A=∠C
2.(2021春 娄星区校级期中)下列条件中,不能判定一个四边形为平行四边形的是( )
A.一组对边相等且平行 B.一组对边平行,另一组对边相等
C.两条对角线互相平分 D.两组对边分别相等
3.(2022 天河区一模)如图, ABCD中,E,F分别在边BC,AD上,添加选项中的条件后不能判定四边形AECF是平行四边形的是( )
A.BE=DF B.AE∥CF C.AF=EC D.AE=EC
4.(2022春 金华月考)如图,四边形ABCD的对角线AC,BD交于点O,则不能判断四边形ABCD是平行四边形的是( )
A.OB=OD,OA=OC B.AD∥BC,AB=CD
C.AB∥CD,AD∥BC D.AB∥CD,AB=CD
5.(2021秋 招远市期末)如图,在四边形ABCD中,AB∥CD,BC∥AD,且AD=DC,则下列说法:
①四边形ABCD是平行四边形; ②AB=BC;③AC⊥BD ④AC平分∠BAD;
⑤若AC=6,BD=8,则四边形ABCD的面积为24.
其中正确的有( )
A.2个 B.3个 C.4个 D.5个
6.(2012春 浦东新区期末)如图,已知四边形ABCD的面积为8cm2,AB∥CD,AB=CD,E是AB的中点,那么△AEC的面积是( )
A.4cm2 B.3cm2 C.2cm2 D.1cm2
7.(2021 霍邱县一模)如图,E是平行四边形ABCD的边AD的延长线上一点,连接BE交CD于点F,连接CE,BD.添加以下条件,仍不能判定四边形BCED为平行四边形的是( )
A.∠ABD=∠DCE B.∠AEC=∠CBD C.EF=BF D.∠AEB=∠BCD
8.(2021春 郧西县期末)下列能够判定四边形ABCD为平行四边形的条件是( )
A.AB∥CD,AD=BC B.∠A=∠B,∠C=∠D
C.AB=AD,CB=CD D.AB=CD,AD=BC
9.(2021春 雁塔区校级月考)如图,四边形ABCD的对角线AC、BD交于点O,下列条件:①∠BAD=∠BCD,∠ABC=∠ADC;②∠ABC=∠ADC,AB∥CD;③AB∥CD,OB=OD;④AB=CD,OA=OC,能判定四边形ABCD为平行四边形的有( )
A.1个 B.2个 C.3个 D.4个
10.(2021春 邗江区校级期中)如图,在Rt△ABC中,∠B=90°,AB=3,AC=5,点D在BC上,以AC为对角线的所有 ADCE中,DE最小的值是( )
A.3 B.4 C.2 D.1
二.填空题
11.(2021春 雁塔区校级月考)已知平面直角坐标系内有四个点A(0,3),B(0,﹣1),C(3,4),D(3,y).若以点A,B,C,D为顶点的四边形是平行四边形,则y的值为 .
12.(2021春 西湖区校级期中)如图,在 ABCD中,AC,BD相交于点O,点E,F在对角线BD上,有下列条件:①BF=DE;②AE=CF;③∠EAB=∠FCD;④AF∥CE.其中一定能判定四边形AECF是平行四边形的是 .
13.(2021春 商河县校级期末)如图, ABCD中,点E在CD的延长线上,AE∥BD,EC=4,则AB的长是 .
14.(2021春 娄底期末)如图,在平行四边形ABCD中,E,F两点均在对角线AC上.要使四边形BEDF为平行四边形,在不添加辅助线的情况下,需要增加的一个条件是 (写出一个即可).
15.(2021秋 栖霞市期末)在△ABC中,∠C=90°,AC=6,BC=8,若以A,B,C,D为顶点的四边形是平行四边形,则此平行四边形的周长为 .
16.(2021春 路南区期中)如图,在四边形ABCD中,AB∥DC,AD=BC=6,DC=9,AB=15,点P从点A出发以2个单位/s的速度沿AD→DC向终点C运动,同时点Q从点B出发,以1个单位/s的速度沿BA向终点A运动.当有一点到达终点时,点P、Q就停止运动.当运动时间为 s时,四边形PQBC为平行四边形.
三.解答题
17.(2021秋 龙岗区校级期末)已知:如图,在平行四边形ABCD中,E,F分别是AB,CD的中点.
求证:(1)△AFD≌△CEB;
(2)四边形AECF是平行四边形.
18.(2021 道外区三模)如图,在平行四边形ABCD中.点E在AD边上,点F在BC边上,且AE=CF,连接AF、BE相交于点M,连接CE、DF相交于点.
(1)如图1,求证:四边形EMFN为平行四边形;
(2)如图2,连接MN,若E是AD的中点,在不添加任何辅助线的情况下,请直接写出图2中以MN为边的所有平行四边形.
19.(2022春 九龙坡区校级月考)在四边形ABCD中,AC、BD交于点O,AD∥BC,BO=DO.
(1)证明:四边形ABCD是平行四边形;
(2)过点O作OE⊥BD交BC于点E,连接DE.若∠CDE=∠CBD=15°,求∠ABC的度数.
20.(2022春 泰州月考)如图所示,△ABC≌△EAD,点E在BC上.
(1)求证:四边形ABCD是平行四边形;
(2)若∠B:∠CAD=5:4,AE⊥ED,求∠EDC的度数.
21.(2021 香坊区三模)如图1,在△ABC中,D是AB边上任意一点,E是BC边中点,过点C作AB的平行线,交DE的延长线于点F,连接BF,CD.
(1)求证:四边形CDBF是平行四边形;
(2)如图2,若∠FDB=30°,∠ABC=45°,BC=4,求DF的长.
答案与解析
一.选择题
1.(2021春 麦积区期末)在四边形ABCD中,AB∥CD,再添加下列其中一个条件后,四边形ABCD不一定是平行四边形的是( )
A.AB=CD B.AD=BC C.AD∥BC D.∠A=∠C
【解析】解:A、∵AB∥CD,若AB=CD,则四边形ABCD是平行四边形,故A选项不符合题意;
B、∵AB∥CD,若AD=BC,则四边形ABCD可能是等腰梯形,不一定是平行四边形,故B选项符合题意;
C、∵AB∥CD,若AD∥BC,则四边形ABCD是平行四边形,故C选项不符合题意;
D、∵AB∥CD,若∠A=∠C,则四边形ABCD是平行四边形,故D选项不符合题意;
故选:B.
2.(2021春 娄星区校级期中)下列条件中,不能判定一个四边形为平行四边形的是( )
A.一组对边相等且平行 B.一组对边平行,另一组对边相等
C.两条对角线互相平分 D.两组对边分别相等
【解析】解:A、一组对边相等且平行的四边形是平行四边形,故本选项不符合题意;
B、一组对边平行且另一组对边相等的四边形不一定是平行四边形,可能是等腰梯形,故本选项符合题意;
C、两条对角线互相平分是平行四边形,故本选项不符合题意;
D、两组对边分别相等的四边形是平行四边形,故本选项不符合题意;
故选:B.
3.(2022 天河区一模)如图, ABCD中,E,F分别在边BC,AD上,添加选项中的条件后不能判定四边形AECF是平行四边形的是( )
A.BE=DF B.AE∥CF C.AF=EC D.AE=EC
【解析】解:A、∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC,
∵BE=DF,
∴AF=CE,
∴四边形AECF是平行四边形,故选项A不符合题意;
B、∵四边形ABCD是平行四边形,
∴AD∥BC,
∵AE∥CF,
∴四边形AECF是平行四边形,故选项B不符合题意;
C、∵四边形ABCD是平行四边形,
∴AD∥BC,
∵AF=EC,
∴四边形AECF是平行四边形,故选项C不符合题意;
D、∵四边形ABCD是平行四边形,
∴AD∥BC,
由AE=EC,不能判定四边形AECF是平行四边形,故选项D符合题意;
故选:D.
4.(2022春 金华月考)如图,四边形ABCD的对角线AC,BD交于点O,则不能判断四边形ABCD是平行四边形的是( )
A.OB=OD,OA=OC B.AD∥BC,AB=CD
C.AB∥CD,AD∥BC D.AB∥CD,AB=CD
【解析】解:A、∵OB=OD,OA=OC,∴四边形ABCD是平行四边形,故此选项不合题意;
B、∵AD∥BC,AB=CD,不能判断四边形ABCD是平行四边形,故此选项符合题意;
C、∵AB∥CD,AD∥BC,∴四边形ABCD是平行四边形,故此选项不合题意;
D、∵AB∥CD,AB=CD,∴四边形ABCD是平行四边形,故此选项不合题意;
故选:B.
5.(2021秋 招远市期末)如图,在四边形ABCD中,AB∥CD,BC∥AD,且AD=DC,则下列说法:
①四边形ABCD是平行四边形; ②AB=BC; ③AC⊥BD ④AC平分∠BAD;
⑤若AC=6,BD=8,则四边形ABCD的面积为24.
其中正确的有( )
A.2个 B.3个 C.4个 D.5个
【解析】解:∵AB∥CD,BC∥AD,
∴四边形ABCD是平行四边形,故①正确;
∵AD=DC,
∴平行四边形ABCD是菱形,
∴AB=BC,AC⊥BD,AC平分∠BAD,故②③④正确,
∵AC=6,BD=8,
∴菱形ABCD的面积=AC×BD=×6×8=24,故⑤正确;
正确的个数有5个,
故选:D.
6.(2012春 浦东新区期末)如图,已知四边形ABCD的面积为8cm2,AB∥CD,AB=CD,E是AB的中点,那么△AEC的面积是( )
A.4cm2 B.3cm2 C.2cm2 D.1cm2
【解析】解:∵AB∥CD,AB=CD,
∴四边形ABCD是平行四边形,
∴S△ADC=S△ABC=×8=4,
∵E是AB的中点,
∴S△AEC=S△ABC=×4=2cm2,
故选:C.
7.(2021 霍邱县一模)如图,E是平行四边形ABCD的边AD的延长线上一点,连接BE交CD于点F,连接CE,BD.添加以下条件,仍不能判定四边形BCED为平行四边形的是( )
A.∠ABD=∠DCE B.∠AEC=∠CBD C.EF=BF D.∠AEB=∠BCD
【解析】解:A、∵四边形ABCD是平行四边形,
∴AD∥BC,AB∥CD,
∴DE∥BC,∠ABD=∠CDB,
∵∠ABD=∠DCE,
∴∠DCE=∠CDB,
∴BD∥CE,
∴四边形BCED为平行四边形,故A不符合题意;
B、∵AE∥BC,
∴∠DEC+∠BCE=∠EDB+∠DBC=180°,
∵∠AEC=∠CBD,
∴∠BDE=∠BCE,
∴四边形BCED为平行四边形,故B不符合题意,
C、∵DE∥BC,
∴∠DEF=∠CBF,
在△DEF与△CBF中,
,
∴△DEF≌△CBF(ASA),
∴DF=CF,
∵EF=BF,
∴四边形BCED为平行四边形,故C不符合题意;
D、∵AE∥BC,
∴∠AEB=∠CBF,
∵∠AEB=∠BCD,
∴∠CBF=∠BCD,
∴CF=BF,
同理,EF=DF,
∴不能判定四边形BCED为平行四边形;故D符合题意;
故选:D.
8.(2021春 郧西县期末)下列能够判定四边形ABCD为平行四边形的条件是( )
A.AB∥CD,AD=BC B.∠A=∠B,∠C=∠D
C.AB=AD,CB=CD D.AB=CD,AD=BC
【解析】解:如图所示:
A、∵AB∥CD,AD=BC,不符合“一组对边平行且相等的四边形是平行四边形”,
∴不能判定四边形ABCD是平行四边形,故本选项不符合题意;
B、∵∠A=∠B,∠C=∠D,不符合“两组对角分别相等的四边形是平行四边形”,
∴不能判定四边形ABCD是平行四边形,故本选项不符合题意;
C、∵AB=AD,CB=CD,不符合“两组对边分别相等的四边形是平行四边形”,
∴不能判定四边形ABCD是平行四边形,故本选项不符合题意;
D、∵AB=CD,AD=BC,符合“两组对边分别相等的四边形是平行四边形”,
∴四边形ABCD是平行四边形,故本选项符合题意,
故选:D.
9.(2021春 雁塔区校级月考)如图,四边形ABCD的对角线AC、BD交于点O,下列条件:①∠BAD=∠BCD,∠ABC=∠ADC;②∠ABC=∠ADC,AB∥CD;③AB∥CD,OB=OD;④AB=CD,OA=OC,能判定四边形ABCD为平行四边形的有( )
A.1个 B.2个 C.3个 D.4个
【解析】解:①∵∠BAD=∠BCD,∠ABC=∠ADC,
∴四边形ABCD是平行四边形;
②∵AB∥CD,
∴∠ABC+∠BCD=180°,
∵∠ABC=∠ADC,
∴∠ADC+∠BCD=180°,
∴AD∥BC,
∴四边形ABCD是平行四边形;
③∵AB∥CD,
∴∠OAB=∠OCD,
在△AOB和△OCD中,
,
∴△AOB≌△OCD(AAS),
∴OA=OC,
∵OB=OD,
∴四边形ABCD是平行四边形;
④AB=CD,OA=OC,∠AOB=∠OCD,不能判定△AOB与△OCD全等,
∴不能判定四边形ABCD是平行四边形;
能判定四边形ABCD为平行四边形的有3个,
故选:C.
10.(2021春 邗江区校级期中)如图,在Rt△ABC中,∠B=90°,AB=3,AC=5,点D在BC上,以AC为对角线的所有 ADCE中,DE最小的值是( )
A.3 B.4 C.2 D.1
【解析】解:∵在Rt△ABC中,∠B=90°,
∴BC⊥AB.
∵四边形ADCE是平行四边形,
∴OD=OE,OA=OC.
∴当OD取最小值时,DE线段最短,此时OD⊥BC.
∴OD∥AB.
∵BD∥AE,
∴四边形ABDE是平行四边形,
∴DE=AB=3,
故选:A.
二.填空题
11.(2021春 雁塔区校级月考)已知平面直角坐标系内有四个点A(0,3),B(0,﹣1),C(3,4),D(3,y).若以点A,B,C,D为顶点的四边形是平行四边形,则y的值为 0或8 .
【解析】解:如图所示:
∵点A(0,3),B(0,﹣1),C(3,4),D(3,y),
∴AB∥CD,
由图象可知,满足条件的等D坐标为(3,0)或(3,8),
∴y=0或8,
故答案为:0或8.
12.(2021春 西湖区校级期中)如图,在 ABCD中,AC,BD相交于点O,点E,F在对角线BD上,有下列条件:①BF=DE;②AE=CF;③∠EAB=∠FCD;④AF∥CE.其中一定能判定四边形AECF是平行四边形的是 ①③④ .
【解析】解:①∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD,OB=OD,OA=OC,
∵BF=DE,
∴BF﹣OB=DE﹣OD,
即OF=OE,
∴四边形AECF是平行四边形;
③∵AB∥CD,
∴∠ABE=∠CDF,
∵∠BAE=∠DCF,
在△ABE和△CDF中,
,
∴△ABE≌△CDF(ASA),
∴BE=DF,
∵AO=CO,BO=DO,
∴OE=OF,
∴四边形AECF是平行四边形;
④∵AF∥CE,
∴∠AFB=∠CED,
在△ABF和△CDE中,
,
∴△ABF≌△CDE(AAS),
∴BF=DE,
∴BF﹣OB=DE﹣OD,
即OF=OE,
又∵OA=OC,
∴四边形AECF是平行四边形;
②∵AE=CF,不能判定△ABE≌△CDF,
∴不能判定四边形AECF是平行四边形;
∴一定能判定四边形AECF是平行四边形的是①③④,
故答案为:①③④.
13.(2021春 商河县校级期末)如图, ABCD中,点E在CD的延长线上,AE∥BD,EC=4,则AB的长是 2 .
【解析】解:如图,在 ABCD中,AB∥CD,且AB=CD.
∵点E在CD的延长线上,
∴AB∥ED.
又∵AE∥BD,
∴四边形ABDE是平行四边形,
∴AB=ED,
∴AB=ED=DC=EC=2.
故答案为:2.
14.(2021春 娄底期末)如图,在平行四边形ABCD中,E,F两点均在对角线AC上.要使四边形BEDF为平行四边形,在不添加辅助线的情况下,需要增加的一个条件是 AE=CF(答案不唯一) (写出一个即可).
【解析】解:增加条件:AE=CF,理由如下:
如图,连接BD交AC于点O,
∵四边形ABCD为平行四边形,
∴OB=OD,OA=OC,
若AE=CF,则有AO﹣AE=CO﹣CF,即OE=OF,
∴四边形BEDF为平行四边形,
故答案为:AE=CF(答案不唯一).
15.(2021秋 栖霞市期末)在△ABC中,∠C=90°,AC=6,BC=8,若以A,B,C,D为顶点的四边形是平行四边形,则此平行四边形的周长为 36或32或28 .
【解析】解:在△ABC中,∠C=90°,AC=6,BC=8,
∴AB===10,
如图1,平行四边形ABCD以AB、BC为邻边,
∵CD=AB=10,AD=BC=8,
∴10×2+8×2=36,
∴平行四边形ABCD的周长为36;
如图2,平行四边形ABDC以AB、AC为邻边,
∵CD=AB=10,DB=AC=6,
∴10×2+6×2=32,
∴平行四边形ABDC的周长为32;
如图3,平行四边形ACBD以AC、BC为邻边,
∵AD=BC=8,DB=AC=6,
∴8×2+6×2=28,
∴平行四边形ACBD的周长为28,
综上所述,此平行四边形的周长为36或32或28,
故答案为:36或32或28.
16.(2021春 路南区期中)如图,在四边形ABCD中,AB∥DC,AD=BC=6,DC=9,AB=15,点P从点A出发以2个单位/s的速度沿AD→DC向终点C运动,同时点Q从点B出发,以1个单位/s的速度沿BA向终点A运动.当有一点到达终点时,点P、Q就停止运动.当运动时间为 5 s时,四边形PQBC为平行四边形.
【解析】解:∵AD=BC=6,DC=9,
∴AD+DC=15,
由题意,点P在CD上,设运动时间为t秒,则CP=15﹣2t,BQ=t,
根据题意得到15﹣2t=t,
解得:t=5,
故答案为:5.
三.解答题
17.(2021秋 龙岗区校级期末)已知:如图,在平行四边形ABCD中,E,F分别是AB,CD的中点.
求证:(1)△AFD≌△CEB;
(2)四边形AECF是平行四边形.
【解析】证明:(1)∵四边形ABCD是平行四边形,
∴AB=CD,AD=BC,∠B=∠D,
又∵E,F分别是AB,CD的中点,
∴AE=BE=AB,CF=DF=CD,
∴BE=DF,AE=CF,
在△AFD和△CEB中,
,
∴△AFD≌△CEB(SAS);
(2)由(1)知AE=CF,△AFD≌△CEB,
∴AF=CE,
∴四边形AECF是平行四边形.
18.(2021 道外区三模)如图,在平行四边形ABCD中.点E在AD边上,点F在BC边上,且AE=CF,连接AF、BE相交于点M,连接CE、DF相交于点.
(1)如图1,求证:四边形EMFN为平行四边形;
(2)如图2,连接MN,若E是AD的中点,在不添加任何辅助线的情况下,请直接写出图2中以MN为边的所有平行四边形.
【解析】(1)证明:∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC,
∵AE=CF,
∴DE=BF,
∴四边形AECF和四边形DEBF都是平行四边形,
∴AF∥CE,BE∥DF,
∴四边形EMFN是平行四边形;
(2)解:以MN为边的所有平行四边形为:平行四边形BMNF、平行四边形EMND、平行四边形AMNE、平行四边形FMNC,理由如下:
连接EF,如图所示:
∵E是AD的中点,
∴AE=DE,
同(1)得:四边形ABFE、四边形CDEF、四边形AECF和四边形DEBF都是平行四边形,
∴AM=FM=AF,BM=EM=BE,EN=CN=CE,FN=DN=DF,AF∥CE,AF=CE,BE∥DF,BE=DF,
∴AM=EN=FM=CN,BM=FN=DN=EM,
∴四边形AMNE、四边形FMNC、四边形BMNF、四边形EMND是平行四边形,
19.(2022春 九龙坡区校级月考)在四边形ABCD中,AC、BD交于点O,AD∥BC,BO=DO.
(1)证明:四边形ABCD是平行四边形;
(2)过点O作OE⊥BD交BC于点E,连接DE.若∠CDE=∠CBD=15°,求∠ABC的度数.
【解析】(1)证明:∵AD∥BC,
∴∠ADO=∠CBO,
又∵∠AOD=∠BOC,OB=OD,
∴△AOD≌△COB(ASA),
∴AD=BC,
∴四边形ABCD是平行四边形;
(2)解:∵OB=OD,OE⊥BD,
∴BE=ED,
∴∠CBD=∠BDE=15°,
∵∠CDE=15°,
∴∠BDC=30°,
∵四边形ABCD是平行四边形,
∴AB∥CD,
∴∠ABD=∠BDC=30°,
∴∠ABC=∠ABD+∠CBD=30°+15°=45°.
20.(2022春 泰州月考)如图所示,△ABC≌△EAD,点E在BC上.
(1)求证:四边形ABCD是平行四边形;
(2)若∠B:∠CAD=5:4,AE⊥ED,求∠EDC的度数.
【解析】(1)证明:∵△ABC≌△EAD,
∴AD=BC,AB=AE,∠B=∠DAE,
∴∠B=∠AEB,
∴∠DAE=∠AEB,
∴AD∥BC,
∴四边形ABCD是平行四边形;
(2)解:由(1)知AD∥BC,
∴∠CAD=∠ACB,
∵∠B:∠CAD=5:4,
∴∠B:∠ACB=5:4,
设∠B=5x,∠ACB=4x,
∵AE⊥ED,
∴∠AED=90°,
∵△ABC≌△EAD,
∴∠BAC=∠AED=90°,
∴∠B+∠ACB=90°,
∴5x+4x=90°,
∴x=10°,
∴∠B=∠ADC=50°,∠ADE=∠ACB=4x=40°,
∴∠EDC=10°.
21.(2021 香坊区三模)如图1,在△ABC中,D是AB边上任意一点,E是BC边中点,过点C作AB的平行线,交DE的延长线于点F,连接BF,CD.
(1)求证:四边形CDBF是平行四边形;
(2)如图2,若∠FDB=30°,∠ABC=45°,BC=4,求DF的长.
【解析】(1)证明:∵CF∥AB,
∴∠ECF=∠EBD.
∵E是BC中点,
∴CE=BE.
∵∠CEF=∠BED,
∴△CEF≌△BED(ASA).
∴CF=BD.
∴四边形CDBF是平行四边形.
(2)解:如图,作EM⊥DB于点M,
∵四边形CDBF是平行四边形,BC=4,
∴BE=BC=2,DF=2DE.
在Rt△EMB中,EM=BE sin∠ABC=2,
在Rt△EMD中,∠EDM=30°,
∴DE=2EM=4,
∴DF=2DE=8.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
- 第一章 二次根式
- 1.1 二次根式
- 1.2 二次根式的性质
- 1.3 二次根式的运算
- 第二章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程的应用
- 2.4 一元二次方程根与系数的关系(选学)
- 第三章 数据分析初步
- 3.1 平均数
- 3.2 中位数和众数
- 3.3 方差和标准差
- 第四章 平行四边形
- 4.1 多边形
- 4.2 平行四边形
- 4.3 中心对称
- 4.4 平行四边形的判定
- 4.5 三角形的中位线
- 4.6 反证法
- 第五章 特殊平行四边形
- 5.1 矩形
- 5.2 菱形
- 5.3 正方形
- 第六章 反比例函数
- 6.1 反比例函数
- 6.2 反比例函数的图象和性质
- 6.3 反比例函数的应用
