浙教A版九年级数学上册 第1章二次函数 达标检测卷(word版含答案)
文档属性
| 名称 | 浙教A版九年级数学上册 第1章二次函数 达标检测卷(word版含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 454.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-13 18:33:38 | ||
图片预览




文档简介
浙教A版九年级数学上册 第1章 达标检测卷
(限时: 120分钟 满分: 120分)
班级: 姓名: 得分:
一、单选题(每题3分,共30分)
1.下列函数中是二次函数的是( )
A.y=3x-1 B.y=3x2-1 C.y=(x+1)2-x2 D.y=
2.对于二次函数y=-(x-1)2+4的图象,下列说法正确的是( )
A.开口向上 B.对称轴是直线x=-1
C.与y轴交点的坐标是(0,4) D.在x轴上截得的线段长度是4
3.对于二次函数y=x2+bx+c,函数y与自变量x的部分对应值如下表:
x … -1 0 1 2 3 4 …
y … 10 5 2 1 2 5 …
该二次函数图象的对称轴是直线( )
A.x=0 B.x=1 C.x=2 D.x=3
4.二次函数y=ax2+bx+c(a≠0)的部分图象如图所示,它与x轴的一个交点坐标为(-3,0),当y>0时,则x的取值范围是( )
A.x<-3
B.x>1
C.-3<x<1
D.x<-3或x>1
5.飞机着陆后滑行的距离s(米)关于滑行的时间t(秒)的函数表达式是s=60t-1.5t2,则飞机着陆后从开始滑行到停止,滑行的距离为( )
A.500米 B.600米 C.700米 D.800米
6.将函数y=3x2的图象先向右平移2个单位,再向上平移5个单位,所得图象的函数表达式是( )
A.y=3(x-2)2-5
B.y=3(x-2)2+5
C.y=3(x+2)2-5
D.y=3(x+2)2+5
7.已知二次函数y=2mx2+(4-m)x,它的图象可能是( )
8.已知抛物线y=ax2+bx+c(a,b,c为常数且a≠0)经过P1(1,y1),P2(2,y2),P3(3,y3),P4(4,y4)四点,若y3<y2<y1,则下列说法中一定正确的是( )
A.抛物线开口向下 B.对称轴为直线x=3
C.y1>y4 D.5a+b>0
9.如图,抛物线y=ax2+bx+c与x轴交于点A(-1,0),顶点坐标为(1,n),与y轴的交点在(0,3),(0,4)之间(包含端点),则下列结论:①abc>0;②2a+b=0;③-≤a≤-1;④a+b≥am2+bm(m为任意实数);⑤方程|ax2+bx+c|=n有四个不相等的实数根.其中正确的有( )
A.2个
B.3个
C.4个
D.5个
10.如图,在菱形ABCD中,AB=2 cm,∠D=60°,点P,Q同时从点A出发,点P以1 cm/s的速度沿A→C→D的方向运动,点Q以2 cm/s的速度沿A→B→C→D的方向运动,当其中一点到达点D时,两点停止运动.设运动时间为x(s),△APQ的面积为y(cm2),则下列图象中能大致反映y关于x的函数关系的是( )
二、填空题(每题4分,共24分)
11.已知函数y=x2+2x+1,当y=0时,x=________;当112.如图,在平面直角坐标系xOy中,抛物线y=ax2+bx+c的对称轴为直线x=2,与x轴的一个交点为(1,0),则关于x的方程ax2+bx+c=0的解是________.
13.抛物线y=x2-3x+2与x轴的交点有________个.
14.如图,线段AB=8,点C是AB上一点,点D、E是线段AC的三等分点,分别以AD、DE、EC、CB为边作正方形,则AC=________时,四个正方形的面积之和最小.
15.对于二次函数y=x2-2mx-3,有下列说法:①它的图象与x轴有两个交点;②如果当x≤1时,y随x的增大而减小,则m=1;③若图象向左平移3个单位后过原点,则m=-1;④若当x=4时的函数值与当x=100时的函数值相等,则当x=104时的函数值为-3.其中正确说法的序号是________.
16.如图,抛物线y=x2+x-3与x轴交于A、B两点,与y轴交于点C,点D为抛物线上、第三象限内一动点,当∠ACD+2∠ABC=180°时,点D的坐标为________.
三、解答题(共66分)
17.(6分)在直角坐标系xOy中,二次函数y=x2+bx+c的图象过点A(1,0)和点B(0,-3).
(1)求此二次函数的表达式;
(2)设此二次函数图象的顶点为C,写出另一个过点C的二次函数的表达式.
18.(6分)已知二次函数y=-x2+2x+3.
(1)用描点法画出它的图象;
(2)该二次函数的顶点坐标是________,点P(2,3)________(填“在”或“不在”)该二次函数的图象上.
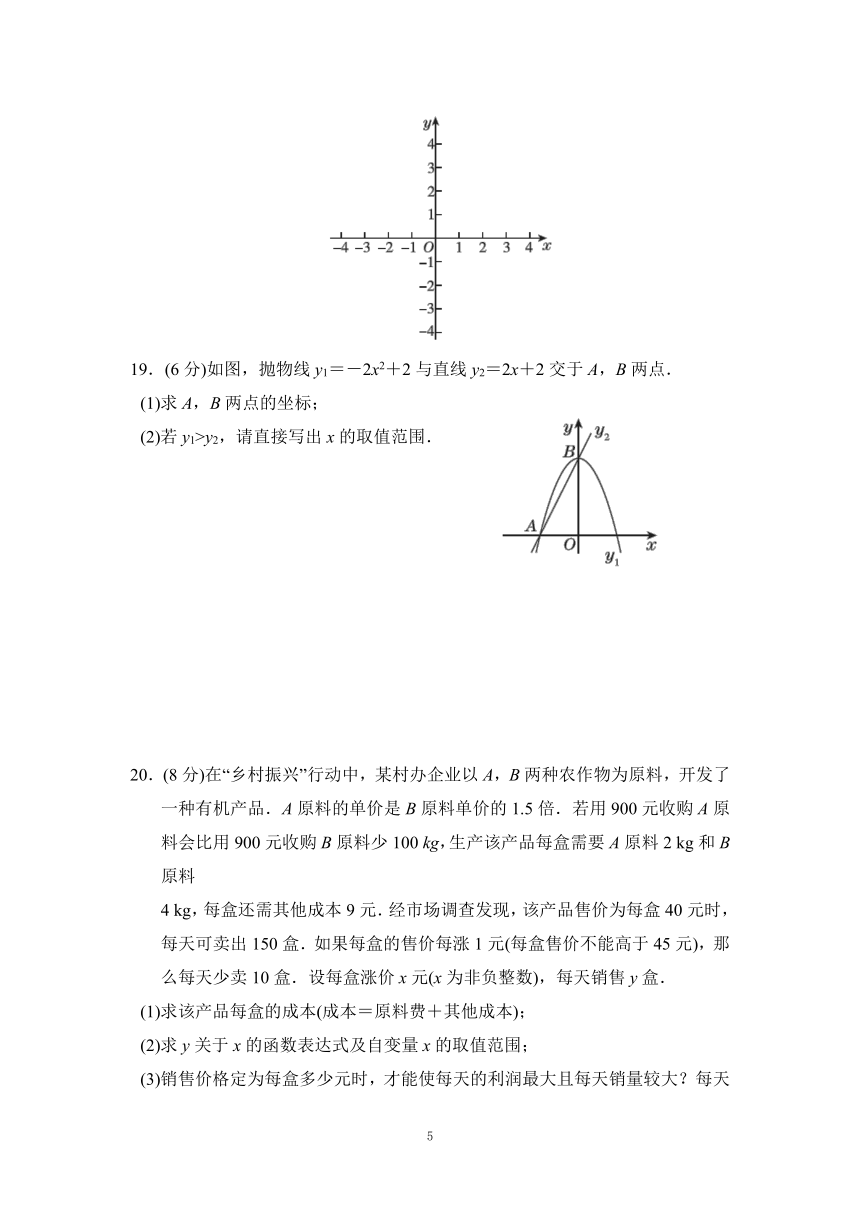
19.(6分)如图,抛物线y1=-2x2+2与直线y2=2x+2交于A,B两点.
(1)求A,B两点的坐标;
(2)若y1>y2,请直接写出x的取值范围.
20.(8分)在“乡村振兴”行动中,某村办企业以A,B两种农作物为原料,开发了一种有机产品.A原料的单价是B原料单价的1.5倍.若用900元收购A原料会比用900元收购B原料少100 kg,生产该产品每盒需要A原料2 kg和B原料
4 kg,每盒还需其他成本9元.经市场调查发现,该产品售价为每盒40元时,每天可卖出150盒.如果每盒的售价每涨1元(每盒售价不能高于45元),那么每天少卖10盒.设每盒涨价x元(x为非负整数),每天销售y盒.
(1)求该产品每盒的成本(成本=原料费+其他成本);
(2)求y关于x的函数表达式及自变量x的取值范围;
(3)销售价格定为每盒多少元时,才能使每天的利润最大且每天销量较大?每天的最大利润是多少元?
21.(8分)在平面直角坐标系xOy中,抛物线y=mx2-2mx-2m+1与x轴交于A,B两点.
(1)若AB=2,求m的值;
(2)过点P(0,2)作与x轴平行的直线,交抛物线于点M,N.当MN≥2时,求m的取值范围.
22.如图所示是隧道的截面,由抛物线和长方形构成,长方形的长是12 m,宽是
4 m.按照图中所示的直角坐标系,抛物线可以用y=-x2+bx+c表示,且抛物线上的点C到OB的水平距离为3 m,到地面OA的距离为 m.
(1)求抛物线的函数表达式,并计算出隧道顶点D到地面OA的距离;
(2)一辆货车载一长方体集装箱后高为6 m,宽为4 m,如果隧道内设双向车道,那么这辆货车能否安全通过?
(3)在隧道的抛物线形拱壁上需要安装两排灯,使它们离地面的高度相等,如果灯离地面的高度不超过8 m,那么两排灯的水平距离最小是多少米?
23.(10分)如图,在平面直角坐标系中,过原点的抛物线的顶点M的坐标为(-1,-1),点A的坐标为(1,1),以OA为边的菱形OABC的顶点C在x轴的正半轴上,把菱形OABC沿AB向上翻折得到菱形EABD.
(1)求抛物线对应的函数表达式;
(2)若把抛物线向右平移使抛物线经过点D,求平移的距离.
24.(12分)对于某一函数给出如下定义:如果存在实数p,当其自变量的值为p时,其函数值等于p,则称p为这个函数的不动值.在函数存在不动值时,该函数的最大不动值与最小不动值之差q称为这个函数的不动长度,特别地,当函数只有一个不动值时,其不动长度q为0.例如,下图中的函数有0和1两个不动值,其不动长度q为1.
(1)下列函数:①y=2x;②y=x2+1;③y=x2-2x.其中存在不动值的是________(填序号).
(2)函数y=3x2+bx,
①若其不动长度为0,则b的值为________.
②若-2≤b≤2,求其不动长度q的取值范围.
(3)记函数y=x2-4x(x≥m)的图象为G1,将G1沿x=m翻折后得到的函数图象记为G2,函数G的图象由G1和G2两部分组成,若其不动长度q满足0≤q≤5,则m的取值范围为________.
答案
一、1.B 2.D 3.C 4.D 5.B 6.B
7.B 8.C 9.B 10.A
二、11.-1;增大 12.x1=1,x2=3
13.2 14.6 15.①④ 16.
三、17.解:(1)把点A(1,0)的坐标和点B(0,-3)的坐标代入y=x2+bx+c,
得解得
∴此二次函数的表达式为y=x2+2x-3.
(2)y=x2+2x-3=(x+1)2-4,则此二次函数图象的顶点C的坐标为(-1,-4).
另一个过点C的二次函数的表达式为y=-(x+1)2-4(答案不唯一).
18.解:(1)列表:
x … -1 0 1 2 3 …
y … 0 3 4 3 0 …
描点,画图如下:
(2)(1,4);在
19.解:(1)由题可得
解得或
∴A,B两点的坐标分别是(-1,0),(0,2).
(2)由图可知,当y1>y2时,x的取值范围是-1<x<0.
20.解:(1)设B原料单价为每千克m元,则A原料单价为千克1.5m元,
根据题意,得-=100,
解得m=3.∴1.5m=1.5×3=4.5.
∴该产品每盒的成本为4.5×2+3×4+9=30(元).
答:该产品每盒的成本为30元.
(2)y关于x的函数表达式是y=150-10x(0≤x≤5,且x为整数).
(3)设每天的利润为w元,
则w=(40+x-30)(150-10x)
=-10x2+50x+1 500
=-102+(0≤x≤5,且x为整数),
∴当x=2或x=3时,w取得最大值,最大值为1 560.
又∵要求每天销量较大,∴x=2.
∴每盒定价为42元.
答:销售价格定为每盒42元时,才能使每天的利润最大且每天销量较大,每天的最大利润是1 560元.
21.解:(1)抛物线y=mx2-2mx-2m+1的对称轴为直线x=-=1.
∵点A,B关于直线x=1对称,AB=2,
∴抛物线与x轴交于点A(0,0),B(2,0).将A(0,0)的坐标代入y=mx2-2mx-2m+1中,得-2m+1=0,解得m=.
(2)∴抛物线y=mx2-2mx-2m+1与x轴有两个交点,
∴Δ>0,即(-2m)2-4m(-2m+1)>0,解得m>或m<0.
①若m>0,则抛物线开口向上.
当MN≥2时,有-2m+1≤2,
解得m≥-,∴m>;
②若m<0,则抛物线开口向下.
当MN≥2时,有-2m+1≥2,
解得m≤-,∴m≤-.
综上所述,m的取值范围为m>或m≤-.
22.解:(1)由题知点B(0,4),
C在抛物线上,
则有
解得
所以y=-x2+2x+4.
当x=-=6时,y=10.
即隧道顶点D到地面OA的距离为10 m.
(2)由题知货车最外侧与地面OA的交点为(2,0)或(10,0),
当x=2或x=10时,y=>6,
所以这辆货车能安全通过.
(3)令y=8,有-x2+2x+4=8,可得x2-12x+24=0,
解得x1=6+2 ,x2=6-2 ,
x1-x2=4 .
答:两排灯的水平距离最小是4 m.
23.解:(1)设抛物线对应的函数表达式为y=a(x+1)2-1,
把点O(0,0)的坐标代入,得a=1.
∴抛物线对应的函数表达式为y=(x+1)2-1.
(2)∵点A(1,1),∴OA=.
∵菱形EABD是由菱形OABC沿AB向上翻折得到,
∴OE=2,DE=OC=OA=.
∴点D的坐标为(,2).
设抛物线向右平移后得到的抛物线的函数表达式为y=(x+1-m)2-1.
由题意得(+1-m)2-1=2,
解得m1=+1+,m2=+1-.
∴平移的距离为+1+或+1-.
24.解:(1)①③
(2)① 1
②由题意得3x2+bx=x,解得x=0或x=.∴q=,
当-2≤b≤1时,q=,
此时0≤q≤1;
当1≤b≤2时,q=-,
此时0≤q≤.
综上,其不动长度q的取值范围为0≤q≤1.
(3)2≤m≤5或m<-.
PAGE
(限时: 120分钟 满分: 120分)
班级: 姓名: 得分:
一、单选题(每题3分,共30分)
1.下列函数中是二次函数的是( )
A.y=3x-1 B.y=3x2-1 C.y=(x+1)2-x2 D.y=
2.对于二次函数y=-(x-1)2+4的图象,下列说法正确的是( )
A.开口向上 B.对称轴是直线x=-1
C.与y轴交点的坐标是(0,4) D.在x轴上截得的线段长度是4
3.对于二次函数y=x2+bx+c,函数y与自变量x的部分对应值如下表:
x … -1 0 1 2 3 4 …
y … 10 5 2 1 2 5 …
该二次函数图象的对称轴是直线( )
A.x=0 B.x=1 C.x=2 D.x=3
4.二次函数y=ax2+bx+c(a≠0)的部分图象如图所示,它与x轴的一个交点坐标为(-3,0),当y>0时,则x的取值范围是( )
A.x<-3
B.x>1
C.-3<x<1
D.x<-3或x>1
5.飞机着陆后滑行的距离s(米)关于滑行的时间t(秒)的函数表达式是s=60t-1.5t2,则飞机着陆后从开始滑行到停止,滑行的距离为( )
A.500米 B.600米 C.700米 D.800米
6.将函数y=3x2的图象先向右平移2个单位,再向上平移5个单位,所得图象的函数表达式是( )
A.y=3(x-2)2-5
B.y=3(x-2)2+5
C.y=3(x+2)2-5
D.y=3(x+2)2+5
7.已知二次函数y=2mx2+(4-m)x,它的图象可能是( )
8.已知抛物线y=ax2+bx+c(a,b,c为常数且a≠0)经过P1(1,y1),P2(2,y2),P3(3,y3),P4(4,y4)四点,若y3<y2<y1,则下列说法中一定正确的是( )
A.抛物线开口向下 B.对称轴为直线x=3
C.y1>y4 D.5a+b>0
9.如图,抛物线y=ax2+bx+c与x轴交于点A(-1,0),顶点坐标为(1,n),与y轴的交点在(0,3),(0,4)之间(包含端点),则下列结论:①abc>0;②2a+b=0;③-≤a≤-1;④a+b≥am2+bm(m为任意实数);⑤方程|ax2+bx+c|=n有四个不相等的实数根.其中正确的有( )
A.2个
B.3个
C.4个
D.5个
10.如图,在菱形ABCD中,AB=2 cm,∠D=60°,点P,Q同时从点A出发,点P以1 cm/s的速度沿A→C→D的方向运动,点Q以2 cm/s的速度沿A→B→C→D的方向运动,当其中一点到达点D时,两点停止运动.设运动时间为x(s),△APQ的面积为y(cm2),则下列图象中能大致反映y关于x的函数关系的是( )
二、填空题(每题4分,共24分)
11.已知函数y=x2+2x+1,当y=0时,x=________;当1
13.抛物线y=x2-3x+2与x轴的交点有________个.
14.如图,线段AB=8,点C是AB上一点,点D、E是线段AC的三等分点,分别以AD、DE、EC、CB为边作正方形,则AC=________时,四个正方形的面积之和最小.
15.对于二次函数y=x2-2mx-3,有下列说法:①它的图象与x轴有两个交点;②如果当x≤1时,y随x的增大而减小,则m=1;③若图象向左平移3个单位后过原点,则m=-1;④若当x=4时的函数值与当x=100时的函数值相等,则当x=104时的函数值为-3.其中正确说法的序号是________.
16.如图,抛物线y=x2+x-3与x轴交于A、B两点,与y轴交于点C,点D为抛物线上、第三象限内一动点,当∠ACD+2∠ABC=180°时,点D的坐标为________.
三、解答题(共66分)
17.(6分)在直角坐标系xOy中,二次函数y=x2+bx+c的图象过点A(1,0)和点B(0,-3).
(1)求此二次函数的表达式;
(2)设此二次函数图象的顶点为C,写出另一个过点C的二次函数的表达式.
18.(6分)已知二次函数y=-x2+2x+3.
(1)用描点法画出它的图象;
(2)该二次函数的顶点坐标是________,点P(2,3)________(填“在”或“不在”)该二次函数的图象上.
19.(6分)如图,抛物线y1=-2x2+2与直线y2=2x+2交于A,B两点.
(1)求A,B两点的坐标;
(2)若y1>y2,请直接写出x的取值范围.
20.(8分)在“乡村振兴”行动中,某村办企业以A,B两种农作物为原料,开发了一种有机产品.A原料的单价是B原料单价的1.5倍.若用900元收购A原料会比用900元收购B原料少100 kg,生产该产品每盒需要A原料2 kg和B原料
4 kg,每盒还需其他成本9元.经市场调查发现,该产品售价为每盒40元时,每天可卖出150盒.如果每盒的售价每涨1元(每盒售价不能高于45元),那么每天少卖10盒.设每盒涨价x元(x为非负整数),每天销售y盒.
(1)求该产品每盒的成本(成本=原料费+其他成本);
(2)求y关于x的函数表达式及自变量x的取值范围;
(3)销售价格定为每盒多少元时,才能使每天的利润最大且每天销量较大?每天的最大利润是多少元?
21.(8分)在平面直角坐标系xOy中,抛物线y=mx2-2mx-2m+1与x轴交于A,B两点.
(1)若AB=2,求m的值;
(2)过点P(0,2)作与x轴平行的直线,交抛物线于点M,N.当MN≥2时,求m的取值范围.
22.如图所示是隧道的截面,由抛物线和长方形构成,长方形的长是12 m,宽是
4 m.按照图中所示的直角坐标系,抛物线可以用y=-x2+bx+c表示,且抛物线上的点C到OB的水平距离为3 m,到地面OA的距离为 m.
(1)求抛物线的函数表达式,并计算出隧道顶点D到地面OA的距离;
(2)一辆货车载一长方体集装箱后高为6 m,宽为4 m,如果隧道内设双向车道,那么这辆货车能否安全通过?
(3)在隧道的抛物线形拱壁上需要安装两排灯,使它们离地面的高度相等,如果灯离地面的高度不超过8 m,那么两排灯的水平距离最小是多少米?
23.(10分)如图,在平面直角坐标系中,过原点的抛物线的顶点M的坐标为(-1,-1),点A的坐标为(1,1),以OA为边的菱形OABC的顶点C在x轴的正半轴上,把菱形OABC沿AB向上翻折得到菱形EABD.
(1)求抛物线对应的函数表达式;
(2)若把抛物线向右平移使抛物线经过点D,求平移的距离.
24.(12分)对于某一函数给出如下定义:如果存在实数p,当其自变量的值为p时,其函数值等于p,则称p为这个函数的不动值.在函数存在不动值时,该函数的最大不动值与最小不动值之差q称为这个函数的不动长度,特别地,当函数只有一个不动值时,其不动长度q为0.例如,下图中的函数有0和1两个不动值,其不动长度q为1.
(1)下列函数:①y=2x;②y=x2+1;③y=x2-2x.其中存在不动值的是________(填序号).
(2)函数y=3x2+bx,
①若其不动长度为0,则b的值为________.
②若-2≤b≤2,求其不动长度q的取值范围.
(3)记函数y=x2-4x(x≥m)的图象为G1,将G1沿x=m翻折后得到的函数图象记为G2,函数G的图象由G1和G2两部分组成,若其不动长度q满足0≤q≤5,则m的取值范围为________.
答案
一、1.B 2.D 3.C 4.D 5.B 6.B
7.B 8.C 9.B 10.A
二、11.-1;增大 12.x1=1,x2=3
13.2 14.6 15.①④ 16.
三、17.解:(1)把点A(1,0)的坐标和点B(0,-3)的坐标代入y=x2+bx+c,
得解得
∴此二次函数的表达式为y=x2+2x-3.
(2)y=x2+2x-3=(x+1)2-4,则此二次函数图象的顶点C的坐标为(-1,-4).
另一个过点C的二次函数的表达式为y=-(x+1)2-4(答案不唯一).
18.解:(1)列表:
x … -1 0 1 2 3 …
y … 0 3 4 3 0 …
描点,画图如下:
(2)(1,4);在
19.解:(1)由题可得
解得或
∴A,B两点的坐标分别是(-1,0),(0,2).
(2)由图可知,当y1>y2时,x的取值范围是-1<x<0.
20.解:(1)设B原料单价为每千克m元,则A原料单价为千克1.5m元,
根据题意,得-=100,
解得m=3.∴1.5m=1.5×3=4.5.
∴该产品每盒的成本为4.5×2+3×4+9=30(元).
答:该产品每盒的成本为30元.
(2)y关于x的函数表达式是y=150-10x(0≤x≤5,且x为整数).
(3)设每天的利润为w元,
则w=(40+x-30)(150-10x)
=-10x2+50x+1 500
=-102+(0≤x≤5,且x为整数),
∴当x=2或x=3时,w取得最大值,最大值为1 560.
又∵要求每天销量较大,∴x=2.
∴每盒定价为42元.
答:销售价格定为每盒42元时,才能使每天的利润最大且每天销量较大,每天的最大利润是1 560元.
21.解:(1)抛物线y=mx2-2mx-2m+1的对称轴为直线x=-=1.
∵点A,B关于直线x=1对称,AB=2,
∴抛物线与x轴交于点A(0,0),B(2,0).将A(0,0)的坐标代入y=mx2-2mx-2m+1中,得-2m+1=0,解得m=.
(2)∴抛物线y=mx2-2mx-2m+1与x轴有两个交点,
∴Δ>0,即(-2m)2-4m(-2m+1)>0,解得m>或m<0.
①若m>0,则抛物线开口向上.
当MN≥2时,有-2m+1≤2,
解得m≥-,∴m>;
②若m<0,则抛物线开口向下.
当MN≥2时,有-2m+1≥2,
解得m≤-,∴m≤-.
综上所述,m的取值范围为m>或m≤-.
22.解:(1)由题知点B(0,4),
C在抛物线上,
则有
解得
所以y=-x2+2x+4.
当x=-=6时,y=10.
即隧道顶点D到地面OA的距离为10 m.
(2)由题知货车最外侧与地面OA的交点为(2,0)或(10,0),
当x=2或x=10时,y=>6,
所以这辆货车能安全通过.
(3)令y=8,有-x2+2x+4=8,可得x2-12x+24=0,
解得x1=6+2 ,x2=6-2 ,
x1-x2=4 .
答:两排灯的水平距离最小是4 m.
23.解:(1)设抛物线对应的函数表达式为y=a(x+1)2-1,
把点O(0,0)的坐标代入,得a=1.
∴抛物线对应的函数表达式为y=(x+1)2-1.
(2)∵点A(1,1),∴OA=.
∵菱形EABD是由菱形OABC沿AB向上翻折得到,
∴OE=2,DE=OC=OA=.
∴点D的坐标为(,2).
设抛物线向右平移后得到的抛物线的函数表达式为y=(x+1-m)2-1.
由题意得(+1-m)2-1=2,
解得m1=+1+,m2=+1-.
∴平移的距离为+1+或+1-.
24.解:(1)①③
(2)① 1
②由题意得3x2+bx=x,解得x=0或x=.∴q=,
当-2≤b≤1时,q=,
此时0≤q≤1;
当1≤b≤2时,q=-,
此时0≤q≤.
综上,其不动长度q的取值范围为0≤q≤1.
(3)2≤m≤5或m<-.
PAGE
同课章节目录
