浙教A版九年级数学上册 第3章 圆的基本性质 达标检测卷(word版 含答案)
文档属性
| 名称 | 浙教A版九年级数学上册 第3章 圆的基本性质 达标检测卷(word版 含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 829.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-13 19:52:16 | ||
图片预览

文档简介
浙教A版九年级数学上册 第3章 达标检测卷
(限时: 120分钟 满分: 120分)
班级: 姓名: 得分:
一、单选题(每题3分,共30分)
1.已知⊙O的半径为5 cm,点A是线段OP的中点,当OP=8 cm时,点A与⊙O的位置关系是( )
A.点A在⊙O外 B.点A在⊙O上
C.点A在⊙O内 D.不能确定
2.圆内接正十边形的外角和为( )
A.180° B.360° C.720° D.1 440°
3.下列说法正确的是( )
A.等弧所对的圆心角相等
B.平分弦的直径垂直于这条弦
C.经过三点可以作一个圆
D.相等的圆心角所对的弧相等
4.如图,在4×4的正方形网格中,小正方形的边长为1,若将△ABC绕点A逆时针旋转得到△AB′C′,则的长为( )
A.π B. C.7π D.6π
5.如图,⊙O的半径为5,AB为弦,OC⊥AB,垂足为E,如果CE=2,那么AB的长是( )
A.4 B.6 C.8 D.10
6.如图,四边形ABDC是⊙O的内接四边形,∠BOC=110°,则∠BDC的度数是( )
A.110° B.70° C.55° D.125°
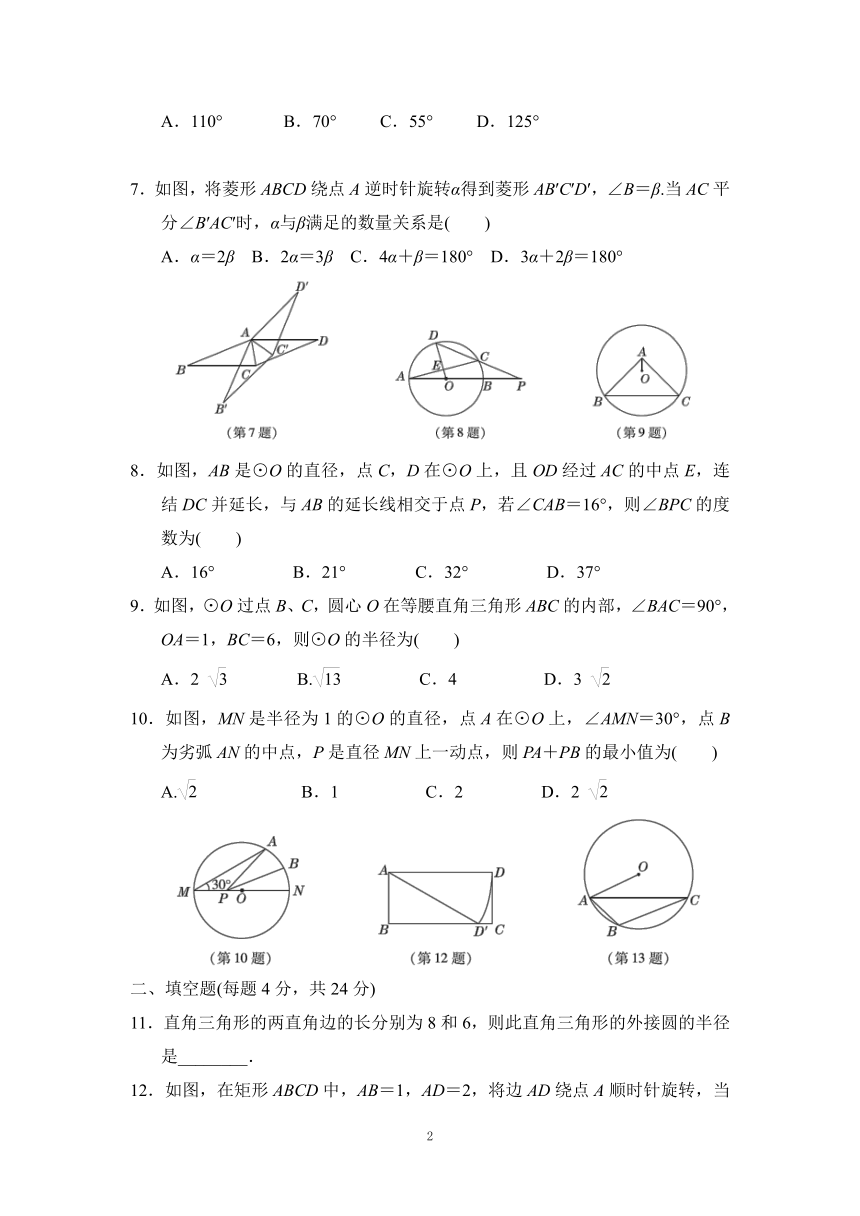
7.如图,将菱形ABCD绕点A逆时针旋转α得到菱形AB′C′D′,∠B=β.当AC平分∠B′AC′时,α与β满足的数量关系是( )
A.α=2β B.2α=3β C.4α+β=180° D.3α+2β=180°
8.如图,AB是⊙O的直径,点C,D在⊙O上,且OD经过AC的中点E,连结DC并延长,与AB的延长线相交于点P,若∠CAB=16°,则∠BPC的度数为( )
A.16° B.21° C.32° D.37°
9.如图,⊙O过点B、C,圆心O在等腰直角三角形ABC的内部,∠BAC=90°,OA=1,BC=6,则⊙O的半径为( )
A.2 B. C.4 D.3
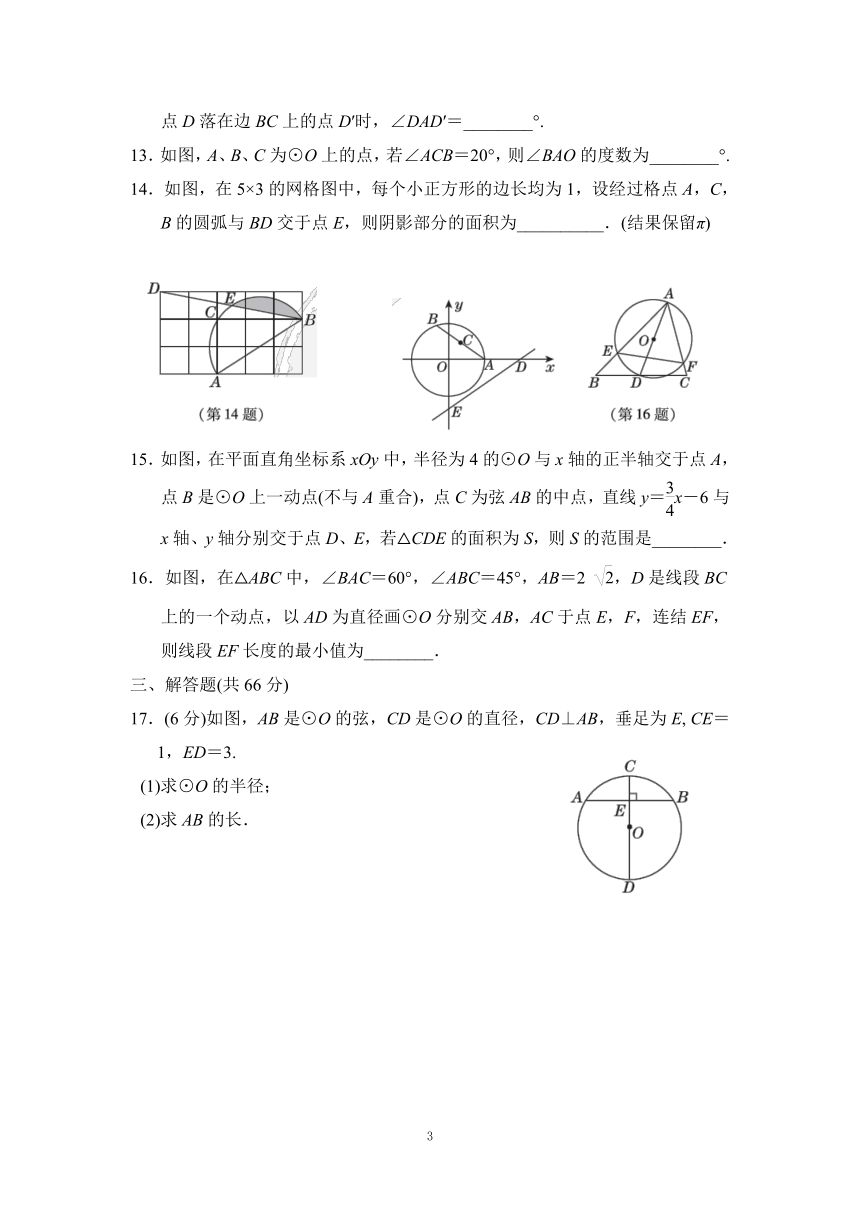
10.如图,MN是半径为1的⊙O的直径,点A在⊙O上,∠AMN=30°,点B为劣弧AN的中点,P是直径MN上一动点,则PA+PB的最小值为( )
A. B.1 C.2 D.2
二、填空题(每题4分,共24分)
11.直角三角形的两直角边的长分别为8和6,则此直角三角形的外接圆的半径是________.
12.如图,在矩形ABCD中,AB=1,AD=2,将边AD绕点A顺时针旋转,当点D落在边BC上的点D′时,∠DAD′=________°.
13.如图,A、B、C为⊙O上的点,若∠ACB=20°,则∠BAO的度数为________°.
14.如图,在5×3的网格图中,每个小正方形的边长均为1,设经过格点A,C,B的圆弧与BD交于点E,则阴影部分的面积为__________.(结果保留π)
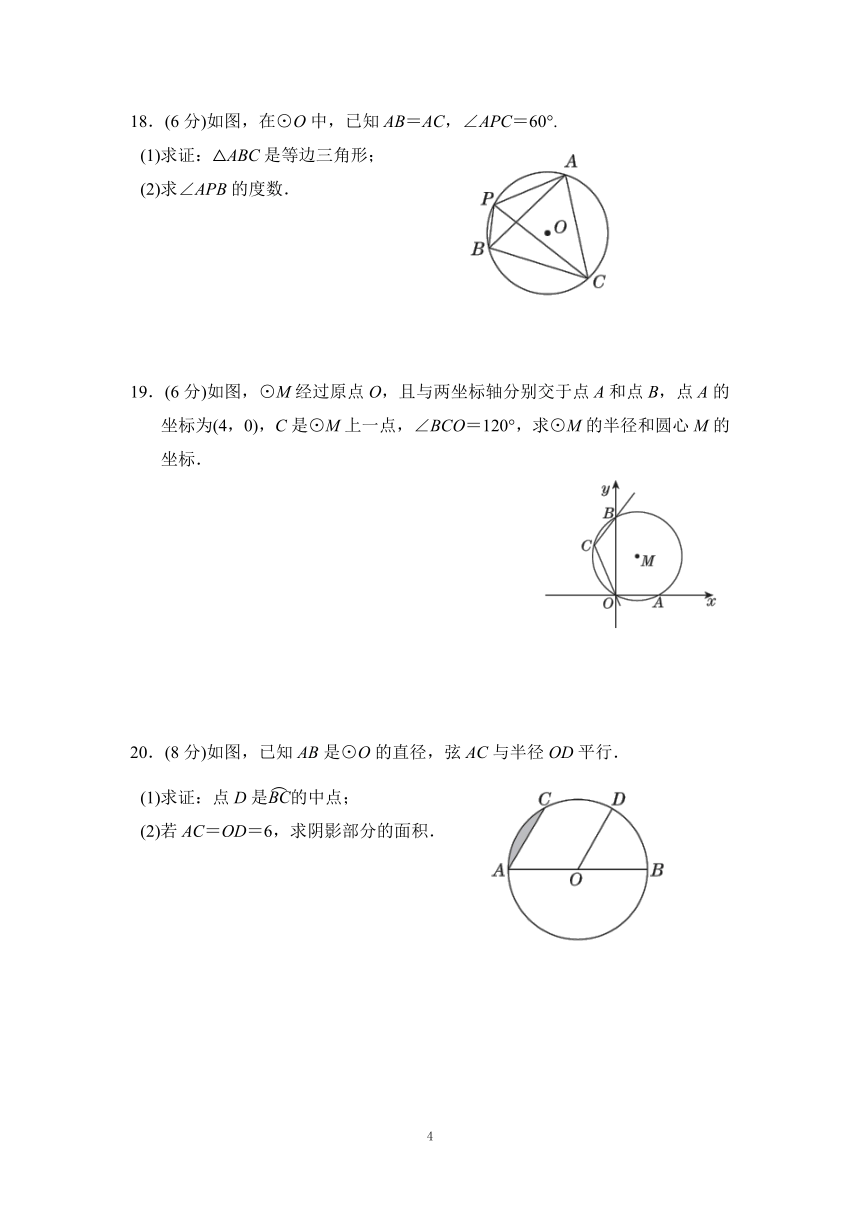
15.如图,在平面直角坐标系xOy中,半径为4的⊙O与x轴的正半轴交于点A,点B是⊙O上一动点(不与A重合),点C为弦AB的中点,直线y=x-6与x轴、y轴分别交于点D、E,若△CDE的面积为S,则S的范围是________.
16.如图,在△ABC中,∠BAC=60°,∠ABC=45°,AB=2 ,D是线段BC上的一个动点,以AD为直径画⊙O分别交AB,AC于点E,F,连结EF,则线段EF长度的最小值为________.
三、解答题(共66分)
17.(6分)如图,AB是⊙O的弦,CD是⊙O的直径,CD⊥AB,垂足为E, CE=1,ED=3.
(1)求⊙O的半径;
(2)求AB的长.
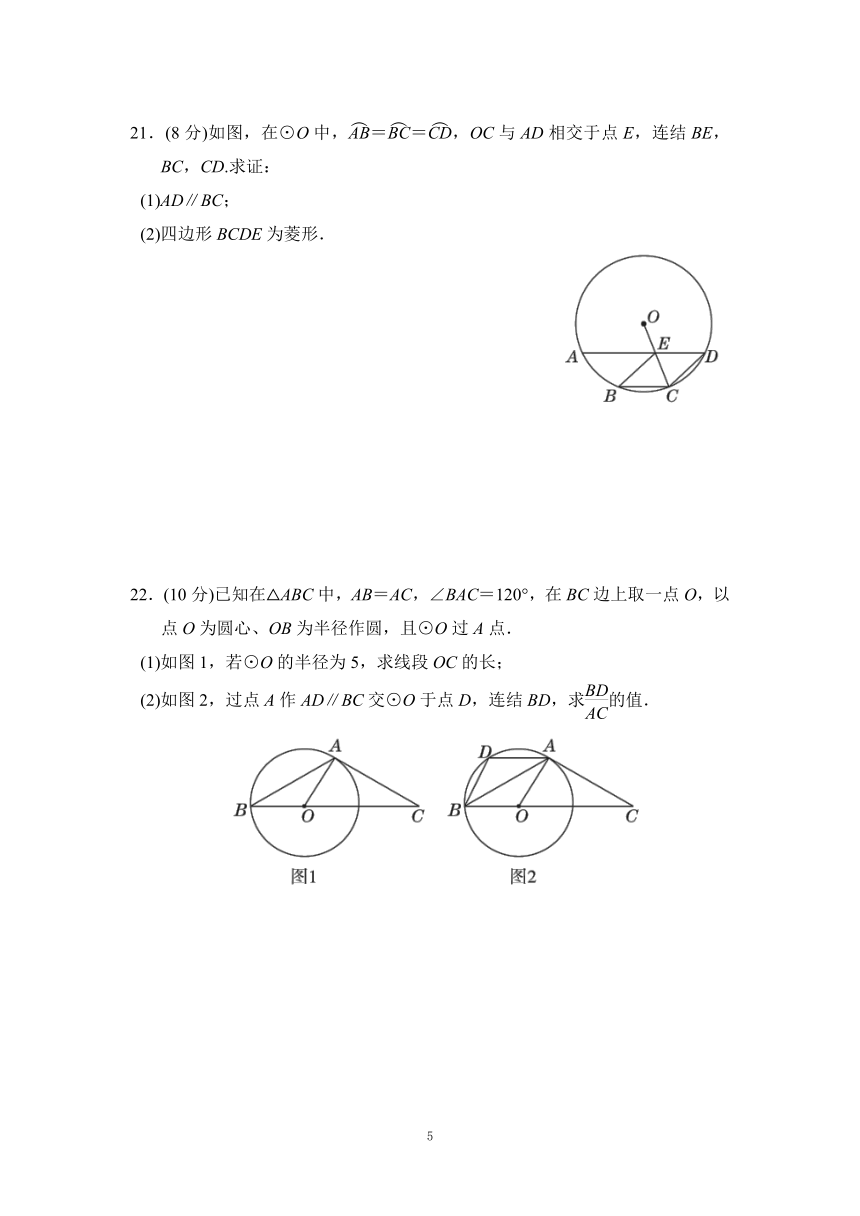
18.(6分)如图,在⊙O中,已知AB=AC,∠APC=60°.
(1)求证:△ABC是等边三角形;
(2)求∠APB的度数.
19.(6分)如图,⊙M经过原点O,且与两坐标轴分别交于点A和点B,点A的坐标为(4,0),C是⊙M上一点,∠BCO=120°,求⊙M的半径和圆心M的坐标.
20.(8分)如图,已知AB是⊙O的直径,弦AC与半径OD平行.
(1)求证:点D是的中点;
(2)若AC=OD=6,求阴影部分的面积.
21.(8分)如图,在⊙O中,==,OC与AD相交于点E,连结BE,BC,CD.求证:
(1)AD∥BC;
(2)四边形BCDE为菱形.
22.(10分)已知在△ABC中,AB=AC,∠BAC=120°,在BC边上取一点O,以点O为圆心、OB为半径作圆,且⊙O过A点.
(1)如图1,若⊙O的半径为5,求线段OC的长;
(2)如图2,过点A作AD∥BC交⊙O于点D,连结BD,求的值.
23.(10分)我们新定义一种三角形:两边的平方和等于第三边平方的两倍的三角形叫做奇异三角形.
(1)根据“奇异三角形”的定义,小华提出命题“等边三角形一定是奇异三角形”,这个命题是真命题还是假命题?
(2)在Rt△ABC中,∠C=90°,AB=c,AC=b,BC=a,且b>a,若Rt△ABC是奇异三角形,求a∶b∶c.
(3)如图,AB是⊙O的直径,C是⊙O上一点(不与点A、B重合),D是半圆的中点,C、D分别在直径AB的两侧,若在⊙O内存在点E,使AE=AD,CB=CE.
①求证:△ACE是奇异三角形;
②当△ACE是直角三角形时,求∠AOC的度数.
24.(12分)[问题提出]
如图1,AB,AC是⊙O的两条弦,AC>AB,M是的中点,MD⊥AC,垂足为D,求证:CD=BA+AD.
小敏在解答此题时,利用了“补短法”进行证明,她的方法如下:
证明:如图2,延长CA至E,使AE=AB,连结MA,MB,MC,ME,BC.
∵M是的中点,
∴=,∴∠MCB=∠MBC.(请你在下面的空白处完成小敏的证明过程)
[推广运用]
如图3,等边三角形ABC内接于⊙O,AB=1,D是上一点,∠ABD=45°,AE⊥BD,垂足为E,则△BDC的周长是________.
[拓展研究]
如图4,若将[问题提出]中的“M是的中点”改成“M是的中点”,其余条件不变,“CD=BA+AD”这一结论还成立吗?若成立,请说明理由;若不成立,写出CD,BA,AD三者之间的关系,并说明理由.
答案
一、1.C 2.B 3.A 4.A 5.C 6.D
7.C 8.B 9.B 10.A
二、11.5 12.30 13.70
14.- 15.8≤S≤2 16.
三、17.解:(1)∵CE=1,ED=3,
∴CD=CE+ED=4.
∴⊙O的半径为2.
(2)如图,连结OA,则OA=OC=2,
∴OE=OC-CE=2-1=1.
∵CD⊥AB,
∴AB=2AE,∠OEA=90°.
在Rt△OEA中,由勾股定理,得
AE===.
∴AB=2AE=2 .
18.(1)证明:∵∠APC=60°,
∴ ∠ABC=∠APC=60°.
∵AB=AC,
∴△ABC是等边三角形.
(2)解:由(1)知,∠ACB=∠ABC=60°.
∵四边形APBC是⊙O的内接四边形,∴∠APB+∠ACB=180°.
∴∠APB=180°-∠ACB=180°-60°=120°.
19.解:如图,连结AB.
∵BO⊥AO,
∴AB过圆心M,
即AB是⊙M的直径.
∵四边形ABCO是⊙O的内接四边形,且∠BCO=120°,
∴∠BAO=60°.
∴∠ABO=30°.
∴在Rt△ABO中,
AB=2OA=8.
∴⊙M的半径为4.
在Rt△ABO中,BO===4 .
如图,过点M作MN⊥AO,垂足为N.
∵M是AB的中点,且MN∥BO,
∴MN=BO=2 ,
ON=OA=2.
∴圆心M的坐标为(2, 2 ).
20.(1)证明:如图,连结CO,
∵AC∥OD,
∴∠A=∠DOB,∠ACO=∠DOC.
∵OA=OC,∴∠A=∠ACO,
∴∠DOB=∠DOC,∴=,
∴点D是的中点.
(2)解:如图,∵AC=OD=OC=OA=6,
∴△AOC是等边三角形,
∴∠AOC=60°,
∴S扇形AOC==6π.过点C作CE⊥AB于点E,则∠CEO=90°,∴∠OCE=30°,
∴OE=OC=×6=3,
∴CE==3 ,
∴S△AOC=OA·CE=×6×3 =9 ,
∴S阴影=S扇形AOC-S△AOC=6π-9 .
21.证明:(1)如图,连结BD,
∵==,
∴∠ADB=∠CBD,∴AD∥BC.
(2)如图,设OC与BD相交于点F.
∵=,∴BC=CD.
∴易得BF=DF.
又∵∠DFE=∠BFC,∠EDF=∠CBF,
∴△DEF≌△BCF.∴DE=BC.
∵AD∥BC,
∴四边形BCDE是平行四边形.
又∵BC=CD,
∴四边形BCDE是菱形.
22.解:(1)∵在△ABC中,AB=AC,∠BAC=120°,∴∠ABC=∠ACB=30°.
∵OA=OB,∴∠BAO=∠ABO=30°.
∴∠AOC=∠ABO+∠BAO=60°.
∴∠OAC=90°.
∵OA=5,∴OC=2OA=10.
(2)如图,连结OD.
∵∠AOC=60°,AD∥BC,
∴∠DAO=∠AOC=60°.
∵OD=OA,∴∠ADO=60°.
∴∠DOB=∠ADO=60°.
又∵OD=OB,
∴△DOB是等边三角形.
∴BD=OB=OA.
在Rt△OAC中,OC=2OA,
AC=OA,即AC=BD,∴=.
23.(1)解:这个命题是真命题.
(2)解:易知在Rt△ABC中,有a2+b2=c2.
∵c>b>a>0,
∴2c2>a2+b2,2a2∴若△ABC是奇异三角形,一定有2b2=a2+c2.
∴2b2=a2+(a2+b2).
∴b2=2a2,解得b=a.
∵c2=b2+a2=3a2,∴c=a.
∴a∶b∶c=1∶∶.
(3)①证明:∵AB是⊙O的直径,
∴∠ACB=∠ADB=90°.
在Rt△ACB中,AC2+BC2=AB2,
在Rt△ADB中,AD2+BD2=AB2.
∵D是半圆的中点,
∴=.∴AD=BD.
∴AB2=AD2+BD2=2AD2.
又∵CB=CE,AE=AD,
∴AC2+CE2=2AE2.
∴△ACE是奇异三角形.
②解:由①可得△ACE是奇异三角形,且AC2+CE2=2AE2.
当△ACE是直角三角形时,
由(2)可得AC∶AE∶CE=1∶∶或AC∶AE∶CE=∶∶ 1.
(Ⅰ)当AC∶AE∶CE=1∶∶时,
AC∶CE=1∶,即AC∶CB=1∶.
∵∠ACB=90°,∴∠ABC=30°.
∴∠AOC=2∠ABC=60°.
(Ⅱ)当AC∶AE∶CE=∶∶1时,
AC∶CE=∶1,即AC∶CB=∶1.∵∠ACB=90°,∴∠ABC=60°.
∴∠AOC=2∠ABC=120°.
∴∠AOC的度数为60°或120°.
24.解:【问题提出】证明:如图2,延长CA至E,使AE=AB,连结MA,MB,MC,ME,BC,
∵M是的中点,
∴=,∴∠MCB=∠MBC.
∴MB=MC.
∵∠BAM=180°-∠MCB,∠EAM=180°-∠MAC=180°-∠MBC,
∴∠EAM=∠BAM.
在△EAM和△BAM中,
∴△EAM≌△BAM,
∴ME=MB=MC.
又∵MD⊥AC,∴ED=CD,
∴CD=AD+AE=BA+AD.
【推广运用】1+
【拓展研究】不成立,CD,BA,AD三者之间的关系:AD=BA+CD,
理由:如图4,延长MD交⊙O于点E,连结EA,EC,连结EB交AC于点N.
∵M是的中点,∴=.
∴∠BEM=∠CEM.
在△EDN和△EDC中,
∴△EDN≌△EDC,
∴ND=CD,∠END=∠ECD.
∵∠ECD=∠ABE,∠ENC=∠ANB,
∴∠ANB=∠ABE,∴AN=AB,
∴AD=AN+ND=BA+CD.
PAGE
(限时: 120分钟 满分: 120分)
班级: 姓名: 得分:
一、单选题(每题3分,共30分)
1.已知⊙O的半径为5 cm,点A是线段OP的中点,当OP=8 cm时,点A与⊙O的位置关系是( )
A.点A在⊙O外 B.点A在⊙O上
C.点A在⊙O内 D.不能确定
2.圆内接正十边形的外角和为( )
A.180° B.360° C.720° D.1 440°
3.下列说法正确的是( )
A.等弧所对的圆心角相等
B.平分弦的直径垂直于这条弦
C.经过三点可以作一个圆
D.相等的圆心角所对的弧相等
4.如图,在4×4的正方形网格中,小正方形的边长为1,若将△ABC绕点A逆时针旋转得到△AB′C′,则的长为( )
A.π B. C.7π D.6π
5.如图,⊙O的半径为5,AB为弦,OC⊥AB,垂足为E,如果CE=2,那么AB的长是( )
A.4 B.6 C.8 D.10
6.如图,四边形ABDC是⊙O的内接四边形,∠BOC=110°,则∠BDC的度数是( )
A.110° B.70° C.55° D.125°
7.如图,将菱形ABCD绕点A逆时针旋转α得到菱形AB′C′D′,∠B=β.当AC平分∠B′AC′时,α与β满足的数量关系是( )
A.α=2β B.2α=3β C.4α+β=180° D.3α+2β=180°
8.如图,AB是⊙O的直径,点C,D在⊙O上,且OD经过AC的中点E,连结DC并延长,与AB的延长线相交于点P,若∠CAB=16°,则∠BPC的度数为( )
A.16° B.21° C.32° D.37°
9.如图,⊙O过点B、C,圆心O在等腰直角三角形ABC的内部,∠BAC=90°,OA=1,BC=6,则⊙O的半径为( )
A.2 B. C.4 D.3
10.如图,MN是半径为1的⊙O的直径,点A在⊙O上,∠AMN=30°,点B为劣弧AN的中点,P是直径MN上一动点,则PA+PB的最小值为( )
A. B.1 C.2 D.2
二、填空题(每题4分,共24分)
11.直角三角形的两直角边的长分别为8和6,则此直角三角形的外接圆的半径是________.
12.如图,在矩形ABCD中,AB=1,AD=2,将边AD绕点A顺时针旋转,当点D落在边BC上的点D′时,∠DAD′=________°.
13.如图,A、B、C为⊙O上的点,若∠ACB=20°,则∠BAO的度数为________°.
14.如图,在5×3的网格图中,每个小正方形的边长均为1,设经过格点A,C,B的圆弧与BD交于点E,则阴影部分的面积为__________.(结果保留π)
15.如图,在平面直角坐标系xOy中,半径为4的⊙O与x轴的正半轴交于点A,点B是⊙O上一动点(不与A重合),点C为弦AB的中点,直线y=x-6与x轴、y轴分别交于点D、E,若△CDE的面积为S,则S的范围是________.
16.如图,在△ABC中,∠BAC=60°,∠ABC=45°,AB=2 ,D是线段BC上的一个动点,以AD为直径画⊙O分别交AB,AC于点E,F,连结EF,则线段EF长度的最小值为________.
三、解答题(共66分)
17.(6分)如图,AB是⊙O的弦,CD是⊙O的直径,CD⊥AB,垂足为E, CE=1,ED=3.
(1)求⊙O的半径;
(2)求AB的长.
18.(6分)如图,在⊙O中,已知AB=AC,∠APC=60°.
(1)求证:△ABC是等边三角形;
(2)求∠APB的度数.
19.(6分)如图,⊙M经过原点O,且与两坐标轴分别交于点A和点B,点A的坐标为(4,0),C是⊙M上一点,∠BCO=120°,求⊙M的半径和圆心M的坐标.
20.(8分)如图,已知AB是⊙O的直径,弦AC与半径OD平行.
(1)求证:点D是的中点;
(2)若AC=OD=6,求阴影部分的面积.
21.(8分)如图,在⊙O中,==,OC与AD相交于点E,连结BE,BC,CD.求证:
(1)AD∥BC;
(2)四边形BCDE为菱形.
22.(10分)已知在△ABC中,AB=AC,∠BAC=120°,在BC边上取一点O,以点O为圆心、OB为半径作圆,且⊙O过A点.
(1)如图1,若⊙O的半径为5,求线段OC的长;
(2)如图2,过点A作AD∥BC交⊙O于点D,连结BD,求的值.
23.(10分)我们新定义一种三角形:两边的平方和等于第三边平方的两倍的三角形叫做奇异三角形.
(1)根据“奇异三角形”的定义,小华提出命题“等边三角形一定是奇异三角形”,这个命题是真命题还是假命题?
(2)在Rt△ABC中,∠C=90°,AB=c,AC=b,BC=a,且b>a,若Rt△ABC是奇异三角形,求a∶b∶c.
(3)如图,AB是⊙O的直径,C是⊙O上一点(不与点A、B重合),D是半圆的中点,C、D分别在直径AB的两侧,若在⊙O内存在点E,使AE=AD,CB=CE.
①求证:△ACE是奇异三角形;
②当△ACE是直角三角形时,求∠AOC的度数.
24.(12分)[问题提出]
如图1,AB,AC是⊙O的两条弦,AC>AB,M是的中点,MD⊥AC,垂足为D,求证:CD=BA+AD.
小敏在解答此题时,利用了“补短法”进行证明,她的方法如下:
证明:如图2,延长CA至E,使AE=AB,连结MA,MB,MC,ME,BC.
∵M是的中点,
∴=,∴∠MCB=∠MBC.(请你在下面的空白处完成小敏的证明过程)
[推广运用]
如图3,等边三角形ABC内接于⊙O,AB=1,D是上一点,∠ABD=45°,AE⊥BD,垂足为E,则△BDC的周长是________.
[拓展研究]
如图4,若将[问题提出]中的“M是的中点”改成“M是的中点”,其余条件不变,“CD=BA+AD”这一结论还成立吗?若成立,请说明理由;若不成立,写出CD,BA,AD三者之间的关系,并说明理由.
答案
一、1.C 2.B 3.A 4.A 5.C 6.D
7.C 8.B 9.B 10.A
二、11.5 12.30 13.70
14.- 15.8≤S≤2 16.
三、17.解:(1)∵CE=1,ED=3,
∴CD=CE+ED=4.
∴⊙O的半径为2.
(2)如图,连结OA,则OA=OC=2,
∴OE=OC-CE=2-1=1.
∵CD⊥AB,
∴AB=2AE,∠OEA=90°.
在Rt△OEA中,由勾股定理,得
AE===.
∴AB=2AE=2 .
18.(1)证明:∵∠APC=60°,
∴ ∠ABC=∠APC=60°.
∵AB=AC,
∴△ABC是等边三角形.
(2)解:由(1)知,∠ACB=∠ABC=60°.
∵四边形APBC是⊙O的内接四边形,∴∠APB+∠ACB=180°.
∴∠APB=180°-∠ACB=180°-60°=120°.
19.解:如图,连结AB.
∵BO⊥AO,
∴AB过圆心M,
即AB是⊙M的直径.
∵四边形ABCO是⊙O的内接四边形,且∠BCO=120°,
∴∠BAO=60°.
∴∠ABO=30°.
∴在Rt△ABO中,
AB=2OA=8.
∴⊙M的半径为4.
在Rt△ABO中,BO===4 .
如图,过点M作MN⊥AO,垂足为N.
∵M是AB的中点,且MN∥BO,
∴MN=BO=2 ,
ON=OA=2.
∴圆心M的坐标为(2, 2 ).
20.(1)证明:如图,连结CO,
∵AC∥OD,
∴∠A=∠DOB,∠ACO=∠DOC.
∵OA=OC,∴∠A=∠ACO,
∴∠DOB=∠DOC,∴=,
∴点D是的中点.
(2)解:如图,∵AC=OD=OC=OA=6,
∴△AOC是等边三角形,
∴∠AOC=60°,
∴S扇形AOC==6π.过点C作CE⊥AB于点E,则∠CEO=90°,∴∠OCE=30°,
∴OE=OC=×6=3,
∴CE==3 ,
∴S△AOC=OA·CE=×6×3 =9 ,
∴S阴影=S扇形AOC-S△AOC=6π-9 .
21.证明:(1)如图,连结BD,
∵==,
∴∠ADB=∠CBD,∴AD∥BC.
(2)如图,设OC与BD相交于点F.
∵=,∴BC=CD.
∴易得BF=DF.
又∵∠DFE=∠BFC,∠EDF=∠CBF,
∴△DEF≌△BCF.∴DE=BC.
∵AD∥BC,
∴四边形BCDE是平行四边形.
又∵BC=CD,
∴四边形BCDE是菱形.
22.解:(1)∵在△ABC中,AB=AC,∠BAC=120°,∴∠ABC=∠ACB=30°.
∵OA=OB,∴∠BAO=∠ABO=30°.
∴∠AOC=∠ABO+∠BAO=60°.
∴∠OAC=90°.
∵OA=5,∴OC=2OA=10.
(2)如图,连结OD.
∵∠AOC=60°,AD∥BC,
∴∠DAO=∠AOC=60°.
∵OD=OA,∴∠ADO=60°.
∴∠DOB=∠ADO=60°.
又∵OD=OB,
∴△DOB是等边三角形.
∴BD=OB=OA.
在Rt△OAC中,OC=2OA,
AC=OA,即AC=BD,∴=.
23.(1)解:这个命题是真命题.
(2)解:易知在Rt△ABC中,有a2+b2=c2.
∵c>b>a>0,
∴2c2>a2+b2,2a2
∴2b2=a2+(a2+b2).
∴b2=2a2,解得b=a.
∵c2=b2+a2=3a2,∴c=a.
∴a∶b∶c=1∶∶.
(3)①证明:∵AB是⊙O的直径,
∴∠ACB=∠ADB=90°.
在Rt△ACB中,AC2+BC2=AB2,
在Rt△ADB中,AD2+BD2=AB2.
∵D是半圆的中点,
∴=.∴AD=BD.
∴AB2=AD2+BD2=2AD2.
又∵CB=CE,AE=AD,
∴AC2+CE2=2AE2.
∴△ACE是奇异三角形.
②解:由①可得△ACE是奇异三角形,且AC2+CE2=2AE2.
当△ACE是直角三角形时,
由(2)可得AC∶AE∶CE=1∶∶或AC∶AE∶CE=∶∶ 1.
(Ⅰ)当AC∶AE∶CE=1∶∶时,
AC∶CE=1∶,即AC∶CB=1∶.
∵∠ACB=90°,∴∠ABC=30°.
∴∠AOC=2∠ABC=60°.
(Ⅱ)当AC∶AE∶CE=∶∶1时,
AC∶CE=∶1,即AC∶CB=∶1.∵∠ACB=90°,∴∠ABC=60°.
∴∠AOC=2∠ABC=120°.
∴∠AOC的度数为60°或120°.
24.解:【问题提出】证明:如图2,延长CA至E,使AE=AB,连结MA,MB,MC,ME,BC,
∵M是的中点,
∴=,∴∠MCB=∠MBC.
∴MB=MC.
∵∠BAM=180°-∠MCB,∠EAM=180°-∠MAC=180°-∠MBC,
∴∠EAM=∠BAM.
在△EAM和△BAM中,
∴△EAM≌△BAM,
∴ME=MB=MC.
又∵MD⊥AC,∴ED=CD,
∴CD=AD+AE=BA+AD.
【推广运用】1+
【拓展研究】不成立,CD,BA,AD三者之间的关系:AD=BA+CD,
理由:如图4,延长MD交⊙O于点E,连结EA,EC,连结EB交AC于点N.
∵M是的中点,∴=.
∴∠BEM=∠CEM.
在△EDN和△EDC中,
∴△EDN≌△EDC,
∴ND=CD,∠END=∠ECD.
∵∠ECD=∠ABE,∠ENC=∠ANB,
∴∠ANB=∠ABE,∴AN=AB,
∴AD=AN+ND=BA+CD.
PAGE
同课章节目录
