浙教版数学八年级下册 3.2中位数和众数 课件(共18张PPT)
文档属性
| 名称 | 浙教版数学八年级下册 3.2中位数和众数 课件(共18张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 237.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-15 16:57:44 | ||
图片预览




文档简介
(共18张PPT)
3.2中位数和众数
平均数
“权”越大,对平均数的影响就越大
( 表示权)
加权平均数
老师带着一群幼儿园小朋友在公园里玩游戏,他们的年龄分别是(岁):39,5,6,6,5,6,5,6,6,6.
能用平均数表示这一群体的年龄特征吗
=9岁
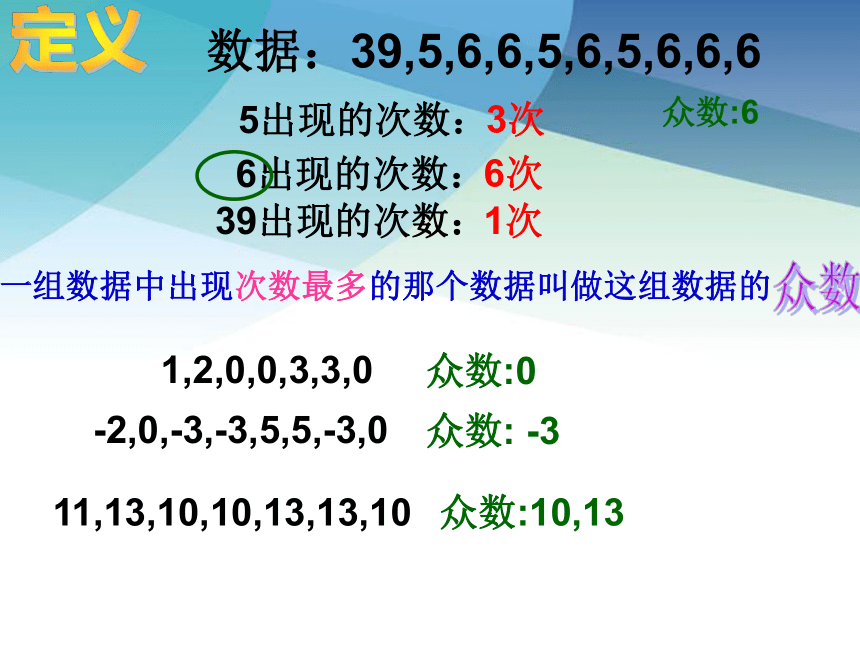
定义
一组数据中出现次数最多的那个数据叫做这组数据的
数据:39,5,6,6,5,6,5,6,6,6
5出现的次数:
3次
6出现的次数:
6次
39出现的次数:
1次
众数
众数:6
1,2,0,0,3,3,0
众数:0
-2,0,-3,-3,5,5,-3,0
众数: -3
11,13,10,10,13,13,10
众数:10,13
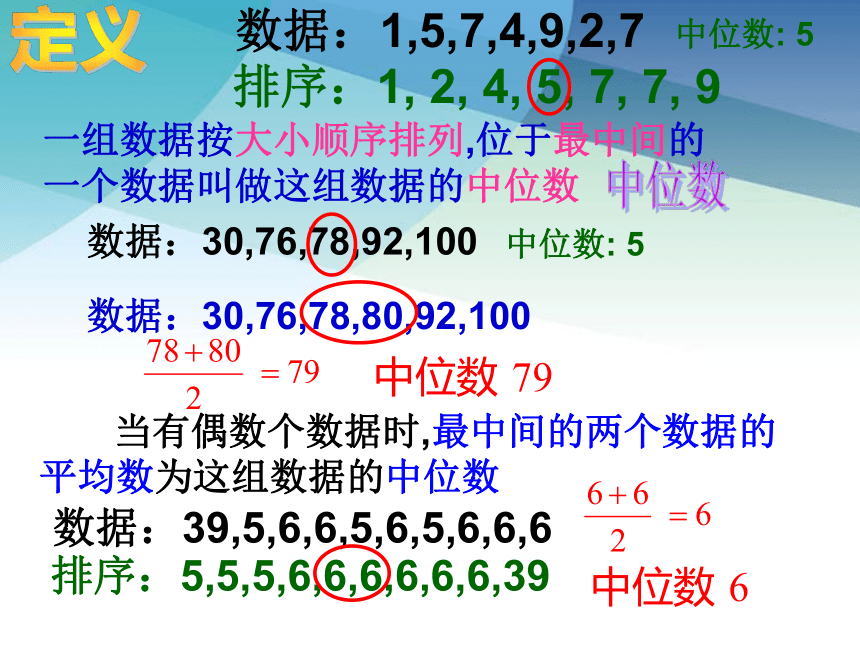
一组数据按大小顺序排列,位于最中间的
一个数据叫做这组数据的中位数
当有偶数个数据时,最中间的两个数据的
平均数为这组数据的中位数
数据:30,76,78,92,100
数据:30,76,78,80,92,100
定义
数据:39,5,6,6,5,6,5,6,6,6
排序:5,5,5,6,6,6,6,6,6,39
数据:1,5,7,4,9,2,7
排序:1, 2, 4, 5, 7, 7, 9
中位数
中位数: 5
中位数: 5
数 据
众数
中位数
15,20,22,20,35
20,15,20,35,22,38
15,20,20,22,35,35
20
21
21
【跟踪练习】
20
20
20和35
众数是否唯一?
p58做一做
p59例
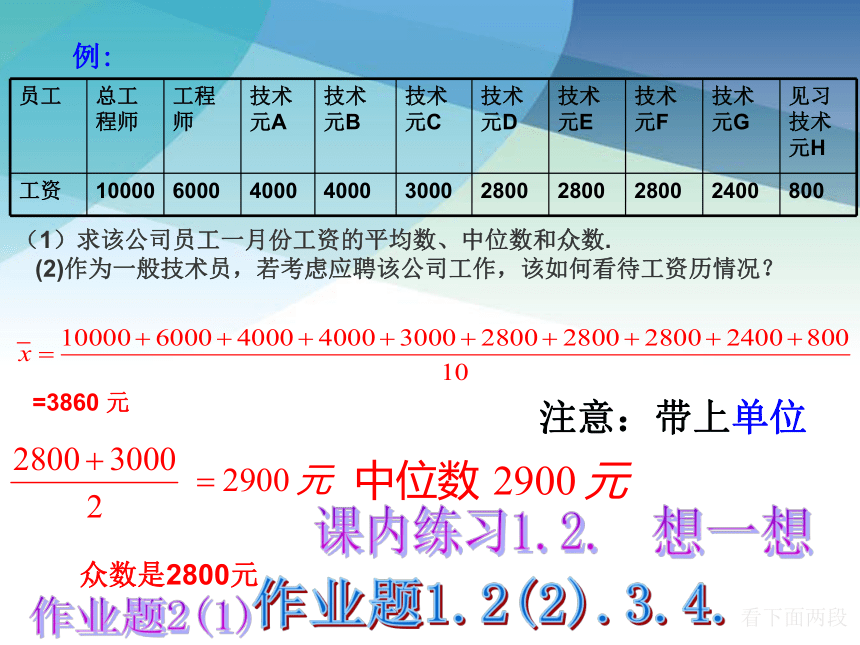
例:
=3860 元
众数是2800元
(1)求该公司员工一月份工资的平均数、中位数和众数.
(2)作为一般技术员,若考虑应聘该公司工作,该如何看待工资历情况?
员工 总工程师 工程师 技术元A 技术元B 技术元C 技术元D 技术元E 技术元F 技术元G 见习技术元H
工资 10000 6000 4000 4000 3000 2800 2800 2800 2400 800
注意:带上单位
看下面两段
想一想
课内练习1.2.
作业题2(1)
作业题1.2(2).3.4.
(1)一组数据的中位数只有一个。
(2)一组数据的中位数一定是这组数
据中的某个数据。
(3)一组数据的众数只有一个。
(4)一组数据的众数一定是这组数据
中的某个数 。
(5)一组数据的中位数、众数可以是同
一个数据。
(6)中位数和众数没有单位。
√
×
√
√
×
1,判断正误,并说明理由。
×
小结
平均数——
中位数——
众数——
对这组数据所包含的信息的反映最为充分,因而其应用最为广泛,但计算比较烦琐,并且容易受到极端数据的影响。
可靠性比较差,但众数不受极端数据的影响,并且求法简便。
仅与数据的排列位置有关,某些数据
的变动对它中位数没有影响。
集中趋势 相同点 求法 个数 优点 缺点 弥补的方法
平均数
中位数
众数
平均数、众数、中位数比较
是数据
的代表,
从不同
的侧面
反映了
数据的
集中程
度
当有多个众数没有多大意义
公式
先排序,找中间
个数最多的
1个
1个
0,1个及多个
能反映总体的水平的高低
能反映一个数据在这组数的位置
能反映相同数据的集中情况
容易受极端数据的影响
不能全面反映数据
去掉极端数据再算
与众数平均数联系着看
与中位数、平均数联系着看
测一测
1、简答题,请说明理由:(1) 河水的平均深度为2.5米,一个身高1.5米但不会游泳的人下水后肯定会淹死吗?
(2) 某校录取新生的平均成绩是535分,如果某人的考分是531分,他肯定没有被这个学校录取吗?
(3) 5位学生在一次考试中的得分分别是: 18,73,78,90,100,考分为73的同学是在平均分之上还是之下?你认为他在5人中考分属“中上”水平吗?
(4)9位学生的鞋号由小到大是:20,21,21,22,22,22,22,23,23,这组数据的平均数、中位数和众数中哪个指标是鞋厂最不感兴趣的?哪个指标是鞋厂最感兴趣的?
某车间为了改变管理松散的状况,准备采取每天任务定额,超产有奖的措施,提高工作率,下面是该车间15名工人过去一天中各自装配机器的数量(单位:台)
6、7、7、8、8、8、8、9、10、10、13、14、16、16、17
管理者应确定每个人标准日产量为多少台最好?
思考
平均数:
众数:
中位数
10. 5
8
9
测一测
(1) 为筹备班级里的新年晚会,班长对全班同学爱吃哪几种水果作了民意调查,最终买什么水果,该由调查数据的平均数,中位数还是众数决定呢?
(2)那边草地上有六个人正在玩游戏,他们的年龄的平均数是15岁,请想像一下是怎样的年龄的六个人在玩游戏,
(3)八年级有四个班级,如果已知一次测验中这四个班级每班的平均分,也知道各班级的学生人数,我们能否计算整个年级的平均分,
是不是六个十五岁的孩子?
也可以是一个65岁的大娘领着五个5岁的孩子在玩游戏。
如果已知的是每个班级
的中位数或者众数呢,能否知道整个年级中位数或者
众数呢。
某大商场策划了一次“还利给顾客”活动,凡一次购物100元以上(含100元)均可当场抽奖。奖金分配见下表:
奖金
等级
一等奖
二等奖
三等奖
四等奖
幸运奖
奖金数额/元
15000
8000
1000
80
20
中奖
人次
4
10
70
360
560
商场欺骗顾客了吗?
商场提醒:平均每份奖金249元!
应用
你认为商场的说法能够很好的代表中奖的一般金额吗?商场欺骗顾客了吗?说说你的看法,以后我们在遇到开奖问题应该关心什么?
中奖
顾客
商场在欺骗我们顾客,我们中只有两人获得80元,其他人都是20元,可气!
商场没有欺骗顾客,因为奖金的平均数确实是249元,但是奖金的平均数不能很好地代表中奖的一般金额,91.6%的奖卷的奖金不超过80元。如果遇到开奖问题应该关心中奖金额的众数等数据信息。
奖金
等级
一等奖
二等奖
三等奖
四等奖
幸运奖
奖金数额/元
15000
8000
1000
80
20
中奖
人次
4
10
70
360
560
平均数、中位数和众数的异同点:
(1)平均数、众数和中位数都是描述一组数据集中趋势的量;
(2)平均数、众数和中位数都有单位;
(3)平均数反映一组数据的平均水平,与这组数据中的每个数都有关系,所以应用最广,但它受极端值的影响较大;
(4)中位数只要很少计算,不受极端值影响;
(5)众数往往是我们最为关心的数据,它与各组数据出现的频数有关,不受极端值的影响.
谢谢!
3.2中位数和众数
平均数
“权”越大,对平均数的影响就越大
( 表示权)
加权平均数
老师带着一群幼儿园小朋友在公园里玩游戏,他们的年龄分别是(岁):39,5,6,6,5,6,5,6,6,6.
能用平均数表示这一群体的年龄特征吗
=9岁
定义
一组数据中出现次数最多的那个数据叫做这组数据的
数据:39,5,6,6,5,6,5,6,6,6
5出现的次数:
3次
6出现的次数:
6次
39出现的次数:
1次
众数
众数:6
1,2,0,0,3,3,0
众数:0
-2,0,-3,-3,5,5,-3,0
众数: -3
11,13,10,10,13,13,10
众数:10,13
一组数据按大小顺序排列,位于最中间的
一个数据叫做这组数据的中位数
当有偶数个数据时,最中间的两个数据的
平均数为这组数据的中位数
数据:30,76,78,92,100
数据:30,76,78,80,92,100
定义
数据:39,5,6,6,5,6,5,6,6,6
排序:5,5,5,6,6,6,6,6,6,39
数据:1,5,7,4,9,2,7
排序:1, 2, 4, 5, 7, 7, 9
中位数
中位数: 5
中位数: 5
数 据
众数
中位数
15,20,22,20,35
20,15,20,35,22,38
15,20,20,22,35,35
20
21
21
【跟踪练习】
20
20
20和35
众数是否唯一?
p58做一做
p59例
例:
=3860 元
众数是2800元
(1)求该公司员工一月份工资的平均数、中位数和众数.
(2)作为一般技术员,若考虑应聘该公司工作,该如何看待工资历情况?
员工 总工程师 工程师 技术元A 技术元B 技术元C 技术元D 技术元E 技术元F 技术元G 见习技术元H
工资 10000 6000 4000 4000 3000 2800 2800 2800 2400 800
注意:带上单位
看下面两段
想一想
课内练习1.2.
作业题2(1)
作业题1.2(2).3.4.
(1)一组数据的中位数只有一个。
(2)一组数据的中位数一定是这组数
据中的某个数据。
(3)一组数据的众数只有一个。
(4)一组数据的众数一定是这组数据
中的某个数 。
(5)一组数据的中位数、众数可以是同
一个数据。
(6)中位数和众数没有单位。
√
×
√
√
×
1,判断正误,并说明理由。
×
小结
平均数——
中位数——
众数——
对这组数据所包含的信息的反映最为充分,因而其应用最为广泛,但计算比较烦琐,并且容易受到极端数据的影响。
可靠性比较差,但众数不受极端数据的影响,并且求法简便。
仅与数据的排列位置有关,某些数据
的变动对它中位数没有影响。
集中趋势 相同点 求法 个数 优点 缺点 弥补的方法
平均数
中位数
众数
平均数、众数、中位数比较
是数据
的代表,
从不同
的侧面
反映了
数据的
集中程
度
当有多个众数没有多大意义
公式
先排序,找中间
个数最多的
1个
1个
0,1个及多个
能反映总体的水平的高低
能反映一个数据在这组数的位置
能反映相同数据的集中情况
容易受极端数据的影响
不能全面反映数据
去掉极端数据再算
与众数平均数联系着看
与中位数、平均数联系着看
测一测
1、简答题,请说明理由:(1) 河水的平均深度为2.5米,一个身高1.5米但不会游泳的人下水后肯定会淹死吗?
(2) 某校录取新生的平均成绩是535分,如果某人的考分是531分,他肯定没有被这个学校录取吗?
(3) 5位学生在一次考试中的得分分别是: 18,73,78,90,100,考分为73的同学是在平均分之上还是之下?你认为他在5人中考分属“中上”水平吗?
(4)9位学生的鞋号由小到大是:20,21,21,22,22,22,22,23,23,这组数据的平均数、中位数和众数中哪个指标是鞋厂最不感兴趣的?哪个指标是鞋厂最感兴趣的?
某车间为了改变管理松散的状况,准备采取每天任务定额,超产有奖的措施,提高工作率,下面是该车间15名工人过去一天中各自装配机器的数量(单位:台)
6、7、7、8、8、8、8、9、10、10、13、14、16、16、17
管理者应确定每个人标准日产量为多少台最好?
思考
平均数:
众数:
中位数
10. 5
8
9
测一测
(1) 为筹备班级里的新年晚会,班长对全班同学爱吃哪几种水果作了民意调查,最终买什么水果,该由调查数据的平均数,中位数还是众数决定呢?
(2)那边草地上有六个人正在玩游戏,他们的年龄的平均数是15岁,请想像一下是怎样的年龄的六个人在玩游戏,
(3)八年级有四个班级,如果已知一次测验中这四个班级每班的平均分,也知道各班级的学生人数,我们能否计算整个年级的平均分,
是不是六个十五岁的孩子?
也可以是一个65岁的大娘领着五个5岁的孩子在玩游戏。
如果已知的是每个班级
的中位数或者众数呢,能否知道整个年级中位数或者
众数呢。
某大商场策划了一次“还利给顾客”活动,凡一次购物100元以上(含100元)均可当场抽奖。奖金分配见下表:
奖金
等级
一等奖
二等奖
三等奖
四等奖
幸运奖
奖金数额/元
15000
8000
1000
80
20
中奖
人次
4
10
70
360
560
商场欺骗顾客了吗?
商场提醒:平均每份奖金249元!
应用
你认为商场的说法能够很好的代表中奖的一般金额吗?商场欺骗顾客了吗?说说你的看法,以后我们在遇到开奖问题应该关心什么?
中奖
顾客
商场在欺骗我们顾客,我们中只有两人获得80元,其他人都是20元,可气!
商场没有欺骗顾客,因为奖金的平均数确实是249元,但是奖金的平均数不能很好地代表中奖的一般金额,91.6%的奖卷的奖金不超过80元。如果遇到开奖问题应该关心中奖金额的众数等数据信息。
奖金
等级
一等奖
二等奖
三等奖
四等奖
幸运奖
奖金数额/元
15000
8000
1000
80
20
中奖
人次
4
10
70
360
560
平均数、中位数和众数的异同点:
(1)平均数、众数和中位数都是描述一组数据集中趋势的量;
(2)平均数、众数和中位数都有单位;
(3)平均数反映一组数据的平均水平,与这组数据中的每个数都有关系,所以应用最广,但它受极端值的影响较大;
(4)中位数只要很少计算,不受极端值影响;
(5)众数往往是我们最为关心的数据,它与各组数据出现的频数有关,不受极端值的影响.
谢谢!
同课章节目录
- 第一章 二次根式
- 1.1 二次根式
- 1.2 二次根式的性质
- 1.3 二次根式的运算
- 第二章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程的应用
- 2.4 一元二次方程根与系数的关系(选学)
- 第三章 数据分析初步
- 3.1 平均数
- 3.2 中位数和众数
- 3.3 方差和标准差
- 第四章 平行四边形
- 4.1 多边形
- 4.2 平行四边形
- 4.3 中心对称
- 4.4 平行四边形的判定
- 4.5 三角形的中位线
- 4.6 反证法
- 第五章 特殊平行四边形
- 5.1 矩形
- 5.2 菱形
- 5.3 正方形
- 第六章 反比例函数
- 6.1 反比例函数
- 6.2 反比例函数的图象和性质
- 6.3 反比例函数的应用
