第一章 二次根式 单元提高检测卷(含答案)
文档属性
| 名称 | 第一章 二次根式 单元提高检测卷(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 66.8KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-21 14:36:32 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
2021-2022学年浙教版数学8年级下学期
第一章二次根式提高检测卷
一、单选题
1.下列计算正确的是( )
A. B.
C. D.
2.式子有意义,则实数a的取值范围是( )
A.a≥2 B.a≠5 C.a≥2且a≠5 D.a>2且a≠5
3.若1≤x≤4,化简 的结果为( )
A.3 B.2x﹣5 C.﹣3 D.5﹣2x
4.当时,化简二次根式,结果正确的是( )
A. B. C. D.
5.若最简二次根式与最简二次根式是同类二次根式,则a的值是( )
A.a=1 B.a=-1 C.a=2 D.a=-2
6.把代数式 中的 移到根号内,那么这个代数式等于( )
A. B. C. D.
7.实数 , 在数轴上对应的点的位置如图所示那么 化简的结果( )
A. B. C. D.
8.下列四个算式,其中一定成立的是( )
① =a2+1;② =a;③ = (ab>0);④
A.①②③④ B.①②③ C.①③ D.①
9.若实数x,y满足y= ﹣2020,则4x﹣y的值为( )
A.2021 B.2022 C.2023 D.2024
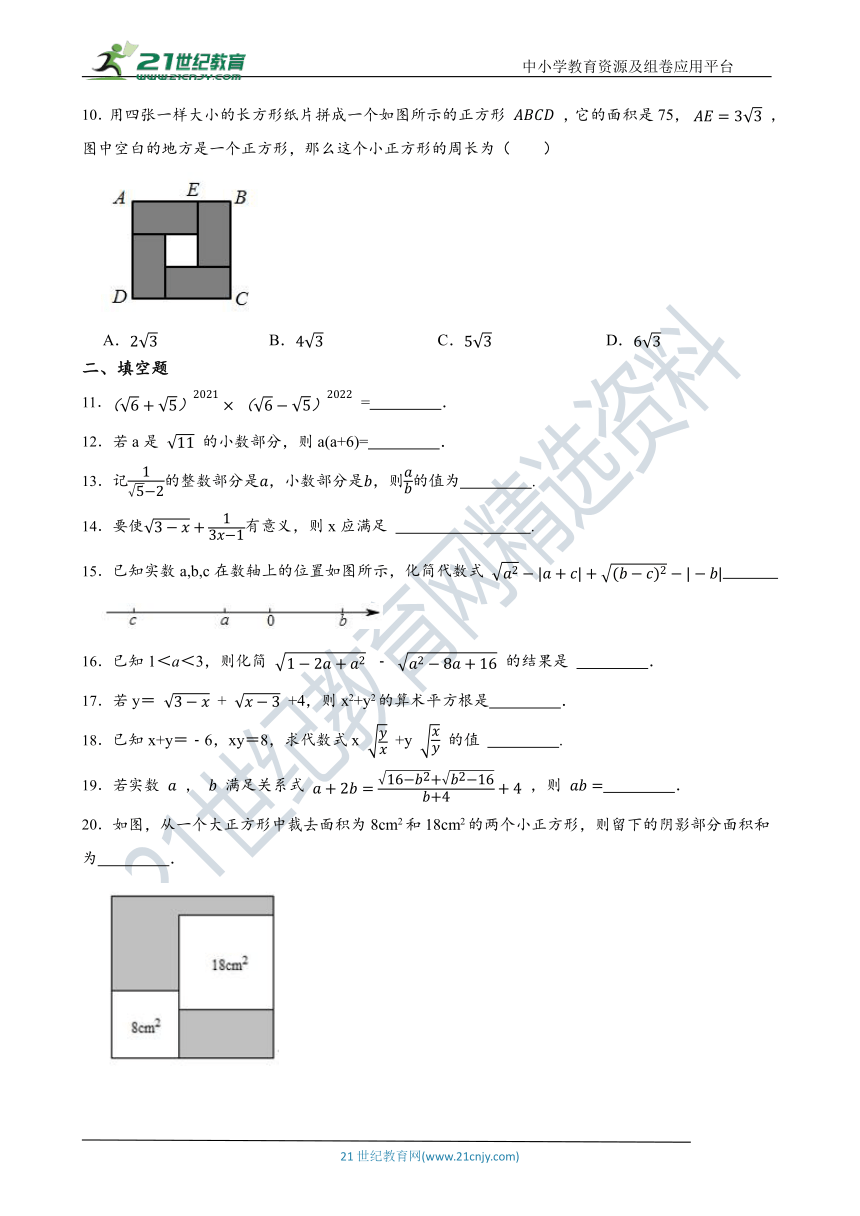
10.用四张一样大小的长方形纸片拼成一个如图所示的正方形 ,它的面积是75, ,图中空白的地方是一个正方形,那么这个小正方形的周长为( )
A. B. C. D.
二、填空题
11. = .
12.若a是 的小数部分,则a(a+6)= .
13.记的整数部分是,小数部分是,则的值为 .
14.要使有意义,则x应满足 .
15.已知实数a,b,c在数轴上的位置如图所示,化简代数式
16.已知1<a<3,则化简 ﹣ 的结果是 .
17.若y= + +4,则x2+y2的算术平方根是 .
18.已知x+y=﹣6,xy=8,求代数式x +y 的值 .
19.若实数 , 满足关系式 ,则 .
20.如图,从一个大正方形中裁去面积为8cm2和18cm2的两个小正方形,则留下的阴影部分面积和为 .
三、计算题
21.计算:
(1)
(2).
22.
(1)
(2)
四、综合题
23.
(1)在Rt△ABC中,∠C=Rt∠,AC=2 ,AB=3 ,求Rt△ABC的周长和面积.
(2)已知a= ,b= ,求a2﹣ab+b2的值.
24.已知.
(1)求的值;
(2)求的平方根.
25.已知: , (n为正整数).
(1)求 的值(结果用含n的代数式表示);
(2)若(1)中代数式的值是整数,求正整数n的最小值.
26.若关于x、y的二元一次方程组 的解满足
(1)求a的值;
(2)m为任意实数,当m为何值时, 有最小值?求出这个最小值.
27.阅读下面问题:
阅读理解:
﹣1;
;
.
应用计算:
(1) 的值;
(2) (n为正整数)的值.
(3) 的值.
28.阅读材料:
黑白双雄、纵横江湖;双剑合璧、天下无敌.这是武侠小说中的常见描述,其意是指两个人合在一起,取长补短,威力无比.
在二次根式中也有这种相辅相成的“对子”.如: , ,它们的积不含根号,我们说这两个二次根式互为有理化因式,其中一个是另一个的有理化因式,于是,二次根式除法可以这样理解:如: , .像这样,通过分子、分母同乘以一个式子把分母中的根号化去或把根号中的分母化去,叫做分母有理化.
解决问题:
(1) 的有理化因式可以是 , 分母有理化得 .
(2)计算:
①已知 , ,求 的值;
② .
答案解析部分
1.【答案】D
2.【答案】C
3.【答案】B
4.【答案】D
5.【答案】A
6.【答案】A
7.【答案】C
8.【答案】D
9.【答案】B
10.【答案】B
11.【答案】
12.【答案】2
13.【答案】
14.【答案】x≤3且
15.【答案】0
16.【答案】2a 5
17.【答案】5
18.【答案】
19.【答案】-16
20.【答案】24cm2
21.【答案】(1)解:原式
.
(2)解:原式
.
22.【答案】(1)解:原式,
,
,
;
(2)解:原式,
,
.
23.【答案】(1)解:如图,
∵ ∠C=Rt∠,AC=2 ,AB=3 ,
∴,
∴△ABC的周长为;
∴;
(2)解:, ,
a2﹣ab+b2=(a+b)2-3ab=.
24.【答案】(1)解:由题意可得:,解得:
(2)解:将代入可得:,解得:,
可得,
所以的平方根为.
25.【答案】(1)解:∵ , ,
∴ , ,
则 ;
(2)解:∵ 为整数,即 为整数,
∴ 应为完全平方数,
∵ 为正整数,
∴当 时, 为满足题意的最小值.
26.【答案】(1)解: ,
①②得: ,
,
,
,解得
(2)解: 时, ,
当 ,即 时, 有最小值,最小值为2
27.【答案】(1)解:
(2)解:
归纳拓展:
(3)解: ,
,
= + + + ,
= ,
=10-1,
=9.
28.【答案】(1);
(2)解:①当 ,
时,
.
②原式
.
21世纪教育网(www.21cnjy.com)
2021-2022学年浙教版数学8年级下学期
第一章二次根式提高检测卷
一、单选题
1.下列计算正确的是( )
A. B.
C. D.
2.式子有意义,则实数a的取值范围是( )
A.a≥2 B.a≠5 C.a≥2且a≠5 D.a>2且a≠5
3.若1≤x≤4,化简 的结果为( )
A.3 B.2x﹣5 C.﹣3 D.5﹣2x
4.当时,化简二次根式,结果正确的是( )
A. B. C. D.
5.若最简二次根式与最简二次根式是同类二次根式,则a的值是( )
A.a=1 B.a=-1 C.a=2 D.a=-2
6.把代数式 中的 移到根号内,那么这个代数式等于( )
A. B. C. D.
7.实数 , 在数轴上对应的点的位置如图所示那么 化简的结果( )
A. B. C. D.
8.下列四个算式,其中一定成立的是( )
① =a2+1;② =a;③ = (ab>0);④
A.①②③④ B.①②③ C.①③ D.①
9.若实数x,y满足y= ﹣2020,则4x﹣y的值为( )
A.2021 B.2022 C.2023 D.2024
10.用四张一样大小的长方形纸片拼成一个如图所示的正方形 ,它的面积是75, ,图中空白的地方是一个正方形,那么这个小正方形的周长为( )
A. B. C. D.
二、填空题
11. = .
12.若a是 的小数部分,则a(a+6)= .
13.记的整数部分是,小数部分是,则的值为 .
14.要使有意义,则x应满足 .
15.已知实数a,b,c在数轴上的位置如图所示,化简代数式
16.已知1<a<3,则化简 ﹣ 的结果是 .
17.若y= + +4,则x2+y2的算术平方根是 .
18.已知x+y=﹣6,xy=8,求代数式x +y 的值 .
19.若实数 , 满足关系式 ,则 .
20.如图,从一个大正方形中裁去面积为8cm2和18cm2的两个小正方形,则留下的阴影部分面积和为 .
三、计算题
21.计算:
(1)
(2).
22.
(1)
(2)
四、综合题
23.
(1)在Rt△ABC中,∠C=Rt∠,AC=2 ,AB=3 ,求Rt△ABC的周长和面积.
(2)已知a= ,b= ,求a2﹣ab+b2的值.
24.已知.
(1)求的值;
(2)求的平方根.
25.已知: , (n为正整数).
(1)求 的值(结果用含n的代数式表示);
(2)若(1)中代数式的值是整数,求正整数n的最小值.
26.若关于x、y的二元一次方程组 的解满足
(1)求a的值;
(2)m为任意实数,当m为何值时, 有最小值?求出这个最小值.
27.阅读下面问题:
阅读理解:
﹣1;
;
.
应用计算:
(1) 的值;
(2) (n为正整数)的值.
(3) 的值.
28.阅读材料:
黑白双雄、纵横江湖;双剑合璧、天下无敌.这是武侠小说中的常见描述,其意是指两个人合在一起,取长补短,威力无比.
在二次根式中也有这种相辅相成的“对子”.如: , ,它们的积不含根号,我们说这两个二次根式互为有理化因式,其中一个是另一个的有理化因式,于是,二次根式除法可以这样理解:如: , .像这样,通过分子、分母同乘以一个式子把分母中的根号化去或把根号中的分母化去,叫做分母有理化.
解决问题:
(1) 的有理化因式可以是 , 分母有理化得 .
(2)计算:
①已知 , ,求 的值;
② .
答案解析部分
1.【答案】D
2.【答案】C
3.【答案】B
4.【答案】D
5.【答案】A
6.【答案】A
7.【答案】C
8.【答案】D
9.【答案】B
10.【答案】B
11.【答案】
12.【答案】2
13.【答案】
14.【答案】x≤3且
15.【答案】0
16.【答案】2a 5
17.【答案】5
18.【答案】
19.【答案】-16
20.【答案】24cm2
21.【答案】(1)解:原式
.
(2)解:原式
.
22.【答案】(1)解:原式,
,
,
;
(2)解:原式,
,
.
23.【答案】(1)解:如图,
∵ ∠C=Rt∠,AC=2 ,AB=3 ,
∴,
∴△ABC的周长为;
∴;
(2)解:, ,
a2﹣ab+b2=(a+b)2-3ab=.
24.【答案】(1)解:由题意可得:,解得:
(2)解:将代入可得:,解得:,
可得,
所以的平方根为.
25.【答案】(1)解:∵ , ,
∴ , ,
则 ;
(2)解:∵ 为整数,即 为整数,
∴ 应为完全平方数,
∵ 为正整数,
∴当 时, 为满足题意的最小值.
26.【答案】(1)解: ,
①②得: ,
,
,
,解得
(2)解: 时, ,
当 ,即 时, 有最小值,最小值为2
27.【答案】(1)解:
(2)解:
归纳拓展:
(3)解: ,
,
= + + + ,
= ,
=10-1,
=9.
28.【答案】(1);
(2)解:①当 ,
时,
.
②原式
.
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第一章 二次根式
- 1.1 二次根式
- 1.2 二次根式的性质
- 1.3 二次根式的运算
- 第二章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程的应用
- 2.4 一元二次方程根与系数的关系(选学)
- 第三章 数据分析初步
- 3.1 平均数
- 3.2 中位数和众数
- 3.3 方差和标准差
- 第四章 平行四边形
- 4.1 多边形
- 4.2 平行四边形
- 4.3 中心对称
- 4.4 平行四边形的判定
- 4.5 三角形的中位线
- 4.6 反证法
- 第五章 特殊平行四边形
- 5.1 矩形
- 5.2 菱形
- 5.3 正方形
- 第六章 反比例函数
- 6.1 反比例函数
- 6.2 反比例函数的图象和性质
- 6.3 反比例函数的应用
