第五章《特殊平行四边形》单元综合提高测试(含答案)
文档属性
| 名称 | 第五章《特殊平行四边形》单元综合提高测试(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-24 10:49:57 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
第五章 特殊平行四边形
综合提高测试
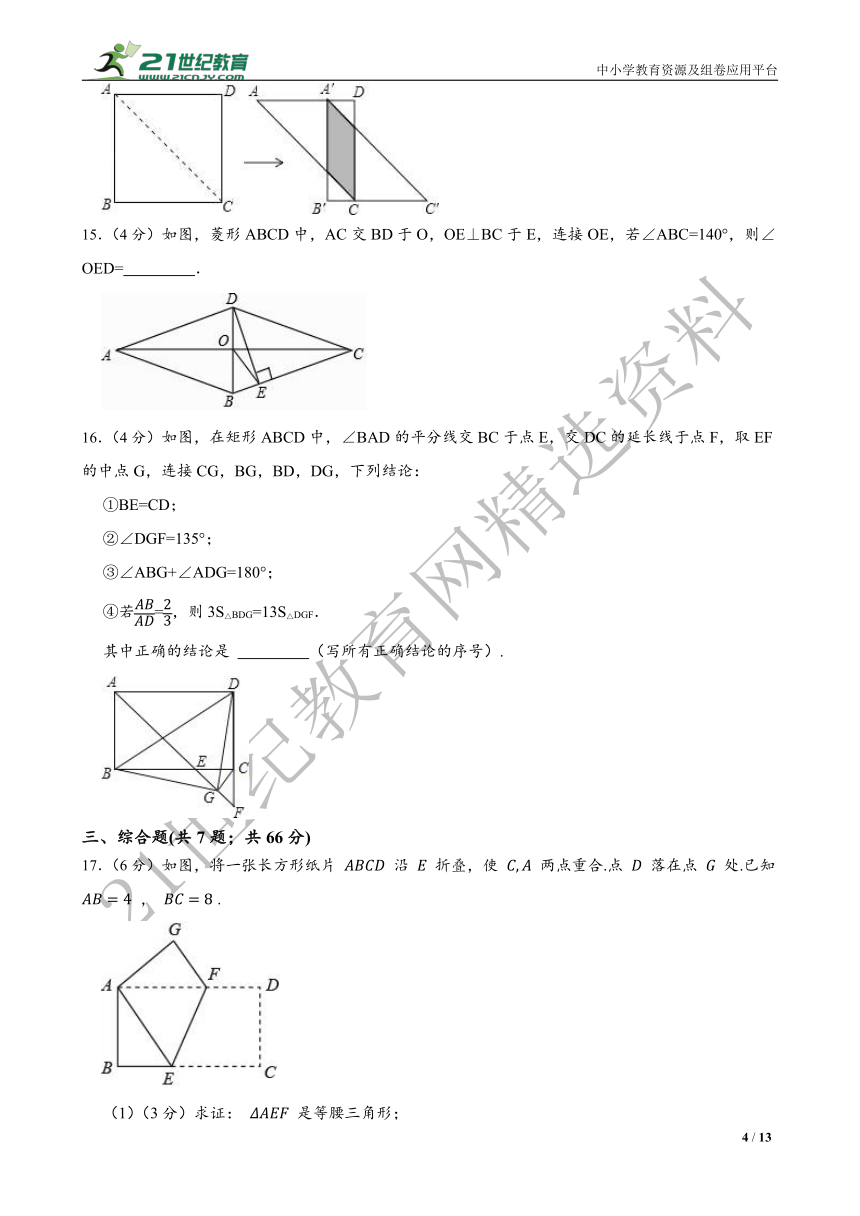
一、单选题(共10题;共30分)
1.(3分)下列说法正确的是( )
A.一组对边平行,另一组对边相等的四边形是平行四边形
B.对角线相等的平行四边形是菱形
C.三个角都是直角的四边形是矩形
D.一组邻边相等的平行四边形是正方形
2.(3分)如图,把矩形 沿 对折后使两部分重合,若 ,则 =( )
A.110° B.115° C.120° D.130°
3.(3分)边长为5的菱形ABCD按如图所示放置在数轴上,其中A点表示数﹣2,C点表示数6,则BD=( )
A.4 B.6 C.8 D.10
4.(3分)如图,在矩形 中,两条对角线 与 相交于点 , , ,则 的长为( )
A.5 B. C. D.
5.(3分)将矩形纸片ABCD按如图所示的方式折叠,恰好得到菱形AECF.若AB=3,则菱形AECF的面积为( )
A.1 B. C. D.4
6.(3分)有3个正方形如图所示放置,阴影部分的面积依次记为S1,S2,则S1:S2等于( )
A.1: B.1:2 C.2:3 D.4:9
7.(3分)如图,正方形ABCD中,点E、F、H分别是AB、BC、CD的中点,CE、DF交于G,连接AG、HG.下列结论:①CE⊥DF;②AG=AD;③∠CHG=∠DAG;④HG= AD.其中正确的有( )
A.1个 B.2个 C.3个 D.4个
8.(3分)如图,在Rt△ABC中,∠B=90°,AC=120cm,∠A=60°,点D从点C出发沿
CA方向以4cm/秒的速度向点A匀速运动,同时点E从点A出发沿AB方向以2cm/秒的速度向点B匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点D、E运动的时间是t秒.过点D作DF⊥BC于点F,连接DE,EF.当四边形AEFD是菱形时,t的值为( )
A.20秒 B.18秒 C.12秒 D.6秒
9.(3分)如图1,在矩形MNPO中,动点R从点N出发,沿N→P→O→M方向运动至点M处停止.设点R运动的路程为x,△MNR的面积为y,如果y关于x的函数图象如图2所示,则矩形MNPO的周长是( )
A.11 B.15 C.16 D.24
10.(3分)如图,矩形ABCD的面积为1cm2,对角线交于点O;以AB、AO为邻边作平行四边形AOC1B,对角线交于点O1;以AB、AO1为邻边作平行四边形AO1C2B…;依此类推,则平行四边形AO2014C2015B的面积为( )
A. B. C. D.
二、填空题(共6题;共24分)
11.(4分)菱形的周长为12,它的一个内角为60°,则菱形的较短的对角线长为 .
12.(4分)如图,矩形ABCD中,AB=3,BC=4,则图中五个小矩形的周长之和为 .
13.(4分)如图,点P是正方形ABCD内位于对角线AC下方的一点,∠1=∠2,则∠BPC的度数为 °.
14.(4分)如图,将边长为12的正方形ABCD沿其对角线AC剪开,再把△ABC沿着AD方向平移,得到△A′B′C′,当两个三角形重叠部分的面积为32时,它移动的距离AA′等于 .
15.(4分)如图,菱形ABCD中,AC交BD于O,OE⊥BC于E,连接OE,若∠ABC=140°,则∠OED= .
16.(4分)如图,在矩形ABCD中,∠BAD的平分线交BC于点E,交DC的延长线于点F,取EF的中点G,连接CG,BG,BD,DG,下列结论:
①BE=CD;
②∠DGF=135°;
③∠ABG+∠ADG=180°;
④若=,则3S△BDG=13S△DGF.
其中正确的结论是 (写所有正确结论的序号).
三、综合题(共7题;共66分)
17.(6分)如图,将一张长方形纸片 沿 折叠,使 两点重合.点 落在点 处.已知 , .
(1)(3分)求证: 是等腰三角形;
(2)(3分)求线段 的长.
18.(6分)如图,在四边形ABCD中,AB∥DC,AB=AD,对角线AC,BD相交于点O,AC平分∠BAD,过点C作CE⊥AB交AB的延长线于点E,连接OE.
(1)(3分)求证:四边形ABCD是菱形;
(2)(3分)若AB= ,BD=2,求OE的长.
19.(8分)如图,已知在△ABC中,D,E,F分别是AB,BC,AC的中点,连结DF,EF,BF.
(1)(4分)求证:四边形BEFD是平行四边形;
(2)(4分)若∠AFB=90°,AB=6,求四边形BEFD的周长.
20.(8分)如图,点P是∠AOB内的一点,过点P作PC∥OB,PD∥OA,分别交OA、OB于点C、D,且PE⊥OA,PF⊥OB,垂足分别为点E、F.
(1)(4分)求证:OC CE=OD DF;
(2)(4分)当点P位于∠AOB的什么位置时,四边形CODP是菱形并证明你的结论.
21.(12分)在矩形ABCD中,∠DAB的平分线交BC于点E,交DC的延长线于点F,连接BD.
(1)(3分)计算∠AEC的度数;
(2)(4分)求证:BE=DC;
(3)(5分)点P是线段EF上一动点(不与点E,F重合),在点P运动过程中,能否使△BDP成为等腰直角三角形?若能,写出点P满足的条件并证明;若不能,请说明理由.
22.(12分)如图,正方形ABCD中,AB=4,P是CD边上的动点(P点不与C、D重合),过点P作直线与BC的延长线交于点E,与AD交于点F,且CP=CE,连接DE、BP、BF,设CP═x,△PBF的面积为S1,△PDE的面积为S2.
(1)(3分)求证:BP⊥DE.
(2)(4分)求S1﹣S2关于x的函数解析式,并写出x的取值范围.
(3)(5分)分别求当∠PBF=30°和∠PBF=45°时,S1﹣S2的值.
23.(14分)如图1,四边形ABCD是菱形,AD=5,过点D作AB的垂线DH,垂足为H,交对角线AC于M,连接BM,且AH=3.
(1)(3分)求证:DM=BM;
(2)(3分)求MH的长;
(3)(4分)如图2,动点P从点A出发,沿折线ABC方向以2个单位/秒的速度向终点C匀速运动,设△PMB的面积为S(S≠0),点P的运动时间为t秒,求S与t之间的函数关系式;
(4)(4分)在(3)的条件下,当点P在边AB上运动时是否存在这样的 t值,使∠MPB与 ∠BCD互为余角,若存在,则求出t值,若不存,在请说明理由.
答案解析部分
1.【答案】C
2.【答案】B
3.【答案】B
4.【答案】D
5.【答案】C
6.【答案】D
7.【答案】D
8.【答案】A
9.【答案】C
10.【答案】C
11.【答案】3
12.【答案】14
13.【答案】135
14.【答案】4或8
15.【答案】20°
16.【答案】①③④
17.【答案】(1)证明: 四边形 是矩形
因为折叠,则
是等腰三角形
(2)解: 四边形 是矩形
,
设 ,则
因为折叠,则 , ,
在 中
即
解得:
18.【答案】(1)证明:∵AB∥DC,
∴∠DCA=∠CAB,
∵AC平分∠BAD,
∴∠CAB=∠DAC
∴∠DCA=∠DAC,
∴AD=DC
同理得:AD=AB,
∴AB=CD
∴四边形ABCD是平行四边形
∵AB=AD
∴四边形ABCD是菱形。
(2)解:∵四边形ABCD是菱形,
∴AC⊥BD,且AC与BD互相平分,
∵BD=2BO=2,∴BO=1
∵AO=
∴AO=2,
∴AC=2AO=4
∵CE⊥AB,
∴∠CEA=90°,AO=CO,
∴OE==2
19.【答案】(1)证明:∵D,E,F分别是AB,BC,AC的中点,
∴DF∥BC,FE∥AB, ∴四边形BEFD是平行四边形
(2)解:∵∠AFB=90°,D是AB的中点,AB=6, ∴DF=DB=DA= AB=3.
∴四边形BEFD是菱形.
∵DB=3, ∴四边形BEFD的周长为12.
20.【答案】(1)证明:(1)∵PC∥OB,PD∥OA,
∴四边形OCPD是平行四边形,且∠ECP=∠O,∠FDP=∠O.
∴PC=OD,PD=OC,∠ECP=∠FDP.
∵PE⊥OA,PF⊥OB,
∴∠PEC=∠PFD=90°.
∴△PCE∽△PDF.
∴.
即得.
∴OC CE=OD DF.
(2)当点P在∠AOB的平分线上时,四边形CODP是菱形.
∵当点P在∠AOB的平分线上时,由PE⊥OA,PF⊥OB,得PE=PF,
∴由△PCE∽△PDF,得,即得PC=PD.
∵四边形CODP是平行四边形,
∴四边形CODP是菱形.
当点P不在∠AOB的平分线上时,可得PE≠PF.即得PC≠PD.
∴当点P不在∠AOB的平分线上时,四边形CODP不是菱形.
21.【答案】(1)解:∵四边形ABCD时矩形,
∴∠DAB=∠ABC=∠DCB=90°,
∵∠DAB的平分线交BC于点E,
∴∠BAE=∠EAD=45°,
∴∠AEC=∠ABC+∠BAE=90°+45°=135°
(2)证明:∵四边形ABCD是矩形,
∴∠DAB=∠DCB=90°,AB∥DC,AD∥BC,AB=DC.
∴∠BEA=∠FAD.
∵AF是∠DAB的平分线,
∴∠FAB=∠FAD=45°.
∴∠FAB=∠BEA=45°.
∴AB=BF.
∴BE=DC
(3)解:在点P运动过程中,能使△BDP成为等腰直角三角形,此时点P是线段EF的中点.理由如下:在△ECF中,∠ECF=90°,∠FEC=∠AEB=45°,∴∠F=90°﹣∠FEC=90°﹣45°=45°.∴∠F=∠FEC.∴CE=CF.∵点P是线段EF的中点,∴EP=CP,∠ECP=45°,∠EPC=90°.∴∠DCP=∠DCB+∠ECP=90°+45°=135°.∵∠BEP=∠AEC=135°,∴∠BEP=∠DCP.
在△BEP和△DCP中, ,
∴△BEP≌△DCP(SAS),
∴BP=DP,∠BPE=∠DPC.∴∠BPD=∠BPE+∠DPE=∠DPC+∠DPE=∠EPC=90°.∴△BDP为等腰直角三角形
22.【答案】(1)解:如图1中,延长BP交DE于M.
∵四边形ABCD是正方形,
∴CB=CD,∠BCP=∠DCE=90°,
∵CP=CE,
∴△BCP≌△DCE,
∴∠BCP=∠CDE,
∵∠CBP+∠CPB=90°,∠CPB=∠DPM,
∴∠CDE+∠DPM=90°,
∴∠DMP=90°,
∴BP⊥DE.
(2)解:由题意S1﹣S2= (4+x) x﹣ (4﹣x) x=x2(0<x<4).
(3)解:①如图2中,当∠PBF=30°时,∵∠CPE=∠CEP=∠DPF=45°,∠FDP=90°,∴∠PFD=∠DPF=45°,∴DF=DP,∵AD=CD,∴AF=PC,∵AB=BC,∠A=∠BCP=90°,∴△BAF≌△BCP,∴∠ABF=∠CBP=30°,∴x=PC=BC tan30°= ,∴S1﹣S2=x2= .
②如图3中,当∠PBF=45°时,在CB上截取CN=CP,理解PN.
由①可知△ABF≌△BCP,∴∠ABF=∠CBP,∵∠PBF=45°,∴∠CBP=22.5°,
∵∠CNP=∠NBP+∠NPB=45°,
∴∠NBP=∠NPB=22.5°,∴BN=PN= x,∴ x+x=4,∴x=4 ﹣4,∴S1﹣S2=(4 ﹣4)2=48﹣32 .
23.【答案】(1)证明:∵AC是菱形ABCD的对角线,∴∠ACD=∠ACB,CD=CB,在△DCM和△BCM中,
∴△DCM≌△BCM, ∴DM=BM
(2)解:设BM=x,在Rt△BHM中,BM=DM=x,HM=DH DM=4 x,BH=AB AH=2,
根据勾股定理得,BM2=MH2+BH2x2=(4 x)2+22解之:x=∴HM=4-=
(3)解:在△BCM和△DCM中,
∴△BCM≌△DCM,∴BM=DM=,∠CDM=∠CBM=90
① 当P在AB之间时,S=(5 2t)×= t+;②当P在BC之间时S=(2t 5)×=t
(4)存在,∵∠ADM+∠BAD=90 ,∠BCD=∠BAD,∴∠ADM+∠BCD=90 ,
∵∠MPB+∠BCD=90 ,∴∠MPB=∠ADM,
∵四边形ABCD是菱形,∴∠DAM=∠BAM,
∵AM=AM,∴△ADM≌△ABM,∴∠ADM=∠ABM,∴∠MPB=∠ABM,
∵MH⊥AB,∴PH=BH=2,∴BP=2BH=4,
∵AB=5,∴AP=1,∴t==
1 / 1
第五章 特殊平行四边形
综合提高测试
一、单选题(共10题;共30分)
1.(3分)下列说法正确的是( )
A.一组对边平行,另一组对边相等的四边形是平行四边形
B.对角线相等的平行四边形是菱形
C.三个角都是直角的四边形是矩形
D.一组邻边相等的平行四边形是正方形
2.(3分)如图,把矩形 沿 对折后使两部分重合,若 ,则 =( )
A.110° B.115° C.120° D.130°
3.(3分)边长为5的菱形ABCD按如图所示放置在数轴上,其中A点表示数﹣2,C点表示数6,则BD=( )
A.4 B.6 C.8 D.10
4.(3分)如图,在矩形 中,两条对角线 与 相交于点 , , ,则 的长为( )
A.5 B. C. D.
5.(3分)将矩形纸片ABCD按如图所示的方式折叠,恰好得到菱形AECF.若AB=3,则菱形AECF的面积为( )
A.1 B. C. D.4
6.(3分)有3个正方形如图所示放置,阴影部分的面积依次记为S1,S2,则S1:S2等于( )
A.1: B.1:2 C.2:3 D.4:9
7.(3分)如图,正方形ABCD中,点E、F、H分别是AB、BC、CD的中点,CE、DF交于G,连接AG、HG.下列结论:①CE⊥DF;②AG=AD;③∠CHG=∠DAG;④HG= AD.其中正确的有( )
A.1个 B.2个 C.3个 D.4个
8.(3分)如图,在Rt△ABC中,∠B=90°,AC=120cm,∠A=60°,点D从点C出发沿
CA方向以4cm/秒的速度向点A匀速运动,同时点E从点A出发沿AB方向以2cm/秒的速度向点B匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点D、E运动的时间是t秒.过点D作DF⊥BC于点F,连接DE,EF.当四边形AEFD是菱形时,t的值为( )
A.20秒 B.18秒 C.12秒 D.6秒
9.(3分)如图1,在矩形MNPO中,动点R从点N出发,沿N→P→O→M方向运动至点M处停止.设点R运动的路程为x,△MNR的面积为y,如果y关于x的函数图象如图2所示,则矩形MNPO的周长是( )
A.11 B.15 C.16 D.24
10.(3分)如图,矩形ABCD的面积为1cm2,对角线交于点O;以AB、AO为邻边作平行四边形AOC1B,对角线交于点O1;以AB、AO1为邻边作平行四边形AO1C2B…;依此类推,则平行四边形AO2014C2015B的面积为( )
A. B. C. D.
二、填空题(共6题;共24分)
11.(4分)菱形的周长为12,它的一个内角为60°,则菱形的较短的对角线长为 .
12.(4分)如图,矩形ABCD中,AB=3,BC=4,则图中五个小矩形的周长之和为 .
13.(4分)如图,点P是正方形ABCD内位于对角线AC下方的一点,∠1=∠2,则∠BPC的度数为 °.
14.(4分)如图,将边长为12的正方形ABCD沿其对角线AC剪开,再把△ABC沿着AD方向平移,得到△A′B′C′,当两个三角形重叠部分的面积为32时,它移动的距离AA′等于 .
15.(4分)如图,菱形ABCD中,AC交BD于O,OE⊥BC于E,连接OE,若∠ABC=140°,则∠OED= .
16.(4分)如图,在矩形ABCD中,∠BAD的平分线交BC于点E,交DC的延长线于点F,取EF的中点G,连接CG,BG,BD,DG,下列结论:
①BE=CD;
②∠DGF=135°;
③∠ABG+∠ADG=180°;
④若=,则3S△BDG=13S△DGF.
其中正确的结论是 (写所有正确结论的序号).
三、综合题(共7题;共66分)
17.(6分)如图,将一张长方形纸片 沿 折叠,使 两点重合.点 落在点 处.已知 , .
(1)(3分)求证: 是等腰三角形;
(2)(3分)求线段 的长.
18.(6分)如图,在四边形ABCD中,AB∥DC,AB=AD,对角线AC,BD相交于点O,AC平分∠BAD,过点C作CE⊥AB交AB的延长线于点E,连接OE.
(1)(3分)求证:四边形ABCD是菱形;
(2)(3分)若AB= ,BD=2,求OE的长.
19.(8分)如图,已知在△ABC中,D,E,F分别是AB,BC,AC的中点,连结DF,EF,BF.
(1)(4分)求证:四边形BEFD是平行四边形;
(2)(4分)若∠AFB=90°,AB=6,求四边形BEFD的周长.
20.(8分)如图,点P是∠AOB内的一点,过点P作PC∥OB,PD∥OA,分别交OA、OB于点C、D,且PE⊥OA,PF⊥OB,垂足分别为点E、F.
(1)(4分)求证:OC CE=OD DF;
(2)(4分)当点P位于∠AOB的什么位置时,四边形CODP是菱形并证明你的结论.
21.(12分)在矩形ABCD中,∠DAB的平分线交BC于点E,交DC的延长线于点F,连接BD.
(1)(3分)计算∠AEC的度数;
(2)(4分)求证:BE=DC;
(3)(5分)点P是线段EF上一动点(不与点E,F重合),在点P运动过程中,能否使△BDP成为等腰直角三角形?若能,写出点P满足的条件并证明;若不能,请说明理由.
22.(12分)如图,正方形ABCD中,AB=4,P是CD边上的动点(P点不与C、D重合),过点P作直线与BC的延长线交于点E,与AD交于点F,且CP=CE,连接DE、BP、BF,设CP═x,△PBF的面积为S1,△PDE的面积为S2.
(1)(3分)求证:BP⊥DE.
(2)(4分)求S1﹣S2关于x的函数解析式,并写出x的取值范围.
(3)(5分)分别求当∠PBF=30°和∠PBF=45°时,S1﹣S2的值.
23.(14分)如图1,四边形ABCD是菱形,AD=5,过点D作AB的垂线DH,垂足为H,交对角线AC于M,连接BM,且AH=3.
(1)(3分)求证:DM=BM;
(2)(3分)求MH的长;
(3)(4分)如图2,动点P从点A出发,沿折线ABC方向以2个单位/秒的速度向终点C匀速运动,设△PMB的面积为S(S≠0),点P的运动时间为t秒,求S与t之间的函数关系式;
(4)(4分)在(3)的条件下,当点P在边AB上运动时是否存在这样的 t值,使∠MPB与 ∠BCD互为余角,若存在,则求出t值,若不存,在请说明理由.
答案解析部分
1.【答案】C
2.【答案】B
3.【答案】B
4.【答案】D
5.【答案】C
6.【答案】D
7.【答案】D
8.【答案】A
9.【答案】C
10.【答案】C
11.【答案】3
12.【答案】14
13.【答案】135
14.【答案】4或8
15.【答案】20°
16.【答案】①③④
17.【答案】(1)证明: 四边形 是矩形
因为折叠,则
是等腰三角形
(2)解: 四边形 是矩形
,
设 ,则
因为折叠,则 , ,
在 中
即
解得:
18.【答案】(1)证明:∵AB∥DC,
∴∠DCA=∠CAB,
∵AC平分∠BAD,
∴∠CAB=∠DAC
∴∠DCA=∠DAC,
∴AD=DC
同理得:AD=AB,
∴AB=CD
∴四边形ABCD是平行四边形
∵AB=AD
∴四边形ABCD是菱形。
(2)解:∵四边形ABCD是菱形,
∴AC⊥BD,且AC与BD互相平分,
∵BD=2BO=2,∴BO=1
∵AO=
∴AO=2,
∴AC=2AO=4
∵CE⊥AB,
∴∠CEA=90°,AO=CO,
∴OE==2
19.【答案】(1)证明:∵D,E,F分别是AB,BC,AC的中点,
∴DF∥BC,FE∥AB, ∴四边形BEFD是平行四边形
(2)解:∵∠AFB=90°,D是AB的中点,AB=6, ∴DF=DB=DA= AB=3.
∴四边形BEFD是菱形.
∵DB=3, ∴四边形BEFD的周长为12.
20.【答案】(1)证明:(1)∵PC∥OB,PD∥OA,
∴四边形OCPD是平行四边形,且∠ECP=∠O,∠FDP=∠O.
∴PC=OD,PD=OC,∠ECP=∠FDP.
∵PE⊥OA,PF⊥OB,
∴∠PEC=∠PFD=90°.
∴△PCE∽△PDF.
∴.
即得.
∴OC CE=OD DF.
(2)当点P在∠AOB的平分线上时,四边形CODP是菱形.
∵当点P在∠AOB的平分线上时,由PE⊥OA,PF⊥OB,得PE=PF,
∴由△PCE∽△PDF,得,即得PC=PD.
∵四边形CODP是平行四边形,
∴四边形CODP是菱形.
当点P不在∠AOB的平分线上时,可得PE≠PF.即得PC≠PD.
∴当点P不在∠AOB的平分线上时,四边形CODP不是菱形.
21.【答案】(1)解:∵四边形ABCD时矩形,
∴∠DAB=∠ABC=∠DCB=90°,
∵∠DAB的平分线交BC于点E,
∴∠BAE=∠EAD=45°,
∴∠AEC=∠ABC+∠BAE=90°+45°=135°
(2)证明:∵四边形ABCD是矩形,
∴∠DAB=∠DCB=90°,AB∥DC,AD∥BC,AB=DC.
∴∠BEA=∠FAD.
∵AF是∠DAB的平分线,
∴∠FAB=∠FAD=45°.
∴∠FAB=∠BEA=45°.
∴AB=BF.
∴BE=DC
(3)解:在点P运动过程中,能使△BDP成为等腰直角三角形,此时点P是线段EF的中点.理由如下:在△ECF中,∠ECF=90°,∠FEC=∠AEB=45°,∴∠F=90°﹣∠FEC=90°﹣45°=45°.∴∠F=∠FEC.∴CE=CF.∵点P是线段EF的中点,∴EP=CP,∠ECP=45°,∠EPC=90°.∴∠DCP=∠DCB+∠ECP=90°+45°=135°.∵∠BEP=∠AEC=135°,∴∠BEP=∠DCP.
在△BEP和△DCP中, ,
∴△BEP≌△DCP(SAS),
∴BP=DP,∠BPE=∠DPC.∴∠BPD=∠BPE+∠DPE=∠DPC+∠DPE=∠EPC=90°.∴△BDP为等腰直角三角形
22.【答案】(1)解:如图1中,延长BP交DE于M.
∵四边形ABCD是正方形,
∴CB=CD,∠BCP=∠DCE=90°,
∵CP=CE,
∴△BCP≌△DCE,
∴∠BCP=∠CDE,
∵∠CBP+∠CPB=90°,∠CPB=∠DPM,
∴∠CDE+∠DPM=90°,
∴∠DMP=90°,
∴BP⊥DE.
(2)解:由题意S1﹣S2= (4+x) x﹣ (4﹣x) x=x2(0<x<4).
(3)解:①如图2中,当∠PBF=30°时,∵∠CPE=∠CEP=∠DPF=45°,∠FDP=90°,∴∠PFD=∠DPF=45°,∴DF=DP,∵AD=CD,∴AF=PC,∵AB=BC,∠A=∠BCP=90°,∴△BAF≌△BCP,∴∠ABF=∠CBP=30°,∴x=PC=BC tan30°= ,∴S1﹣S2=x2= .
②如图3中,当∠PBF=45°时,在CB上截取CN=CP,理解PN.
由①可知△ABF≌△BCP,∴∠ABF=∠CBP,∵∠PBF=45°,∴∠CBP=22.5°,
∵∠CNP=∠NBP+∠NPB=45°,
∴∠NBP=∠NPB=22.5°,∴BN=PN= x,∴ x+x=4,∴x=4 ﹣4,∴S1﹣S2=(4 ﹣4)2=48﹣32 .
23.【答案】(1)证明:∵AC是菱形ABCD的对角线,∴∠ACD=∠ACB,CD=CB,在△DCM和△BCM中,
∴△DCM≌△BCM, ∴DM=BM
(2)解:设BM=x,在Rt△BHM中,BM=DM=x,HM=DH DM=4 x,BH=AB AH=2,
根据勾股定理得,BM2=MH2+BH2x2=(4 x)2+22解之:x=∴HM=4-=
(3)解:在△BCM和△DCM中,
∴△BCM≌△DCM,∴BM=DM=,∠CDM=∠CBM=90
① 当P在AB之间时,S=(5 2t)×= t+;②当P在BC之间时S=(2t 5)×=t
(4)存在,∵∠ADM+∠BAD=90 ,∠BCD=∠BAD,∴∠ADM+∠BCD=90 ,
∵∠MPB+∠BCD=90 ,∴∠MPB=∠ADM,
∵四边形ABCD是菱形,∴∠DAM=∠BAM,
∵AM=AM,∴△ADM≌△ABM,∴∠ADM=∠ABM,∴∠MPB=∠ABM,
∵MH⊥AB,∴PH=BH=2,∴BP=2BH=4,
∵AB=5,∴AP=1,∴t==
1 / 1
同课章节目录
- 第一章 二次根式
- 1.1 二次根式
- 1.2 二次根式的性质
- 1.3 二次根式的运算
- 第二章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程的应用
- 2.4 一元二次方程根与系数的关系(选学)
- 第三章 数据分析初步
- 3.1 平均数
- 3.2 中位数和众数
- 3.3 方差和标准差
- 第四章 平行四边形
- 4.1 多边形
- 4.2 平行四边形
- 4.3 中心对称
- 4.4 平行四边形的判定
- 4.5 三角形的中位线
- 4.6 反证法
- 第五章 特殊平行四边形
- 5.1 矩形
- 5.2 菱形
- 5.3 正方形
- 第六章 反比例函数
- 6.1 反比例函数
- 6.2 反比例函数的图象和性质
- 6.3 反比例函数的应用
