5.1.1 矩形的性质同步练习（含答案）

中小学教育资源及组卷应用平台
5.1　第1课时　矩形的性质
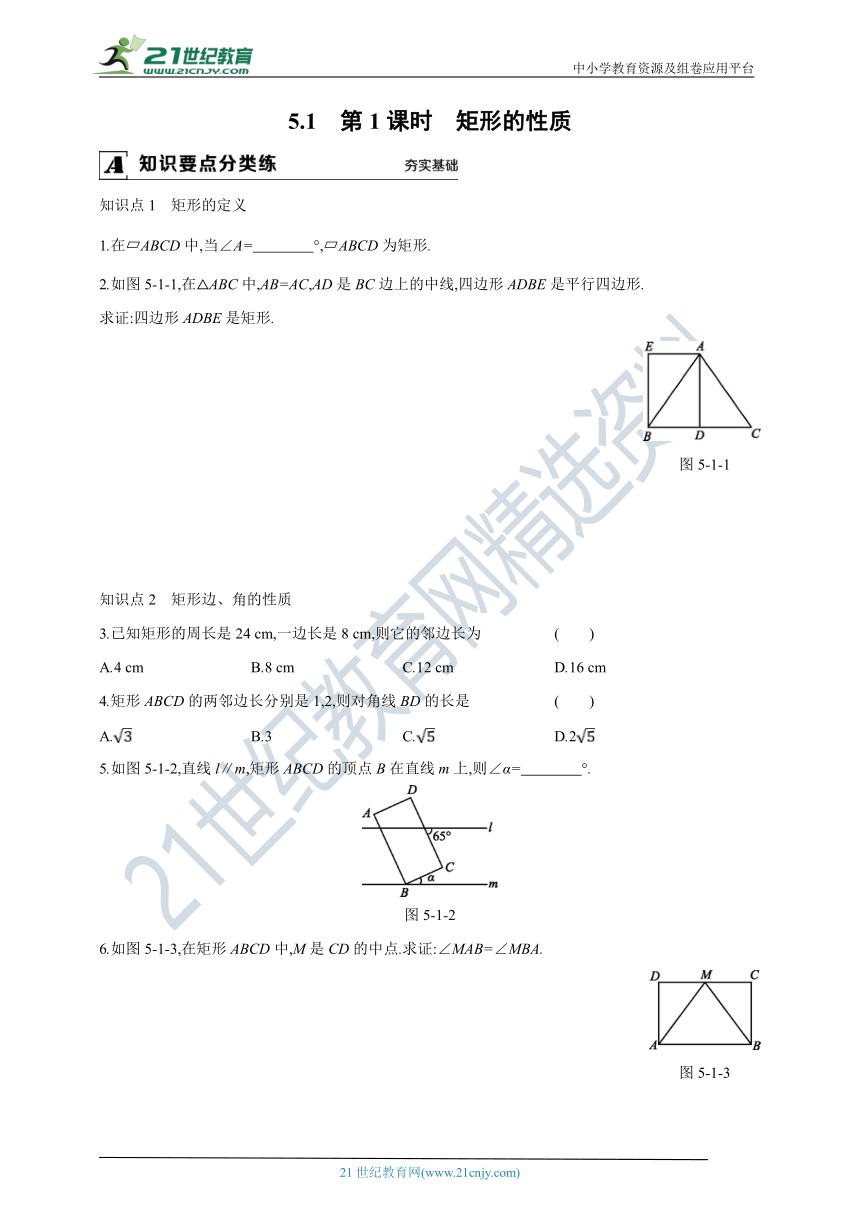
知识点1　矩形的定义
1.在 ABCD中,当∠A=　　　　°, ABCD为矩形.
2.如图5-1-1,在△ABC中,AB=AC,AD是BC边上的中线,四边形ADBE是平行四边形.
求证:四边形ADBE是矩形.
图5-1-1
知识点2　矩形边、角的性质
3.已知矩形的周长是24 cm,一边长是8 cm,则它的邻边长为 (　　)
A.4 cm B.8 cm C.12 cm D.16 cm
4.矩形ABCD的两邻边长分别是1,2,则对角线BD的长是 (　　)
A. B.3 C. D.2
5.如图5-1-2,直线l∥m,矩形ABCD的顶点B在直线m上,则∠α=　　　　°.
图5-1-2
6.如图5-1-3,在矩形ABCD中,M是CD的中点.求证:∠MAB=∠MBA.
图5-1-3
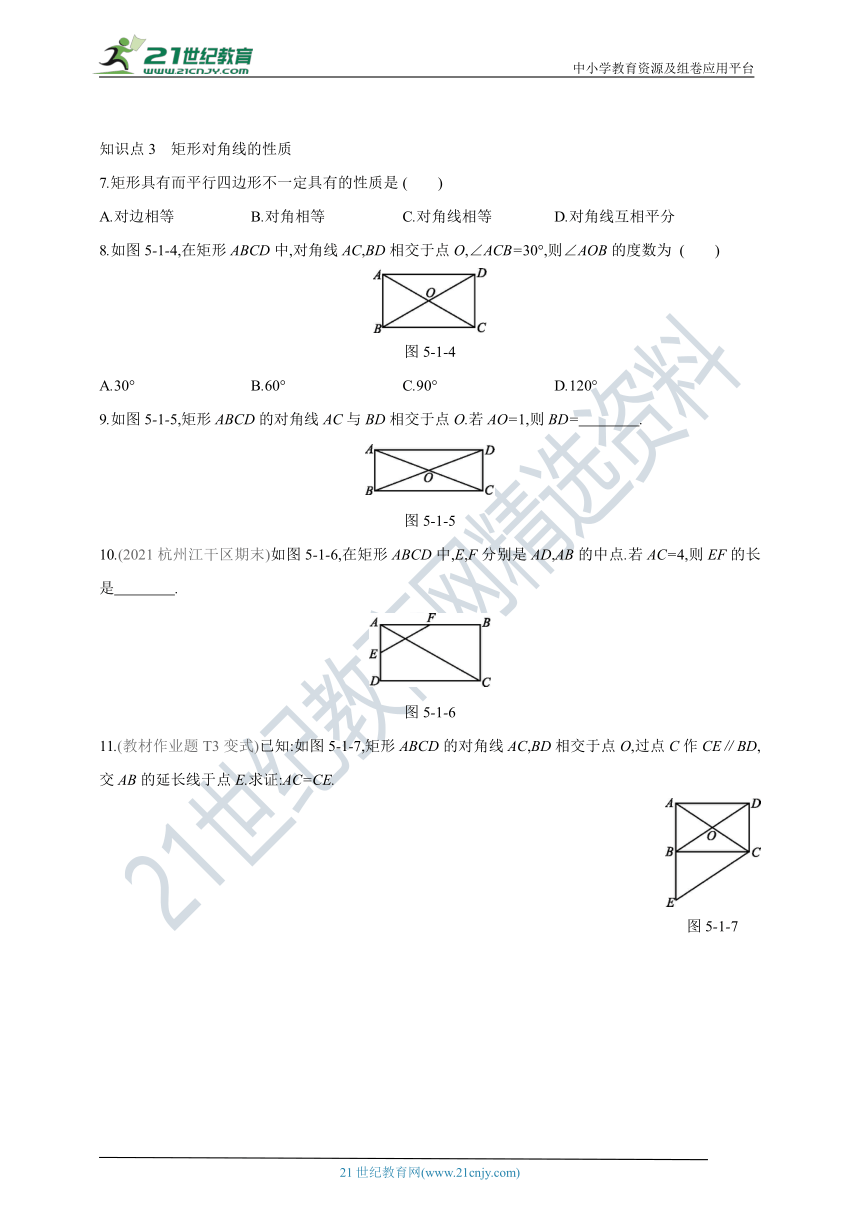
知识点3　矩形对角线的性质
7.矩形具有而平行四边形不一定具有的性质是 (　　)
A.对边相等 B.对角相等 C.对角线相等 D.对角线互相平分
8.如图5-1-4,在矩形ABCD中,对角线AC,BD相交于点O,∠ACB=30°,则∠AOB的度数为 (　　)
图5-1-4
A.30° B.60° C.90° D.120°
9.如图5-1-5,矩形ABCD的对角线AC与BD相交于点O.若AO=1,则BD=　　　　.
图5-1-5
10.(2021杭州江干区期末)如图5-1-6,在矩形ABCD中,E,F分别是AD,AB的中点.若AC=4,则EF的长是　　　　.
图5-1-6
11.(教材作业题T3变式)已知:如图5-1-7,矩形ABCD的对角线AC,BD相交于点O,过点C作CE∥BD,交AB的延长线于点E.求证:AC=CE.
图5-1-7
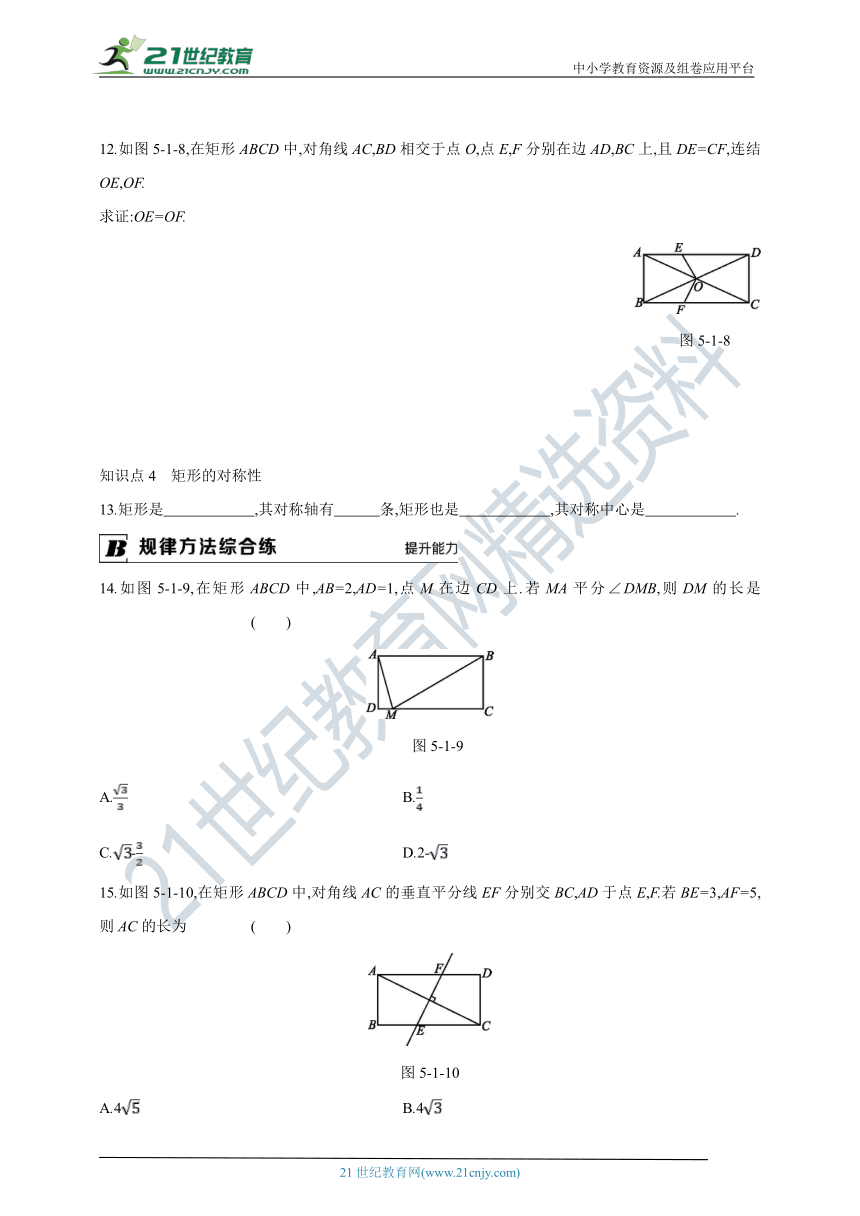
12.如图5-1-8,在矩形ABCD中,对角线AC,BD相交于点O,点E,F分别在边AD,BC上,且DE=CF,连结OE,OF.
求证:OE=OF.
图5-1-8
知识点4　矩形的对称性
13.矩形是　　　　　　,其对称轴有　　　条,矩形也是　　　　　　,其对称中心是　　　　　　.
14.如图5-1-9,在矩形ABCD中,AB=2,AD=1,点M在边CD上.若MA平分∠DMB,则DM的长是 (　　)
　图5-1-9
A. B.
C.- D.2-
15.如图5-1-10,在矩形ABCD中,对角线AC的垂直平分线EF分别交BC,AD于点E,F.若BE=3,AF=5,则AC的长为 (　　)
图5-1-10
A.4 B.4
C.10 D.8
16.如图5-1-11,四边形ABCD和四边形AEFC都是矩形,点B在EF边上.若矩形ABCD和矩形AEFC的面积分别是S1,S2,则S1,S2的大小关系是 (　　)
图5-1-11
A.S1>S2 B.S1=S2
C.S117.如图5-1-12所示,在矩形ABCD的对称轴l上找点P,使得△PAB,△PBC,△PDC,△PAD均为等腰三角形,则满足条件的点P有 (　　)
图5-1-12
A.5个 B.4个 C.3个 D.1个
18.(2021宁波)如图5-1-13是一个由5张纸片拼成的平行四边形ABCD,相邻纸片之间互不重叠也无缝隙,其中两张等腰直角三角形纸片的面积都为S1,另两张直角三角形纸片的面积都为S2,中间一张矩形纸片EFGH的面积为S3,FH与GE相交于点O.当△AEO,△BFO,△CGO,△DHO的面积相等时,下列结论一定成立的是 (　　)
图5-1-13
A.S1=S2 B.S1=S3 C.AB=AD D.EH=GH
详解详析
1.90
2.证明:∵AB=AC,AD是BC边上的中线,
∴AD⊥BC,∴∠ADB=90°.
又∵四边形ADBE是平行四边形,
∴四边形ADBE是矩形.
3.A
4.C　[解析] 因为矩形的每个角都是直角,所以两邻边和对角线构成直角三角形,所以BD==.
5.25
6.证明:∵四边形ABCD是矩形,M是CD的中点,
∴DM=CM,AD=BC,∠D=∠C=90°,
∴△ADM≌△BCM,
∴MA=MB,
∴∠MAB=∠MBA.
7.C
8.B
9.2　[解析] 在矩形ABCD中,∵对角线AC与BD相交于点O,AO=1,∴AO=CO=BO=DO=1,∴BD=2.故答案为2.
10.2　[解析] 如图,连结BD.
∵四边形ABCD是矩形,
∴BD=AC=4.
∵E,F分别是AD,AB的中点,
∴EF=BD=2.
故答案为2.
11.证明:在矩形ABCD中,AC=BD,CD∥AB.
又∵CE∥BD,
∴四边形BECD是平行四边形,
∴BD=CE,∴AC=CE.
12.证明:∵四边形ABCD为矩形,
∴∠ADC=∠BCD=90°,AC=BD,OD=BD,OC=AC,
∴OD=OC,
∴∠ODC=∠OCD,
∴∠ADC-∠ODC=∠BCD-∠OCD,
即∠EDO=∠FCO.
又∵DE=CF,OD=OC,
∴△ODE≌△OCF,∴OE=OF.
13.轴对称图形　2　中心对称图形　对角线的交点
14.D　[解析] ∵四边形ABCD是矩形,
∴CD=AB=2,AB∥CD,BC=AD=1,∠C=90°,
∴∠BAM=∠AMD.
∵MA平分∠DMB,∴∠AMD=∠AMB,
∴∠BAM=∠AMB,∴BM=AB=2,
则CM===,
∴DM=CD-CM=2-.
故选D.
15.A　[解析] 如图,连结AE,设EF与AC的交点为O.
∵EF是AC的垂直平分线,
∴OA=OC,AE=CE.
∵四边形ABCD是矩形,
∴∠B=90°,AD∥BC,
∴∠OAF=∠OCE.
在△AOF和△COE中,∵
∴△AOF≌△COE(ASA),
∴AF=CE=5,
则AE=CE=5,BC=BE+CE=3+5=8,
∴AB===4,
∴AC===4.
故选A.
16.B　[解析] 矩形ABCD的面积S1=2S△ABC,而S△ABC=S矩形AEFC=S2,所以S1=S2.
故选B.
17.A　[解析] 如图①,作AB或DC的垂直平分线交l于点P1,则点P1符合题意;
如图②,在l上作点P2,使P2A=AB,同理,在l上作点P3,使P3C=DC,则点P2,P3均符合题意;
如图③,在l上作点P4,使BP4=AB,同理,在l上作点P5,使P5D=DC,则点P4,P5均符合题意.
综上所述,符合条件的点P有5个.
故选A.
18.A　[解析] 如图,连结DG,AH,过点O作OJ⊥DE于点J.
∵四边形EFGH是矩形,
∴OH=OF,EF=GH,∠HEF=90°.
∵OJ⊥DE,
∴∠OJH=∠HEF=90°,
∴OJ∥EF.
∵HO=OF,
∴HJ=JE,
∴EF=GH=2OJ.
∵S△DHO=DH·OJ,S△DGH=DH·GH,
∴S△DGH=2S△DHO,
同法可证S△AEH=2S△AEO.
∵S△DHO=S△AEO,
∴S△DGH=S△AEH.
∵S△DGC=CG·DH,S△ADH=DH·AE,CG=AE,
∴S△DGC=S△ADH,
∴S△DHC=S△ADE,
∴S1=S2.
故选A.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 （共 2 页）
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)