5.3.2 正方形的性质同步练习(含答案)
文档属性
| 名称 | 5.3.2 正方形的性质同步练习(含答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-04-25 20:11:01 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
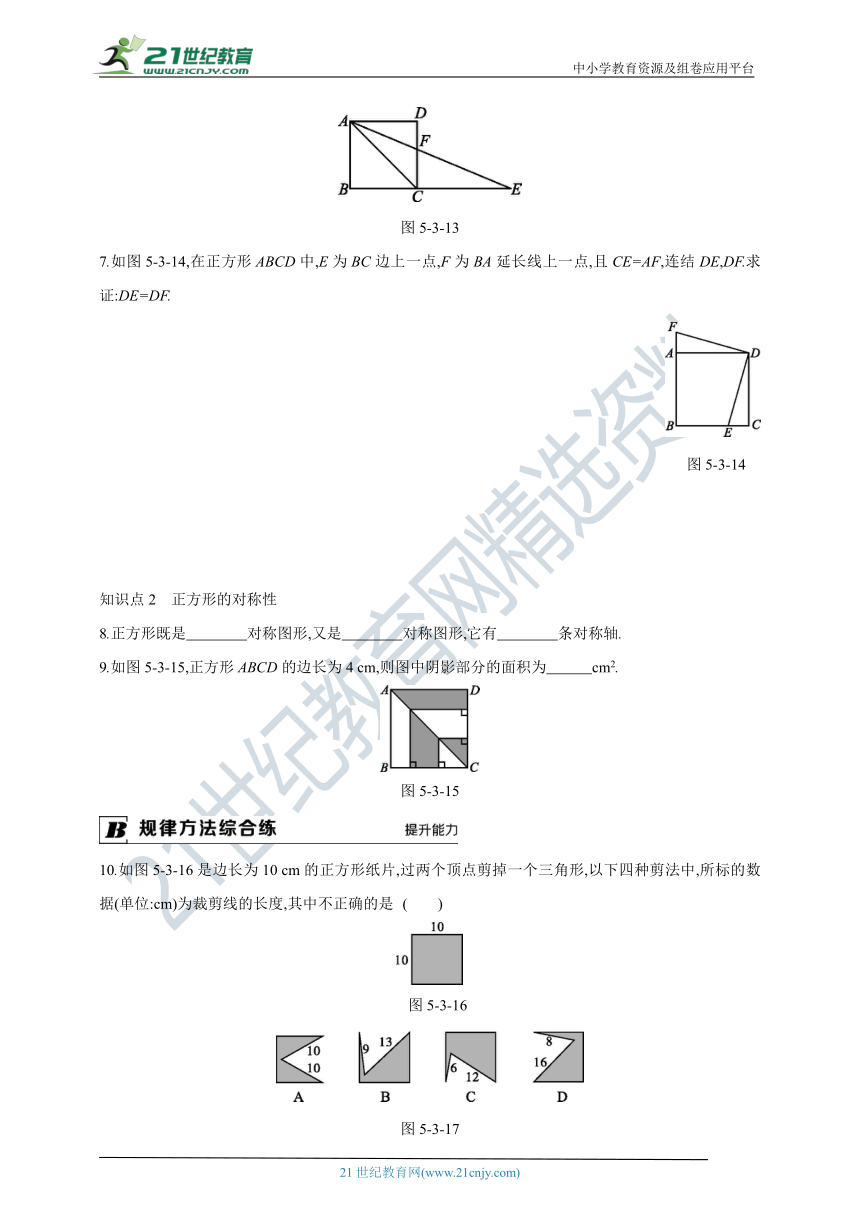
5.3 第2课时 正方形的性质
知识点1 正方形的性质
1.(2021杭州滨江区期末)正方形具有而矩形不一定具有的性质是 ( )
A.对角互补 B.对角线相等
C.四个角相等 D.对角线互相垂直
2.如图5-3-10,已知正方形ABCD的两条对角线相交于点O,那么此图中等腰直角三角形有 ( )
图5-3-10
A.4个 B.6个 C.8个 D.10个
3.若正方形的一条对角线的长为4,则这个正方形的面积是 ( )
A.8 B.4 C.8 D.16
4.如图5-3-11,将正方形纸片ABCD折叠,使边AB,CB均落在对角线BD上,得折痕BE,BF,则∠EBF的大小为 ( )
图5-3-11
A.15° B.30° C.45° D.60°
5.如图5-3-12,已知正方形ABCD,点E在边DC上,DE=3,EC=1,则AE的长为 .
图5-3-12
6.(教材课内练习T2变式)如图5-3-13,在正方形ABCD的边BC的延长线上取一点E,使CE=AC,连结AE交CD于点F,则∠AFD= °.
图5-3-13
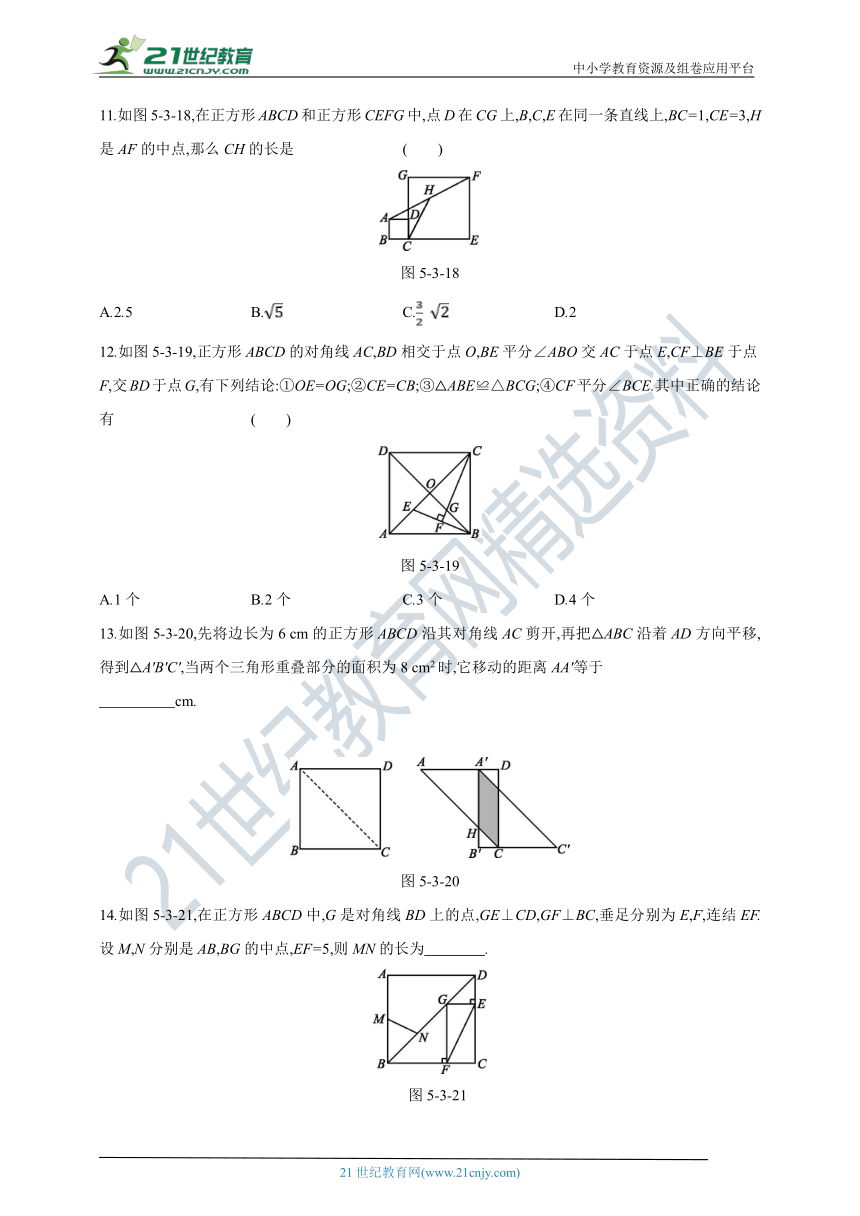
7.如图5-3-14,在正方形ABCD中,E为BC边上一点,F为BA延长线上一点,且CE=AF,连结DE,DF.求证:DE=DF.
图5-3-14
知识点2 正方形的对称性
8.正方形既是 对称图形,又是 对称图形,它有 条对称轴.
9.如图5-3-15,正方形ABCD的边长为4 cm,则图中阴影部分的面积为 cm2.
图5-3-15
10.如图5-3-16是边长为10 cm的正方形纸片,过两个顶点剪掉一个三角形,以下四种剪法中,所标的数据(单位:cm)为裁剪线的长度,其中不正确的是 ( )
图5-3-16
图5-3-17
11.如图5-3-18,在正方形ABCD和正方形CEFG中,点D在CG上,B,C,E在同一条直线上,BC=1,CE=3,H是AF的中点,那么CH的长是 ( )
图5-3-18
A.2.5 B. C. D.2
12.如图5-3-19,正方形ABCD的对角线AC,BD相交于点O,BE平分∠ABO交AC于点E,CF⊥BE于点F,交BD于点G,有下列结论:①OE=OG;②CE=CB;③△ABE≌△BCG;④CF平分∠BCE.其中正确的结论有 ( )
图5-3-19
A.1个 B.2个 C.3个 D.4个
13.如图5-3-20,先将边长为6 cm的正方形ABCD沿其对角线AC剪开,再把△ABC沿着AD方向平移,得到△A'B'C',当两个三角形重叠部分的面积为8 cm2时,它移动的距离AA'等于
cm.
图5-3-20
14.如图5-3-21,在正方形ABCD中,G是对角线BD上的点,GE⊥CD,GF⊥BC,垂足分别为E,F,连结EF.设M,N分别是AB,BG的中点,EF=5,则MN的长为 .
图5-3-21
15.如图5-3-22,在正方形ABCD中,E,F分别为AB,AD上的点,且AE=AF,M是EF的中点,连结CM,CE.
(1)求证:CM⊥EF;
(2)设正方形ABCD的边长为2,若五边形BCDFE的面积为,请直接写出CM的长.
图5-3-22
16.如图5-3-23,已知正方形ABCD和正方形CEFG的边长分别为10 cm和5 cm,点B,C,E在同一条直线上,点G在CD上.
(1)△BFD的面积为 cm2.
(2)若将正方形CEFG的边长改为8 cm,则△BFD的面积为多少
(3)若去掉“正方形CEFG的边长为5 cm”这个条件,你还能求出△BFD的面积吗 若能,请直接写出;若不能,请说明理由.
图5-3-23
详解详析
1.D
2.C [解析] ∵四边形ABCD是正方形,∴AB=BC=CD=AD,∠ABC=∠BCD=∠CDA=∠BAD=90°,OA=OB=OC=OD,AC⊥BD,∴△ABC,△ADC,△ABD,△BCD,△AOB,△BOC,△AOD,△COD都是等腰直角三角形.故选C.
3.A [解析] ∵正方形的一条对角线长为4,
∴这个正方形的面积=×4×4=8.
故选A.
4.C
5.5 [解析] ∵四边形ABCD是正方形,
∴AD=DC,∠D=90°.
∵DE=3,EC=1,∴AD=DC=4.
在Rt△ADE中,由勾股定理,
得AE===5.
6.67.5
7.证明:在正方形ABCD中,AD=CD,∠DAB=∠C=90°,
∴∠DAF=90°=∠C.
在△DCE和△DAF中,∵
∴△DCE≌△DAF,∴DE=DF.
8.中心 轴 4
9.8
10.D [解析] 选项D不正确.理由:∵正方形的边长为10,∴对角线长=10≈14.
∵16>14,
∴这个图形不可能存在.故选D.
11.B 12.D
13.2或4 [解析] 由题意,易得阴影部分为平行四边形.
令AA'=x.
由图可知A'D=6-x,A'H=x,
∴S阴影=A'H·A'D=x(6-x)=8,
解得x=2或x=4,∴AA'=2或4.
14.2.5
15.解:(1)证明:如图,连结CF.
∵四边形ABCD是正方形,
∴AB=AD=BC=CD,∠B=∠D=90°.
又∵AE=AF,∴BE=DF,
∴△BCE≌△DCF(SAS),∴CE=CF.
又∵M是EF的中点,∴CM⊥EF.
(2)连结AM,如图.
∵四边形ABCD是正方形,
∴∠EAF=90°.
又∵AE=AF,
∴△AEF是等腰直角三角形.
∵M是EF的中点,
∴AM⊥EF,EF=2AM,∴∠AME=90°.
由(1)知CM⊥EF,∴∠CME=90°,
∴∠AME+∠CME=180°,
即A,M,C三点共线.
∵正方形ABCD的边长为2,
∴正方形ABCD的面积=4.
∵五边形BCDFE的面积为,
∴△AEF的面积=,
∴AM·EF=AM·2AM=,
∴AM=.
易得AC=2,∴CM=.
16.解:(1)50
(2)延长EF,AD交于点M,则四边形ABEM为矩形.
S△BFD=S矩形ABEM-S△BEF-S△MDF-S△ABD=(10+8)×10-×(10+8)×8-×(10-8)×8-×10×10=50(cm2).
(3)能.△BFD的面积为50 cm2.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
5.3 第2课时 正方形的性质
知识点1 正方形的性质
1.(2021杭州滨江区期末)正方形具有而矩形不一定具有的性质是 ( )
A.对角互补 B.对角线相等
C.四个角相等 D.对角线互相垂直
2.如图5-3-10,已知正方形ABCD的两条对角线相交于点O,那么此图中等腰直角三角形有 ( )
图5-3-10
A.4个 B.6个 C.8个 D.10个
3.若正方形的一条对角线的长为4,则这个正方形的面积是 ( )
A.8 B.4 C.8 D.16
4.如图5-3-11,将正方形纸片ABCD折叠,使边AB,CB均落在对角线BD上,得折痕BE,BF,则∠EBF的大小为 ( )
图5-3-11
A.15° B.30° C.45° D.60°
5.如图5-3-12,已知正方形ABCD,点E在边DC上,DE=3,EC=1,则AE的长为 .
图5-3-12
6.(教材课内练习T2变式)如图5-3-13,在正方形ABCD的边BC的延长线上取一点E,使CE=AC,连结AE交CD于点F,则∠AFD= °.
图5-3-13
7.如图5-3-14,在正方形ABCD中,E为BC边上一点,F为BA延长线上一点,且CE=AF,连结DE,DF.求证:DE=DF.
图5-3-14
知识点2 正方形的对称性
8.正方形既是 对称图形,又是 对称图形,它有 条对称轴.
9.如图5-3-15,正方形ABCD的边长为4 cm,则图中阴影部分的面积为 cm2.
图5-3-15
10.如图5-3-16是边长为10 cm的正方形纸片,过两个顶点剪掉一个三角形,以下四种剪法中,所标的数据(单位:cm)为裁剪线的长度,其中不正确的是 ( )
图5-3-16
图5-3-17
11.如图5-3-18,在正方形ABCD和正方形CEFG中,点D在CG上,B,C,E在同一条直线上,BC=1,CE=3,H是AF的中点,那么CH的长是 ( )
图5-3-18
A.2.5 B. C. D.2
12.如图5-3-19,正方形ABCD的对角线AC,BD相交于点O,BE平分∠ABO交AC于点E,CF⊥BE于点F,交BD于点G,有下列结论:①OE=OG;②CE=CB;③△ABE≌△BCG;④CF平分∠BCE.其中正确的结论有 ( )
图5-3-19
A.1个 B.2个 C.3个 D.4个
13.如图5-3-20,先将边长为6 cm的正方形ABCD沿其对角线AC剪开,再把△ABC沿着AD方向平移,得到△A'B'C',当两个三角形重叠部分的面积为8 cm2时,它移动的距离AA'等于
cm.
图5-3-20
14.如图5-3-21,在正方形ABCD中,G是对角线BD上的点,GE⊥CD,GF⊥BC,垂足分别为E,F,连结EF.设M,N分别是AB,BG的中点,EF=5,则MN的长为 .
图5-3-21
15.如图5-3-22,在正方形ABCD中,E,F分别为AB,AD上的点,且AE=AF,M是EF的中点,连结CM,CE.
(1)求证:CM⊥EF;
(2)设正方形ABCD的边长为2,若五边形BCDFE的面积为,请直接写出CM的长.
图5-3-22
16.如图5-3-23,已知正方形ABCD和正方形CEFG的边长分别为10 cm和5 cm,点B,C,E在同一条直线上,点G在CD上.
(1)△BFD的面积为 cm2.
(2)若将正方形CEFG的边长改为8 cm,则△BFD的面积为多少
(3)若去掉“正方形CEFG的边长为5 cm”这个条件,你还能求出△BFD的面积吗 若能,请直接写出;若不能,请说明理由.
图5-3-23
详解详析
1.D
2.C [解析] ∵四边形ABCD是正方形,∴AB=BC=CD=AD,∠ABC=∠BCD=∠CDA=∠BAD=90°,OA=OB=OC=OD,AC⊥BD,∴△ABC,△ADC,△ABD,△BCD,△AOB,△BOC,△AOD,△COD都是等腰直角三角形.故选C.
3.A [解析] ∵正方形的一条对角线长为4,
∴这个正方形的面积=×4×4=8.
故选A.
4.C
5.5 [解析] ∵四边形ABCD是正方形,
∴AD=DC,∠D=90°.
∵DE=3,EC=1,∴AD=DC=4.
在Rt△ADE中,由勾股定理,
得AE===5.
6.67.5
7.证明:在正方形ABCD中,AD=CD,∠DAB=∠C=90°,
∴∠DAF=90°=∠C.
在△DCE和△DAF中,∵
∴△DCE≌△DAF,∴DE=DF.
8.中心 轴 4
9.8
10.D [解析] 选项D不正确.理由:∵正方形的边长为10,∴对角线长=10≈14.
∵16>14,
∴这个图形不可能存在.故选D.
11.B 12.D
13.2或4 [解析] 由题意,易得阴影部分为平行四边形.
令AA'=x.
由图可知A'D=6-x,A'H=x,
∴S阴影=A'H·A'D=x(6-x)=8,
解得x=2或x=4,∴AA'=2或4.
14.2.5
15.解:(1)证明:如图,连结CF.
∵四边形ABCD是正方形,
∴AB=AD=BC=CD,∠B=∠D=90°.
又∵AE=AF,∴BE=DF,
∴△BCE≌△DCF(SAS),∴CE=CF.
又∵M是EF的中点,∴CM⊥EF.
(2)连结AM,如图.
∵四边形ABCD是正方形,
∴∠EAF=90°.
又∵AE=AF,
∴△AEF是等腰直角三角形.
∵M是EF的中点,
∴AM⊥EF,EF=2AM,∴∠AME=90°.
由(1)知CM⊥EF,∴∠CME=90°,
∴∠AME+∠CME=180°,
即A,M,C三点共线.
∵正方形ABCD的边长为2,
∴正方形ABCD的面积=4.
∵五边形BCDFE的面积为,
∴△AEF的面积=,
∴AM·EF=AM·2AM=,
∴AM=.
易得AC=2,∴CM=.
16.解:(1)50
(2)延长EF,AD交于点M,则四边形ABEM为矩形.
S△BFD=S矩形ABEM-S△BEF-S△MDF-S△ABD=(10+8)×10-×(10+8)×8-×(10-8)×8-×10×10=50(cm2).
(3)能.△BFD的面积为50 cm2.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
- 第一章 二次根式
- 1.1 二次根式
- 1.2 二次根式的性质
- 1.3 二次根式的运算
- 第二章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程的应用
- 2.4 一元二次方程根与系数的关系(选学)
- 第三章 数据分析初步
- 3.1 平均数
- 3.2 中位数和众数
- 3.3 方差和标准差
- 第四章 平行四边形
- 4.1 多边形
- 4.2 平行四边形
- 4.3 中心对称
- 4.4 平行四边形的判定
- 4.5 三角形的中位线
- 4.6 反证法
- 第五章 特殊平行四边形
- 5.1 矩形
- 5.2 菱形
- 5.3 正方形
- 第六章 反比例函数
- 6.1 反比例函数
- 6.2 反比例函数的图象和性质
- 6.3 反比例函数的应用
