2021-2022学年浙教版数学8年级下学期 第4章 平行四边形 综合测评(含答案)
文档属性
| 名称 | 2021-2022学年浙教版数学8年级下学期 第4章 平行四边形 综合测评(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-01 12:54:57 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
2021-2022学年浙教版数学8年级下学期
第4章 平行四边形 综合测评
一、单选题(共10题;共30分)
1.(3分)若用反证法证明命题“四边形中至少有一个角是钝角或直角”时,则首先应该假设这个四边形中( )
A.至少有一个角是钝角或直角 B.没有一个角是锐角
C.没有一个角是钝角或直角 D.每一个角都是钝角或直角
2.(3分)在四边形ABCD中,∠A,∠B,∠C,∠D度数之比为1:2:3:3,则∠B的度数为( )
A.30° B.40° C.80° D.120°
3.(3分)在四边形ABCD中,O是对角线交点,下列条件中,不能判定四边形ABCD是平行四边形的是( ).
A.AD//BC,AD=BC B.AB=DC,AD=BC
C.AB//DC,AD=BC D.OA=OC,OD=OB
4.(3分)如图,在 中,CE平分∠BCD,交AB于点E,EA=3,EB=5,ED=4.则CE的长是( )
A.5 B.6 C.4 D.5
5.(3分)如图,在△ABC中,D,E分别是AB,BC的中点,点F在DE延长线上,添加一个条件使四边形ADFC为平行四边形,则这个条件是( )
A. B. C. D.
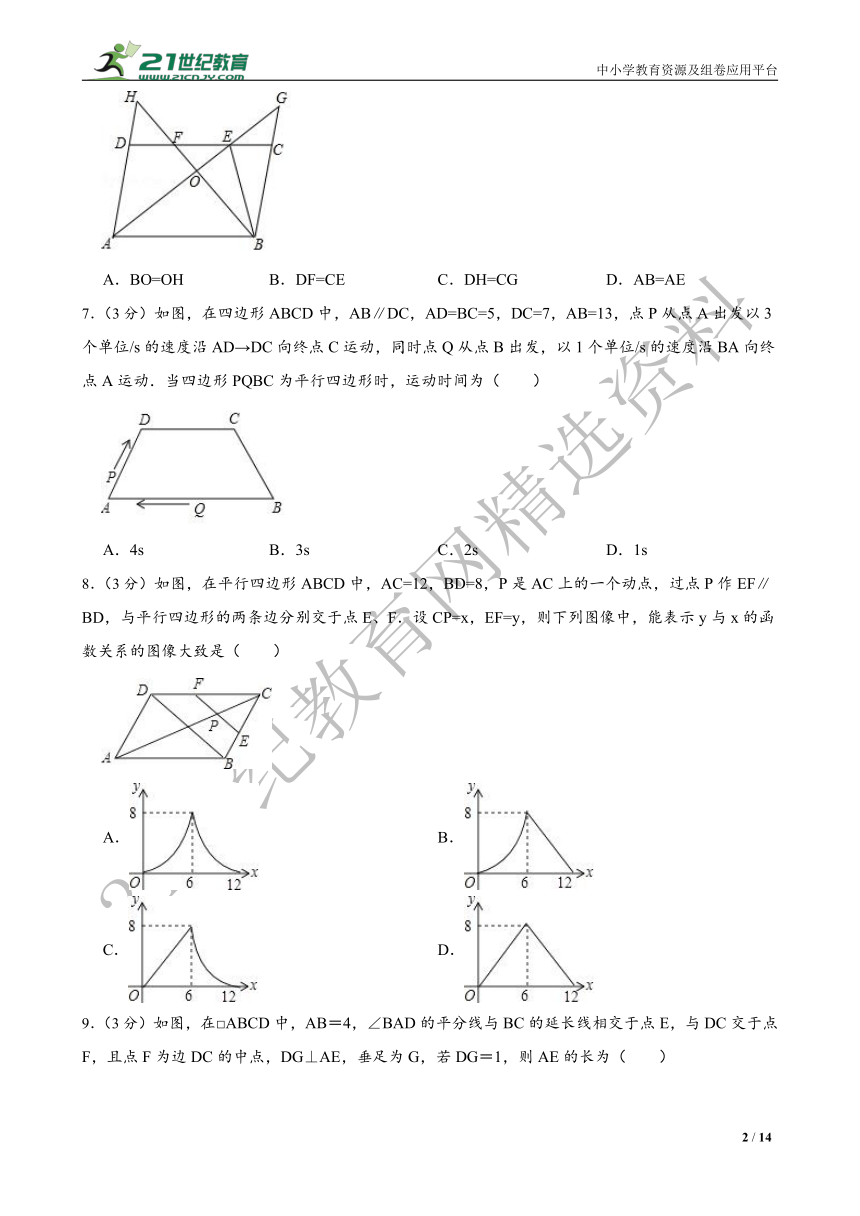
6.(3分)如图,在 ABCD中,∠DAB的平分线交CD于点E,交BC的延长线于点G,∠ABC的平分线交CD于点F,交AD的延长线于点H,AG与BH交于点O,连接BE,下列结论错误的是( )
A.BO=OH B.DF=CE C.DH=CG D.AB=AE
7.(3分)如图,在四边形ABCD中,AB∥DC,AD=BC=5,DC=7,AB=13,点P从点A出发以3个单位/s的速度沿AD→DC向终点C运动,同时点Q从点B出发,以1个单位/s的速度沿BA向终点A运动.当四边形PQBC为平行四边形时,运动时间为( )
A.4s B.3s C.2s D.1s
8.(3分)如图,在平行四边形ABCD中,AC=12,BD=8,P是AC上的一个动点,过点P作EF∥BD,与平行四边形的两条边分别交于点E、F.设CP=x,EF=y,则下列图像中,能表示y与x的函数关系的图像大致是( )
A. B.
C. D.
9.(3分)如图,在□ABCD中,AB=4,∠BAD的平分线与BC的延长线相交于点E,与DC交于点F,且点F为边DC的中点,DG⊥AE,垂足为G,若DG=1,则AE的长为( )
A.2 B.4 C.4 D.8
10.(3分)如图,已知△ABC是边长为3的等边三角形,点D是边BC上的一点,且BD=1,以AD为边作等边△ADE,过点E作EF∥BC,交AC于点F,连接BF,则下列结论中①△ABD≌△BCF;②四边形BDEF是平行四边形;③S四边形BDEF= ;④S△AEF= .其中正确的有( )
A.1个 B.2个 C.3个 D.4个
二、填空题(共6题;共24分)
11.(4分)如图,平移图形M,与图形N可以拼成一个平行四边形,则图中α的度数是 °.
12.(4分)将正三角形、正四边形、正五边形按如图所示的位置摆放.如果∠3=30°,那么∠1+∠2= °
13.(4分)如图,已知平行四边形ABCD中,∠BCD的平分线交边AD于E,∠ABC的平分线交AD于F,CD=10,AE=4,则EF= .
14.(4分)如图,在□ABCD中,连结BD,且BD=CD,过点A作AM⊥BD于点M,过点D作DN⊥AB于点N,且DN=5 ,在DB的延长线上取一点P,满足∠ABD=∠MAP+∠PAB,则AP= 。
15.(4分)如图,在四边形ABCD中,∠A+∠B=200°,作∠ADC、∠BCD的平分线交于点O1称为第1次操作,作∠O1DC、∠O1CD的平分线交于点O2称为第2次操作,作∠O2DC、∠O2CD的平分线交于点O3称为第3次操作,…,则第5次操作后∠CO5D的度数是 .
16.(4分)如图,在图(1)中,A1、B1、C1分别是△ABC的边BC、CA、AB的中点,在图(2)中,A2、B2、C2分别是△A1B1C1的边B1C1、C1A1、A1B1的中点,…,按此规律,则第n个图形中平行四边形的个数共有 个
三、综合题(共7题;共66分)
17.(6分)如图,点B、E、C、F在一条直线上,AB=DF,AC=DE,BE=FC.
(1)(3分)求证:△ABC≌△DFE;
(2)(3分)连接AF、BD,求证:四边形ABDF是平行四边形.
18.(8分)已知:平行四边形ABCD中,对角线AC、BD相交于点O.BD=2AD,E、F、G分别是OC、OD、AB的中点.
求证:
(1)(4分)BE⊥AC;
(2)(4分)EG=EF.
19.(8分)如图,已知,在 中,点D是边AC的中点,点E是边BC的延长线上一点,过点A作BE的平行线与线段ED的延长线相交于点F,连结AE.
(1)(4分)求证:AF=CE.
(2)(4分)连结CF,交边AB于点G,如果CF⊥AB,求证: .
20.(10分)如图,在平行四边形 中, 是 的中点,延长 到点 ,使 ,连结 ,
(1)(5分)求证:四边形 是平行四边形;
(2)(5分)若 , , ,求 的长.
21.(10分)如图,一块平行四边形场地ABCD,测得∠ABC=60°,AB=2,AD=4,AE⊥BD于点E,CF⊥BD于点F,连接CE,AF.现计划在四边形AECF区域内种植花草;
(1)(5分)求证:四边形AECF是平行四边形;
(2)(5分)求四边形AECF的面积.
22.(10分)如图,平行四边形ABCD中,点O是对角线AC的中点,点M为BC上一点,连接AM,且AB=AM,点E为BM中点,AF⊥AB,连接EF,延长FO交AB于点N.
(1)(5分)若BM=4,MC=3,AC= ,求AM的长度;
(2)(5分)若∠ACB=45°,求证:AN+AF= EF.
23.(14分)如图,在四边形ABCD中,AD∥BC,AD=12cm,BC=15cm,点P自点A向D以1cm/s的速度运动,到D点即停止.点Q自点C向B以2cm/s的速度运动,到B点即停止,点P,Q同时出发,设运动时间为t(s).
(1)(1分)用含t的代数式表示:
AP= ;DP= ;BQ= ;CQ= .
(2)(5分)当t为何值时,四边形APQB是平行四边形?
(3)(5分)当t为何值时,四边形PDCQ是平行四边形?
答案解析部分
1.【答案】C
2.【答案】C
3.【答案】C
4.【答案】C
5.【答案】B
6.【答案】D
7.【答案】B
8.【答案】D
9.【答案】B
10.【答案】C
11.【答案】30
12.【答案】72
13.【答案】6
14.【答案】10
15.【答案】175°
16.【答案】3n
17.【答案】(1)证明:∵BE=FC,
∴BC=EF,
在△ABC和△DFE中,
,
∴△ABC≌△DFE(SSS)
(2)解:由(1)知△ABC≌△DFE,
∴∠ABC=∠DFE,
∴AB∥DF,
∵AB=DF,
∴四边形ABDF是平行四边形.
18.【答案】(1)证明:∵四边形ABCD是平行四边形,
∴AD=BC,BD=2BO.
∵BD=2AD,
∴BO=BC,
又∵点E是OC中点,
∴BE⊥AC;
(2)证明:由(1)知BE⊥AC
又∵点G是AB中点,
∴EG是Rt△ABE斜边上的中线,
∴EG=AB,
又∵EF是△OCD的中位线,
∴EF=CD,
又∵AB=CD,
∴EG=EF.
19.【答案】(1)证明: 点D是边AC的中点,
,
,
,
在 和 中, ,
,
;
(2)解:由(1)知, ,
,
四边形AECF是平行四边形,
,
,
,
,
.
20.【答案】(1)证明: ∵DF=CE,且DF∥CE。 ∴四边形CEDF是平行四边形
(2)解:如图,过点D作DH⊥BE于点H,
∴在Rt△DHE中,根据勾股定理,得
21.【答案】(1)证明:∵四边形ABCD是平行四边形,
∴S△ABD=S△CBD,
∵AE⊥BD,CF⊥BD,
∴AE∥CF
∴AE BD= CF BD,
∴AE=CF,
∴四边形AECF是平行四边形
(2)解:过点B作BH⊥AD,交DA的延长线于点H,∵∠ABC=60°,
∴∠ABH=30°,
∵AB=2,
∴AH=1,BH= ,
∴DH=AH+AD=1+4=5,
∴BD= ,
∵S△ABD= BD AE= AD BH,
即 × ×AE= ×4× ,
解得:AE= ,
∴BE= ,
同理:DF=BE= ,
∴EF=BD﹣BE﹣DF= ,
∴S四边形AECF=EF AE=
22.【答案】(1)解:如图1中,连接AE.
∵AB=AM,BE=EM,
∴AE⊥BM,
在Rt△ACE中,∵AC= ,EC=EM+CM=5,
∴AE= = ,
在Rt△AEM中,AM= =
(2)解:如图,连接AE,作EH⊥AF于F,EG⊥DC交DC的延长线于E.
∵∠AEC=∠AFC=90°,
∴∠AEC+∠AFC=90°,
∴A,E,C,F四点共圆,
∴∠AFE=∠ACE=45°,
∴∠EFA=∠EFG=45°,
∵EH⊥FA,EG⊥FG,
∴EH=EG,
∵∠ACE=∠EAC=45°,
∴AE=EC,
∴Rt△EHA≌Rt△EGC(HL),
∴AH=CG,
∵EF=EF,EH=EG,
∴Rt△EHF≌Rt△EGF(HL),
∴FH=FG,
∵AB∥CD,
∴∠OAN=∠OCF,
∵∠AON=∠COF,OA=OC,
∴△AON≌△COF(ASA),
∴AN=CF,
∴AN+AF=FC+AF=FG﹣CG+FH+AH=2FH,
∵EF= FH,
∴AN+AF= EF
23.【答案】(1)t;12﹣t;15﹣2t;2t
(2)解:根据题意有AP=t,CQ=2t,PD=12﹣t,BQ=15﹣2t.
∵AD∥BC,∴当AP=BQ时,四边形APQB是平行四边形.
∴t=15﹣2t,解得t=5.
∴运动5s时四边形APQB是平行四边形
(3)解:由AP=tcm,CQ=2tcm,
∵AD=12cm,BC=15cm,
∴PD=AD﹣AP=12﹣t,
如图1当PQ∥CD,且PQ=CD时,
∵AD∥BC,即PD∥QC,
∴四边形PQCD为平行四边形,
∴PQ=CD,PD=CQ,
∴12﹣t=2t,
解得t=4s,
即当t=4s时,四边形PDCQ是平行四边形.
1 / 1
2021-2022学年浙教版数学8年级下学期
第4章 平行四边形 综合测评
一、单选题(共10题;共30分)
1.(3分)若用反证法证明命题“四边形中至少有一个角是钝角或直角”时,则首先应该假设这个四边形中( )
A.至少有一个角是钝角或直角 B.没有一个角是锐角
C.没有一个角是钝角或直角 D.每一个角都是钝角或直角
2.(3分)在四边形ABCD中,∠A,∠B,∠C,∠D度数之比为1:2:3:3,则∠B的度数为( )
A.30° B.40° C.80° D.120°
3.(3分)在四边形ABCD中,O是对角线交点,下列条件中,不能判定四边形ABCD是平行四边形的是( ).
A.AD//BC,AD=BC B.AB=DC,AD=BC
C.AB//DC,AD=BC D.OA=OC,OD=OB
4.(3分)如图,在 中,CE平分∠BCD,交AB于点E,EA=3,EB=5,ED=4.则CE的长是( )
A.5 B.6 C.4 D.5
5.(3分)如图,在△ABC中,D,E分别是AB,BC的中点,点F在DE延长线上,添加一个条件使四边形ADFC为平行四边形,则这个条件是( )
A. B. C. D.
6.(3分)如图,在 ABCD中,∠DAB的平分线交CD于点E,交BC的延长线于点G,∠ABC的平分线交CD于点F,交AD的延长线于点H,AG与BH交于点O,连接BE,下列结论错误的是( )
A.BO=OH B.DF=CE C.DH=CG D.AB=AE
7.(3分)如图,在四边形ABCD中,AB∥DC,AD=BC=5,DC=7,AB=13,点P从点A出发以3个单位/s的速度沿AD→DC向终点C运动,同时点Q从点B出发,以1个单位/s的速度沿BA向终点A运动.当四边形PQBC为平行四边形时,运动时间为( )
A.4s B.3s C.2s D.1s
8.(3分)如图,在平行四边形ABCD中,AC=12,BD=8,P是AC上的一个动点,过点P作EF∥BD,与平行四边形的两条边分别交于点E、F.设CP=x,EF=y,则下列图像中,能表示y与x的函数关系的图像大致是( )
A. B.
C. D.
9.(3分)如图,在□ABCD中,AB=4,∠BAD的平分线与BC的延长线相交于点E,与DC交于点F,且点F为边DC的中点,DG⊥AE,垂足为G,若DG=1,则AE的长为( )
A.2 B.4 C.4 D.8
10.(3分)如图,已知△ABC是边长为3的等边三角形,点D是边BC上的一点,且BD=1,以AD为边作等边△ADE,过点E作EF∥BC,交AC于点F,连接BF,则下列结论中①△ABD≌△BCF;②四边形BDEF是平行四边形;③S四边形BDEF= ;④S△AEF= .其中正确的有( )
A.1个 B.2个 C.3个 D.4个
二、填空题(共6题;共24分)
11.(4分)如图,平移图形M,与图形N可以拼成一个平行四边形,则图中α的度数是 °.
12.(4分)将正三角形、正四边形、正五边形按如图所示的位置摆放.如果∠3=30°,那么∠1+∠2= °
13.(4分)如图,已知平行四边形ABCD中,∠BCD的平分线交边AD于E,∠ABC的平分线交AD于F,CD=10,AE=4,则EF= .
14.(4分)如图,在□ABCD中,连结BD,且BD=CD,过点A作AM⊥BD于点M,过点D作DN⊥AB于点N,且DN=5 ,在DB的延长线上取一点P,满足∠ABD=∠MAP+∠PAB,则AP= 。
15.(4分)如图,在四边形ABCD中,∠A+∠B=200°,作∠ADC、∠BCD的平分线交于点O1称为第1次操作,作∠O1DC、∠O1CD的平分线交于点O2称为第2次操作,作∠O2DC、∠O2CD的平分线交于点O3称为第3次操作,…,则第5次操作后∠CO5D的度数是 .
16.(4分)如图,在图(1)中,A1、B1、C1分别是△ABC的边BC、CA、AB的中点,在图(2)中,A2、B2、C2分别是△A1B1C1的边B1C1、C1A1、A1B1的中点,…,按此规律,则第n个图形中平行四边形的个数共有 个
三、综合题(共7题;共66分)
17.(6分)如图,点B、E、C、F在一条直线上,AB=DF,AC=DE,BE=FC.
(1)(3分)求证:△ABC≌△DFE;
(2)(3分)连接AF、BD,求证:四边形ABDF是平行四边形.
18.(8分)已知:平行四边形ABCD中,对角线AC、BD相交于点O.BD=2AD,E、F、G分别是OC、OD、AB的中点.
求证:
(1)(4分)BE⊥AC;
(2)(4分)EG=EF.
19.(8分)如图,已知,在 中,点D是边AC的中点,点E是边BC的延长线上一点,过点A作BE的平行线与线段ED的延长线相交于点F,连结AE.
(1)(4分)求证:AF=CE.
(2)(4分)连结CF,交边AB于点G,如果CF⊥AB,求证: .
20.(10分)如图,在平行四边形 中, 是 的中点,延长 到点 ,使 ,连结 ,
(1)(5分)求证:四边形 是平行四边形;
(2)(5分)若 , , ,求 的长.
21.(10分)如图,一块平行四边形场地ABCD,测得∠ABC=60°,AB=2,AD=4,AE⊥BD于点E,CF⊥BD于点F,连接CE,AF.现计划在四边形AECF区域内种植花草;
(1)(5分)求证:四边形AECF是平行四边形;
(2)(5分)求四边形AECF的面积.
22.(10分)如图,平行四边形ABCD中,点O是对角线AC的中点,点M为BC上一点,连接AM,且AB=AM,点E为BM中点,AF⊥AB,连接EF,延长FO交AB于点N.
(1)(5分)若BM=4,MC=3,AC= ,求AM的长度;
(2)(5分)若∠ACB=45°,求证:AN+AF= EF.
23.(14分)如图,在四边形ABCD中,AD∥BC,AD=12cm,BC=15cm,点P自点A向D以1cm/s的速度运动,到D点即停止.点Q自点C向B以2cm/s的速度运动,到B点即停止,点P,Q同时出发,设运动时间为t(s).
(1)(1分)用含t的代数式表示:
AP= ;DP= ;BQ= ;CQ= .
(2)(5分)当t为何值时,四边形APQB是平行四边形?
(3)(5分)当t为何值时,四边形PDCQ是平行四边形?
答案解析部分
1.【答案】C
2.【答案】C
3.【答案】C
4.【答案】C
5.【答案】B
6.【答案】D
7.【答案】B
8.【答案】D
9.【答案】B
10.【答案】C
11.【答案】30
12.【答案】72
13.【答案】6
14.【答案】10
15.【答案】175°
16.【答案】3n
17.【答案】(1)证明:∵BE=FC,
∴BC=EF,
在△ABC和△DFE中,
,
∴△ABC≌△DFE(SSS)
(2)解:由(1)知△ABC≌△DFE,
∴∠ABC=∠DFE,
∴AB∥DF,
∵AB=DF,
∴四边形ABDF是平行四边形.
18.【答案】(1)证明:∵四边形ABCD是平行四边形,
∴AD=BC,BD=2BO.
∵BD=2AD,
∴BO=BC,
又∵点E是OC中点,
∴BE⊥AC;
(2)证明:由(1)知BE⊥AC
又∵点G是AB中点,
∴EG是Rt△ABE斜边上的中线,
∴EG=AB,
又∵EF是△OCD的中位线,
∴EF=CD,
又∵AB=CD,
∴EG=EF.
19.【答案】(1)证明: 点D是边AC的中点,
,
,
,
在 和 中, ,
,
;
(2)解:由(1)知, ,
,
四边形AECF是平行四边形,
,
,
,
,
.
20.【答案】(1)证明: ∵DF=CE,且DF∥CE。 ∴四边形CEDF是平行四边形
(2)解:如图,过点D作DH⊥BE于点H,
∴在Rt△DHE中,根据勾股定理,得
21.【答案】(1)证明:∵四边形ABCD是平行四边形,
∴S△ABD=S△CBD,
∵AE⊥BD,CF⊥BD,
∴AE∥CF
∴AE BD= CF BD,
∴AE=CF,
∴四边形AECF是平行四边形
(2)解:过点B作BH⊥AD,交DA的延长线于点H,∵∠ABC=60°,
∴∠ABH=30°,
∵AB=2,
∴AH=1,BH= ,
∴DH=AH+AD=1+4=5,
∴BD= ,
∵S△ABD= BD AE= AD BH,
即 × ×AE= ×4× ,
解得:AE= ,
∴BE= ,
同理:DF=BE= ,
∴EF=BD﹣BE﹣DF= ,
∴S四边形AECF=EF AE=
22.【答案】(1)解:如图1中,连接AE.
∵AB=AM,BE=EM,
∴AE⊥BM,
在Rt△ACE中,∵AC= ,EC=EM+CM=5,
∴AE= = ,
在Rt△AEM中,AM= =
(2)解:如图,连接AE,作EH⊥AF于F,EG⊥DC交DC的延长线于E.
∵∠AEC=∠AFC=90°,
∴∠AEC+∠AFC=90°,
∴A,E,C,F四点共圆,
∴∠AFE=∠ACE=45°,
∴∠EFA=∠EFG=45°,
∵EH⊥FA,EG⊥FG,
∴EH=EG,
∵∠ACE=∠EAC=45°,
∴AE=EC,
∴Rt△EHA≌Rt△EGC(HL),
∴AH=CG,
∵EF=EF,EH=EG,
∴Rt△EHF≌Rt△EGF(HL),
∴FH=FG,
∵AB∥CD,
∴∠OAN=∠OCF,
∵∠AON=∠COF,OA=OC,
∴△AON≌△COF(ASA),
∴AN=CF,
∴AN+AF=FC+AF=FG﹣CG+FH+AH=2FH,
∵EF= FH,
∴AN+AF= EF
23.【答案】(1)t;12﹣t;15﹣2t;2t
(2)解:根据题意有AP=t,CQ=2t,PD=12﹣t,BQ=15﹣2t.
∵AD∥BC,∴当AP=BQ时,四边形APQB是平行四边形.
∴t=15﹣2t,解得t=5.
∴运动5s时四边形APQB是平行四边形
(3)解:由AP=tcm,CQ=2tcm,
∵AD=12cm,BC=15cm,
∴PD=AD﹣AP=12﹣t,
如图1当PQ∥CD,且PQ=CD时,
∵AD∥BC,即PD∥QC,
∴四边形PQCD为平行四边形,
∴PQ=CD,PD=CQ,
∴12﹣t=2t,
解得t=4s,
即当t=4s时,四边形PDCQ是平行四边形.
1 / 1
同课章节目录
- 第一章 二次根式
- 1.1 二次根式
- 1.2 二次根式的性质
- 1.3 二次根式的运算
- 第二章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程的应用
- 2.4 一元二次方程根与系数的关系(选学)
- 第三章 数据分析初步
- 3.1 平均数
- 3.2 中位数和众数
- 3.3 方差和标准差
- 第四章 平行四边形
- 4.1 多边形
- 4.2 平行四边形
- 4.3 中心对称
- 4.4 平行四边形的判定
- 4.5 三角形的中位线
- 4.6 反证法
- 第五章 特殊平行四边形
- 5.1 矩形
- 5.2 菱形
- 5.3 正方形
- 第六章 反比例函数
- 6.1 反比例函数
- 6.2 反比例函数的图象和性质
- 6.3 反比例函数的应用
