2021-2022学年浙教版数学8年级下学期 第五章 特殊平行四边形综合测评(含答案)
文档属性
| 名称 | 2021-2022学年浙教版数学8年级下学期 第五章 特殊平行四边形综合测评(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-03 21:33:06 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
2021-2022学年浙教版数学8年级下学期
第五章 特殊平行四边形 综合测评
一、单选题(共10题;共30分)
1.(3分)下列命题中,正确的命题是( )
A.两条对角线相等的四边形是矩形
B.两条角线互相垂直且相等的四边形是正方形
C.两条对角线相互垂直的四边形是菱形
D.两条对角线互相平分的四边形是平行四边形
2.(3分)如图,在菱形ABCD中,,点E,F分别在边AB,BC上,,的周长为,则AD的长为( )
A. B. C. D.
3.(3分)如图,P为AB上任意一点,分别以AP、PB为边在AB同侧作正方形APCD、正方形PBEF,设 ,则 为( )
A.2α B.90°﹣α
C.45°+α D.90°﹣ α
4.(3分)如图,在菱形ABCD中,∠B=60°,AB=1,延长AD到点E,使DE=AD,延长CD到点F,使DF=CD,连接AC、CE、EF、AF,则下列描述正确的是( )
A.四边形ACEF是平行四边形,它的周长是4
B.四边形ACEF是矩形,它的周长是2+2
C.四边形ACEF是平行四边形,它的周长是4
D.四边形ACEF是矩形,它的周长是4+4
5.(3分)如图,在△ABC中,点E,D,F分别在边AB,BC,CA上,且DE∥CA,DF∥BA.下列四个判断中,不正确的是( )
A.四边形AEDF是平行四边形
B.如果∠BAC=90°,那么四边形AEDF是矩形
C.如果AD平分∠BAC,那么四边形AEDF是菱形
D.如果AD⊥BC,那么四边形AEDF是菱形
6.(3分)正方形ABCD的边AB上有一动点E,以EC为边作矩形ECFG,且边FG过点D,在点E从点A移动到点B的过程中,矩形ECFG的面积( )
A.先变大后变小 B.先变小后变大
C.一直变大 D.保持不变
7.(3分)如图,已知正方形ABCD的边长为4,P是对角线BD上一点,PE⊥BC于点E,PF⊥CD于点F,连接AP,EF.给出下列结论:①PD= EC;②四边形PECF的周长为8;③△APD一定是等腰三角形;④AP=EF;⑤EF的最小值为2 ;⑥AP⊥EF.其中正确结论的序号为( )
A.①②④⑤⑥ B.①②④⑤ C.②④⑤ D.②④⑤⑥
8.(3分)如图,在△ABC中,∠ACB=90°,以△ABC的各边为边作三个正方形,点G落在HI上,若AC+BC=6,空白部分面积为10.5,则AB的长为( )
A.3 B. C.2 D.
9.(3分)如图,矩形ABCD的面积为1cm2,对角线交于点O;以AB、AO为邻边作平行四边形AOC1B,对角线交于点O1;以AB、AO1为邻边作平行四边形AO1C2B…;依此类推,则平行四边形AO2014C2015B的面积为( )
A. B. C. D.
10.(3分)如图,在正方形ABCD中,点P是AB上一动点(不与A,B重合),对角线AC,BD相交于点O,过点P分别作AC,BD的垂线,分别交AC,BD于点E,F,交AD,BC于点M,N.下列结论:①△APE≌△AME;②PM+PN=AC;③PE2+PF2=PO2;④△POF∽△BNF;⑤当△PMN∽△AMP时,点P是AB的中点.其中正确的结论的个数有( )个
A.5 B.4 C.3 D.2
二、填空题(共6题;共24分)
11.(4分)如图,在正方形ABCD的外侧,作等边△ADE,则∠AEB= .
12.(4分)如图,矩形ABCD的对角线AC与BD相交点O,AC=10,P、Q分别为AO、AD的中点,则PQ的的长度为 .
13.(4分)如图,矩形ABCD中,AD=6,CD=6+ ,E为AD上一点,且AE=2,点F,H分别在边AB,CD上,四边形EFGH为矩形,点G在矩形ABCD的内部,则当△BGC为直角三角形时,AF的值是 .
14.(4分)如图,在Rt△ABC中,∠BAC=900,且BA=3,AC=4,点D是斜边BC上的一个动点,过点D分别作DM⊥AB于点M,DN⊥AC于点N,连接MN,则线段MN的最小值为 .
15.(4分)如图,在边长为10的菱形 中,对角线 ,点O是线段 上的动点, 于E, 于F.则 .
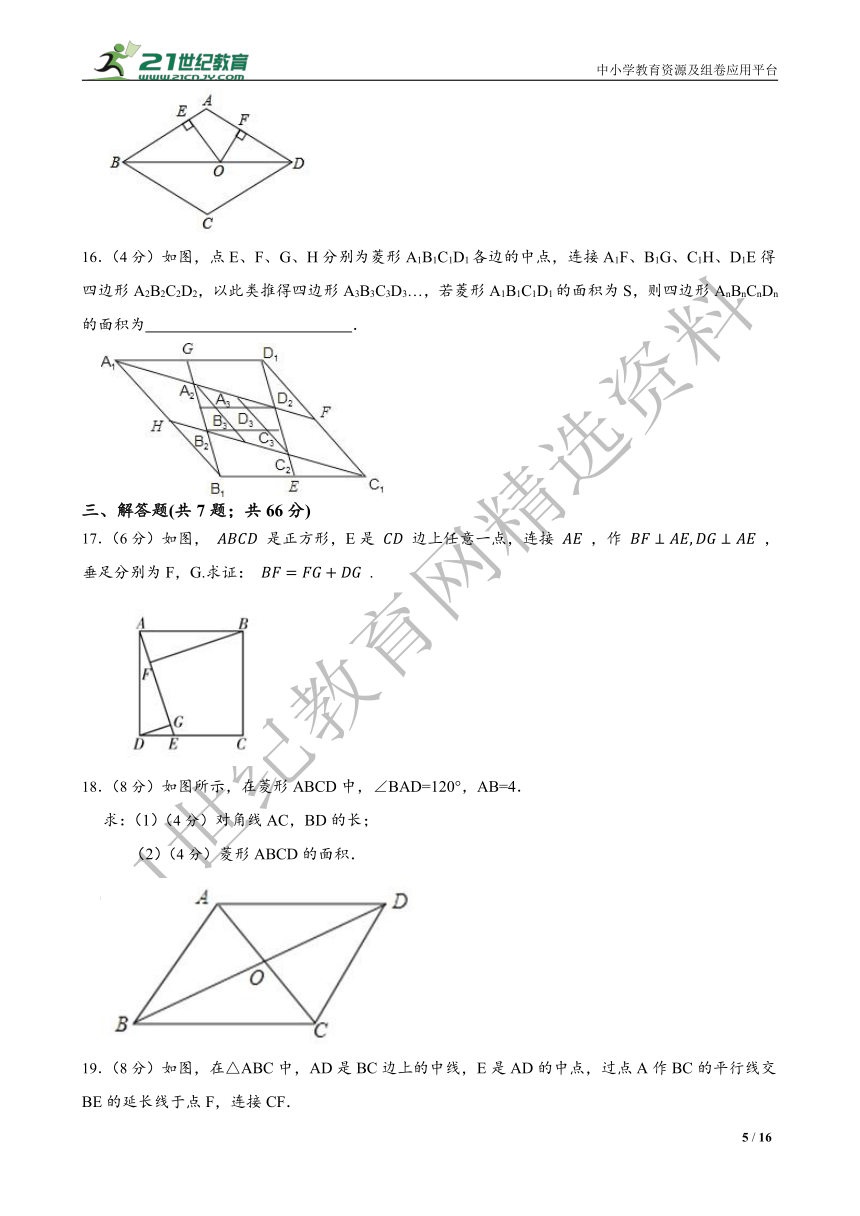
16.(4分)如图,点E、F、G、H分别为菱形A1B1C1D1各边的中点,连接A1F、B1G、C1H、D1E得四边形A2B2C2D2,以此类推得四边形A3B3C3D3…,若菱形A1B1C1D1的面积为S,则四边形AnBnCnDn的面积为 .
三、解答题(共7题;共66分)
17.(6分)如图, 是正方形,E是 边上任意一点,连接 ,作 ,垂足分别为F,G.求证: .
18.(8分)如图所示,在菱形ABCD中,∠BAD=120°,AB=4.
求:(1)(4分)对角线AC,BD的长;
(2)(4分)菱形ABCD的面积.
19.(8分)如图,在△ABC中,AD是BC边上的中线,E是AD的中点,过点A作BC的平行线交BE的延长线于点F,连接CF.
(1)(4分)求证:AF=DC;
(2)(4分)若AB⊥AC,试判断四边形ADCF的形状,并证明你的结论.
20.(8分)如图,在菱形ABCD中,对角线AC与BD相交于点O,MN过点O且与边AD、BC分别交于点M和点N.
(1)(4分)请你判断OM与ON的数量关系,并说明理由;
(2)(4分)过点D作DE∥AC交BC的延长线于E,当AB=5,AC=6时,求△BDE的周长.
21.(12分)如图,点G是正方形ABCD对角线CA的延长线上任意一点,以线段AG为边作一个正方形AEFG,线段EB和GD相交于点H.
(1)(4分)求证:EB=GD;
(2)(4分)判断EB与GD的位置关系,并说明理由;
(3)(4分)若AB=2,AG= ,求EB的长.
22.(12分)如图,在正方形ABCD中,AB=2,点P是边BC上的任意一点,E是BC延长线上一点,连结AP,作PFAP交DCE的平分线CF上一点F,连结AF交边CD于点G.
(1)(4分)求证:AP=PF;
(2)(4分)设点P到点B的距离为x,线段DG的长为y,试求y关于x的函数关系式,并写出自变量x的取值范围;
(3)(4分)当点P是线段BC延长线上一动点,那么(2)式中y与x的函数关系式保持不变吗?如改变,试直接写出函数关系式.
23.(12分)在平面直角坐标系中,O为原点,点A(6,0),点B在y轴的正半轴上,∠ABO=30°.矩形CODE的顶点D,E,C分别在OA,AB,OB上,OD=2.
(Ⅰ)(4分)如图①,求点E的坐标;
(Ⅱ)将矩形CODE沿x轴向右平移,得到矩形C′O′D′E′,点C,O,D,E的对应点分别为C′,O′,D′,E′.设OO′=t,矩形C′O′D′E′与△ABO重叠部分的面积为S.
(4分)如图②,当矩形C′O′D′E′与△ABO重叠部分为五边形时,C′E′,E′D′分别与AB相交于点M,F,试用含有t的式子表示S,并直接写出t的取值范围;
(4分)当 ≤S≤5 时,求t的取值范围(直接写出结果即可).
答案解析部分
1.【答案】D
2.【答案】C
3.【答案】B
4.【答案】B
5.【答案】D
6.【答案】D
7.【答案】A
8.【答案】B
9.【答案】C
10.【答案】B
11.【答案】15°
12.【答案】2.5
13.【答案】2或4
14.【答案】 (或2.4)
15.【答案】9.6
16.【答案】( )n﹣1S或
17.【答案】证明:∵四边形 是正方形,
∴ , ,
∵ ,
∴ ,
∵ ,
∴ ,
在 和 中,
∵
∴ ,
∴ , ,
∵
∴ .
18.【答案】解:(1)∵四边形ABCD是菱形,
∴AB=BC,
∵∠BAD=120°,
∴∠BAC=60°,
∴△ABC是等边三角形,
∴AC=AB=4,
∵四边形ABCD是菱形,
∴AC⊥BD,A0=2,
∴OD= ==2,
∴BD=4;
(2)面积为AC×BD=4=8.
19.【答案】(1)证明:∵AF∥BC,
∴∠AFE=∠DBE,
∵E是AD的中点,AD是BC边上的中线,
∴AE=DE,BD=CD,
在△AFE和△DBE中
∴△AFE≌△DBE(AAS),
∴AF=BD,
∴AF=DC.
(2)四边形ADCF是菱形,
证明:AF∥BC,AF=DC,
∴四边形ADCF是平行四边形,
∵AC⊥AB,AD是斜边BC的中线,
∴AD=BC=DC,
∴平行四边形ADCF是菱形.
20.【答案】解:(1)∵四边形ABCD是菱形,
∴AD∥BC,AO=OC,
∴=1,
∴OM=ON.
(2)∵四边形ABCD是菱形,
∴AC⊥BD,AD=BC=AB=5,
∴BO==4,
∴BD=2BO=8,
∵DE∥AC,AD∥CE,
∴四边形ACED是平行四边形,
∴DE=AC=6,
∴△BDE的周长是:
BD+DE+BE
=BD+AC+(BC+CE)
=8+6+(5+5)
=24
即△BDE的周长是24.
21.【答案】(1)证明:在△GAD和△EAB中,∠GAD=90°+∠EAD,∠EAB=90°+∠EAD
∴∠GAD=∠EAB,
∵四边形EFGA和四边形ABCD是正方形,
∴AG=AE,AB=AD,
在△GAD和△EAB中,
,
∴△GAD≌△EAB(SAS),
∴EB=GD;
(2)解:EB⊥GD.
理由如下:∵四边形ABCD是正方形,
∴∠DAB=90°,
∴∠AMB+∠ABM=90°,
又∵△AEB≌△AGD,
∴∠GDA=∠EBA,
∵∠HMD=∠AMB(对顶角相等),
∴∠HDM+∠DMH=∠AMB+∠ABM=90°,
∴∠DHM=180°﹣(∠HDM+∠DMH)=180°﹣90°=90°,
∴EB⊥GD.
(3)解:连接AC、BD,BD与AC交于点O,
∵四边形ABCD是正方形,
∴BD⊥CG,
∵AB=AD=2,在Rt△ABD中,DB= ,
在Rt△AOB中,OA=OB,AB=2,由勾股定理得:2AO2=22,
OA= ,
即OG=OA+AG= + =2 ,
∴EB=GD= .
22.【答案】(1)证明:(1)在边AB上截取线段AH,使AH=PC,连接PH,
由正方形ABCD,得B=BCD=D=90,AB=BC=AD,
∵APF=90,∴APF=B.
∵APC=B+BAP=APF+FPC,∴PAH=FPC.
又∵BCD=DCE=90,CF平分DCE,∴FCE=45.∴PCF=135.
又∵AB=BC,AH=PC,∴BH=BP,即得BPH=BHP=45.
∴AHP=135,即得AHP=PCF.
在AHP和PCF中,PAH=FPC,AH=PC,AHP=PCF,
∴AHP≌PCF,
∴AP=PF.
(2)解:在AD上取点N,令ND=DG,
∴NDG是等腰直角三角形.∴NG=DG=y,AN=2-y.
同理,PM=x,AM=2-x,
∵APM=45-PAM=NAG,PMA=ANG=135,
∴APM∽GAN.
∴,即.
整理,得.
(3)解:改变,.
考点:1.正方形的性质;2.等腰直角三角形的判定和性质;3.全等三角形的判定与性质;4.由实际问题列函数关系式.
23.【答案】解:解:(Ⅰ)∵点A(6,0),
∴OA=6,
∵OD=2,
∴AD=OA﹣OD=6﹣2=4,
∵四边形CODE是矩形,
∴DE∥OC,
∴∠AED=∠ABO=30°,
在Rt△AED中,AE=2AD=8,ED= = =4 ,
∵OD=2,
∴点E的坐标为(2,4 );
(Ⅱ)①由平移的性质得:O′D′=2,E′D′=4 ,ME′=OO′=t,D′E′∥O′C′∥OB,
∴∠E′FM=∠ABO=30°,
∴在Rt△MFE′中,MF=2ME′=2t,FE′= = = t,
∴S△MFE′= ME′ FE′= ×t× t= ,
∵S矩形C′O′D′E′=O′D′ E′D′=2×4 =8 ,
∴S=S矩形C′O′D′E′﹣S△MFE′=8 ﹣ ,
∴S=﹣ t2+8 ,其中t的取值范围是:0<t<2;
②当S= 时,如图③所示:
O'A=OA﹣OO'=6﹣t,
∵∠AO'F=90°,∠AFO'=∠ABO=30°,
∴O'F= O'A= (6﹣t)
∴S= (6﹣t)× (6﹣t)= ,
解得:t=6﹣ ,或t=6+ (舍去),
∴t=6﹣ ;当S=5 时,如图④所示:
O'A=6﹣t,D'A=6﹣t﹣2=4﹣t,
∴O'G= (6﹣t),D'F= (4﹣t),
∴S= [ (6﹣t)+ (4﹣t)]×2=5 ,
解得:t= ,
∴当 ≤S≤5 时,t的取值范围为 ≤t≤6﹣ .
1 / 1
2021-2022学年浙教版数学8年级下学期
第五章 特殊平行四边形 综合测评
一、单选题(共10题;共30分)
1.(3分)下列命题中,正确的命题是( )
A.两条对角线相等的四边形是矩形
B.两条角线互相垂直且相等的四边形是正方形
C.两条对角线相互垂直的四边形是菱形
D.两条对角线互相平分的四边形是平行四边形
2.(3分)如图,在菱形ABCD中,,点E,F分别在边AB,BC上,,的周长为,则AD的长为( )
A. B. C. D.
3.(3分)如图,P为AB上任意一点,分别以AP、PB为边在AB同侧作正方形APCD、正方形PBEF,设 ,则 为( )
A.2α B.90°﹣α
C.45°+α D.90°﹣ α
4.(3分)如图,在菱形ABCD中,∠B=60°,AB=1,延长AD到点E,使DE=AD,延长CD到点F,使DF=CD,连接AC、CE、EF、AF,则下列描述正确的是( )
A.四边形ACEF是平行四边形,它的周长是4
B.四边形ACEF是矩形,它的周长是2+2
C.四边形ACEF是平行四边形,它的周长是4
D.四边形ACEF是矩形,它的周长是4+4
5.(3分)如图,在△ABC中,点E,D,F分别在边AB,BC,CA上,且DE∥CA,DF∥BA.下列四个判断中,不正确的是( )
A.四边形AEDF是平行四边形
B.如果∠BAC=90°,那么四边形AEDF是矩形
C.如果AD平分∠BAC,那么四边形AEDF是菱形
D.如果AD⊥BC,那么四边形AEDF是菱形
6.(3分)正方形ABCD的边AB上有一动点E,以EC为边作矩形ECFG,且边FG过点D,在点E从点A移动到点B的过程中,矩形ECFG的面积( )
A.先变大后变小 B.先变小后变大
C.一直变大 D.保持不变
7.(3分)如图,已知正方形ABCD的边长为4,P是对角线BD上一点,PE⊥BC于点E,PF⊥CD于点F,连接AP,EF.给出下列结论:①PD= EC;②四边形PECF的周长为8;③△APD一定是等腰三角形;④AP=EF;⑤EF的最小值为2 ;⑥AP⊥EF.其中正确结论的序号为( )
A.①②④⑤⑥ B.①②④⑤ C.②④⑤ D.②④⑤⑥
8.(3分)如图,在△ABC中,∠ACB=90°,以△ABC的各边为边作三个正方形,点G落在HI上,若AC+BC=6,空白部分面积为10.5,则AB的长为( )
A.3 B. C.2 D.
9.(3分)如图,矩形ABCD的面积为1cm2,对角线交于点O;以AB、AO为邻边作平行四边形AOC1B,对角线交于点O1;以AB、AO1为邻边作平行四边形AO1C2B…;依此类推,则平行四边形AO2014C2015B的面积为( )
A. B. C. D.
10.(3分)如图,在正方形ABCD中,点P是AB上一动点(不与A,B重合),对角线AC,BD相交于点O,过点P分别作AC,BD的垂线,分别交AC,BD于点E,F,交AD,BC于点M,N.下列结论:①△APE≌△AME;②PM+PN=AC;③PE2+PF2=PO2;④△POF∽△BNF;⑤当△PMN∽△AMP时,点P是AB的中点.其中正确的结论的个数有( )个
A.5 B.4 C.3 D.2
二、填空题(共6题;共24分)
11.(4分)如图,在正方形ABCD的外侧,作等边△ADE,则∠AEB= .
12.(4分)如图,矩形ABCD的对角线AC与BD相交点O,AC=10,P、Q分别为AO、AD的中点,则PQ的的长度为 .
13.(4分)如图,矩形ABCD中,AD=6,CD=6+ ,E为AD上一点,且AE=2,点F,H分别在边AB,CD上,四边形EFGH为矩形,点G在矩形ABCD的内部,则当△BGC为直角三角形时,AF的值是 .
14.(4分)如图,在Rt△ABC中,∠BAC=900,且BA=3,AC=4,点D是斜边BC上的一个动点,过点D分别作DM⊥AB于点M,DN⊥AC于点N,连接MN,则线段MN的最小值为 .
15.(4分)如图,在边长为10的菱形 中,对角线 ,点O是线段 上的动点, 于E, 于F.则 .
16.(4分)如图,点E、F、G、H分别为菱形A1B1C1D1各边的中点,连接A1F、B1G、C1H、D1E得四边形A2B2C2D2,以此类推得四边形A3B3C3D3…,若菱形A1B1C1D1的面积为S,则四边形AnBnCnDn的面积为 .
三、解答题(共7题;共66分)
17.(6分)如图, 是正方形,E是 边上任意一点,连接 ,作 ,垂足分别为F,G.求证: .
18.(8分)如图所示,在菱形ABCD中,∠BAD=120°,AB=4.
求:(1)(4分)对角线AC,BD的长;
(2)(4分)菱形ABCD的面积.
19.(8分)如图,在△ABC中,AD是BC边上的中线,E是AD的中点,过点A作BC的平行线交BE的延长线于点F,连接CF.
(1)(4分)求证:AF=DC;
(2)(4分)若AB⊥AC,试判断四边形ADCF的形状,并证明你的结论.
20.(8分)如图,在菱形ABCD中,对角线AC与BD相交于点O,MN过点O且与边AD、BC分别交于点M和点N.
(1)(4分)请你判断OM与ON的数量关系,并说明理由;
(2)(4分)过点D作DE∥AC交BC的延长线于E,当AB=5,AC=6时,求△BDE的周长.
21.(12分)如图,点G是正方形ABCD对角线CA的延长线上任意一点,以线段AG为边作一个正方形AEFG,线段EB和GD相交于点H.
(1)(4分)求证:EB=GD;
(2)(4分)判断EB与GD的位置关系,并说明理由;
(3)(4分)若AB=2,AG= ,求EB的长.
22.(12分)如图,在正方形ABCD中,AB=2,点P是边BC上的任意一点,E是BC延长线上一点,连结AP,作PFAP交DCE的平分线CF上一点F,连结AF交边CD于点G.
(1)(4分)求证:AP=PF;
(2)(4分)设点P到点B的距离为x,线段DG的长为y,试求y关于x的函数关系式,并写出自变量x的取值范围;
(3)(4分)当点P是线段BC延长线上一动点,那么(2)式中y与x的函数关系式保持不变吗?如改变,试直接写出函数关系式.
23.(12分)在平面直角坐标系中,O为原点,点A(6,0),点B在y轴的正半轴上,∠ABO=30°.矩形CODE的顶点D,E,C分别在OA,AB,OB上,OD=2.
(Ⅰ)(4分)如图①,求点E的坐标;
(Ⅱ)将矩形CODE沿x轴向右平移,得到矩形C′O′D′E′,点C,O,D,E的对应点分别为C′,O′,D′,E′.设OO′=t,矩形C′O′D′E′与△ABO重叠部分的面积为S.
(4分)如图②,当矩形C′O′D′E′与△ABO重叠部分为五边形时,C′E′,E′D′分别与AB相交于点M,F,试用含有t的式子表示S,并直接写出t的取值范围;
(4分)当 ≤S≤5 时,求t的取值范围(直接写出结果即可).
答案解析部分
1.【答案】D
2.【答案】C
3.【答案】B
4.【答案】B
5.【答案】D
6.【答案】D
7.【答案】A
8.【答案】B
9.【答案】C
10.【答案】B
11.【答案】15°
12.【答案】2.5
13.【答案】2或4
14.【答案】 (或2.4)
15.【答案】9.6
16.【答案】( )n﹣1S或
17.【答案】证明:∵四边形 是正方形,
∴ , ,
∵ ,
∴ ,
∵ ,
∴ ,
在 和 中,
∵
∴ ,
∴ , ,
∵
∴ .
18.【答案】解:(1)∵四边形ABCD是菱形,
∴AB=BC,
∵∠BAD=120°,
∴∠BAC=60°,
∴△ABC是等边三角形,
∴AC=AB=4,
∵四边形ABCD是菱形,
∴AC⊥BD,A0=2,
∴OD= ==2,
∴BD=4;
(2)面积为AC×BD=4=8.
19.【答案】(1)证明:∵AF∥BC,
∴∠AFE=∠DBE,
∵E是AD的中点,AD是BC边上的中线,
∴AE=DE,BD=CD,
在△AFE和△DBE中
∴△AFE≌△DBE(AAS),
∴AF=BD,
∴AF=DC.
(2)四边形ADCF是菱形,
证明:AF∥BC,AF=DC,
∴四边形ADCF是平行四边形,
∵AC⊥AB,AD是斜边BC的中线,
∴AD=BC=DC,
∴平行四边形ADCF是菱形.
20.【答案】解:(1)∵四边形ABCD是菱形,
∴AD∥BC,AO=OC,
∴=1,
∴OM=ON.
(2)∵四边形ABCD是菱形,
∴AC⊥BD,AD=BC=AB=5,
∴BO==4,
∴BD=2BO=8,
∵DE∥AC,AD∥CE,
∴四边形ACED是平行四边形,
∴DE=AC=6,
∴△BDE的周长是:
BD+DE+BE
=BD+AC+(BC+CE)
=8+6+(5+5)
=24
即△BDE的周长是24.
21.【答案】(1)证明:在△GAD和△EAB中,∠GAD=90°+∠EAD,∠EAB=90°+∠EAD
∴∠GAD=∠EAB,
∵四边形EFGA和四边形ABCD是正方形,
∴AG=AE,AB=AD,
在△GAD和△EAB中,
,
∴△GAD≌△EAB(SAS),
∴EB=GD;
(2)解:EB⊥GD.
理由如下:∵四边形ABCD是正方形,
∴∠DAB=90°,
∴∠AMB+∠ABM=90°,
又∵△AEB≌△AGD,
∴∠GDA=∠EBA,
∵∠HMD=∠AMB(对顶角相等),
∴∠HDM+∠DMH=∠AMB+∠ABM=90°,
∴∠DHM=180°﹣(∠HDM+∠DMH)=180°﹣90°=90°,
∴EB⊥GD.
(3)解:连接AC、BD,BD与AC交于点O,
∵四边形ABCD是正方形,
∴BD⊥CG,
∵AB=AD=2,在Rt△ABD中,DB= ,
在Rt△AOB中,OA=OB,AB=2,由勾股定理得:2AO2=22,
OA= ,
即OG=OA+AG= + =2 ,
∴EB=GD= .
22.【答案】(1)证明:(1)在边AB上截取线段AH,使AH=PC,连接PH,
由正方形ABCD,得B=BCD=D=90,AB=BC=AD,
∵APF=90,∴APF=B.
∵APC=B+BAP=APF+FPC,∴PAH=FPC.
又∵BCD=DCE=90,CF平分DCE,∴FCE=45.∴PCF=135.
又∵AB=BC,AH=PC,∴BH=BP,即得BPH=BHP=45.
∴AHP=135,即得AHP=PCF.
在AHP和PCF中,PAH=FPC,AH=PC,AHP=PCF,
∴AHP≌PCF,
∴AP=PF.
(2)解:在AD上取点N,令ND=DG,
∴NDG是等腰直角三角形.∴NG=DG=y,AN=2-y.
同理,PM=x,AM=2-x,
∵APM=45-PAM=NAG,PMA=ANG=135,
∴APM∽GAN.
∴,即.
整理,得.
(3)解:改变,.
考点:1.正方形的性质;2.等腰直角三角形的判定和性质;3.全等三角形的判定与性质;4.由实际问题列函数关系式.
23.【答案】解:解:(Ⅰ)∵点A(6,0),
∴OA=6,
∵OD=2,
∴AD=OA﹣OD=6﹣2=4,
∵四边形CODE是矩形,
∴DE∥OC,
∴∠AED=∠ABO=30°,
在Rt△AED中,AE=2AD=8,ED= = =4 ,
∵OD=2,
∴点E的坐标为(2,4 );
(Ⅱ)①由平移的性质得:O′D′=2,E′D′=4 ,ME′=OO′=t,D′E′∥O′C′∥OB,
∴∠E′FM=∠ABO=30°,
∴在Rt△MFE′中,MF=2ME′=2t,FE′= = = t,
∴S△MFE′= ME′ FE′= ×t× t= ,
∵S矩形C′O′D′E′=O′D′ E′D′=2×4 =8 ,
∴S=S矩形C′O′D′E′﹣S△MFE′=8 ﹣ ,
∴S=﹣ t2+8 ,其中t的取值范围是:0<t<2;
②当S= 时,如图③所示:
O'A=OA﹣OO'=6﹣t,
∵∠AO'F=90°,∠AFO'=∠ABO=30°,
∴O'F= O'A= (6﹣t)
∴S= (6﹣t)× (6﹣t)= ,
解得:t=6﹣ ,或t=6+ (舍去),
∴t=6﹣ ;当S=5 时,如图④所示:
O'A=6﹣t,D'A=6﹣t﹣2=4﹣t,
∴O'G= (6﹣t),D'F= (4﹣t),
∴S= [ (6﹣t)+ (4﹣t)]×2=5 ,
解得:t= ,
∴当 ≤S≤5 时,t的取值范围为 ≤t≤6﹣ .
1 / 1
同课章节目录
- 第一章 二次根式
- 1.1 二次根式
- 1.2 二次根式的性质
- 1.3 二次根式的运算
- 第二章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程的应用
- 2.4 一元二次方程根与系数的关系(选学)
- 第三章 数据分析初步
- 3.1 平均数
- 3.2 中位数和众数
- 3.3 方差和标准差
- 第四章 平行四边形
- 4.1 多边形
- 4.2 平行四边形
- 4.3 中心对称
- 4.4 平行四边形的判定
- 4.5 三角形的中位线
- 4.6 反证法
- 第五章 特殊平行四边形
- 5.1 矩形
- 5.2 菱形
- 5.3 正方形
- 第六章 反比例函数
- 6.1 反比例函数
- 6.2 反比例函数的图象和性质
- 6.3 反比例函数的应用
