4.3.1两个三角形相似的判定(一)
图片预览
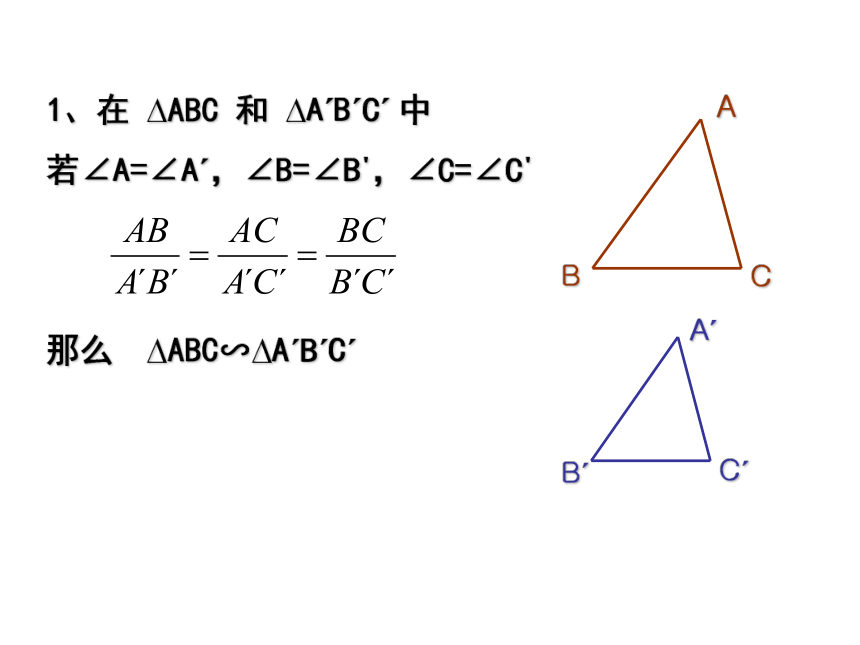
文档简介
课件14张PPT。4.1.3 两个三角形相似的判定(一)1、在 ?ABC 和 ?A?B?C? 中
若∠A=∠A?,∠B=∠B?,∠C=∠C?
那么 ?ABC∽?A?B?C?
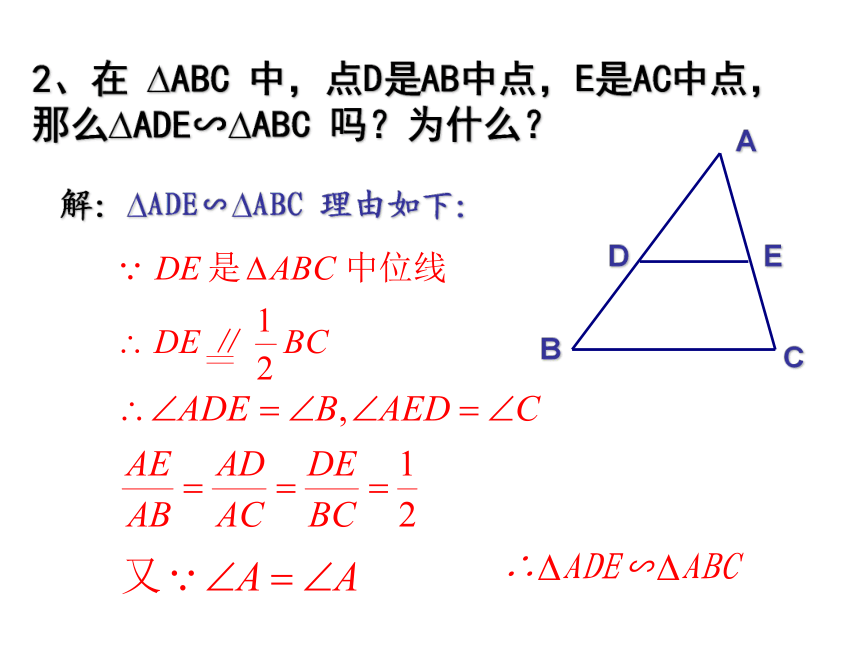
解:?ADE∽?ABC 理由如下:2、在 ?ABC 中,点D是AB中点,E是AC中点,那么?ADE∽?ABC 吗?为什么?ADCBE∴?ADE∽?ABC3、在 ?ABC 中,D在AB上,E在AC上,
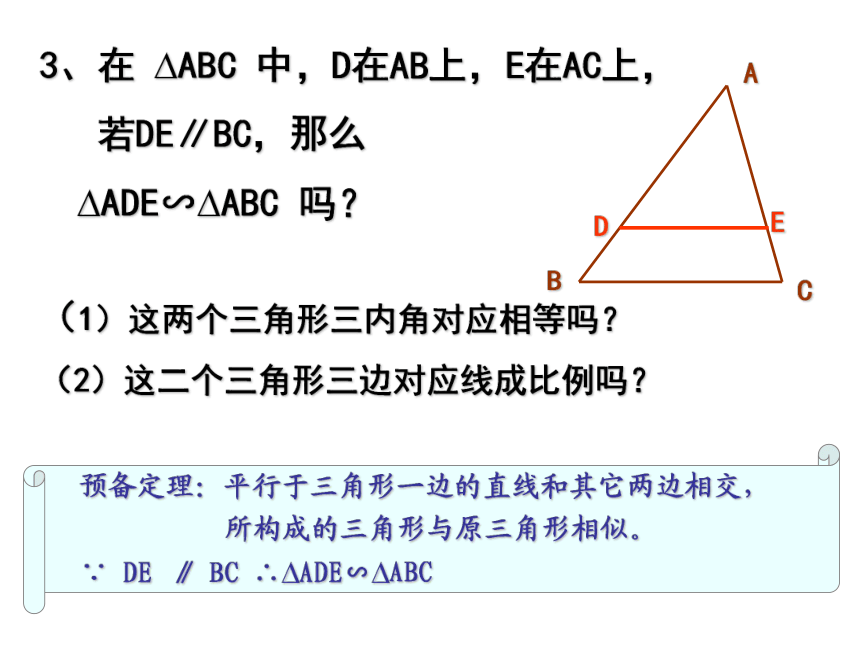
若DE∥BC,那么
?ADE∽?ABC 吗?
(1)这两个三角形三内角对应相等吗?
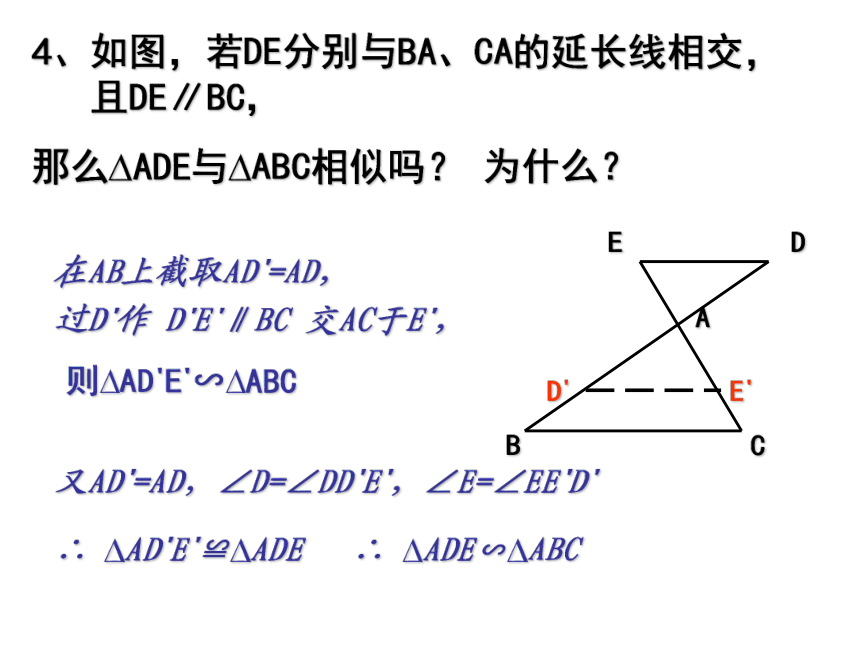
(2)这二个三角形三边对应线成比例吗?预备定理:平行于三角形一边的直线和其它两边相交, 所构成的三角形与原三角形相似。 ∵ DE ∥ BC ∴?ADE∽?ABC 4、如图,若DE分别与BA、CA的延长线相交, 且DE∥BC,
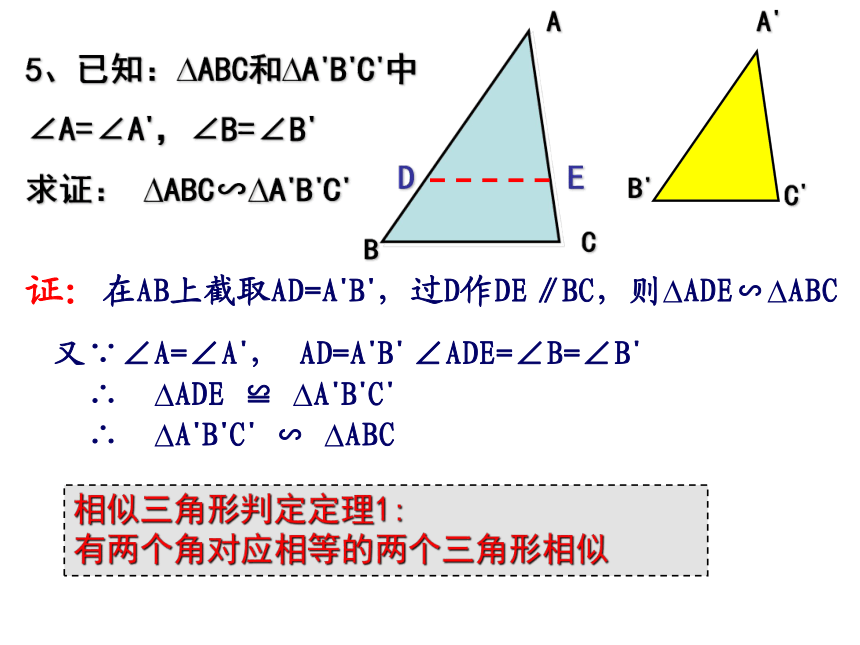
那么?ADE与?ABC相似吗? 为什么?在AB上截取AD?=AD, 过D?作 D?E?∥BC 交AC于E?,A BCDED?E?又AD?=AD,∠D=∠DD?E?,∠E=∠EE?D?∴ ?AD?E?≌?ADE ∴ ?ADE∽?ABC则?AD?E?∽?ABC5、已知:?ABC和?A?B?C?中
∠A=∠A?,∠B=∠B?
求证: ?ABC∽?A?B?C?又∵∠A=∠A?, AD=A?B?∴ ?ADE ≌ ?A?B?C? 证:在AB上截取AD=A?B?,过D作DE∥BC,则?ADE∽?ABC∠ADE=∠B=∠B?∴ ?A?B?C? ∽ ?ABC ABCA?B?C?相似三角形判定定理1:
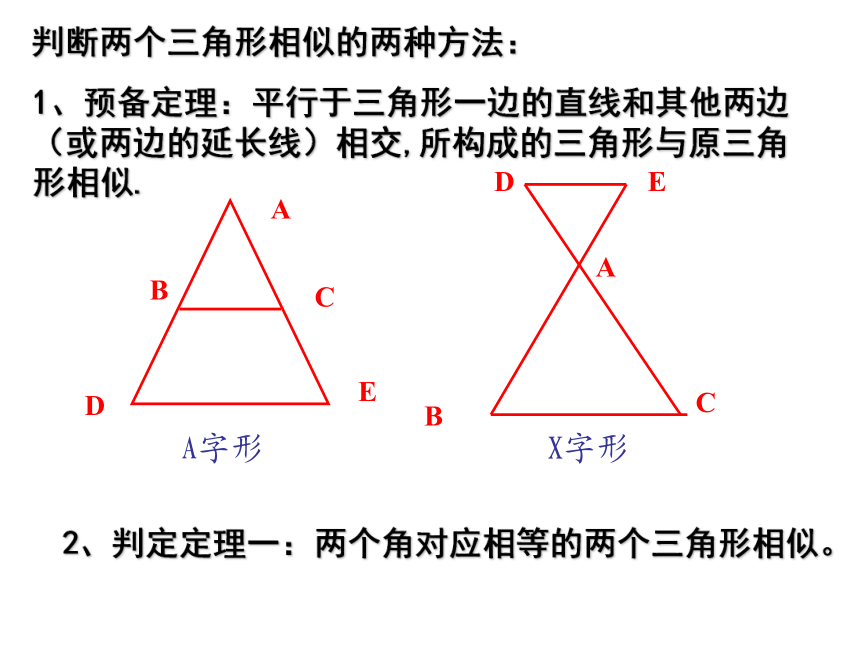
有两个角对应相等的两个三角形相似判断两个三角形相似的两种方法:
1、预备定理:平行于三角形一边的直线和其他两边(或两边的延长线)相交,所构成的三角形与原三角形相似.A字形X字形2、判定定理一:两个角对应相等的两个三角形相似。练习(1)如图 ?ABC和?DEF,∠A=40°,∠B=∠E=80°,∠F=60°?ABC与?DEF相似吗?为什么?(2)如图:DE∥BC, DF∥AC请找出所有相似三角形。例1 在一次数学活动课上,为了测量河宽AB,张杰采用了如下方法:从A处沿与AB垂直的直线方向走40M到达C处,插一根标杆,然后沿同方向继续走15M到达D处,再右转90度走到E处,使B,C,E三点恰好在一条直线上,量得DE=20M,这样就可以求出河宽AB.请你算出结果(要求给出解题过程) 例2 如图:?ABC中,∠ACB=90°,CD⊥AB于D,
请找出图中所有的相似三角形,并说明理由。AABCD解: ?ADC ∽ ?CDB ∽ ?ACB∵∠A=∠A ,∠ADC=∠ACB=90°∴ ?ADC ∽ ?ACB同理 ∠B=∠B ,∠BDC=∠BCA=90°∴ ?BDC ∽ ? BCA∴ ?ADC ∽ ? CDB ∽ ? ACB此结论可以称为“母子相似定理”,今后可以直接使用.延伸练习已知:如图,在ΔABC中,AD、BE分别是BC、AC上的高,AD、BE相交于点F。(2)图中还有与ΔAEF相似的三角形吗?请一一写出 。(1)求证:ΔAEF∽ΔADC;答:有ΔAEF∽ΔADC∽ΔBEC∽ΔBDF.1、三角形相似的判定方法
(1)平行于三角形一边的直线和其它两边相交,所构成的三角形与原三角形相似;
(2)有两个角对应相等的三角形相似。
2、母子相似三角形
Rt△被斜边上的高分成的二个直角三角形与原三角形相似。
小 结思考题: 书本P109.
B 组 第5题,第6题课件14张PPT。4.1.3 两个三角形相似的判定(一)1、在 ?ABC 和 ?A?B?C? 中
若∠A=∠A?,∠B=∠B?,∠C=∠C?
那么 ?ABC∽?A?B?C?
解:?ADE∽?ABC 理由如下:2、在 ?ABC 中,点D是AB中点,E是AC中点,那么?ADE∽?ABC 吗?为什么?ADCBE∴?ADE∽?ABC3、在 ?ABC 中,D在AB上,E在AC上,
若DE∥BC,那么
?ADE∽?ABC 吗?
(1)这两个三角形三内角对应相等吗?
(2)这二个三角形三边对应线成比例吗?预备定理:平行于三角形一边的直线和其它两边相交, 所构成的三角形与原三角形相似。 ∵ DE ∥ BC ∴?ADE∽?ABC 4、如图,若DE分别与BA、CA的延长线相交, 且DE∥BC,
那么?ADE与?ABC相似吗? 为什么?在AB上截取AD?=AD, 过D?作 D?E?∥BC 交AC于E?,A BCDED?E?又AD?=AD,∠D=∠DD?E?,∠E=∠EE?D?∴ ?AD?E?≌?ADE ∴ ?ADE∽?ABC则?AD?E?∽?ABC5、已知:?ABC和?A?B?C?中
∠A=∠A?,∠B=∠B?
求证: ?ABC∽?A?B?C?又∵∠A=∠A?, AD=A?B?∴ ?ADE ≌ ?A?B?C? 证:在AB上截取AD=A?B?,过D作DE∥BC,则?ADE∽?ABC∠ADE=∠B=∠B?∴ ?A?B?C? ∽ ?ABC ABCA?B?C?相似三角形判定定理1:
有两个角对应相等的两个三角形相似判断两个三角形相似的两种方法:
1、预备定理:平行于三角形一边的直线和其他两边(或两边的延长线)相交,所构成的三角形与原三角形相似.A字形X字形2、判定定理一:两个角对应相等的两个三角形相似。练习(1)如图 ?ABC和?DEF,∠A=40°,∠B=∠E=80°,∠F=60°?ABC与?DEF相似吗?为什么?(2)如图:DE∥BC, DF∥AC请找出所有相似三角形。例1 在一次数学活动课上,为了测量河宽AB,张杰采用了如下方法:从A处沿与AB垂直的直线方向走40M到达C处,插一根标杆,然后沿同方向继续走15M到达D处,再右转90度走到E处,使B,C,E三点恰好在一条直线上,量得DE=20M,这样就可以求出河宽AB.请你算出结果(要求给出解题过程) 例2 如图:?ABC中,∠ACB=90°,CD⊥AB于D,
请找出图中所有的相似三角形,并说明理由。AABCD解: ?ADC ∽ ?CDB ∽ ?ACB∵∠A=∠A ,∠ADC=∠ACB=90°∴ ?ADC ∽ ?ACB同理 ∠B=∠B ,∠BDC=∠BCA=90°∴ ?BDC ∽ ? BCA∴ ?ADC ∽ ? CDB ∽ ? ACB此结论可以称为“母子相似定理”,今后可以直接使用.延伸练习已知:如图,在ΔABC中,AD、BE分别是BC、AC上的高,AD、BE相交于点F。(2)图中还有与ΔAEF相似的三角形吗?请一一写出 。(1)求证:ΔAEF∽ΔADC;答:有ΔAEF∽ΔADC∽ΔBEC∽ΔBDF.1、三角形相似的判定方法
(1)平行于三角形一边的直线和其它两边相交,所构成的三角形与原三角形相似;
(2)有两个角对应相等的三角形相似。
2、母子相似三角形
Rt△被斜边上的高分成的二个直角三角形与原三角形相似。
小 结思考题: 书本P109.
B 组 第5题,第6题
若∠A=∠A?,∠B=∠B?,∠C=∠C?
那么 ?ABC∽?A?B?C?
解:?ADE∽?ABC 理由如下:2、在 ?ABC 中,点D是AB中点,E是AC中点,那么?ADE∽?ABC 吗?为什么?ADCBE∴?ADE∽?ABC3、在 ?ABC 中,D在AB上,E在AC上,
若DE∥BC,那么
?ADE∽?ABC 吗?
(1)这两个三角形三内角对应相等吗?
(2)这二个三角形三边对应线成比例吗?预备定理:平行于三角形一边的直线和其它两边相交, 所构成的三角形与原三角形相似。 ∵ DE ∥ BC ∴?ADE∽?ABC 4、如图,若DE分别与BA、CA的延长线相交, 且DE∥BC,
那么?ADE与?ABC相似吗? 为什么?在AB上截取AD?=AD, 过D?作 D?E?∥BC 交AC于E?,A BCDED?E?又AD?=AD,∠D=∠DD?E?,∠E=∠EE?D?∴ ?AD?E?≌?ADE ∴ ?ADE∽?ABC则?AD?E?∽?ABC5、已知:?ABC和?A?B?C?中
∠A=∠A?,∠B=∠B?
求证: ?ABC∽?A?B?C?又∵∠A=∠A?, AD=A?B?∴ ?ADE ≌ ?A?B?C? 证:在AB上截取AD=A?B?,过D作DE∥BC,则?ADE∽?ABC∠ADE=∠B=∠B?∴ ?A?B?C? ∽ ?ABC ABCA?B?C?相似三角形判定定理1:
有两个角对应相等的两个三角形相似判断两个三角形相似的两种方法:
1、预备定理:平行于三角形一边的直线和其他两边(或两边的延长线)相交,所构成的三角形与原三角形相似.A字形X字形2、判定定理一:两个角对应相等的两个三角形相似。练习(1)如图 ?ABC和?DEF,∠A=40°,∠B=∠E=80°,∠F=60°?ABC与?DEF相似吗?为什么?(2)如图:DE∥BC, DF∥AC请找出所有相似三角形。例1 在一次数学活动课上,为了测量河宽AB,张杰采用了如下方法:从A处沿与AB垂直的直线方向走40M到达C处,插一根标杆,然后沿同方向继续走15M到达D处,再右转90度走到E处,使B,C,E三点恰好在一条直线上,量得DE=20M,这样就可以求出河宽AB.请你算出结果(要求给出解题过程) 例2 如图:?ABC中,∠ACB=90°,CD⊥AB于D,
请找出图中所有的相似三角形,并说明理由。AABCD解: ?ADC ∽ ?CDB ∽ ?ACB∵∠A=∠A ,∠ADC=∠ACB=90°∴ ?ADC ∽ ?ACB同理 ∠B=∠B ,∠BDC=∠BCA=90°∴ ?BDC ∽ ? BCA∴ ?ADC ∽ ? CDB ∽ ? ACB此结论可以称为“母子相似定理”,今后可以直接使用.延伸练习已知:如图,在ΔABC中,AD、BE分别是BC、AC上的高,AD、BE相交于点F。(2)图中还有与ΔAEF相似的三角形吗?请一一写出 。(1)求证:ΔAEF∽ΔADC;答:有ΔAEF∽ΔADC∽ΔBEC∽ΔBDF.1、三角形相似的判定方法
(1)平行于三角形一边的直线和其它两边相交,所构成的三角形与原三角形相似;
(2)有两个角对应相等的三角形相似。
2、母子相似三角形
Rt△被斜边上的高分成的二个直角三角形与原三角形相似。
小 结思考题: 书本P109.
B 组 第5题,第6题课件14张PPT。4.1.3 两个三角形相似的判定(一)1、在 ?ABC 和 ?A?B?C? 中
若∠A=∠A?,∠B=∠B?,∠C=∠C?
那么 ?ABC∽?A?B?C?
解:?ADE∽?ABC 理由如下:2、在 ?ABC 中,点D是AB中点,E是AC中点,那么?ADE∽?ABC 吗?为什么?ADCBE∴?ADE∽?ABC3、在 ?ABC 中,D在AB上,E在AC上,
若DE∥BC,那么
?ADE∽?ABC 吗?
(1)这两个三角形三内角对应相等吗?
(2)这二个三角形三边对应线成比例吗?预备定理:平行于三角形一边的直线和其它两边相交, 所构成的三角形与原三角形相似。 ∵ DE ∥ BC ∴?ADE∽?ABC 4、如图,若DE分别与BA、CA的延长线相交, 且DE∥BC,
那么?ADE与?ABC相似吗? 为什么?在AB上截取AD?=AD, 过D?作 D?E?∥BC 交AC于E?,A BCDED?E?又AD?=AD,∠D=∠DD?E?,∠E=∠EE?D?∴ ?AD?E?≌?ADE ∴ ?ADE∽?ABC则?AD?E?∽?ABC5、已知:?ABC和?A?B?C?中
∠A=∠A?,∠B=∠B?
求证: ?ABC∽?A?B?C?又∵∠A=∠A?, AD=A?B?∴ ?ADE ≌ ?A?B?C? 证:在AB上截取AD=A?B?,过D作DE∥BC,则?ADE∽?ABC∠ADE=∠B=∠B?∴ ?A?B?C? ∽ ?ABC ABCA?B?C?相似三角形判定定理1:
有两个角对应相等的两个三角形相似判断两个三角形相似的两种方法:
1、预备定理:平行于三角形一边的直线和其他两边(或两边的延长线)相交,所构成的三角形与原三角形相似.A字形X字形2、判定定理一:两个角对应相等的两个三角形相似。练习(1)如图 ?ABC和?DEF,∠A=40°,∠B=∠E=80°,∠F=60°?ABC与?DEF相似吗?为什么?(2)如图:DE∥BC, DF∥AC请找出所有相似三角形。例1 在一次数学活动课上,为了测量河宽AB,张杰采用了如下方法:从A处沿与AB垂直的直线方向走40M到达C处,插一根标杆,然后沿同方向继续走15M到达D处,再右转90度走到E处,使B,C,E三点恰好在一条直线上,量得DE=20M,这样就可以求出河宽AB.请你算出结果(要求给出解题过程) 例2 如图:?ABC中,∠ACB=90°,CD⊥AB于D,
请找出图中所有的相似三角形,并说明理由。AABCD解: ?ADC ∽ ?CDB ∽ ?ACB∵∠A=∠A ,∠ADC=∠ACB=90°∴ ?ADC ∽ ?ACB同理 ∠B=∠B ,∠BDC=∠BCA=90°∴ ?BDC ∽ ? BCA∴ ?ADC ∽ ? CDB ∽ ? ACB此结论可以称为“母子相似定理”,今后可以直接使用.延伸练习已知:如图,在ΔABC中,AD、BE分别是BC、AC上的高,AD、BE相交于点F。(2)图中还有与ΔAEF相似的三角形吗?请一一写出 。(1)求证:ΔAEF∽ΔADC;答:有ΔAEF∽ΔADC∽ΔBEC∽ΔBDF.1、三角形相似的判定方法
(1)平行于三角形一边的直线和其它两边相交,所构成的三角形与原三角形相似;
(2)有两个角对应相等的三角形相似。
2、母子相似三角形
Rt△被斜边上的高分成的二个直角三角形与原三角形相似。
小 结思考题: 书本P109.
B 组 第5题,第6题
同课章节目录
