4.3.2两个三角形相似的判定（二）

课件14张PPT。4.3.2 两个三角形相似的判定(二)
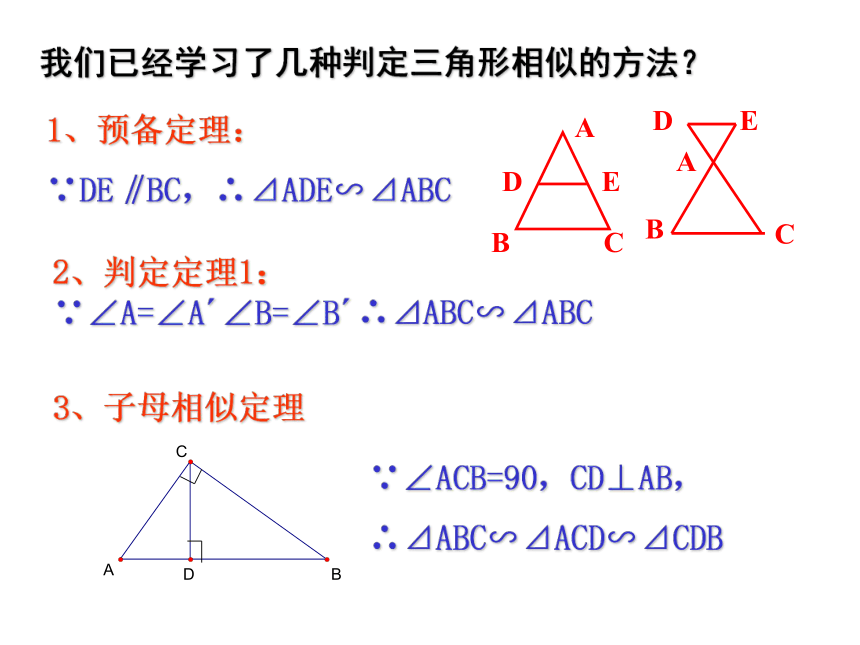
我们已经学习了几种判定三角形相似的方法？1、预备定理：
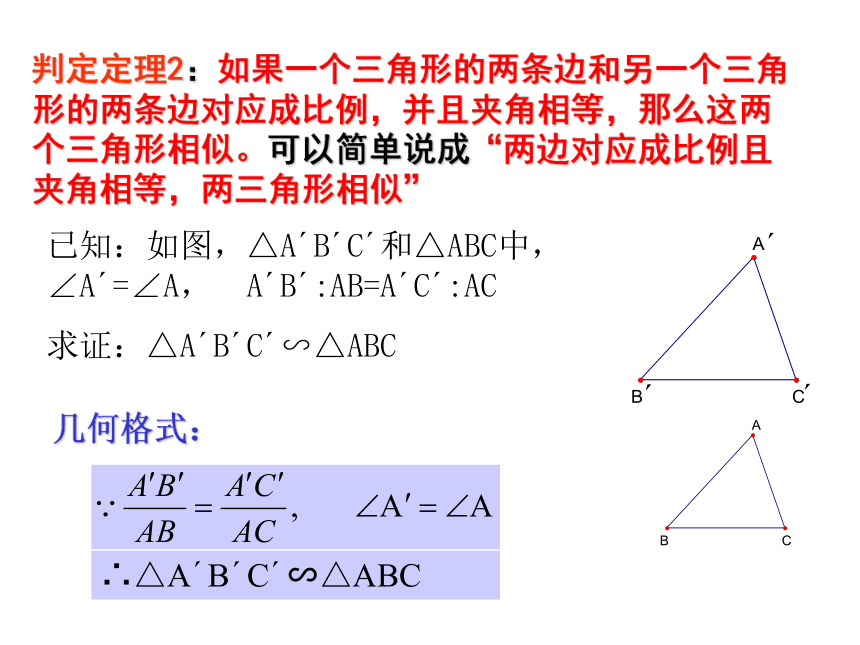
∵DE‖BC，∴⊿ADE∽⊿ABC2、判定定理1： ∵∠A=∠A′∠B=∠B′∴⊿ABC∽⊿ABC 判定定理2：如果一个三角形的两条边和另一个三角形的两条边对应成比例，并且夹角相等，那么这两个三角形相似。可以简单说成“两边对应成比例且夹角相等，两三角形相似”已知：如图，△A′B′C′和△ABC中， ∠A′=∠A， A′B′:AB=A′C′:AC
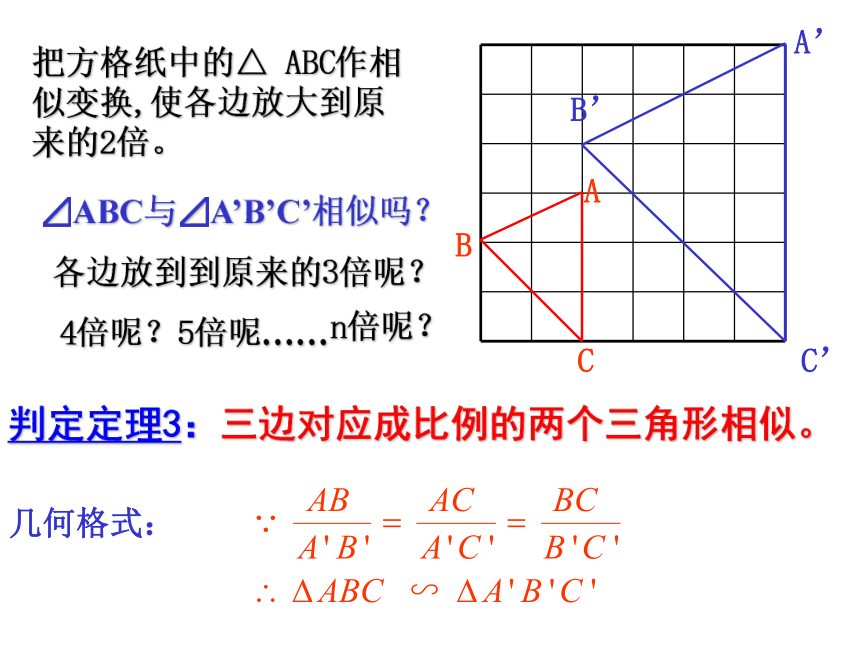
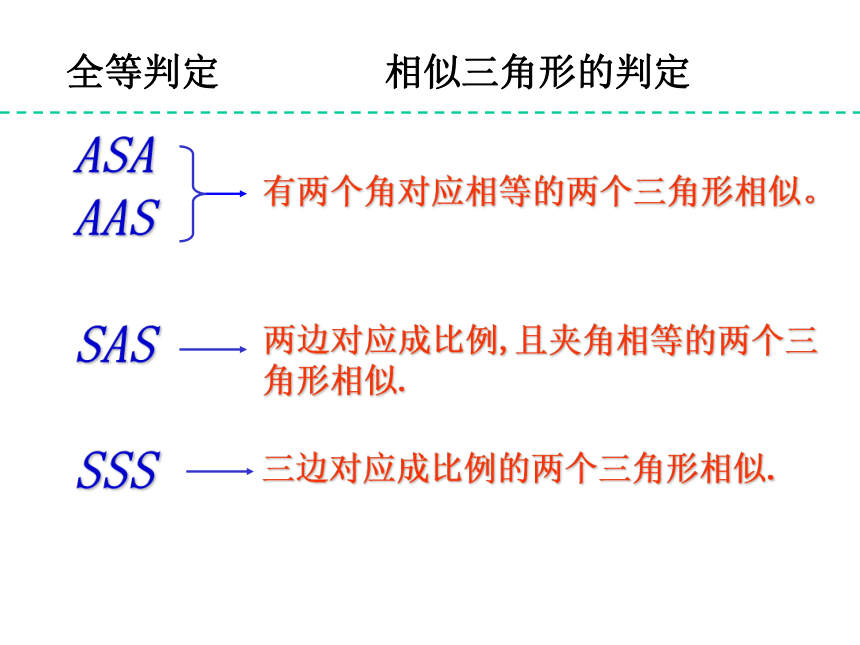
求证：△A′B′C′∽△ABC几何格式：∴△A′B′C′∽△ABC把方格纸中的△ ABC作相似变换,使各边放大到原来的2倍。判定定理3：三边对应成比例的两个三角形相似。⊿ABC与⊿A’B’C’相似吗？各边放到到原来的3倍呢？4倍呢？5倍呢……n倍呢？几何格式： 全等判定ASA
AAS
SAS
SSS 相似三角形的判定热身练习1：判断满足以下条件的两个三角形是否相似。⑴ BC=6厘米， AB=4厘米， AC=8厘米，
DE=12厘米，EF=18厘米，DF=24厘米
⑵ ∠A=120o，AB=7厘米，AC=14厘米，
∠B′=120o，A′B′=3厘米，A′C′=6厘米；
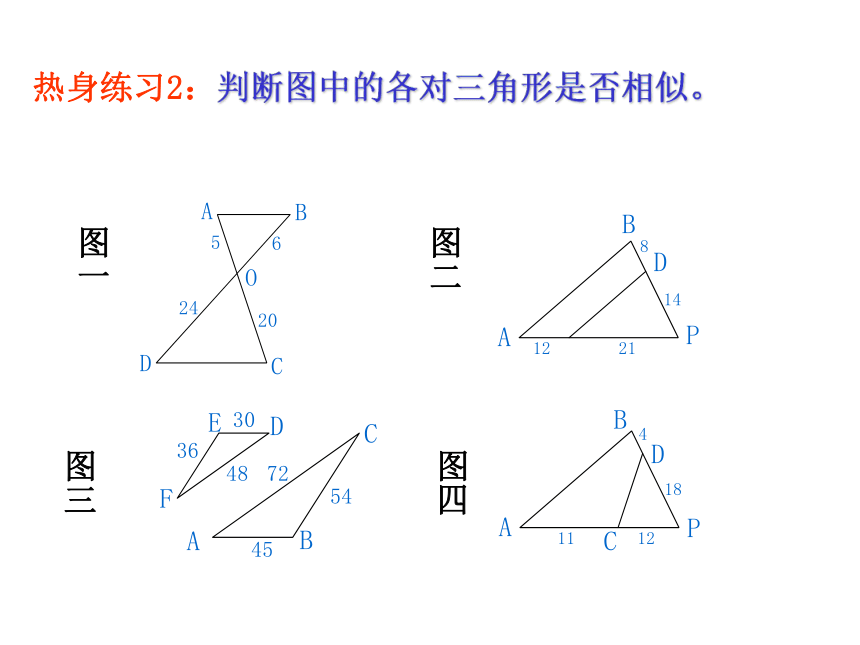
热身练习2：判断图中的各对三角形是否相似。图一图二图三图四求证:DE∥BC例1、如图,已知点D,E分别在AB,AC上,且证明：∵∠A=∠A∴△ABC∽△ADE∴ ∠ADE=∠B∴ DE∥BC方法一：设小正方形的边长为1，则比较容易计算三边的长度，然后寻找三边的对应关系；方法二：仔细观察不难发现图中的∠BAC和∠DEF都是直角，那么能否从两边一夹角的角度考虑并证明。例2、如图判断4×4方格中的两个三角形是否相似,并说明理由.EDFBAC例3、如图，D为△ABC的边AC上一点，若要使
△ABD与△ACB相似，可以添加一个什么条件？你有几种添加条件的不同方法？ABC在直角梯形BACD中,AC⊥CD,AC=CD=4AB, E是AC中点.变式练习:若AB=2,E是线段AC上的一个动点, △ABE与△CED相似,求AE的长.练一练(1)求证:△ABE∽△CED
(2)图中还有相似的三角形吗？(1)当CH为多少时，△ADE与以G、C、H为顶点的三角形相似．　　　如图：正方形ABCD的边长为２，DE＝EC，GH= ，线段GH的两端在BC与CD上滑动.拓展提高(2)当△ADE与以G、C、H为顶点的三角形相似时．连接AG,AH.图中还有哪些三角形相似？　　　几何画板演示知识的积累要多整理与小结相似三角形的判定方法共有哪些？2、平行于三角形一边的判定方法3、有两个角对应相等的判定方法 4、有两边对应生比例且夹角想相等的判定方法 5、有三边对应成比例的判定方法 温馨提示：
当我们在应用这些判定方法解题的时候一定要做正确的选择！1、根据定义判定6、直角三角形子母相似的判定方法K字型ABDEC条件∠A=∠B=Rt∠
AD:BC=AC:BE