4.4.1相似三角形性质应用一
图片预览


文档简介
课件22张PPT。4.4 相似三角形的性质
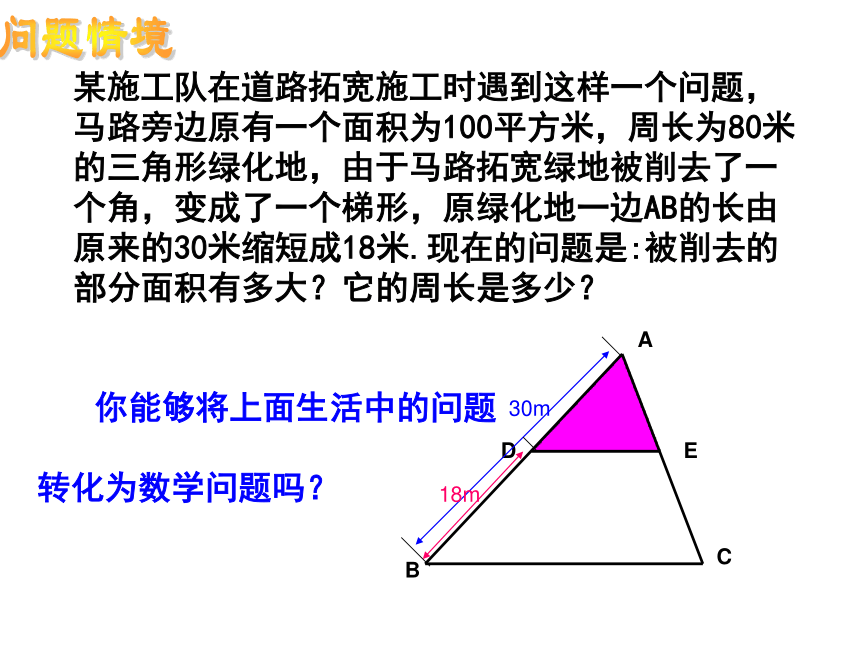
及其应用(1)某施工队在道路拓宽施工时遇到这样一个问题,马路旁边原有一个面积为100平方米,周长为80米的三角形绿化地,由于马路拓宽绿地被削去了一个角,变成了一个梯形,原绿化地一边AB的长由原来的30米缩短成18米.现在的问题是:被削去的部分面积有多大?它的周长是多少? 你能够将上面生活中的问题
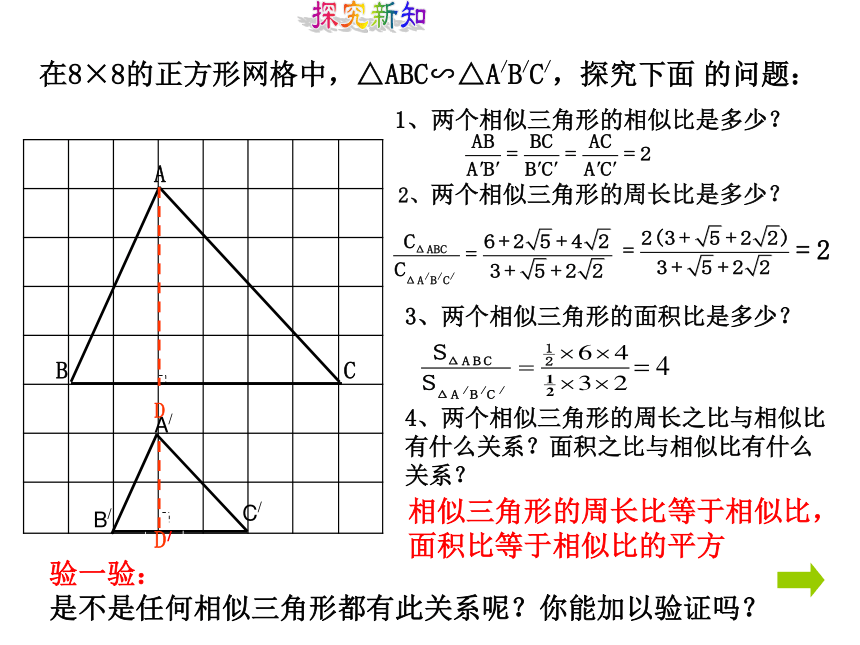
转化为数学问题吗?问题情境30m探究新知在8×8的正方形网格中,△ABC∽△A/B/C/,探究下面 的问题:1、两个相似三角形的相似比是多少?2、两个相似三角形的周长比是多少?3、两个相似三角形的面积比是多少?4、两个相似三角形的周长之比与相似比有什么关系?面积之比与相似比有什么关系?相似三角形的周长比等于相似比,
面积比等于相似比的平方验一验:
是不是任何相似三角形都有此关系呢?你能加以验证吗?探究新知相似三角形的周长比等于相似比;
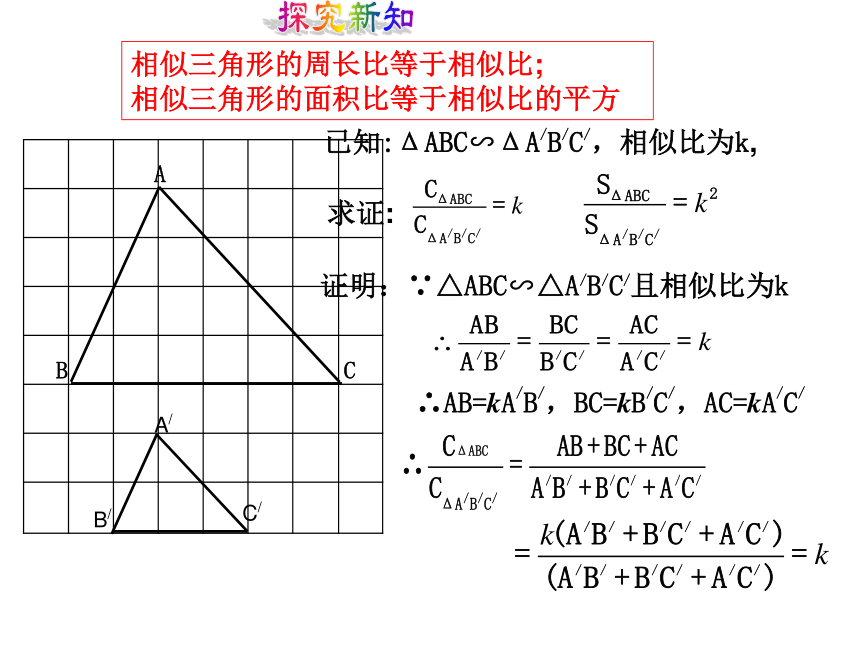
相似三角形的面积比等于相似比的平方
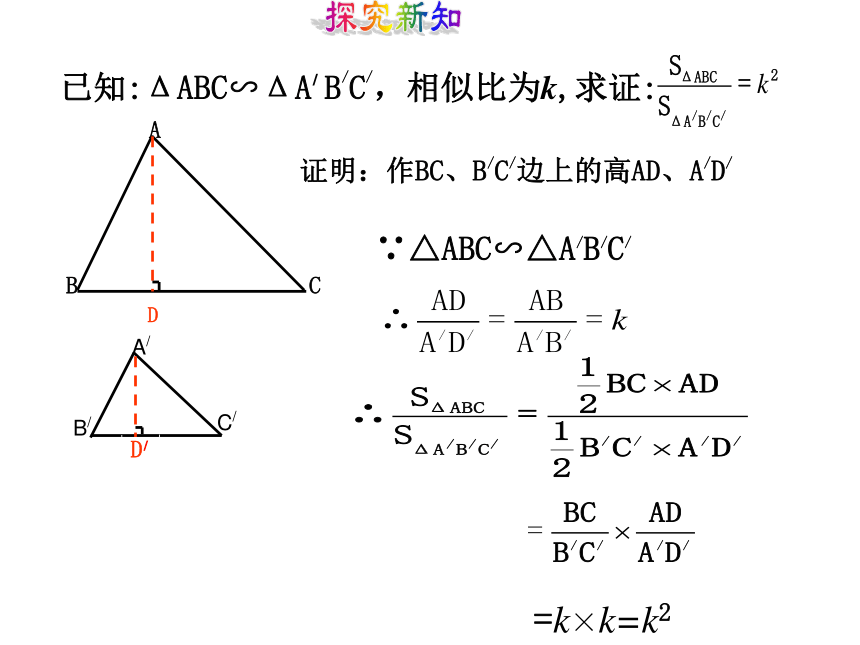
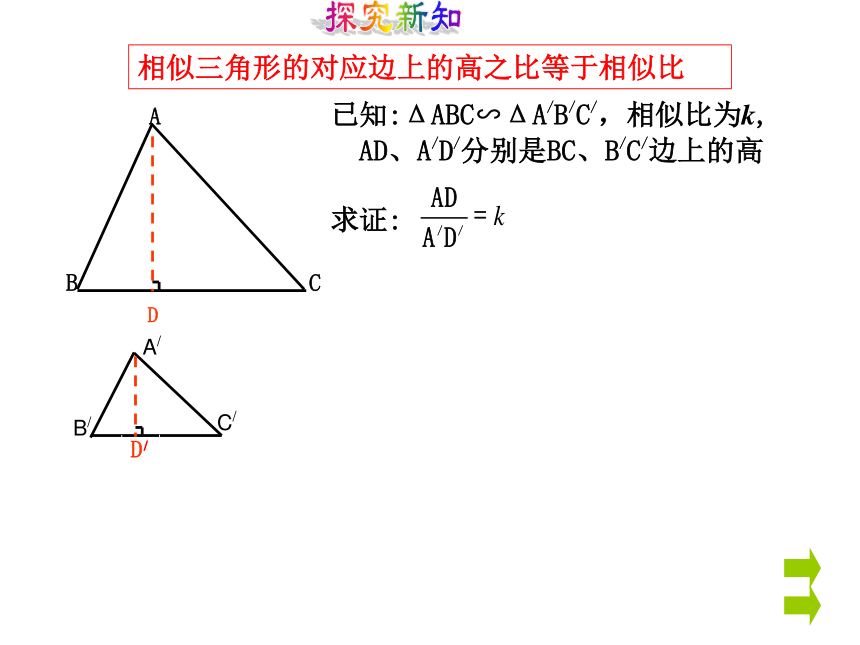
求证:已知:ΔABC∽ΔA/B/C/,相似比为k,证明:∵△ABC∽△A/B/C/且相似比为k∴AB=kA/B/,BC=kB/C/,AC=kA/C/探究新知证明:作BC、B/C/边上的高AD、A/D/∵△ABC∽△A/B/C/已知:ΔABC∽ΔA/ B/C/,相似比为k,求证:=k×k=k2探究新知相似三角形的对应边上的高之比等于相似比已知:ΔABC∽ΔA/B/C/,相似比为k,
AD、A/D/分别是BC、B/C/边上的高
求证:相似三角形对应边上的中线之比等于相似比
相似三角形对应边上的角平分线之比等于相似比
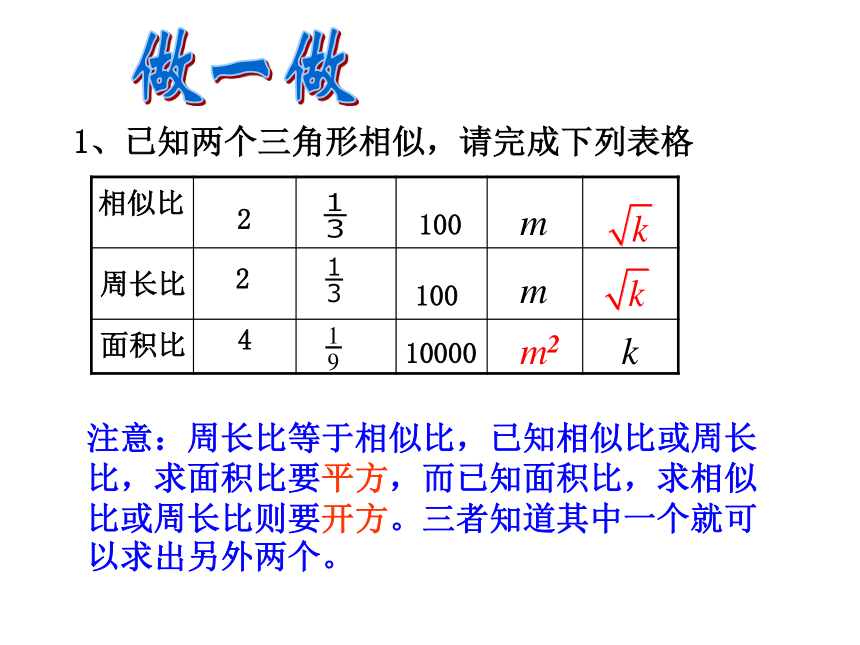
你能类比证明吗?1、已知两个三角形相似,请完成下列表格相似比周长比面积比24100100100002注意:周长比等于相似比,已知相似比或周长比,求面积比要平方,而已知面积比,求相似比或周长比则要开方。三者知道其中一个就可以求出另外两个。做一做mmm2k 在10倍的放大镜下看到的三角形与原三角形相比,
三角形的边长,周长,面积,角,哪些放大为10倍?答:三角形的边长,周长放大为10倍.三角形的面积放大为100倍.三角形的角大小不变.解:如图,已知DE//BC,AB=30m,BD=18m,
ΔABC的周长为80m,面积为100m2,
求ΔADE的周长和面积问题解决30m例:如图,是某市部分街道图,比例尺为1:10 000;请估计三条道路围成的三角形地块ABC的实际周长和面积。其中测得:AB=3.4cm, BC=3.8cm,AC=2.5cm,高AD=2.2cmC解:△ABC的周长=3.4+3.8+2.5=9.7cm∴三角形地块的实际周长为9.7×104cm,即970m∵S△ABC=3.8×2.2÷2=4.18(cm2)∴三角形地块的实际面积为4.18×108cm2,即41800m2答:估计三角形地块的周长为970cm,实际面积为41800m2。AB知识运用3.42.23.82.5如图,E、F分别是AB、AC上的点,EF∥BC,AE:AB=1:3(1)若BC=9cm,EF=___________(2)△AEF与△ABC的周长之比
=_________(3)△AEF与△ABC的面积之比
=_________
变1:当∠AFE=∠B,AF=2,AB=5时,你能得到哪些结论?若AD⊥BC于点D,AG⊥EF于点G,求AD:AG的值.变2:若EF∥BC,AE:EB=1:2,AD⊥BC于点D,交EF于点H,
AD=6cm,求AH的长.H3cm1:31:95:22cm知识运用25变3:
如图,已知△ABC,EF∥BC,与AB、AC分别交与点E、F,把△ABC划分成两部分(三角形与四边形)的面积之比为1:1,则AE:AB=?如果要使划分成的两部分的面积之比为1:2,则AE:AB=?如果要使划分成的两部分的面积之比为1:n,
则AE:AB=?1:1:1:知识运用30cm18cm变4:如图,已知EF//BC,AC=30cm,FC=18cm,ΔABC的周长为80cm,面积为100cm2,求ΔAEF的周长和面积过F作FP//AB交BC于P,其他条件
不变,则ΔFPC的面积等于多少?知识运用1、相似三角形的性质:课堂回顾这些知识你掌握了吗?3、运用相似三角形的性质解决简单的几何问题相似三角形的对应周长之比=相似比对应高之比=相似比对应面积之比=相似比的平方2、相似比、周长比、面积比中知道其中一个可以求
另两个量作业布置一、作业:
数学作业本(2)P25-26页二、课后思考:
1、证明相似三角形的对应边上的中线、角平分线之比等于
相似比。2、如图,△ABC中,EF∥BC,PF∥AB,若设SΔABC=S,
SΔAEF=S1,SΔFCP=S2.请猜想:S与S1、S2之间存在怎样的
关系?你能加以验证吗?EF 3、如图,△ABC中,EF∥GH∥BC,
AE=EG=GB,△AEF、四边形
EFHG、四边形GHCB的面积
依次记为S1、S2、S3。
则 S1:S2:S3=?如果延长AB、AC,使EF∥GH∥BC∥JK,AE=EG=GB=JK,四边形BCKJ的面积为S4,则S1:S2:S3:S4=?S4其余条件不变,AE:EG:GB=1:2:3,则S1:S2:S3=?挑战自我 如图,△ABC是一块锐角三角形余料,边BC=120毫米,高AD=80毫米,要把它加工成正方形零件,使正方形的一边在BC上,其余两个顶点分别在AB、AC上,这个正方形零件的边长是多少?NMQPEDCBA解:设正方形PQMN是符合要求的△ABC的高AD与PN相交于点E。设正方形PQMN的边长为x毫米。
因为PN∥BC,所以△APN∽ △ABC
所以在Rt△ ABC中,∠C=90。,AC=4,BC=3,(3)如图3,三角形内有并排的三个相等的正方形,它们组成的矩形内接于△ ABC,求正方形的边长。(2)如图2,三角形内有并排的两个相等的正方形,它们组成的矩形内接于△ ABC,求正方形的边长(1)如图1,四边形DEFG为△ ABC的内接正方形,求正方形的边长。
课外拓展(4)如图4,三角形内有并排的个正方形,它们组成的矩形内节于△ ABC,请写出正方形的边长。探究新知证明:∵△ABC∽△A/B/C/∴∠B=∠B/∵AD、A/D/分别是BC、B/C/边上的高∴∠ADB=∠A/D/B/=900∴△ABD∽△A/B/D/相似三角形的对应边上的高之比等于相似比已知:ΔABC∽ΔA/B/C/,相似比为k,
AD、A/D/分别是BC、B/C/边上的高,
求证:探究新知证明:∵△ABC∽△A/B/C/∴∠C=∠C/∵AD、A/D/分别是BC、B/C/边上的高相似三角形的对应边上的高之比等于相似比∴∠ADC=∠A/D/C/=900∴△ACD∽△A/C/D/已知:ΔABC∽ΔA/B/C/,相似比为k,
AD、A/D/分别是BC、B/C/边上的高,
求证:
及其应用(1)某施工队在道路拓宽施工时遇到这样一个问题,马路旁边原有一个面积为100平方米,周长为80米的三角形绿化地,由于马路拓宽绿地被削去了一个角,变成了一个梯形,原绿化地一边AB的长由原来的30米缩短成18米.现在的问题是:被削去的部分面积有多大?它的周长是多少? 你能够将上面生活中的问题
转化为数学问题吗?问题情境30m探究新知在8×8的正方形网格中,△ABC∽△A/B/C/,探究下面 的问题:1、两个相似三角形的相似比是多少?2、两个相似三角形的周长比是多少?3、两个相似三角形的面积比是多少?4、两个相似三角形的周长之比与相似比有什么关系?面积之比与相似比有什么关系?相似三角形的周长比等于相似比,
面积比等于相似比的平方验一验:
是不是任何相似三角形都有此关系呢?你能加以验证吗?探究新知相似三角形的周长比等于相似比;
相似三角形的面积比等于相似比的平方
求证:已知:ΔABC∽ΔA/B/C/,相似比为k,证明:∵△ABC∽△A/B/C/且相似比为k∴AB=kA/B/,BC=kB/C/,AC=kA/C/探究新知证明:作BC、B/C/边上的高AD、A/D/∵△ABC∽△A/B/C/已知:ΔABC∽ΔA/ B/C/,相似比为k,求证:=k×k=k2探究新知相似三角形的对应边上的高之比等于相似比已知:ΔABC∽ΔA/B/C/,相似比为k,
AD、A/D/分别是BC、B/C/边上的高
求证:相似三角形对应边上的中线之比等于相似比
相似三角形对应边上的角平分线之比等于相似比
你能类比证明吗?1、已知两个三角形相似,请完成下列表格相似比周长比面积比24100100100002注意:周长比等于相似比,已知相似比或周长比,求面积比要平方,而已知面积比,求相似比或周长比则要开方。三者知道其中一个就可以求出另外两个。做一做mmm2k 在10倍的放大镜下看到的三角形与原三角形相比,
三角形的边长,周长,面积,角,哪些放大为10倍?答:三角形的边长,周长放大为10倍.三角形的面积放大为100倍.三角形的角大小不变.解:如图,已知DE//BC,AB=30m,BD=18m,
ΔABC的周长为80m,面积为100m2,
求ΔADE的周长和面积问题解决30m例:如图,是某市部分街道图,比例尺为1:10 000;请估计三条道路围成的三角形地块ABC的实际周长和面积。其中测得:AB=3.4cm, BC=3.8cm,AC=2.5cm,高AD=2.2cmC解:△ABC的周长=3.4+3.8+2.5=9.7cm∴三角形地块的实际周长为9.7×104cm,即970m∵S△ABC=3.8×2.2÷2=4.18(cm2)∴三角形地块的实际面积为4.18×108cm2,即41800m2答:估计三角形地块的周长为970cm,实际面积为41800m2。AB知识运用3.42.23.82.5如图,E、F分别是AB、AC上的点,EF∥BC,AE:AB=1:3(1)若BC=9cm,EF=___________(2)△AEF与△ABC的周长之比
=_________(3)△AEF与△ABC的面积之比
=_________
变1:当∠AFE=∠B,AF=2,AB=5时,你能得到哪些结论?若AD⊥BC于点D,AG⊥EF于点G,求AD:AG的值.变2:若EF∥BC,AE:EB=1:2,AD⊥BC于点D,交EF于点H,
AD=6cm,求AH的长.H3cm1:31:95:22cm知识运用25变3:
如图,已知△ABC,EF∥BC,与AB、AC分别交与点E、F,把△ABC划分成两部分(三角形与四边形)的面积之比为1:1,则AE:AB=?如果要使划分成的两部分的面积之比为1:2,则AE:AB=?如果要使划分成的两部分的面积之比为1:n,
则AE:AB=?1:1:1:知识运用30cm18cm变4:如图,已知EF//BC,AC=30cm,FC=18cm,ΔABC的周长为80cm,面积为100cm2,求ΔAEF的周长和面积过F作FP//AB交BC于P,其他条件
不变,则ΔFPC的面积等于多少?知识运用1、相似三角形的性质:课堂回顾这些知识你掌握了吗?3、运用相似三角形的性质解决简单的几何问题相似三角形的对应周长之比=相似比对应高之比=相似比对应面积之比=相似比的平方2、相似比、周长比、面积比中知道其中一个可以求
另两个量作业布置一、作业:
数学作业本(2)P25-26页二、课后思考:
1、证明相似三角形的对应边上的中线、角平分线之比等于
相似比。2、如图,△ABC中,EF∥BC,PF∥AB,若设SΔABC=S,
SΔAEF=S1,SΔFCP=S2.请猜想:S与S1、S2之间存在怎样的
关系?你能加以验证吗?EF 3、如图,△ABC中,EF∥GH∥BC,
AE=EG=GB,△AEF、四边形
EFHG、四边形GHCB的面积
依次记为S1、S2、S3。
则 S1:S2:S3=?如果延长AB、AC,使EF∥GH∥BC∥JK,AE=EG=GB=JK,四边形BCKJ的面积为S4,则S1:S2:S3:S4=?S4其余条件不变,AE:EG:GB=1:2:3,则S1:S2:S3=?挑战自我 如图,△ABC是一块锐角三角形余料,边BC=120毫米,高AD=80毫米,要把它加工成正方形零件,使正方形的一边在BC上,其余两个顶点分别在AB、AC上,这个正方形零件的边长是多少?NMQPEDCBA解:设正方形PQMN是符合要求的△ABC的高AD与PN相交于点E。设正方形PQMN的边长为x毫米。
因为PN∥BC,所以△APN∽ △ABC
所以在Rt△ ABC中,∠C=90。,AC=4,BC=3,(3)如图3,三角形内有并排的三个相等的正方形,它们组成的矩形内接于△ ABC,求正方形的边长。(2)如图2,三角形内有并排的两个相等的正方形,它们组成的矩形内接于△ ABC,求正方形的边长(1)如图1,四边形DEFG为△ ABC的内接正方形,求正方形的边长。
课外拓展(4)如图4,三角形内有并排的个正方形,它们组成的矩形内节于△ ABC,请写出正方形的边长。探究新知证明:∵△ABC∽△A/B/C/∴∠B=∠B/∵AD、A/D/分别是BC、B/C/边上的高∴∠ADB=∠A/D/B/=900∴△ABD∽△A/B/D/相似三角形的对应边上的高之比等于相似比已知:ΔABC∽ΔA/B/C/,相似比为k,
AD、A/D/分别是BC、B/C/边上的高,
求证:探究新知证明:∵△ABC∽△A/B/C/∴∠C=∠C/∵AD、A/D/分别是BC、B/C/边上的高相似三角形的对应边上的高之比等于相似比∴∠ADC=∠A/D/C/=900∴△ACD∽△A/C/D/已知:ΔABC∽ΔA/B/C/,相似比为k,
AD、A/D/分别是BC、B/C/边上的高,
求证:
同课章节目录
