1.3解直角三角形(3)
图片预览

文档简介
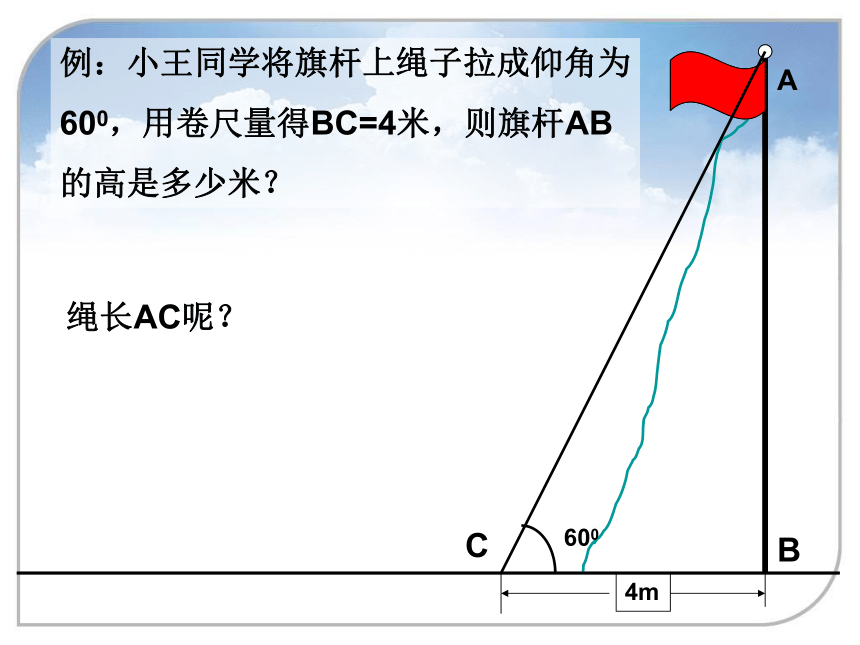
课件10张PPT。1.3 解直角三角形(3)例:小王同学将旗杆上绳子拉成仰角为
600,用卷尺量得BC=4米,则旗杆AB
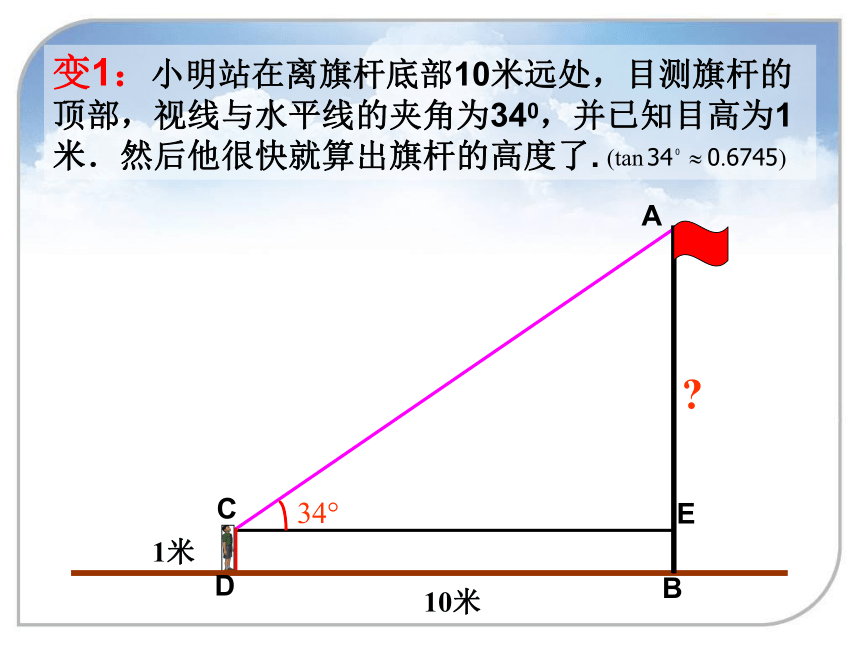
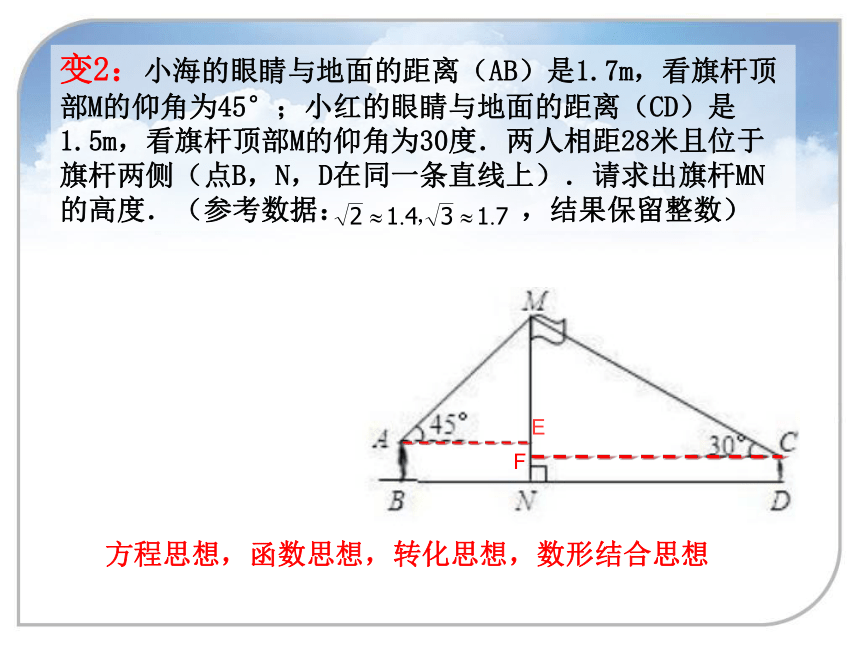
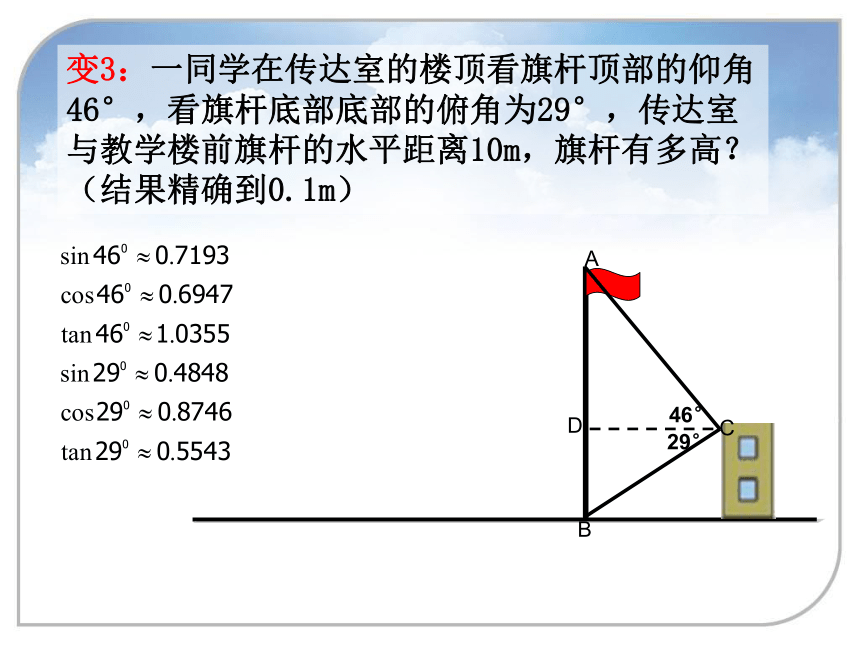
的高是多少米?C绳长AC呢?变1:小明站在离旗杆底部10米远处,目测旗杆的顶部,视线与水平线的夹角为340,并已知目高为1米.然后他很快就算出旗杆的高度了.1米10米?变2:小海的眼睛与地面的距离(AB)是1.7m,看旗杆顶部M的仰角为45°;小红的眼睛与地面的距离(CD)是1.5m,看旗杆顶部M的仰角为30度.两人相距28米且位于旗杆两侧(点B,N,D在同一条直线上).请求出旗杆MN的高度.(参考数据: ,结果保留整数) 方程思想,函数思想,转化思想,数形结合思想变3:一同学在传达室的楼顶看旗杆顶部的仰角46°,看旗杆底部底部的俯角为29°,传达室与教学楼前旗杆的水平距离10m,旗杆有多高?(结果精确到0.1m)变4:建筑物BC上有一旗杆AB,由距BC 50m的D处观察旗杆顶部A的仰角54°,观察底部B的仰角为45°,求旗杆的高度.变5:若小王同学分别在点C、点D处将旗杆上绳子分别拉成仰角为450、300,量出CD=10米,你能求出旗杆AB的长吗?A图1为已建设封顶的16层楼房和其塔吊图,图2为其
示意图,吊臂AB与地面EH平行,测得A点到楼顶D点
的距离为5m,每层楼高3.5m,AE、BF、CH都垂直于地
面,EF=16m,求塔吊的高CH的长.直角三角勾股弦
没有直角把线添
生活问题需建模
数学思想记心间Thank You !课件10张PPT。1.3 解直角三角形(3)例:小王同学将旗杆上绳子拉成仰角为
600,用卷尺量得BC=4米,则旗杆AB
的高是多少米?C绳长AC呢?变1:小明站在离旗杆底部10米远处,目测旗杆的顶部,视线与水平线的夹角为340,并已知目高为1米.然后他很快就算出旗杆的高度了.1米10米?变2:小海的眼睛与地面的距离(AB)是1.7m,看旗杆顶部M的仰角为45°;小红的眼睛与地面的距离(CD)是1.5m,看旗杆顶部M的仰角为30度.两人相距28米且位于旗杆两侧(点B,N,D在同一条直线上).请求出旗杆MN的高度.(参考数据: ,结果保留整数) 方程思想,函数思想,转化思想,数形结合思想变3:一同学在传达室的楼顶看旗杆顶部的仰角46°,看旗杆底部底部的俯角为29°,传达室与教学楼前旗杆的水平距离10m,旗杆有多高?(结果精确到0.1m)变4:建筑物BC上有一旗杆AB,由距BC 50m的D处观察旗杆顶部A的仰角54°,观察底部B的仰角为45°,求旗杆的高度.变5:若小王同学分别在点C、点D处将旗杆上绳子分别拉成仰角为450、300,量出CD=10米,你能求出旗杆AB的长吗?A图1为已建设封顶的16层楼房和其塔吊图,图2为其
示意图,吊臂AB与地面EH平行,测得A点到楼顶D点
的距离为5m,每层楼高3.5m,AE、BF、CH都垂直于地
面,EF=16m,求塔吊的高CH的长.直角三角勾股弦
没有直角把线添
生活问题需建模
数学思想记心间Thank You !
600,用卷尺量得BC=4米,则旗杆AB
的高是多少米?C绳长AC呢?变1:小明站在离旗杆底部10米远处,目测旗杆的顶部,视线与水平线的夹角为340,并已知目高为1米.然后他很快就算出旗杆的高度了.1米10米?变2:小海的眼睛与地面的距离(AB)是1.7m,看旗杆顶部M的仰角为45°;小红的眼睛与地面的距离(CD)是1.5m,看旗杆顶部M的仰角为30度.两人相距28米且位于旗杆两侧(点B,N,D在同一条直线上).请求出旗杆MN的高度.(参考数据: ,结果保留整数) 方程思想,函数思想,转化思想,数形结合思想变3:一同学在传达室的楼顶看旗杆顶部的仰角46°,看旗杆底部底部的俯角为29°,传达室与教学楼前旗杆的水平距离10m,旗杆有多高?(结果精确到0.1m)变4:建筑物BC上有一旗杆AB,由距BC 50m的D处观察旗杆顶部A的仰角54°,观察底部B的仰角为45°,求旗杆的高度.变5:若小王同学分别在点C、点D处将旗杆上绳子分别拉成仰角为450、300,量出CD=10米,你能求出旗杆AB的长吗?A图1为已建设封顶的16层楼房和其塔吊图,图2为其
示意图,吊臂AB与地面EH平行,测得A点到楼顶D点
的距离为5m,每层楼高3.5m,AE、BF、CH都垂直于地
面,EF=16m,求塔吊的高CH的长.直角三角勾股弦
没有直角把线添
生活问题需建模
数学思想记心间Thank You !课件10张PPT。1.3 解直角三角形(3)例:小王同学将旗杆上绳子拉成仰角为
600,用卷尺量得BC=4米,则旗杆AB
的高是多少米?C绳长AC呢?变1:小明站在离旗杆底部10米远处,目测旗杆的顶部,视线与水平线的夹角为340,并已知目高为1米.然后他很快就算出旗杆的高度了.1米10米?变2:小海的眼睛与地面的距离(AB)是1.7m,看旗杆顶部M的仰角为45°;小红的眼睛与地面的距离(CD)是1.5m,看旗杆顶部M的仰角为30度.两人相距28米且位于旗杆两侧(点B,N,D在同一条直线上).请求出旗杆MN的高度.(参考数据: ,结果保留整数) 方程思想,函数思想,转化思想,数形结合思想变3:一同学在传达室的楼顶看旗杆顶部的仰角46°,看旗杆底部底部的俯角为29°,传达室与教学楼前旗杆的水平距离10m,旗杆有多高?(结果精确到0.1m)变4:建筑物BC上有一旗杆AB,由距BC 50m的D处观察旗杆顶部A的仰角54°,观察底部B的仰角为45°,求旗杆的高度.变5:若小王同学分别在点C、点D处将旗杆上绳子分别拉成仰角为450、300,量出CD=10米,你能求出旗杆AB的长吗?A图1为已建设封顶的16层楼房和其塔吊图,图2为其
示意图,吊臂AB与地面EH平行,测得A点到楼顶D点
的距离为5m,每层楼高3.5m,AE、BF、CH都垂直于地
面,EF=16m,求塔吊的高CH的长.直角三角勾股弦
没有直角把线添
生活问题需建模
数学思想记心间Thank You !
