种群数量的变化

(共30张PPT)
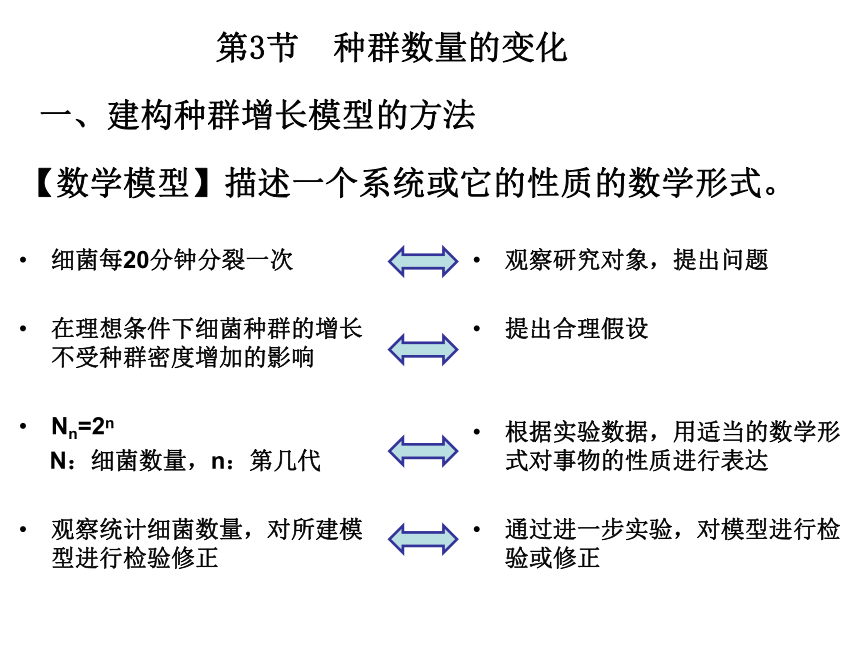
观察研究对象，提出问题
提出合理假设
根据实验数据，用适当的数学形式对事物的性质进行表达
通过进一步实验，对模型进行检验或修正
第3节　种群数量的变化
一、建构种群增长模型的方法
细菌每20分钟分裂一次
在理想条件下细菌种群的增长不受种群密度增加的影响
Nn=2n
　 N：细菌数量，n：第几代
观察统计细菌数量，对所建模型进行检验修正
【数学模型】描述一个系统或它的性质的数学形式。
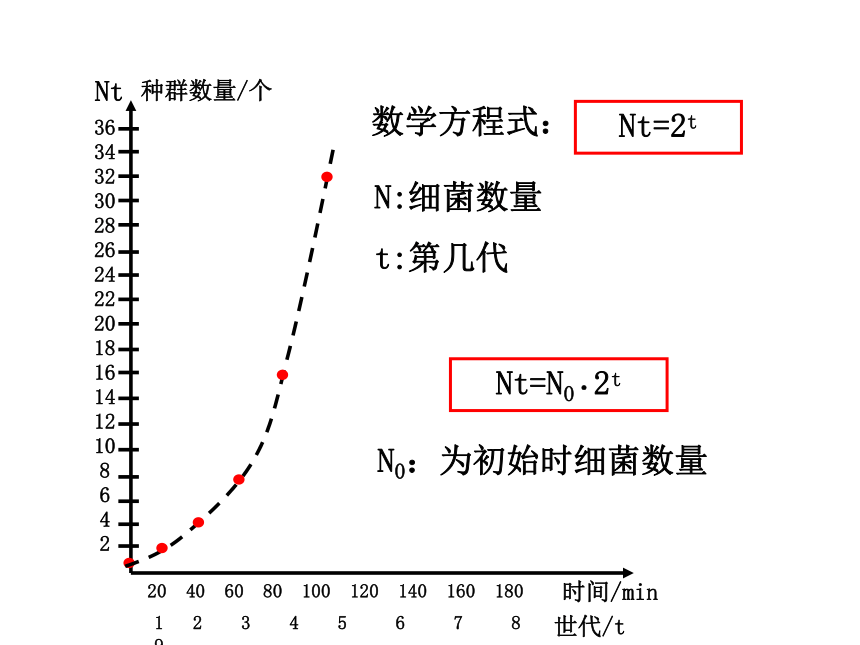
　　例1　在营养和生存空间无限的条件下，某种细菌每20min通过分裂繁殖一代，现设细菌的分裂是同步的，计算一个细菌产生的后代在不同时间、世代的数量，填表并画出种群的增长曲线。
时间(min) 20 40 60 80 100 120 140 160 180
世代
t 1 2 3 4 5 6 7 8 9
细菌数量
Nt 21 22 23 24 25 26 27 28 29
36
34
32
30
28
26
24
22
20
18
16
14
12
10
8
6
4
2
时间/min
种群数量/个
20　40　60　80　100　120　140　160　180　
Nt
Nt=2t
1　 2　 3　 4　 5　 6　 7　 8　 9
世代/t　
N:细菌数量
t:第几代
数学方程式：
Nt=N0·2t
N0：为初始时细菌数量
Nt = N0·λt =1×2t
N0：种群的起始数量
Nt：第t世代该种群的数量
t： 世代数
分析：在理想条件下，细菌种群的增长不受种群密度增加的影响，种群的世代净繁殖率（某世代为上一世代的倍数) λ将世代保持不变：
λ=1+r＝1＋（B－D）
r：种群增长率（r=B-D)
B：种群出生率
D：种群死亡率
时间
种群数量
Nt = N0·λt
当λ＞1时：
当λ＝1时：
时间
种群数量
当1＞λ＞0时：
时间
种群数量
当λ＝0时：
时间
种群数量
雌体未繁殖
λ＝0
种群在下一代灭亡
——在食物、空间充裕，气候适宜，无敌害的理想条件下，种群世代不重叠，呈离散增长的种群数量模型。如：一年生植物和昆虫。
λ=1+r
=1+(B-D)
出生率(B)=死亡率(D)
r=0
λ=1
种群数量稳定
出生率(B)＞死亡率(D)
r>0
λ>1
种群数量不断上升
出生率(B)<死亡率(D)
r<0
0<λ<1
种群数量不断下降
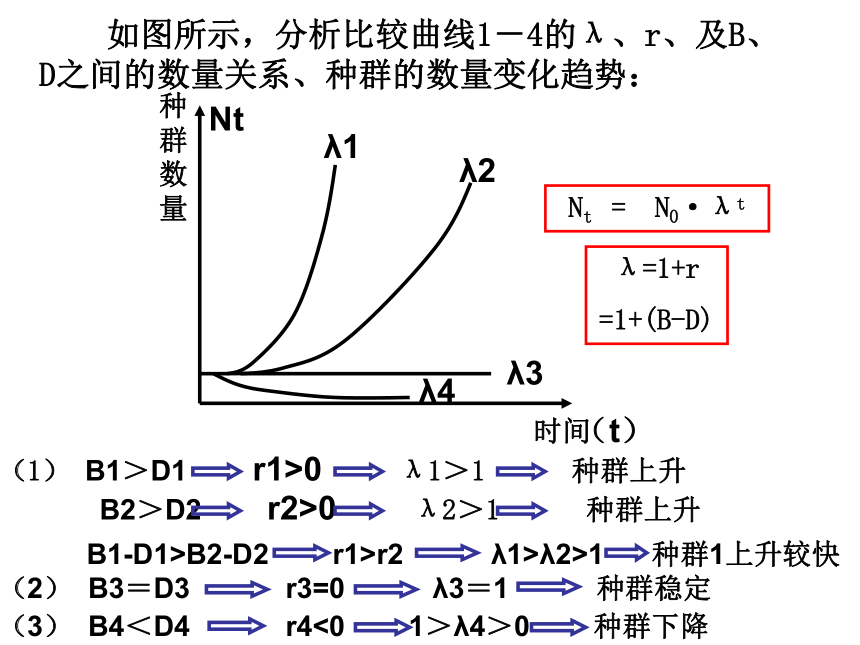
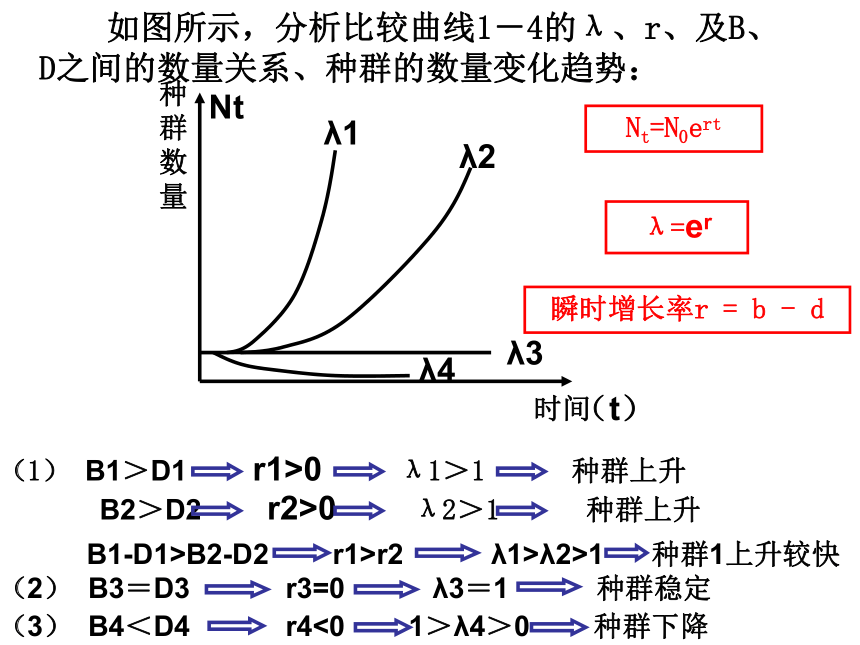
　　如图所示，分析比较曲线1－4的λ、r、及B、D之间的数量关系、种群的数量变化趋势：
Nt = N0·λt
种群数量
时间
λ1
λ2
λ3
λ4
Nt
（t）
λ=1+r
=1+(B-D)
（1） B1＞D1 　　r1>0 　　λ1＞1　　　种群上升
　　 B2＞D2 　　r2>0 　　λ2＞1　　　种群上升
B1-D1>B2-D2 r1>r2 λ1>λ2>1 种群1上升较快
（2） B3＝D3 r3=0 λ3＝1 种群稳定
（3） B4＜D4 r4<0 1＞λ4＞0 种群下降　
时间(t)
种群数量Nt
例2　1859年，24只野兔由英国带到澳大利亚，100年后，其后代竟达到6亿只以上，造成植被破坏，水土流失。引入黏液病毒才使野兔的数量得到控制。
分析：与上例比较，本例中野兔的世代是重叠的，种群的增长是连续的，在时间—种群数量坐标系中绘出曲线。
dN
dt
= (b-d) N = rN
　　在食物、空间充裕，气候适宜，无敌害的理想条件下，一个连续增长的种群其瞬时增长率与种群密度无关，将保持不变。
　　假定在很短时间dt内种群的瞬时出生率为b,瞬时死亡率为d，种群大小为N，则种群的瞬时增长率r = b - d，即：
积分式：Nt=N0ert
以种群大小Nt对时间t作图，得上图——“J”型曲线。
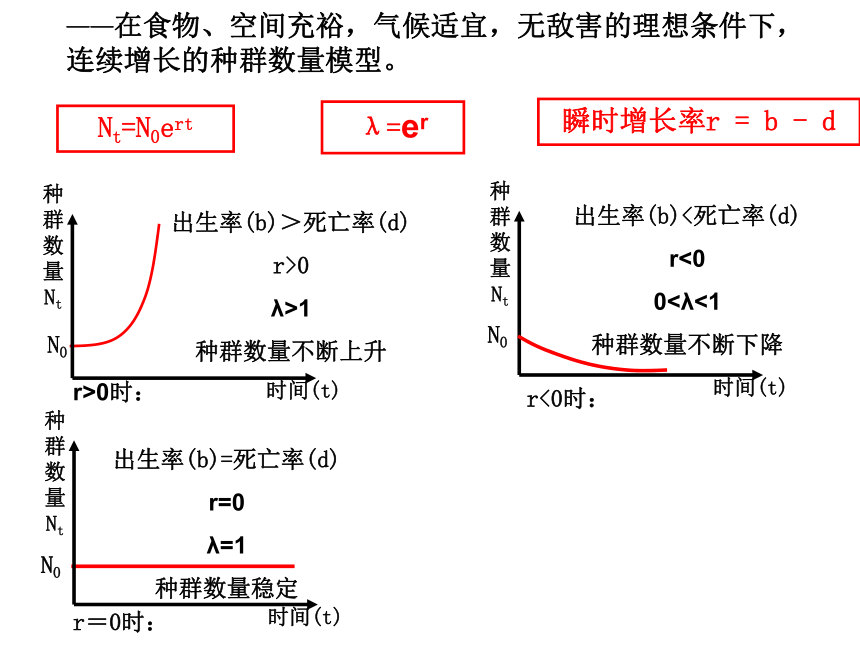
——在食物、空间充裕，气候适宜，无敌害的理想条件下，连续增长的种群数量模型。
出生率(b)=死亡率(d)
r=0
λ=1
种群数量稳定
Nt=N0ert
出生率(b)＞死亡率(d)
r>0
λ>1
种群数量不断上升
时间(t)
种群数量Nt
N0
r<0时：
出生率(b)<死亡率(d)
r<0
0<λ<1
种群数量不断下降
时间(t)
种群数量Nt
N0
r＝0时：
瞬时增长率r = b - d
λ=er
时间(t)
种群数量Nt
N0
r>0时：
　　如图所示，分析比较曲线1－4的λ、r、及B、D之间的数量关系、种群的数量变化趋势：
种群数量
时间
λ1
λ2
λ3
λ4
Nt
（t）
Nt=N0ert
瞬时增长率r = b - d
λ=er
（1） B1＞D1 　　r1>0 　　λ1＞1　　　种群上升
　　 B2＞D2 　　r2>0 　　λ2＞1　　　种群上升
B1-D1>B2-D2 r1>r2 λ1>λ2>1 种群1上升较快
（2） B3＝D3 r3=0 λ3＝1 种群稳定
（3） B4＜D4 r4<0 1＞λ4＞0 种群下降　
二、 “J ” 型增长的数学模型（P66）
【模型假设】
【建立模型】
Nt = N0·λt
时间(t)
种群数量Nt
N0
食物、空间条件充裕，气候适宜，无敌害等理想条件下，种群的数量每年以一定的倍数增长，第二年的数量是第一年的λ倍。
t年后种群数量：
λ=1+r
=1+(B-D)
【分析】同数学方程式相比，曲线图表示的数学模型有什么局限性？
出生率(B)＞死亡率(D)
r>0
λ>1
种群数量不断上升
环境容纳量
减速期
开始期
加速期
转折点
饱和期
时间
种群数量
K
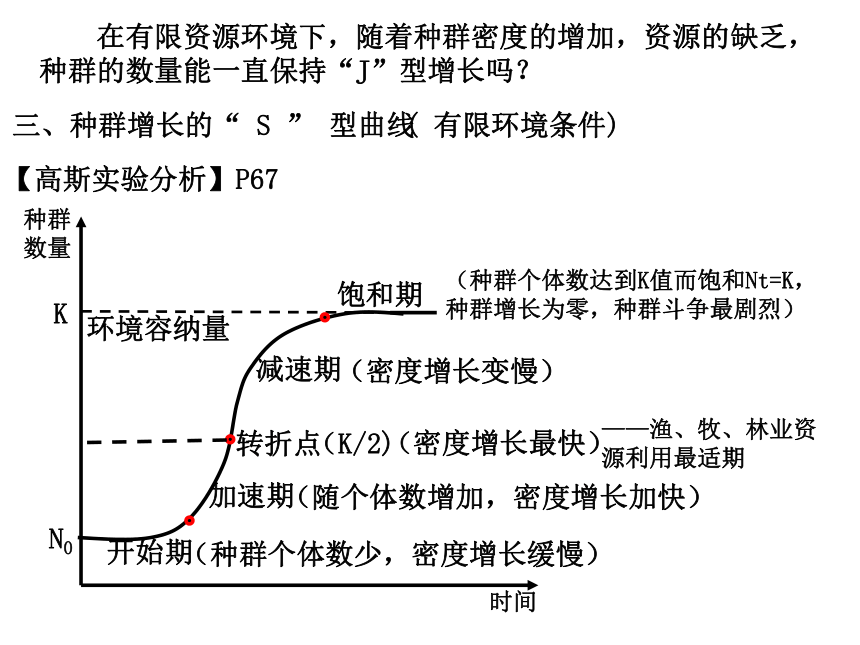
【高斯实验分析】P67
——渔、牧、林业资源利用最适期
N0
（K/2)
三、种群增长的“ S ” 型曲线
( 有限环境条件)
（种群个体数少，密度增长缓慢）
（随个体数增加，密度增长加快）
（密度增长最快）
（密度增长变慢）
（种群个体数达到K值而饱和Nt=K，种群增长为零，种群斗争最剧烈）
　　在有限资源环境下，随着种群密度的增加，资源的缺乏，种群的数量能一直保持“J”型增长吗？
　　在有限资源环境下，随着种群密度的增加，资源缺乏，种群的出生率降低、死亡率升高，将使种群增长率降低。
dN
dt
= r·N＝
r=rm·( 1-N /k )
时间
种群数量
K
环境容纳量
rm·( 1-N /k ) ·N
积分式：
Nt=K/(1+ea-rt)
式中a值取决于N0
rm:种群在理想条件下的瞬时增长率
r: 种群在有限条件下的瞬时增长率
每增加一个个体，就产生1/K的抑制影响：N/K为环境阻力
【 “S”型增长的数学模型】
以种群数量Nt对时间t作图，得下图“S”型曲线。
dN
dt
= r·N＝
rm·( 1-N /k ) ·N
当K＞N时，种群正增长
当K＜N时，种群负增长
当K＝N时，种群呈稳定平衡
r和K参数的意义：
　　r：物种潜在的增长能力（生殖潜能）
　　K：环境容纳量，在特定环境中种群密度可能的最大值。
0 N0 K/2 K N
最大持续产量
dN/dt
种群的增长量
种群数量
鱼类的最大捕获量
种群增长的“S”型曲线的另一种表现方式：
时间
种群数量
K
环境容纳量
【分析】下图为理想条件下和自然环境下的某生物种群数量变化曲线。图中的阴影部分的含义？
1、环境中影响种群增长的阻力：
2、数量表示通过生存斗争被淘汰的个体数量　
【分析】同一种群的K值是否固定不变？
大熊猫　　　　　　　食物、活动范围减少　　　K值下降
栖息地被破坏
1　珍稀野生动物的保护：大熊猫
建自然保护区，改善栖息环境，扩大其生存空间，提高K值
【应用】
【保护大熊猫的根本措施】
2、有害动物的控制：家鼠
断食、切断巢穴、养殖并释放天敌——降低K值
器械捕杀、药物捕杀
四、种群数量的波动和下降
【影响种群数量的因素】
食物、天敌、传染病、栖息空间、气候、人类活动
【分析】上述哪些因素的作用随着种群的密度的变化而改变？
种群数量Nt
时间t
K
Nt (种群数量)
1、密度制约因素
食物、天敌（捕食、寄生、竞争）、传染病、栖息空间、
【密度制约因素的反馈调节】
时间/年
种群数量
例1：草（食物）对旅鼠的反馈调节作用
例2：抑制物的分泌
蝌蚪在种群密度高时分泌毒素
桉树在种群密度高时自毒现象
例3：传染病、寄生物对种群密度大的种群影响更大
——①使种群数量相对稳定或有规则的波动。
　　②具反馈调节机制
【分析】密度制约因素对种群数量影响的特点？
（减少）
羊
狼
草
（增加）
（增加）
（－）
（减少）
种群数量Nt
时间t
K
羊Nt
食物（草）
天敌（狼）
密度制约因素
密度制约因素对种群数量的反馈调节
2、非密度制约因素
气候、人类活动（如使用杀虫剂）
【分析】非密度制约因素对种群数量影响的特点？
例：干旱导致蝗虫的大发生
　　人类使用杀虫剂导致某害虫种群数量骤减
①引起种群数量不规则变动
②作用本身没有反馈调节，对种群数量的影响多为猛烈的、灾难性的。
③其作用可被密度制约因素所调节。
五、研究种群数量变化规律及影响因素的意义
1、有害动物的防治
2、野生生物资源的保护和合理利用
3、濒危动植物种群的拯救和恢复
【探究】培养液中酵母菌种群数量的变化
1【问题】培养液中酵母菌的数量是怎样随时间变化的？
①在不同温度下酵母菌的数量随时间变化？
②在不同通气条件（通O2与通CO2）下酵母菌的数量随时间变化？
③在理想条件下酵母菌的数量随时间变化？
④在有限条件下酵母菌的数量随时间变化？
2【作出假设】
围绕具体问题，合理提出符合逻辑的假设
时间
种群数量
K1
K2
3【讨论探究思路】
①材料用具：菌种、无菌马铃薯培养液或肉汤培养液、试管、血球计数板（、滴管、恒温培养箱、充气泵、显微镜等。
②对酵母菌计数的方法——血球计数板直接计数法
微生物计数室
微生物计数室（ 16×25）
每小格长、宽都是0.05mm，深度为0.1mm，体积为：
0.05×0.05×0.1=0.00025mm3
整个计数室的的体积：
0.00025mm3×16×25＝0.1mm3
相当于1/10000mL
每mL菌数＝　　　　　　　　　×400×10000×稀释倍数
80个小方格的菌数
80
【操作步骤】
2　滴加已知稀释浓度的菌悬液
1　盖片
从一侧滴加，不要产生气泡
3　镜检计数：
静置数分钟，待全部细胞沉降到玻片表面，再镜检。
计数时数上不数下，数左不数右
稀释度以每小方格内有5－10个菌体为宜
调整细准焦螺旋，找到计数室内上、下全部菌体。
计数应重复3次，取平均值
从试管中吸取菌体培养液时，将试管轻震荡几次
计数次数 各中方格中的菌数 1mL菌液中总菌数 三次平均数
1 2 3 4 5
第1次
第2次
第3次
实验结果记录表
【分析】本实验是否需要设计对照组？如何设计？
4【制订计划】
5【实施计划】
计数结果 各中方格中的菌数 1mL菌液中总菌数 三次平均数
1 2 3 4 5
初始值 第1次 N0
第2次
第3次
第1天 N1
…
第7天 N7
6【分析结果，得出结论】
7【表达与交流】
8【进一步探究】
种群数量
时间
Nt
　（D）
1. 美国某岛上的环颈雉种群的增长大致符合“J”型曲线。已知1939年，该岛有250只环颈雉，1942年变为1250只，请估算该岛环颈雉的年增长的倍数为：
　A　0　　　 B　1.2 C 1.5 D 1.7
D
2.1986年，西双版纳热带雨林犀鸟的数量为2860只，1987年再次统计显示，在一年内共新生幼鸟235只，死亡犀鸟共计186只，求犀鸟种群的出生率、死亡率、种群的年增长率？
R=B－D=1.71%
B=235/2860=8.22%
D=186/2860=6.5%