二次函数复习

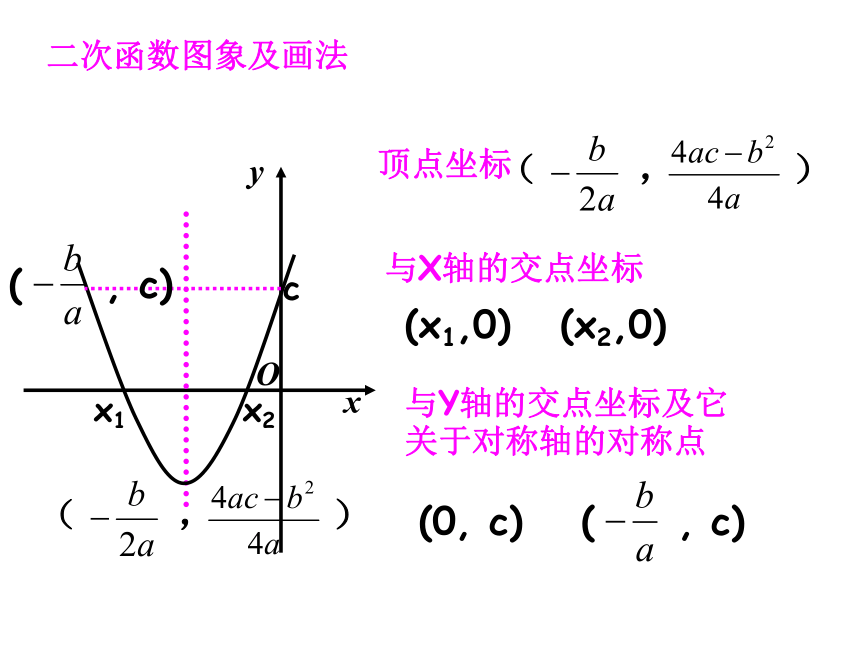
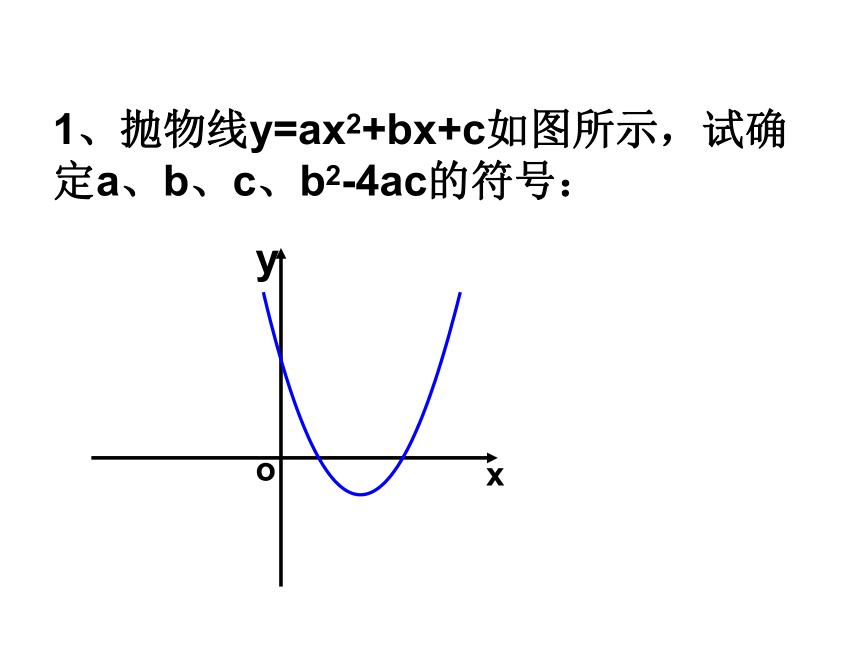
课件23张PPT。二次函数图象及画法顶点坐标与X轴的交点坐标与Y轴的交点坐标及它关于对称轴的对称点（ ， ）(x1,0) (x2,0)(0, c) ( , c) （ ， ）x1x2Oxyc( , c) 1、若抛物线y=ax2+3x-4与抛物线y=-2x2形状相同，则a= .2、二次函数y=x2+1的图象的顶点坐标是 .3、二次函数y=ax2+bx+c的图象与x轴的两个交点分别为A(1,0),B(-3,0)则它的对称轴是 .4、二次函数y=x2-2x+2 当x= 时，y的最小值为 .5、二次函数y=4x2+mx+1的图象顶点在x轴上，则m= ；若它的顶点在y轴上，则m= .±2(0,1)直线x=-111±40X=1、抛物线y=ax2+bx+c如图所示，则( )
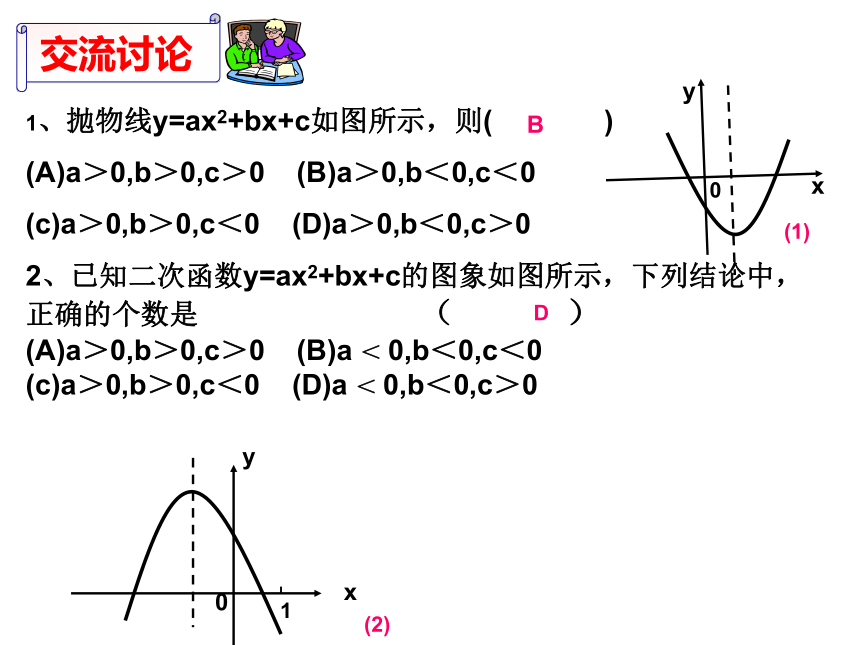
(A)a＞0,b＞0,c＞0 (B)a＞0,b＜0,c＜0
(c)a＞0,b＞0,c＜0 (D)a＞0,b＜0,c＞0
2、已知二次函数y=ax2+bx+c的图象如图所示，下列结论中，正确的个数是 （ ）
(A)a＞0,b＞0,c＞0 (B)a ＜ 0,b＜0,c＜0
(c)a＞0,b＞0,c＜0 (D)a ＜ 0,b＜0,c＞0
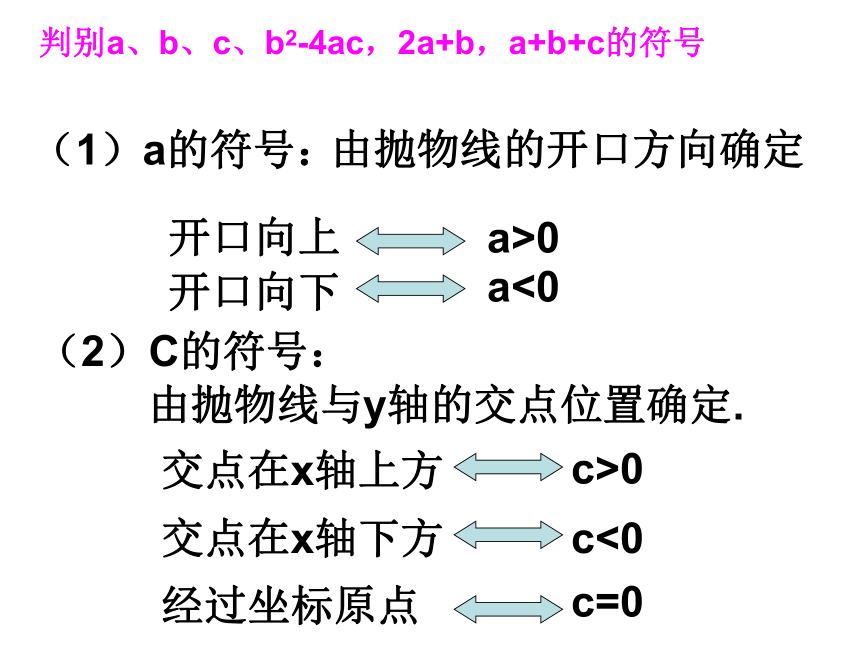
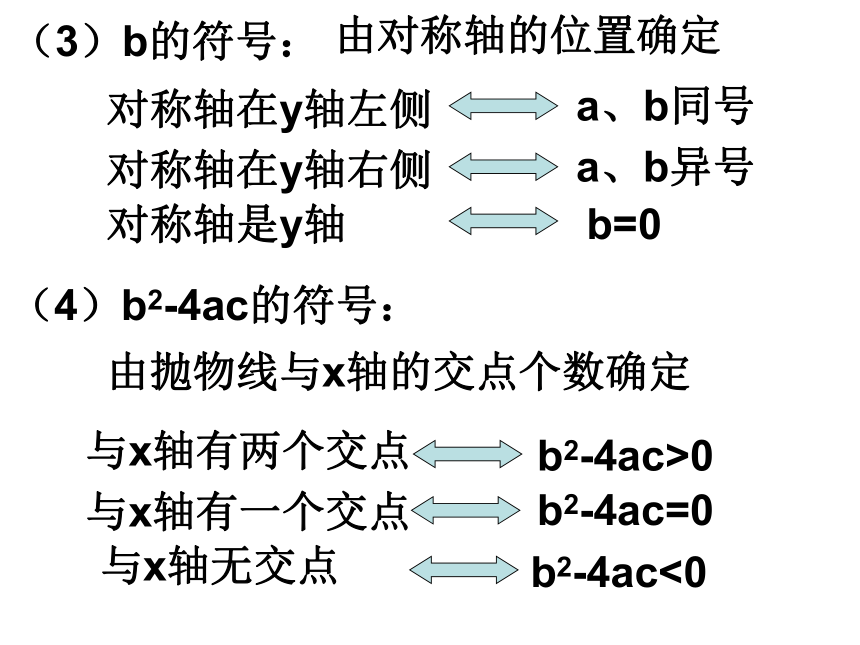
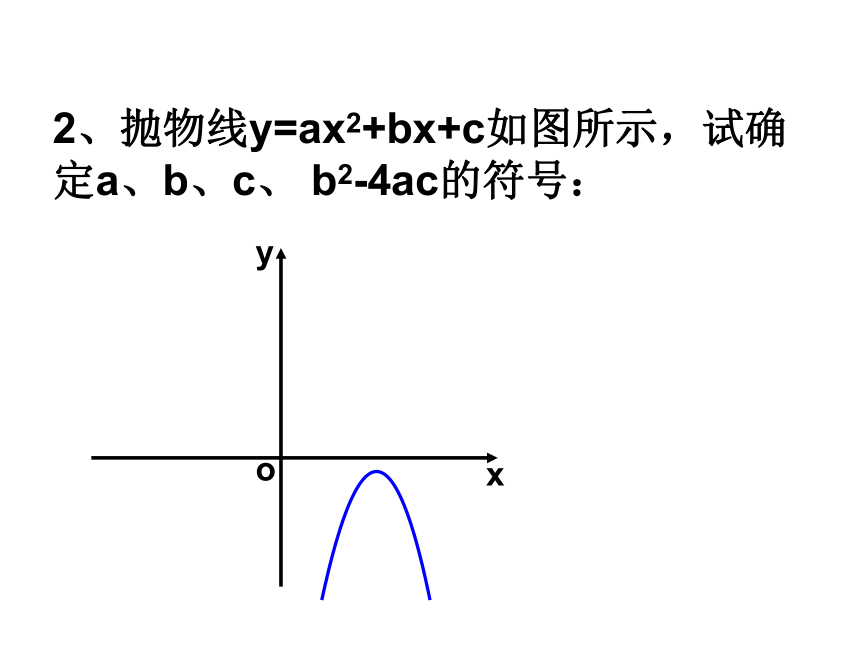
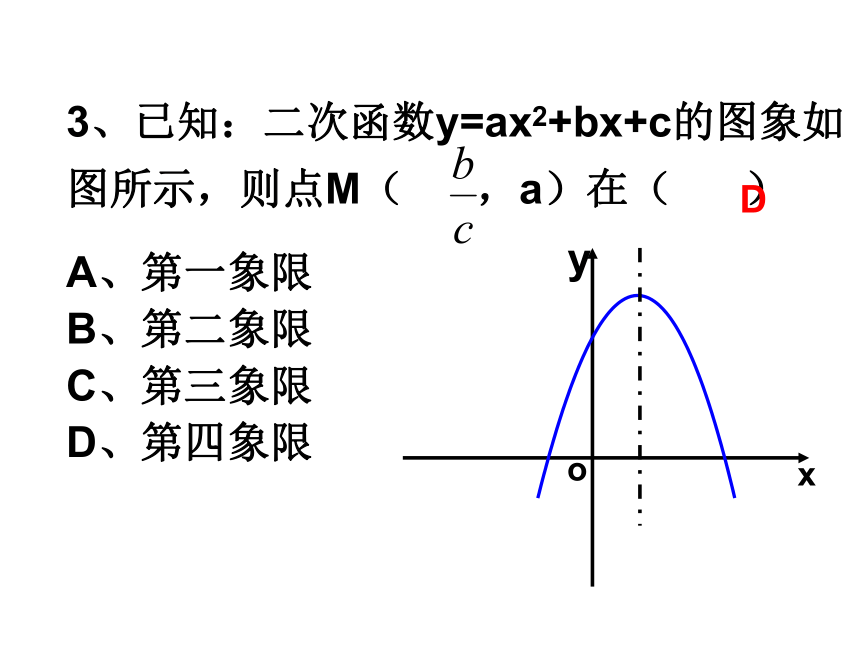
xyxy0(2)(1)B1D判别a、b、c、b2-4ac，2a+b，a+b+c的符号（1）a的符号：由抛物线的开口方向确定开口向上a>0开口向下a<0（2）C的符号：由抛物线与y轴的交点位置确定.交点在x轴上方c>0交点在x轴下方c<0经过坐标原点c=0（3）b的符号：由对称轴的位置确定对称轴在y轴左侧a、b同号对称轴在y轴右侧a、b异号对称轴是y轴b=0（4）b2-4ac的符号：由抛物线与x轴的交点个数确定与x轴有两个交点b2-4ac>0与x轴有一个交点b2-4ac=0与x轴无交点b2-4ac<0看方向 (上正、下负）看交点 (上正、下负)二次函数的图象看对称轴(左同、右异) 1、抛物线y=ax2+bx+c如图所示，试确定a、b、c、b2-4ac的符号：xyo2、抛物线y=ax2+bx+c如图所示，试确定a、b、c、 b2-4ac的符号：xyo3、已知：二次函数y=ax2+bx+c的图象如图所示，则点M（ ，a）在（ ）A、第一象限
B、第二象限
C、第三象限
D、第四象限 xoyD练一练：已知y=ax2+bx+c的图象如图所示,

a___0, b____0, c_____0, abc____0
b___2a, 2a-b_____0, 2a+b_______0
b2-4ac_____0
a+b+c_____0, a-b+c____0

4a-2b+c_____00-11-2＜＜＜＜＞＞＞＜＞＞＞已知二次函数
y=ax2+bx+c的图象如图所
示,下列结论①a+ b + c<0
②a – b + c>0 ③abc>0 ④
b=2a。其中正确的结论的
个数是（ ）
A 1个 B 2个 C 3个 D 4个mnD16、已知：一次函数y=ax+c与二次函数y=ax2+bx+c，它们在同一坐标系中的大致图象是图中的（ ）（A）（B）（C）（D）C开启 智慧
你说 我说1、函数y=ax2+bx+c的图象如图所示。X= 为该函数图象的对称轴，根据这个函数图象，你能得到关于该函数的哪些性质和结论？xyX=o-11-12、已知抛物线顶点坐标（m, k），通常设抛物线解析式为_______________3、已知抛物线与x 轴的两个交点(x1,0)、 (x2,0),通常设解析式为_____________1、已知抛物线上的三点，通常设解析式为________________y=ax2+bx+c(a≠0)y=a(x-m)2+k(a≠0)y=a(x-x1)(x-x2) (a≠0)三、求抛物线解析式常用的三种方法一般式顶点式交点式或两根式1、已知一个二次函数的图象经过点
（0，0），（1，﹣3），（2，﹣8）。求下列条件下的二次函数的解析式:作业3、已知二次函数的图象的对称轴是直线x=3,并且经过点(6,0),和(2,12)作业2、已知二次函数的图象的顶点坐标为
（－2，－3），且图象过点（－3，－2）。作业4、根据下列条件求y关于x的二次函数的解析式：1)图象过点（0，－2）、（1，2），且对称轴为直线2)图象经过（0，1）、（1，0）、（3，0）．3)当＝3时，y最小值＝－1，且图象过（0，7）．4)抛物线顶点坐标为（－1，－2），且过点（1，10）．5、 已知二次函数y=x2+bx+c的顶点坐标（1，-2），求b，c的值6、 已知二次函数y=x2+4x+c的顶点坐标在x轴上，求c的值7、 已知二次函数y=x2+4x+c的顶点坐标在直线y=2x+1上，求c的值8、 已知二次函数y=x2+4x+c有最小值为2，求c的值9、 已知二次函数y=-2x2+bx+c，当x=-2时函数有最大值为2，求b、c的值利用二次函数的图象求一元二次方程的近似解 2、根据下列表格的对应值：
判断方程ax2+bx+c=0（a≠0,a、b、c为常数）一个解的范围是　（　　　　）
Ａ、3＜x＜3.23 Ｂ、3.23＜x＜3.24
Ｃ、3.24＜x＜3.25 Ｄ、3.25＜x＜3.26一场篮球赛中，小悦跳起投篮，已知球出手时离地面高 米，与篮圈中心的水平距离为8米，当球出手后水平距离为4米时到达最大高度4米，设篮球运行的轨迹为抛物线，篮圈中心距离地面3米。3米8米4米4米实际运用之思维激活问此球能否投中？0如图，建立平面 直角坐标系，点（4，4）是图中这段抛物线的顶点，因此可设这段抛物线对应的函数为：(0≤x≤8)(0≤x≤8)∵篮圈中心距离地面3米∴此球不能投中。假设出手的角度和力度都不变,
则如何才能使此球命中? 跳得高一点向前平移一点实际运用之思维激活yx（4，4）（8，3）在出手角度和力度都不变的情况下,小悦的出手高度为多少时能将篮球投入篮圈?0 1 2 3 4 5 6 7 8 9