二次函数复习--二次函数中的面积问题

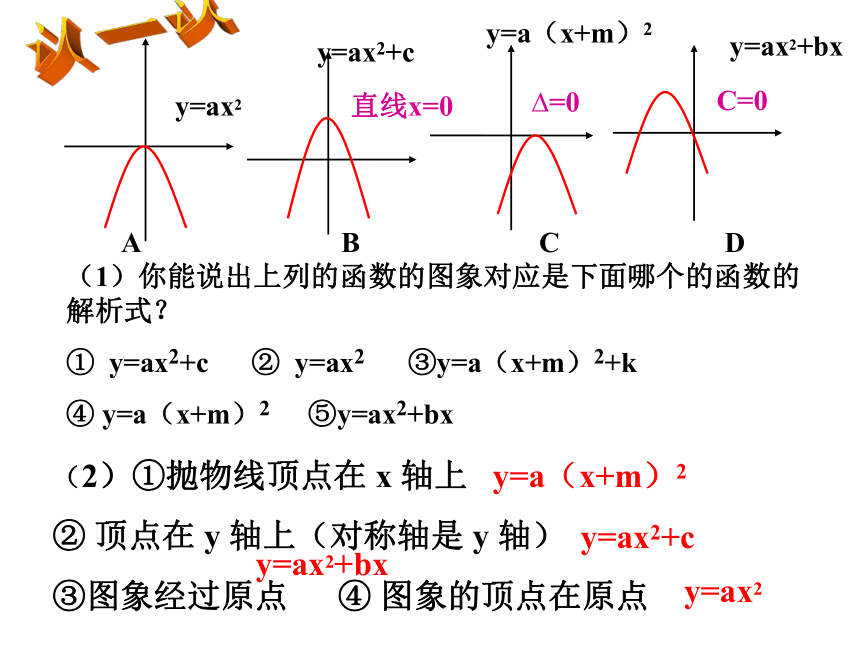
课件18张PPT。二次函数复习二次函数中的面积问题认一认（1）你能说出上列的函数的图象对应是下面哪个的函数的解析式？
① y=ax2+c ② y=ax2 ③y=a（x+m）2+k
④ y=a（x+m）2 ⑤y=ax2+bx A B C D（2）①抛物线顶点在 x 轴上
② 顶点在 y 轴上（对称轴是 y 轴）
③图象经过原点 ④ 图象的顶点在原点?=0C=0直线x=0y=ax2+cy=a（x+m）2y=ax2+bx
y=ax2y=a（x+m）2y=ax2+cy=ax2+bx
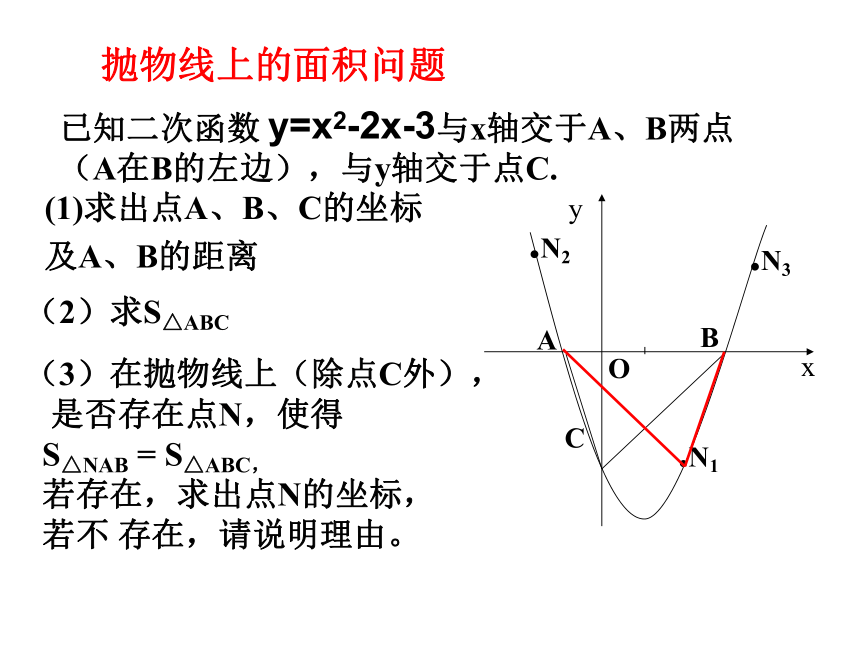
y=ax2 抛物线上的面积问题
已知二次函数 与x轴交于A、B两点（A在B的左边），与y轴交于点C.(1)求出点A、B、C的坐标
及A、B的距离（2）求S△ABC（3）在抛物线上（除点C外），
是否存在点N，使得
S△NAB = S△ABC，
若存在，求出点N的坐标，
若不 存在，请说明理由。.N1.N2.N3y=x2-2x-3 抛物线上的面积问题
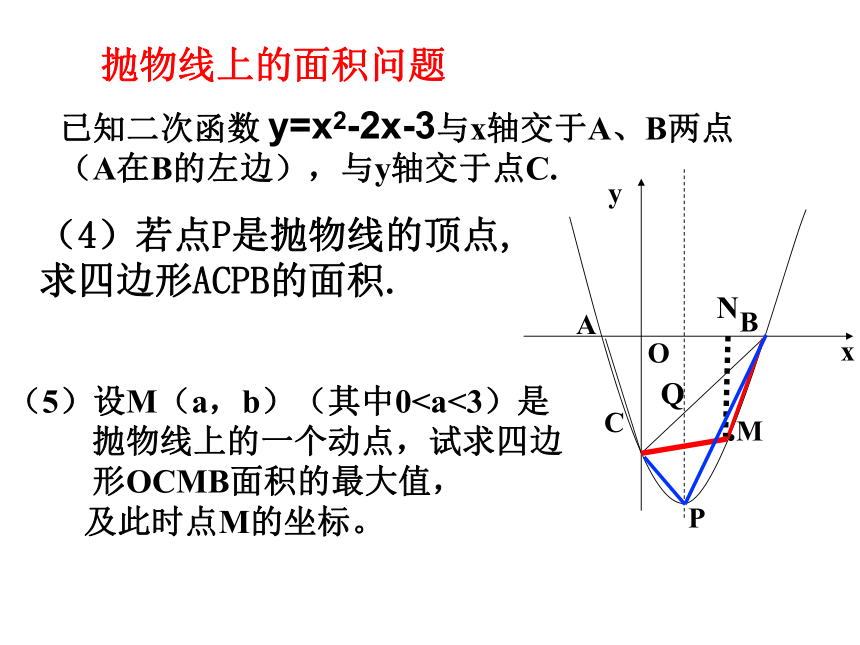
已知二次函数 与x轴交于A、B两点（A在B的左边），与y轴交于点C.（4）若点P是抛物线的顶点,
求四边形ACPB的面积.（5）设M（a，b）（其中0 抛物线上的一个动点，试求四边
形OCMB面积的最大值，
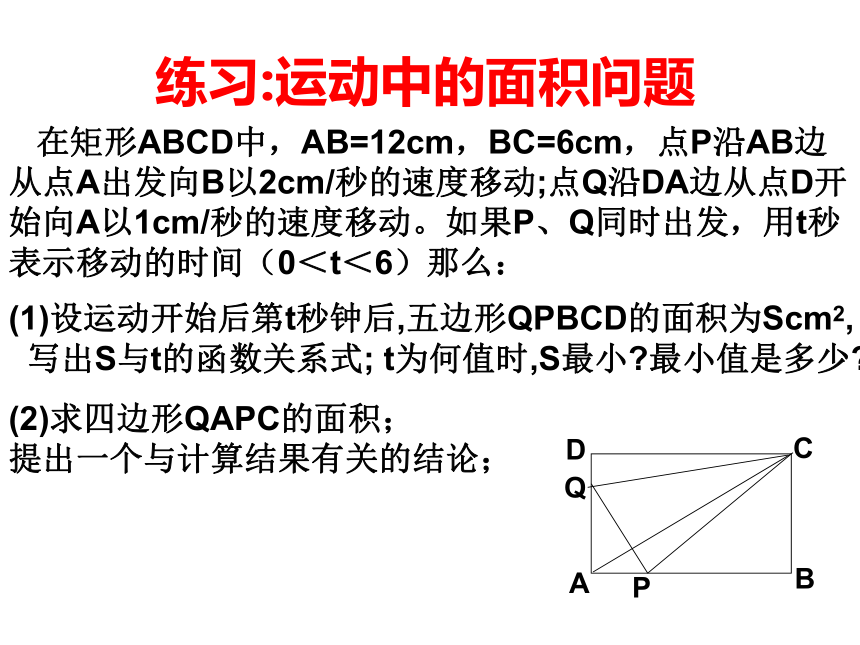
及此时点M的坐标。y=x2-2x-3.MNQH练习:运动中的面积问题 在矩形ABCD中，AB=12cm，BC=6cm，点P沿AB边从点A出发向B以2cm/秒的速度移动;点Q沿DA边从点D开始向A以1cm/秒的速度移动。如果P、Q同时出发，用t秒表示移动的时间（0＜t＜6）那么： QPADCB(1)设运动开始后第t秒钟后,五边形QPBCD的面积为Scm2,
写出S与t的函数关系式; t为何值时,S最小?最小值是多少?
(2)求四边形QAPC的面积；
提出一个与计算结果有关的结论；
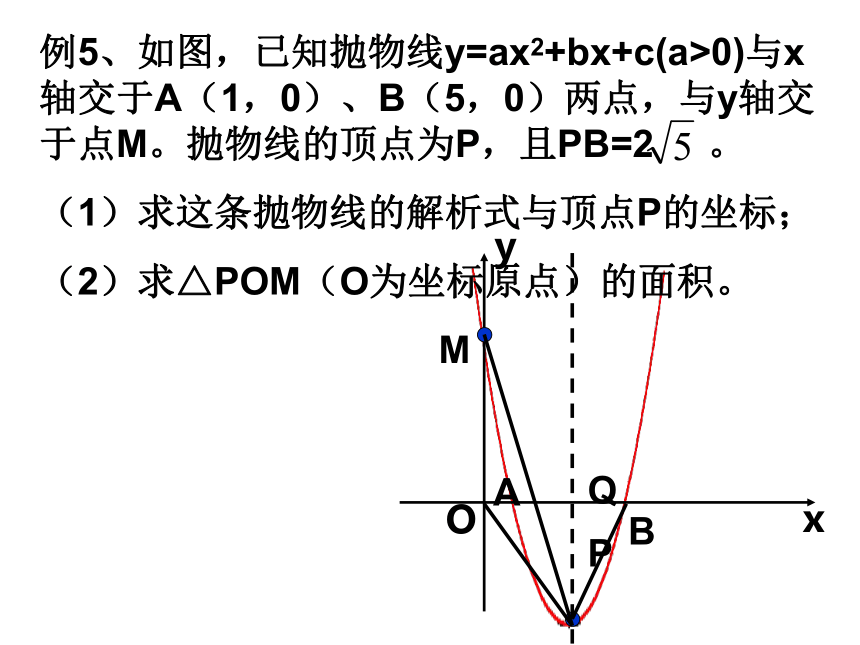
例5、如图，已知抛物线y=ax2+bx+c(a>0)与x轴交于A（1，0）、B（5，0）两点，与y轴交于点M。抛物线的顶点为P，且PB=2 。
（1）求这条抛物线的解析式与顶点P的坐标；
（2）求△POM（O为坐标原点）的面积。例3 已知二次函数的图象如图，
（1）求二次函数的解析式 ；
【解】（１） 由图象看出A（-1，0），B（2，0） C（O，-2）
设抛物线解析式为：y=a（x- 2）（ｘ＋１）Ｃ在抛物线上，∴ａ＝１
　　∴抛物线解析式为：ｙ＝ｘ２－ｘ－２
解（2）设过B（2，0） M（ ，－ ）的解析式为：ｙ＝ｋｘ＋ｂ
　　　　　　　则　ｋ＝　　　　　ｂ＝－３∴直线ＢＭ的解析式为：
　　
　　　ｙ＝　　ｘ－３　　　∵QＮ=t　　∴把ｙ＝ｔ代入直线
ＭＢ的解析式，
　　　　　得ｘ＝２－　ｔ
∴S＝　　×２×１＋　（２＋ｔ）（2－ t）　　　

即S＝- t2 ＋ t ＋3 其中 0＜t＜
（2）若点N为线段BM上的一点，过点N 作x轴的垂线，垂足为Q，当点N在线段BM上运动时（不与点B、点M重合）设NQ的长为t，四边形NQAC的面积为S，求S与ｔ间的函数关系式及自变量的取值范围； 例3 已知二次函数的图象如图，
（3）在对称轴右侧的抛物线上是否存在点P使△ PAC为Rt△ ？若存在，求出所有符合条件的点P的坐标；若不存在，说明理由。解 ：设P（m，n）则ｎ＝ｍ２－ｍ－２１）当Ｒｔ△ ＰＡＣ是以ＰＣ为斜边时
　　有ＰＣ２＝ＰＡ２＋ＡＣ２
　即ｍ２＋（ｎ＋２）２＝（ｍ＋１）２＋ｎ２＋５
　把ｎ＝ｍ２－ｍ－２　代入得
　∴点Ｐ１（　　，　　）２）当Ｒｔ△ ＰＡＣ以ＰＡ为斜边时
　　则　ＰＡ２＝ＰＣ２＋ＡＣ２
　　　即（ｍ＋１）２＋ｎ２＝ｍ２＋（ｎ＋２）２＋５
　　把ｎ＝ｍ２－ｍ－２代入得
∴点Ｐ２（　　　，　　　）∴存在符合条件的点Ｐ，坐标为
　例3:如图，在一面靠墙的空地上用长为24米的篱笆，围成中间隔有二道篱笆的长方形花圃，设花圃的宽AB为x米，面积为S平方米。
(1)求S与x的函数关系式及自变量的取值范围；
(2)当x取何值时所围成的花圃面积最大，最大值是多少？
(3)若墙的最大可用长度为8米，则求围成花圃的最大面积。 解： (1) ∵ AB为x米、篱笆长为24米
∴ 花圃宽为（24－4x）米
(3) ∵墙的可用长度为8米
(2)当x＝ 时，S最大值＝ ＝36（平方米）∴ S＝x（24－4x）
＝－4x2＋24 x （0∴ 0<24－4x ≤8 4≤x<6∴当x＝4cm时，S最大值＝32 平方米例3、在矩形ABCD中，AB＝6cm，BC＝12cm，点P从点A出发，沿AB边向点B以1cm/秒的速度移动，同时，点Q从点B出发沿BC边向点C以2cm/秒的速度移动。如果P、Q两点在分别到达B、C两点后就停止移动，回答下列问题：
（1）运动开始后第几秒时，△PBQ的面积等于8cm2
（2）设运动开始后第t秒时，五边形APQCD的面积为Scm2，写出S与t的函数关系式，并指出自变量t的取值范围；
（3）t为何值时S最小？求出S的最小值。 例4:如图、等腰直角三角形的腰长和正方形的边长为4，等腰三角形以2米/秒的速度沿直线向正方形移动，直到AB与CD重合。设x秒时，三角形与正方形重叠部分的面积为y平方米.
(1)写出y与x的函数关系式及自变量的取值范围
(2)当重叠部分的面积是正方形的面积的一半时,三角形移动了多长时间?思考:如果继续向前移动,则重叠部分面积又会如何变化?作业：
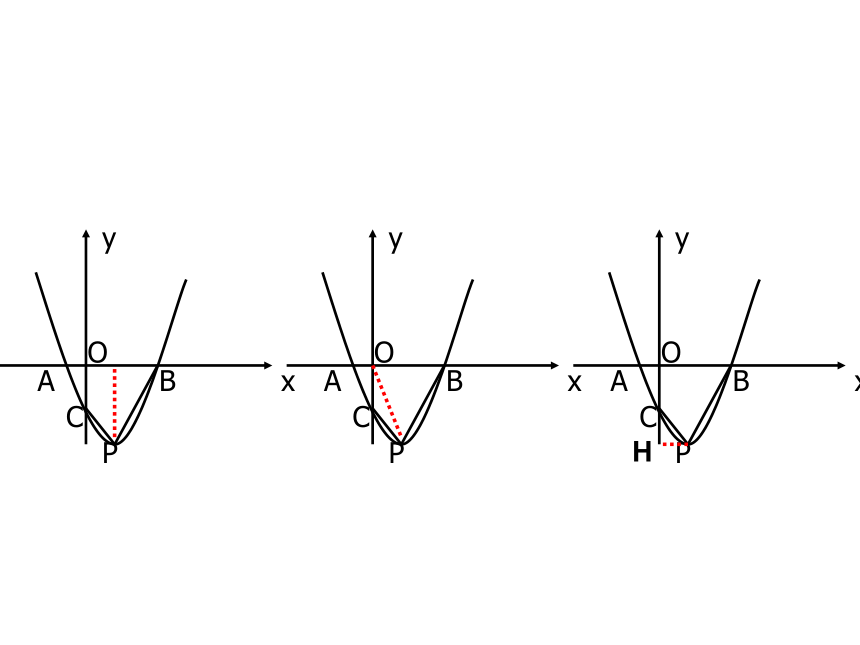
《第二章全效自测题》 如图所示，已知抛物线y=ax2+bx+c(a≠0)与x轴相交
于两点A（x1，0） B（x2，0）（x1 轴相交于点C，若抛物线顶点P的横坐标是1，A、B
两点间的距离为4，且△ABC的面积为6。（1）求点A和B的坐标（2）求此抛物线的解析式（3）求四边形ACPB的面积（4）设M（x，y）（其中0 是抛物线上的一个动点，试求
四边形OCMB的最大值，
及此时点M的坐标。.MNQ练习（1）已知函数y= -x2-x-4，当函数值y随x的增大而减小时，x的取值范围是___________
（2）二次函数y=mx2-3x+2m-m2的图象经过原点，则m= ____。X≤12（3）、已知二次函数y=2(x+1)2+1,(-2≤x≤1），则y的最小值是 ，y的最大值是 。19