2021-2022学年浙教版八年级数学下册4.5三角形的中位线 优生辅导练习题(word版含答案)
文档属性
| 名称 | 2021-2022学年浙教版八年级数学下册4.5三角形的中位线 优生辅导练习题(word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 242.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-17 13:17:33 | ||
图片预览



文档简介
2021-2022学年浙教版八年级数学下册《4.5三角形的中位线》优生辅导练习题(附答案)
一.选择题
1.如图,AD为△ABC的角平分线,BE⊥AD于E,F为BC中点,连接EF,若∠BAC=80°,∠EBD=20°,则∠EFD=( )
A.26° B.28° C.30° D.32°
2.如图,在△ABC中,∠A=90°,AC>AB>4,点D、E分别在边AB、AC上,BD=4,CE=3,取DE、BC的中点M、N,线段MN的长为( )
A.2.5 B.3 C.4 D.5
3.如图,DE是△ABC的中位线,∠ABC的角平分线交DE于点F,AB=8,BC=12,则EF的长为( )
A.1 B.1.5 C.2 D.2.5
4.如图,四边形ABCD中,∠A=90°,AB=12,AD=5,点M、N分别为线段BC、AB上的动点(含端点,但点M不与点B重合),点E、F分别为DM、MN的中点,则EF长度的可能为( )
A.2 B.5 C.7 D.9
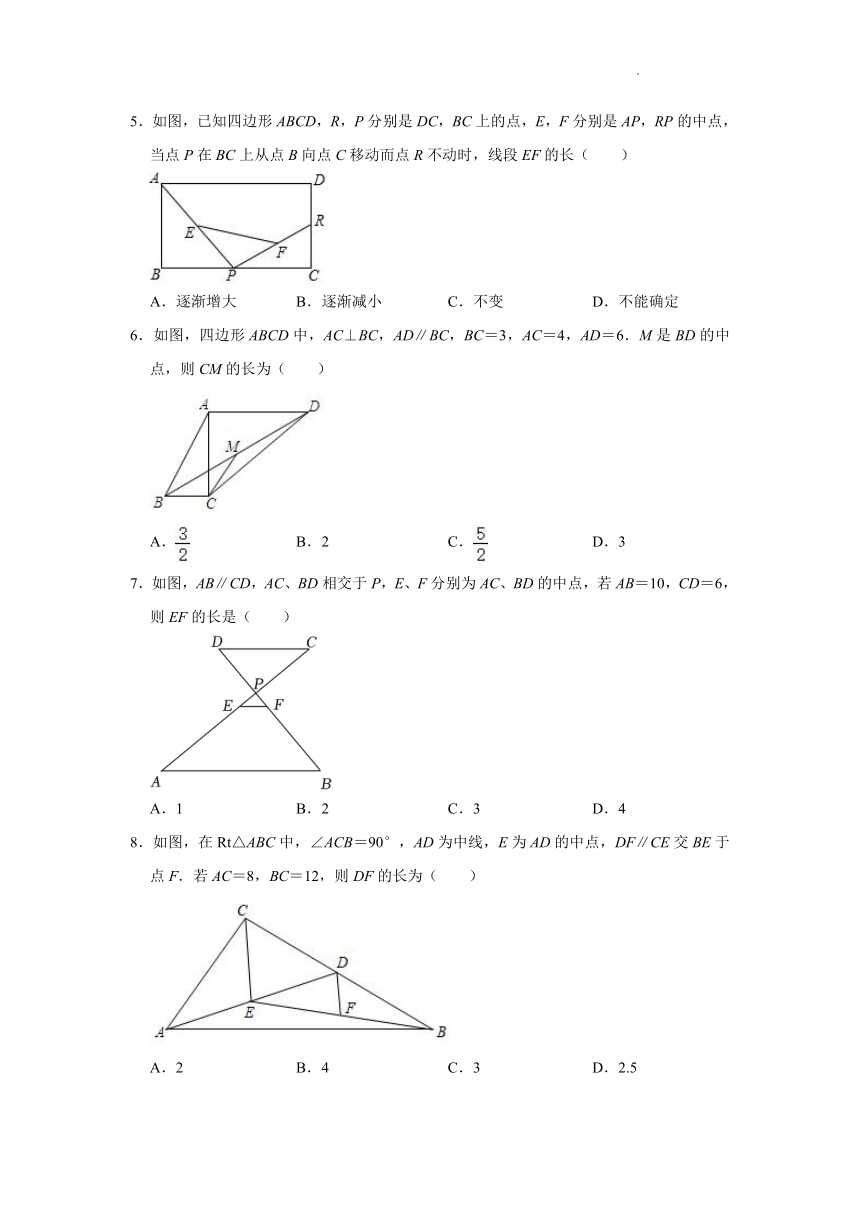
5.如图,已知四边形ABCD,R,P分别是DC,BC上的点,E,F分别是AP,RP的中点,当点P在BC上从点B向点C移动而点R不动时,线段EF的长( )
A.逐渐增大 B.逐渐减小 C.不变 D.不能确定
6.如图,四边形ABCD中,AC⊥BC,AD∥BC,BC=3,AC=4,AD=6.M是BD的中点,则CM的长为( )
A. B.2 C. D.3
7.如图,AB∥CD,AC、BD相交于P,E、F分别为AC、BD的中点,若AB=10,CD=6,则EF的长是( )
A.1 B.2 C.3 D.4
8.如图,在Rt△ABC中,∠ACB=90°,AD为中线,E为AD的中点,DF∥CE交BE于点F.若AC=8,BC=12,则DF的长为( )
A.2 B.4 C.3 D.2.5
二.填空题
9.如图,△ABC,点D,E在边BC上,∠ABC的平分线垂直AE,垂足为N,∠ACB的平分线垂直AD,垂足为M,若BC=16,MN=3,则△ABC的周长为 .
10.如图,在△ABC中,点D、E、F分别是各边的中点,若△ABC的面积为16cm2,则△DEF的面积是 cm2.
11.如图,在四边形ABCD中,P是对角线BD的中点,点E、F分别是AB、CD的中点,AD=BC,∠EPF=140°,则∠EFP的度数是 .
12.如图,△ABC是是以BC为底边的等腰三角形,点D,E,F分别是边AB,BC,AC的中点.若等腰△ABC的腰长为10cm,底边长为8cm,则:
(1)四边形ADEF的形状是 ;
(2)四边形ADEF的边长是 cm.
13.如图,M是△ABC的边BC的中点,AN平分∠BAC,且BN⊥AN,垂足为N,且AB=6,BC=10,MN=1.5,则△ABC的周长是 .
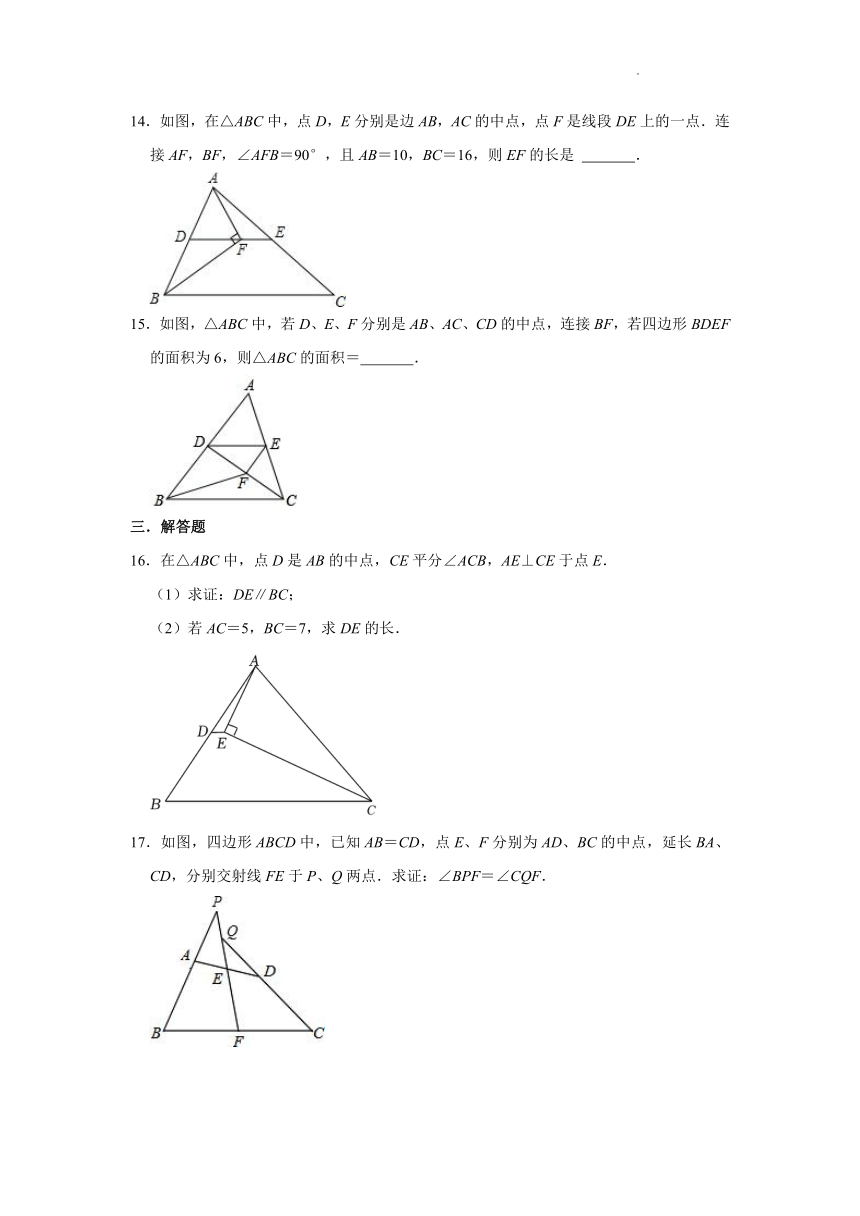
14.如图,在△ABC中,点D,E分别是边AB,AC的中点,点F是线段DE上的一点.连接AF,BF,∠AFB=90°,且AB=10,BC=16,则EF的长是 .
15.如图,△ABC中,若D、E、F分别是AB、AC、CD的中点,连接BF,若四边形BDEF的面积为6,则△ABC的面积= .
三.解答题
16.在△ABC中,点D是AB的中点,CE平分∠ACB,AE⊥CE于点E.
(1)求证:DE∥BC;
(2)若AC=5,BC=7,求DE的长.
17.如图,四边形ABCD中,已知AB=CD,点E、F分别为AD、BC的中点,延长BA、CD,分别交射线FE于P、Q两点.求证:∠BPF=∠CQF.
18.已知:如图,在四边形ABCD中,对角线AC、BD相交于O,且AC=BD,E、F分别是AB、CD的中点,E、F分别交BD、AC于点G、H.求证:OG=OH.
19.如图,点D、E是Rt△ABC两直角边AB、AC上的一点,连接BE,已知点F、G、H分别是DE、BE、BC的中点.
(1)求∠FGH度数;
(2)连CD,取CD中点M,连接GM,若BD=8,CE=6,求GM的长.
20.如图,等边△ABC的边长是4,D,E分别为AB,AC的中点,延长BC至点F,使CF=BC,连接CD和EF.
(1)求证:DE=CF;
(2)求EF的长;
(3)求四边形DEFC的面积.
21.如图,在△ABC中,D、E、F分别是AB、BC、AC的中点,AH⊥BC,垂足为H.
求证:(1)HD=EF.
(2)∠DHF=∠DEF.
22.观察探究,完成证明和填空.
如图,四边形ABCD中,点E、F、G、H分别是边AB、BC、CD、DA的中点,顺次连接E、F、G、H,得到的四边形EFGH叫中点四边形.
(1)求证:四边形EFGH是平行四边形;
(2)如图,当四边形ABCD变成等腰梯形时,它的中点四边形是菱形,请你探究并填空:
当四边形ABCD变成平行四边形时,它的中点四边形是 ;
当四边形ABCD变成矩形时,它的中点四边形是 ;
当四边形ABCD变成菱形时,它的中点四边形是 ;
当四边形ABCD变成正方形时,它的中点四边形是 ;
(3)根据以上观察探究,请你总结中点四边形的形状由原四边形的什么决定的?
参考答案
一.选择题
1.解:延长BE交AC于G,如图所示:
∵AD平分∠BAC,∠BAC=80°,
∴∠BAE=∠GAE=∠BAC=40°,
∵BE⊥AD,
∴∠BEA=∠GEA=90°,
∵AE=AE,
∴△ABE≌△AGE(ASA),
∴BE=GE,
∵F为BC的中点,
∴EF是△BCG的中位线,
∴EF∥GC,
∴∠EFD=∠C,
∵∠BEA=90°,
∴∠ABE=90°﹣∠BAE=90°﹣40°=50°,
∴∠ABC=∠ABE+∠EBD=50°+20°=70°,
∴∠EFD=∠C=180°﹣∠BAC﹣∠ABC=180°﹣80°﹣70°=30°,
故选:C.
2.解:作CH∥AB,连接DN并延长交CH于H,连接EH,
∵BD∥CH,
∴∠B=∠NCH,∠ECH+∠A=180°,
∵∠A=90°,
∴∠ECH=∠A=90°,
在△DNB和△HNC中,
,
∴△DNB≌△HNC(ASA),
∴CH=BD=4,DN=NH,
在Rt△CEH中,CH=4,CE=3,
∴EH===5,
∵DM=ME,DN=NH,
∴MN=EH=2.5,
故选:A.
3.解:连接AF并延长交BC于H,如图所示:
∵点D、E分别为边AB、AC的中点,
∴DE∥BC,DE=BC=6,AF=FH,
在△BFA和△BFH中,
,
∴△BFA≌△BFH(AAS),
∴BH=AB=8,
∵AD=DB,AF=FH,
∴DF是△ABH的中位线,
∴DF=BH=4,
∴EF=DE﹣DF=2,
故选:C.
4.解:连接DN,
∵ED=EM,MF=FN,
∴EF=DN,
∴DN最大时,EF最大,DN最小时,EF最小,
∵N与B重合时DN最大,
此时DN=DB===13,
∴EF的最大值为6.5.
∵∠A=90°,AD=5,
∴DN≥5,
∴EF≥2.5,
∴EF长度的可能为5;
故选:B.
5.解:连接AR.
∵E、F分别是AP、RP的中点,
∴EF为△APR的中位线,
∴EF=AR,
∵AR的长为定值,
∴线段EF的长不改变.
故选:C.
6.解:延长BC 到E 使BE=AD,则四边形ABED是平行四边形,∵BC=3,AD=6,
∴C是BE的中点,
∵M是BD的中点,
∴CM=DE=AB,
∵AC⊥BC,
∴AB===5,
∴CM=,
解法二:延长CM交AD于T.
∵AD∥BC,
∴∠MBC=∠MDT,
∵MD=MB,∠BMC=∠DMT,
∴△BMC≌△DMT(ASA),
∴CM=MT,DT=BC=3,
∵AD=6,
∴AT=3,
∵AC=4,∠CAT=90°,
∴CT===5,
∴CM=MT=CT=.
故选:C.
7.解:连接CF并延长,交AB于G,
∵AB∥DC,
∴∠D=∠B,
∵F为BD的中点,
∴DF=BF,
在△DFC和△BFG中,
,
∴△DFC≌△BFG(ASA),
∴BG=CD=6,CF=FG,
∴AG=AB﹣BG=4,
∵CF=FG,CE=EA,
∴EF=AG=×4=2,
故选:B.
8.解:∵AD为中线,BC=12,
∴CD=BC=×12=6,
在Rt△ACD中,AD===10,
∵∠ACB=90°,E为AD的中点,
∴CE=AD=5,
∵DF∥CE,D为BC的中点,
∴DF=CE=2.5,
故选:D.
二.填空题
9.解:在△BNA和△BNE中,
,
∴△BNA≌△BNE(ASA),
∴BE=BA,AN=NE,
同理,CD=CA,AM=MD,
∵AM=MD,AN=NE,MN=3,
∴DE=2MN=6,
∵BE+CD﹣BC=DE,
∴AB+AC=BC+DE=22,
∴△ABC的周长=AB+AC+BC=22+16=38,
故答案为:38.
10.解:∵点D、F分别是AB,AC的中点,
∴DF∥BC,DF=BC,
∴DF∥BE,
∵E是BC的中点,
∴BE=BC,
∴DF=BE,
∴四边形BEFD是平行四边形,
∴BD=EF,
在△BDE和△FED中,
,
∴△BDE≌△FED(SSS),
同理可证△DAF≌△FED,△EFC≌△FED,
即△BDE≌△DAF≌△EFC≌△FED,
∴S△DEF=S△ABC=×16=4(cm2),
故答案为:4.
11.解:∵P是BD的中点,E是AB的中点,
∴PE是△ABD的中位线,
∴PE=AD,
同理,PF=BC,
∵AD=BC,
∴PE=PF,
∴∠EFP=×(180°﹣∠EPF)=×(180°﹣140°)=20°,
故答案为:20°.
12.解:(1)∵点D,E,F分别是边AB,BC,AC的中点,
∴DE∥AC,DE=AC=AF,EF∥AB,EF=AB=AD,
∴四边形ADEF是平行四边形,
∵AB=AC,
∴DE=EF,
∴平行四边形ADEF是菱形,
故答案为:菱形;
(2)∵AB=10cm,
∴EF=5cm,即四边形ADEF的边长是5cm,
故答案为:5.
13.解:延长线段BN交AC于E.
∵AN平分∠BAC,
∴∠BAN=∠EAN,
∵BN⊥AN,
∴∠ANB=∠ANE=90°,
在△ABN和△AEN中,
,
∴△ABN≌△AEN(ASA),
∴AE=AB=6,BN=NE,
又∵M是△ABC的边BC的中点,
∴CE=2MN=2×1.5=3,
∴△ABC的周长是AB+BC+AC=6+10+6+3=25,
故答案为:25.
14.解:∵点D、E分别是边AB、AC的中点,
∴DE是△ABC的中位线,
∵BC=16,
∴DE=BC=8.
∵∠AFB=90°,D是AB的中点,AB=10,
∴DF=AB=5,
∴EF=DE﹣DF=8﹣5=3.
故答案为:3.
15.解:∵点F是CD的中点,
∴S△DEF=S△CEF,
设S△DEF=S△CEF=x,
∵D、E分别是AB、AC的中点,
∴S△ADE=S△CDE=2x,S△BDC=S△ADC=4x,S△BDF=2x,
∴S 四边形BDEF=3x.
∵S 四边形BDEF=6,
∴3x=6,
∴x=2,
∴S△ABC=2S△BDC=8x=16,
故答案为:16.
三.解答题
16.解:(1)延长AE交BC于F,
∵CE平分∠ACB,AE⊥CE于点E,
∴∠ACE=∠FCE,∠AEC=∠FEC=90°,
在△ACE和△FCE中,
,
∴△ACE≌△FCE.
∴AE=EF,
∵点D是AB的中点,
∴AD=BD,
∴DE是△ABF的中位线.
∴DE∥BC;
(2)∵△ACE≌△FCE,
∴CF=AC=5,
∵DE是△ABF的中位线.
∴DE=BF=(BC﹣AC)=(7﹣5)=1,
故DE的长为1.
17.证明:如图,连接BD,作BD的中点M,连接EM、FM.
∵点E是AD的中点,
∴在△ABD中,EM∥AB,EM=AB,
∴∠MEF=∠P
同理可证:FM∥CD,FM=CD.
∴∠MFQ=∠CQF,
又∵AB=CD,
∴EM=FM,
∴∠MEF=∠MFE,
∴∠P=∠CQF.
18.解:取BC边的中点M,连接EM,FM,
∵M、F分别是BC、CD的中点,
∴MF∥BD,MF=BD,
同理:ME∥AC,ME=AC,
∵AC=BD
∴ME=MF
∴∠MEF=∠MFE,
∵MF∥BD,
∴∠MFE=∠OGH,
同理,∠MEF=∠OHG,
∴∠OGH=∠OHG
∴OG=OH.
19.解:(1)∵F、G、H分别是DE、BE、BC的中点,
∴FG∥DB,GH∥EC.
∴∠DBE=∠FGE,∠EGH=∠AEG.
∠FGH=∠FGE+∠EGH=∠ABE+∠BEA=180°﹣∠A=180°﹣90°=90°.
(2)如图所示:连接FM、HM.
∵M、H分别是BC和DC的中点,
∴MH∥BD,MH=.
同理:GF∥BD,GF=.
∴四边形FGHM为平行四边形.
∵G、H、M分别是BE、BC、DC的中点,
∴GH==3,,
由(1)可知:∠FGH=90°,
∴四边形FGHM为矩形.
∴∠GHM=90°.
∴GM==5.
20.解:(1)在△ABC中,
∵D、E分别为AB、AC的中点,
∴DE为△ABC的中位线,
∴DE=BC,
∵CF=BC,
∴DE=CF.
(2)∵AC=BC,AD=BD,
∴CD⊥AB,
∵BC=4,BD=2,
∴CD==2,
∵DE∥CF,DE=CF,
∴四边形DEFC是平行四边形,
∴EF=CD=2.
(3)过点D作DH⊥BC于H.
∵∠DHC=90°,∠DCB=30°,
∴DH=DC=,
∵DE=CF=2,
∴S四边形DEFC=CF DH=2×=2.
21.(1)证明:在△ABC中,AH⊥BC,
∴∠AHB=90°,
∵D为AB中点,
∴DH=AB,
∵E,F分别为BC,AC边中点,
∴EF=AB,
∴DH=EF;
(2)∵D、E分别为AB、BC中点,
∴DE∥AC,DE=AC,
∵F为AC中点,
∴AF=AC,
∴DE=AF,
∴四边形DEFA为平行四边形,
∴∠DEF=∠BAC,
∵DH=AB=AD,
∴∠BAH=∠DHA,
∵F为AC中点,∠AHC=90°,
∴FH=AC=AF,
∴∠HAC=∠AHF,
∴∠DHA+∠AHF=∠DAH+∠FAH,
即∠DHF=∠BAC,
∴∠DHF=∠DEF.
22.(1)证明:连接BD.
∵E、H分别是AB、AD的中点,
∴EH是△ABD的中位线.
∴EH=BD,EH∥BD.
同理得FG=BD,FG∥BD.
∴EH=FG,EH∥FG.
∴四边形EFGH是平行四边形.
(2)填空依次为平行四边形,菱形,矩形,正方形;
(3)中点四边形的形状是由原四边形的对角线的关系决定的.
故答案为平行四边形、菱形、矩形、正方形.
一.选择题
1.如图,AD为△ABC的角平分线,BE⊥AD于E,F为BC中点,连接EF,若∠BAC=80°,∠EBD=20°,则∠EFD=( )
A.26° B.28° C.30° D.32°
2.如图,在△ABC中,∠A=90°,AC>AB>4,点D、E分别在边AB、AC上,BD=4,CE=3,取DE、BC的中点M、N,线段MN的长为( )
A.2.5 B.3 C.4 D.5
3.如图,DE是△ABC的中位线,∠ABC的角平分线交DE于点F,AB=8,BC=12,则EF的长为( )
A.1 B.1.5 C.2 D.2.5
4.如图,四边形ABCD中,∠A=90°,AB=12,AD=5,点M、N分别为线段BC、AB上的动点(含端点,但点M不与点B重合),点E、F分别为DM、MN的中点,则EF长度的可能为( )
A.2 B.5 C.7 D.9
5.如图,已知四边形ABCD,R,P分别是DC,BC上的点,E,F分别是AP,RP的中点,当点P在BC上从点B向点C移动而点R不动时,线段EF的长( )
A.逐渐增大 B.逐渐减小 C.不变 D.不能确定
6.如图,四边形ABCD中,AC⊥BC,AD∥BC,BC=3,AC=4,AD=6.M是BD的中点,则CM的长为( )
A. B.2 C. D.3
7.如图,AB∥CD,AC、BD相交于P,E、F分别为AC、BD的中点,若AB=10,CD=6,则EF的长是( )
A.1 B.2 C.3 D.4
8.如图,在Rt△ABC中,∠ACB=90°,AD为中线,E为AD的中点,DF∥CE交BE于点F.若AC=8,BC=12,则DF的长为( )
A.2 B.4 C.3 D.2.5
二.填空题
9.如图,△ABC,点D,E在边BC上,∠ABC的平分线垂直AE,垂足为N,∠ACB的平分线垂直AD,垂足为M,若BC=16,MN=3,则△ABC的周长为 .
10.如图,在△ABC中,点D、E、F分别是各边的中点,若△ABC的面积为16cm2,则△DEF的面积是 cm2.
11.如图,在四边形ABCD中,P是对角线BD的中点,点E、F分别是AB、CD的中点,AD=BC,∠EPF=140°,则∠EFP的度数是 .
12.如图,△ABC是是以BC为底边的等腰三角形,点D,E,F分别是边AB,BC,AC的中点.若等腰△ABC的腰长为10cm,底边长为8cm,则:
(1)四边形ADEF的形状是 ;
(2)四边形ADEF的边长是 cm.
13.如图,M是△ABC的边BC的中点,AN平分∠BAC,且BN⊥AN,垂足为N,且AB=6,BC=10,MN=1.5,则△ABC的周长是 .
14.如图,在△ABC中,点D,E分别是边AB,AC的中点,点F是线段DE上的一点.连接AF,BF,∠AFB=90°,且AB=10,BC=16,则EF的长是 .
15.如图,△ABC中,若D、E、F分别是AB、AC、CD的中点,连接BF,若四边形BDEF的面积为6,则△ABC的面积= .
三.解答题
16.在△ABC中,点D是AB的中点,CE平分∠ACB,AE⊥CE于点E.
(1)求证:DE∥BC;
(2)若AC=5,BC=7,求DE的长.
17.如图,四边形ABCD中,已知AB=CD,点E、F分别为AD、BC的中点,延长BA、CD,分别交射线FE于P、Q两点.求证:∠BPF=∠CQF.
18.已知:如图,在四边形ABCD中,对角线AC、BD相交于O,且AC=BD,E、F分别是AB、CD的中点,E、F分别交BD、AC于点G、H.求证:OG=OH.
19.如图,点D、E是Rt△ABC两直角边AB、AC上的一点,连接BE,已知点F、G、H分别是DE、BE、BC的中点.
(1)求∠FGH度数;
(2)连CD,取CD中点M,连接GM,若BD=8,CE=6,求GM的长.
20.如图,等边△ABC的边长是4,D,E分别为AB,AC的中点,延长BC至点F,使CF=BC,连接CD和EF.
(1)求证:DE=CF;
(2)求EF的长;
(3)求四边形DEFC的面积.
21.如图,在△ABC中,D、E、F分别是AB、BC、AC的中点,AH⊥BC,垂足为H.
求证:(1)HD=EF.
(2)∠DHF=∠DEF.
22.观察探究,完成证明和填空.
如图,四边形ABCD中,点E、F、G、H分别是边AB、BC、CD、DA的中点,顺次连接E、F、G、H,得到的四边形EFGH叫中点四边形.
(1)求证:四边形EFGH是平行四边形;
(2)如图,当四边形ABCD变成等腰梯形时,它的中点四边形是菱形,请你探究并填空:
当四边形ABCD变成平行四边形时,它的中点四边形是 ;
当四边形ABCD变成矩形时,它的中点四边形是 ;
当四边形ABCD变成菱形时,它的中点四边形是 ;
当四边形ABCD变成正方形时,它的中点四边形是 ;
(3)根据以上观察探究,请你总结中点四边形的形状由原四边形的什么决定的?
参考答案
一.选择题
1.解:延长BE交AC于G,如图所示:
∵AD平分∠BAC,∠BAC=80°,
∴∠BAE=∠GAE=∠BAC=40°,
∵BE⊥AD,
∴∠BEA=∠GEA=90°,
∵AE=AE,
∴△ABE≌△AGE(ASA),
∴BE=GE,
∵F为BC的中点,
∴EF是△BCG的中位线,
∴EF∥GC,
∴∠EFD=∠C,
∵∠BEA=90°,
∴∠ABE=90°﹣∠BAE=90°﹣40°=50°,
∴∠ABC=∠ABE+∠EBD=50°+20°=70°,
∴∠EFD=∠C=180°﹣∠BAC﹣∠ABC=180°﹣80°﹣70°=30°,
故选:C.
2.解:作CH∥AB,连接DN并延长交CH于H,连接EH,
∵BD∥CH,
∴∠B=∠NCH,∠ECH+∠A=180°,
∵∠A=90°,
∴∠ECH=∠A=90°,
在△DNB和△HNC中,
,
∴△DNB≌△HNC(ASA),
∴CH=BD=4,DN=NH,
在Rt△CEH中,CH=4,CE=3,
∴EH===5,
∵DM=ME,DN=NH,
∴MN=EH=2.5,
故选:A.
3.解:连接AF并延长交BC于H,如图所示:
∵点D、E分别为边AB、AC的中点,
∴DE∥BC,DE=BC=6,AF=FH,
在△BFA和△BFH中,
,
∴△BFA≌△BFH(AAS),
∴BH=AB=8,
∵AD=DB,AF=FH,
∴DF是△ABH的中位线,
∴DF=BH=4,
∴EF=DE﹣DF=2,
故选:C.
4.解:连接DN,
∵ED=EM,MF=FN,
∴EF=DN,
∴DN最大时,EF最大,DN最小时,EF最小,
∵N与B重合时DN最大,
此时DN=DB===13,
∴EF的最大值为6.5.
∵∠A=90°,AD=5,
∴DN≥5,
∴EF≥2.5,
∴EF长度的可能为5;
故选:B.
5.解:连接AR.
∵E、F分别是AP、RP的中点,
∴EF为△APR的中位线,
∴EF=AR,
∵AR的长为定值,
∴线段EF的长不改变.
故选:C.
6.解:延长BC 到E 使BE=AD,则四边形ABED是平行四边形,∵BC=3,AD=6,
∴C是BE的中点,
∵M是BD的中点,
∴CM=DE=AB,
∵AC⊥BC,
∴AB===5,
∴CM=,
解法二:延长CM交AD于T.
∵AD∥BC,
∴∠MBC=∠MDT,
∵MD=MB,∠BMC=∠DMT,
∴△BMC≌△DMT(ASA),
∴CM=MT,DT=BC=3,
∵AD=6,
∴AT=3,
∵AC=4,∠CAT=90°,
∴CT===5,
∴CM=MT=CT=.
故选:C.
7.解:连接CF并延长,交AB于G,
∵AB∥DC,
∴∠D=∠B,
∵F为BD的中点,
∴DF=BF,
在△DFC和△BFG中,
,
∴△DFC≌△BFG(ASA),
∴BG=CD=6,CF=FG,
∴AG=AB﹣BG=4,
∵CF=FG,CE=EA,
∴EF=AG=×4=2,
故选:B.
8.解:∵AD为中线,BC=12,
∴CD=BC=×12=6,
在Rt△ACD中,AD===10,
∵∠ACB=90°,E为AD的中点,
∴CE=AD=5,
∵DF∥CE,D为BC的中点,
∴DF=CE=2.5,
故选:D.
二.填空题
9.解:在△BNA和△BNE中,
,
∴△BNA≌△BNE(ASA),
∴BE=BA,AN=NE,
同理,CD=CA,AM=MD,
∵AM=MD,AN=NE,MN=3,
∴DE=2MN=6,
∵BE+CD﹣BC=DE,
∴AB+AC=BC+DE=22,
∴△ABC的周长=AB+AC+BC=22+16=38,
故答案为:38.
10.解:∵点D、F分别是AB,AC的中点,
∴DF∥BC,DF=BC,
∴DF∥BE,
∵E是BC的中点,
∴BE=BC,
∴DF=BE,
∴四边形BEFD是平行四边形,
∴BD=EF,
在△BDE和△FED中,
,
∴△BDE≌△FED(SSS),
同理可证△DAF≌△FED,△EFC≌△FED,
即△BDE≌△DAF≌△EFC≌△FED,
∴S△DEF=S△ABC=×16=4(cm2),
故答案为:4.
11.解:∵P是BD的中点,E是AB的中点,
∴PE是△ABD的中位线,
∴PE=AD,
同理,PF=BC,
∵AD=BC,
∴PE=PF,
∴∠EFP=×(180°﹣∠EPF)=×(180°﹣140°)=20°,
故答案为:20°.
12.解:(1)∵点D,E,F分别是边AB,BC,AC的中点,
∴DE∥AC,DE=AC=AF,EF∥AB,EF=AB=AD,
∴四边形ADEF是平行四边形,
∵AB=AC,
∴DE=EF,
∴平行四边形ADEF是菱形,
故答案为:菱形;
(2)∵AB=10cm,
∴EF=5cm,即四边形ADEF的边长是5cm,
故答案为:5.
13.解:延长线段BN交AC于E.
∵AN平分∠BAC,
∴∠BAN=∠EAN,
∵BN⊥AN,
∴∠ANB=∠ANE=90°,
在△ABN和△AEN中,
,
∴△ABN≌△AEN(ASA),
∴AE=AB=6,BN=NE,
又∵M是△ABC的边BC的中点,
∴CE=2MN=2×1.5=3,
∴△ABC的周长是AB+BC+AC=6+10+6+3=25,
故答案为:25.
14.解:∵点D、E分别是边AB、AC的中点,
∴DE是△ABC的中位线,
∵BC=16,
∴DE=BC=8.
∵∠AFB=90°,D是AB的中点,AB=10,
∴DF=AB=5,
∴EF=DE﹣DF=8﹣5=3.
故答案为:3.
15.解:∵点F是CD的中点,
∴S△DEF=S△CEF,
设S△DEF=S△CEF=x,
∵D、E分别是AB、AC的中点,
∴S△ADE=S△CDE=2x,S△BDC=S△ADC=4x,S△BDF=2x,
∴S 四边形BDEF=3x.
∵S 四边形BDEF=6,
∴3x=6,
∴x=2,
∴S△ABC=2S△BDC=8x=16,
故答案为:16.
三.解答题
16.解:(1)延长AE交BC于F,
∵CE平分∠ACB,AE⊥CE于点E,
∴∠ACE=∠FCE,∠AEC=∠FEC=90°,
在△ACE和△FCE中,
,
∴△ACE≌△FCE.
∴AE=EF,
∵点D是AB的中点,
∴AD=BD,
∴DE是△ABF的中位线.
∴DE∥BC;
(2)∵△ACE≌△FCE,
∴CF=AC=5,
∵DE是△ABF的中位线.
∴DE=BF=(BC﹣AC)=(7﹣5)=1,
故DE的长为1.
17.证明:如图,连接BD,作BD的中点M,连接EM、FM.
∵点E是AD的中点,
∴在△ABD中,EM∥AB,EM=AB,
∴∠MEF=∠P
同理可证:FM∥CD,FM=CD.
∴∠MFQ=∠CQF,
又∵AB=CD,
∴EM=FM,
∴∠MEF=∠MFE,
∴∠P=∠CQF.
18.解:取BC边的中点M,连接EM,FM,
∵M、F分别是BC、CD的中点,
∴MF∥BD,MF=BD,
同理:ME∥AC,ME=AC,
∵AC=BD
∴ME=MF
∴∠MEF=∠MFE,
∵MF∥BD,
∴∠MFE=∠OGH,
同理,∠MEF=∠OHG,
∴∠OGH=∠OHG
∴OG=OH.
19.解:(1)∵F、G、H分别是DE、BE、BC的中点,
∴FG∥DB,GH∥EC.
∴∠DBE=∠FGE,∠EGH=∠AEG.
∠FGH=∠FGE+∠EGH=∠ABE+∠BEA=180°﹣∠A=180°﹣90°=90°.
(2)如图所示:连接FM、HM.
∵M、H分别是BC和DC的中点,
∴MH∥BD,MH=.
同理:GF∥BD,GF=.
∴四边形FGHM为平行四边形.
∵G、H、M分别是BE、BC、DC的中点,
∴GH==3,,
由(1)可知:∠FGH=90°,
∴四边形FGHM为矩形.
∴∠GHM=90°.
∴GM==5.
20.解:(1)在△ABC中,
∵D、E分别为AB、AC的中点,
∴DE为△ABC的中位线,
∴DE=BC,
∵CF=BC,
∴DE=CF.
(2)∵AC=BC,AD=BD,
∴CD⊥AB,
∵BC=4,BD=2,
∴CD==2,
∵DE∥CF,DE=CF,
∴四边形DEFC是平行四边形,
∴EF=CD=2.
(3)过点D作DH⊥BC于H.
∵∠DHC=90°,∠DCB=30°,
∴DH=DC=,
∵DE=CF=2,
∴S四边形DEFC=CF DH=2×=2.
21.(1)证明:在△ABC中,AH⊥BC,
∴∠AHB=90°,
∵D为AB中点,
∴DH=AB,
∵E,F分别为BC,AC边中点,
∴EF=AB,
∴DH=EF;
(2)∵D、E分别为AB、BC中点,
∴DE∥AC,DE=AC,
∵F为AC中点,
∴AF=AC,
∴DE=AF,
∴四边形DEFA为平行四边形,
∴∠DEF=∠BAC,
∵DH=AB=AD,
∴∠BAH=∠DHA,
∵F为AC中点,∠AHC=90°,
∴FH=AC=AF,
∴∠HAC=∠AHF,
∴∠DHA+∠AHF=∠DAH+∠FAH,
即∠DHF=∠BAC,
∴∠DHF=∠DEF.
22.(1)证明:连接BD.
∵E、H分别是AB、AD的中点,
∴EH是△ABD的中位线.
∴EH=BD,EH∥BD.
同理得FG=BD,FG∥BD.
∴EH=FG,EH∥FG.
∴四边形EFGH是平行四边形.
(2)填空依次为平行四边形,菱形,矩形,正方形;
(3)中点四边形的形状是由原四边形的对角线的关系决定的.
故答案为平行四边形、菱形、矩形、正方形.
同课章节目录
- 第一章 二次根式
- 1.1 二次根式
- 1.2 二次根式的性质
- 1.3 二次根式的运算
- 第二章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程的应用
- 2.4 一元二次方程根与系数的关系(选学)
- 第三章 数据分析初步
- 3.1 平均数
- 3.2 中位数和众数
- 3.3 方差和标准差
- 第四章 平行四边形
- 4.1 多边形
- 4.2 平行四边形
- 4.3 中心对称
- 4.4 平行四边形的判定
- 4.5 三角形的中位线
- 4.6 反证法
- 第五章 特殊平行四边形
- 5.1 矩形
- 5.2 菱形
- 5.3 正方形
- 第六章 反比例函数
- 6.1 反比例函数
- 6.2 反比例函数的图象和性质
- 6.3 反比例函数的应用
