3.1 投影同步练习卷(含答案)
图片预览


文档简介
浙教版九年级数学3.1投影巩固练习卷
一、单选题
1.下列四幅图中,能表示两棵树在同一时刻太阳光下的影子的图是( )
A. B.
C. D.
2.如图,正方形纸板的一条对角线重直于地面,纸板上方的灯(看作一个点)与这条对角线所确定的平面垂直于纸板,在灯光照射下,正方形纸板在地面上形成的影子的形状可以是( )
A. B. C. D.
3.如图是一根电线杆在一天中不同时刻的影长图,试按其 天中发生的先后顺序排列,正确的是( )
A.①②③④ B.④①③② C.④②③① D.④③②①
4.在同一时刻,身高1.8米的小强在阳光下的影长为0.9米,一棵大树的影长为4.6米,则树的高度为( )
A.9.8米 B.9.2米 C.8.2米 D.2.3米
5.下列投影中,是平行投影的是( )
A.路灯下行人的影子 B.太阳光下楼房的影子
C.台灯下书本的影子 D.在手电筒照射下纸片的影子
6.下列图形是平行投影的是( )
A. B.
C. D.
7.如图是王老师展示的他昨天画的一幅写生画,他让四个学生猜测他画这幅画的时间.根据王老师标出的方向,下列给出的时间比较接近的是( )
A.小丽说:“早上8点” B.小强说:“中午12点”
C.小刚说:“下午3点” D.小明说:“哪个时间段都行”
8.如图,夜间小明在路灯下由甲处走到乙处,他在地面上的影子( )
A.先变长后变短 B.先变短后变长
C.逐渐变短 D.逐渐变长
9.下列命题中真命题的个数为( )
①正方形的平行投影一定是菱形;②平行四边形的平行投影一定是平行四边形;③三角形的平行投影一定是三角形.
A.1 B.2 C.3 D.0
10.小乐用一块长方形硬纸板在阳光下做投影实验,通过观察,发现这块长方形硬纸板在平整的地面上不可能出现的投影是( )
A.三角形 B.线段 C.长方形 D.平行四边形
二、填空题
11.小亮的身高1.8m,他在阳光下的影长为0.6m;同一时刻,学校的旗杆影长为3m,则该旗杆的高度是 .
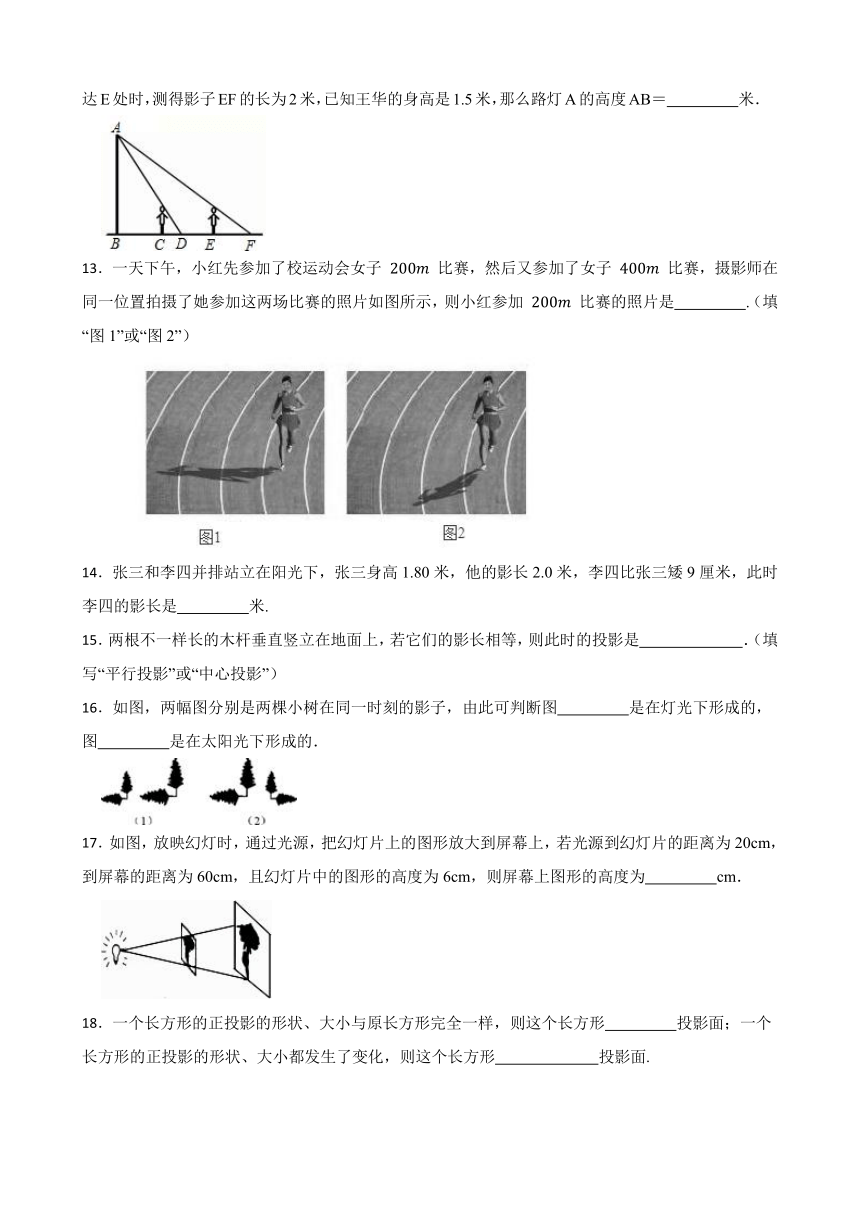
12.如图,王华晚上由路灯A下的B处走到C处时,测得影子CD的长为1米,继续往前走3米到达E处时,测得影子EF的长为2米,已知王华的身高是1.5米,那么路灯A的高度AB= 米.
13.一天下午,小红先参加了校运动会女子 比赛,然后又参加了女子 比赛,摄影师在同一位置拍摄了她参加这两场比赛的照片如图所示,则小红参加 比赛的照片是 .(填“图1”或“图2”)
14.张三和李四并排站立在阳光下,张三身高1.80米,他的影长2.0米,李四比张三矮9厘米,此时李四的影长是 米.
15.两根不一样长的木杆垂直竖立在地面上,若它们的影长相等,则此时的投影是 .(填写“平行投影”或“中心投影”)
16.如图,两幅图分别是两棵小树在同一时刻的影子,由此可判断图 是在灯光下形成的,图 是在太阳光下形成的.
17.如图,放映幻灯时,通过光源,把幻灯片上的图形放大到屏幕上,若光源到幻灯片的距离为20cm,到屏幕的距离为60cm,且幻灯片中的图形的高度为6cm,则屏幕上图形的高度为 cm.
18.一个长方形的正投影的形状、大小与原长方形完全一样,则这个长方形 投影面;一个长方形的正投影的形状、大小都发生了变化,则这个长方形 投影面.
三、解答题
19.如图,小军、小珠之间的距离为2.7m,他们在同一盏路灯下的影长分别为1.8m,1.5m,已知小军、小珠的身高分别为1.8m,1.5m,求路灯的高.
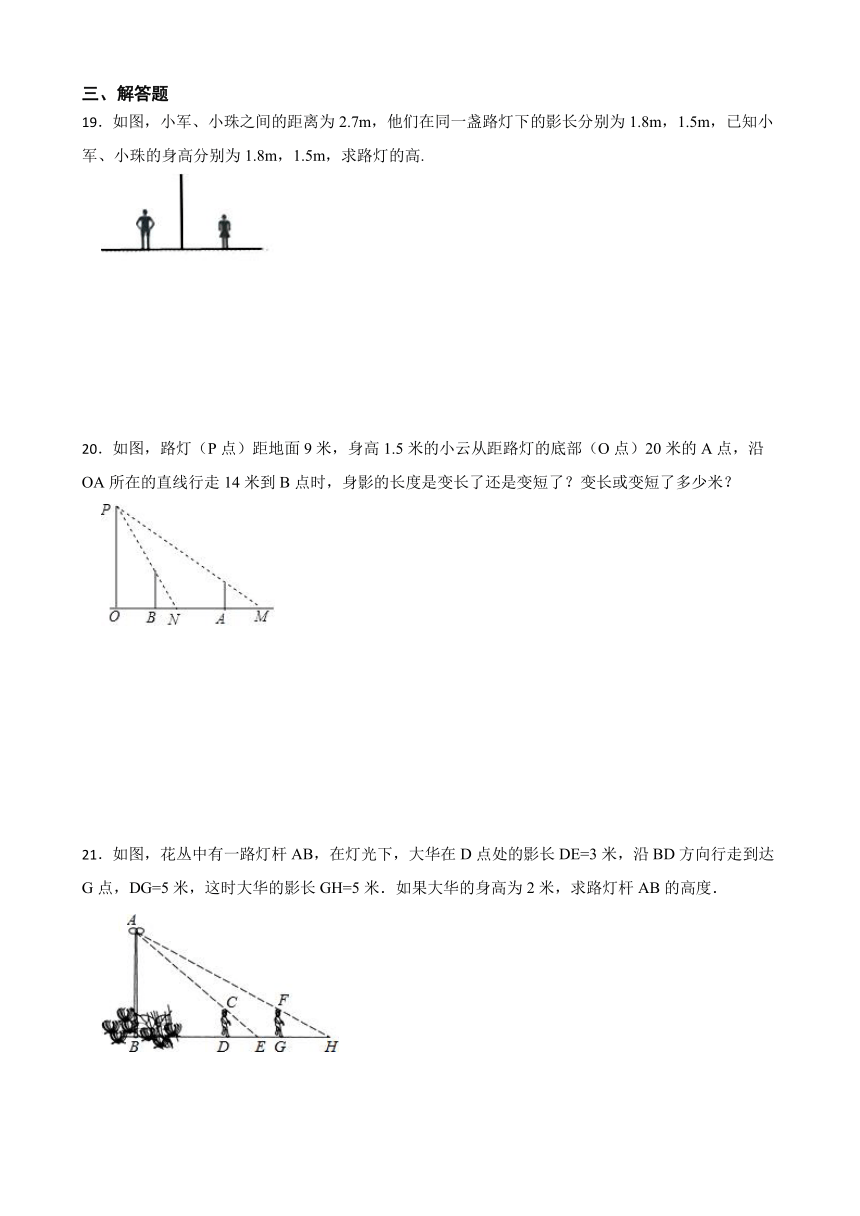
20.如图,路灯(P点)距地面9米,身高1.5米的小云从距路灯的底部(O点)20米的A点,沿OA所在的直线行走14米到B点时,身影的长度是变长了还是变短了?变长或变短了多少米?
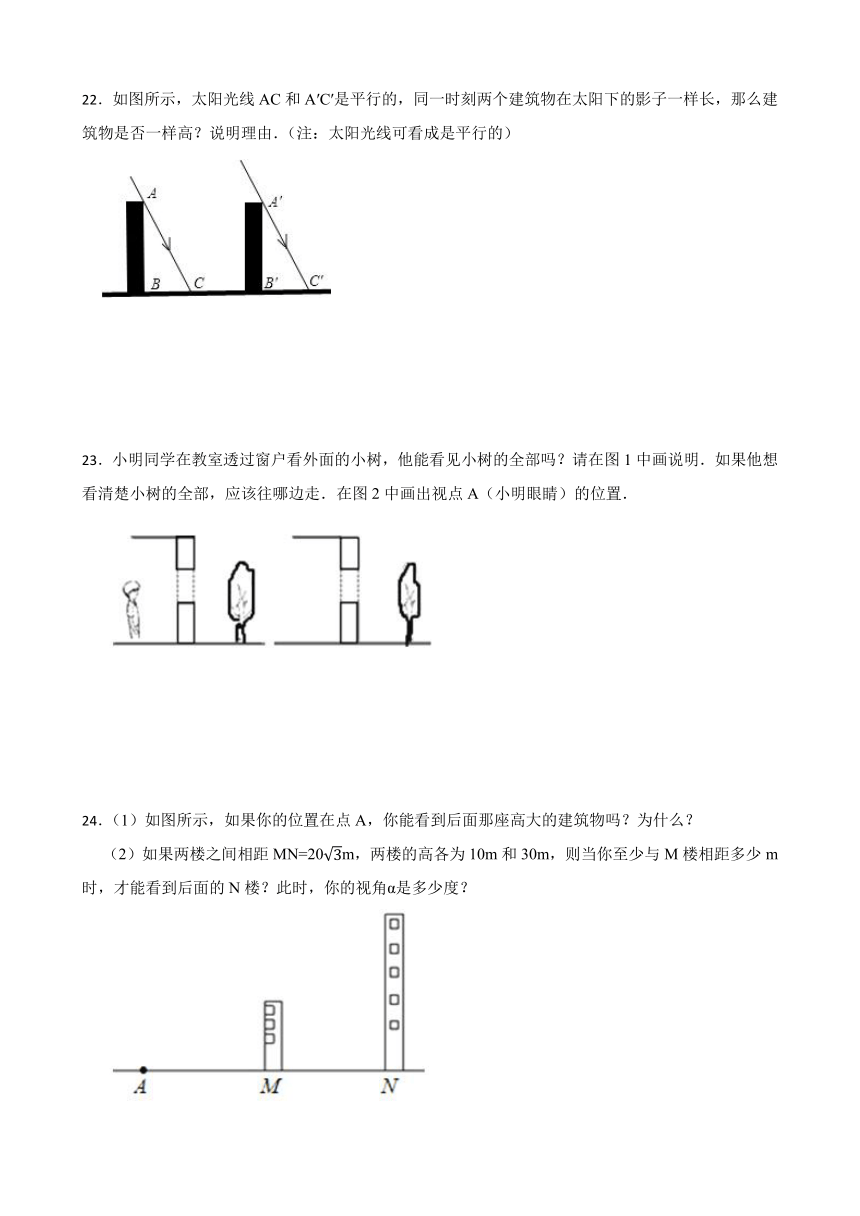
21.如图,花丛中有一路灯杆AB,在灯光下,大华在D点处的影长DE=3米,沿BD方向行走到达G点,DG=5米,这时大华的影长GH=5米.如果大华的身高为2米,求路灯杆AB的高度.
22.如图所示,太阳光线AC和A′C′是平行的,同一时刻两个建筑物在太阳下的影子一样长,那么建筑物是否一样高?说明理由.(注:太阳光线可看成是平行的)
23.小明同学在教室透过窗户看外面的小树,他能看见小树的全部吗?请在图1中画说明.如果他想看清楚小树的全部,应该往哪边走.在图2中画出视点A(小明眼睛)的位置.
24.(1)如图所示,如果你的位置在点A,你能看到后面那座高大的建筑物吗?为什么?
(2)如果两楼之间相距MN=20m,两楼的高各为10m和30m,则当你至少与M楼相距多少m时,才能看到后面的N楼?此时,你的视角α是多少度?
25.如图,阳光通过窗口照到教室内,竖直窗框在地面上留下2.1m长的影子如图所示,已知窗框的影子DE到窗下墙脚的距离CE=3.9m,窗口底边离地面的距离BC=1.2m,试求窗口的高度.(即AB的值)
答案解析部分
1.【答案】C
2.【答案】D
3.【答案】B
4.【答案】B
5.【答案】B
6.【答案】B
7.【答案】C
8.【答案】B
9.【答案】D
10.【答案】A
11.【答案】9m
12.【答案】6
13.【答案】图2
14.【答案】1.9
15.【答案】中心投影
16.【答案】(2);(1)
17.【答案】18
18.【答案】//;不平行于
19.【答案】解:如图,在Rt△CDE中,CD=DE=1.8m,
在Rt△MNF中,MN=NF=1.5m,
∵∠CDE=∠MNF=90°,
∴∠E=∠F=45°,
∴AB=EB=BF,
∴DB=AB﹣1.8,BN=AB﹣1.5,
∵DN=2.7m,
∴2AB﹣1.8﹣1.5=2.7,
∴AB=3(m),
∴路灯的高为3m.
20.【答案】解:∵∠MAC=∠MOP=90°,
∠AMC=∠OMP,
∴△MAC∽△MOP,
∴ = ,
即 = ,
解得,MA=4米;
同理,由△NBD∽△NOP,可求得NB=1.2米,
则马晓明的身影变短了4﹣1.2=2.8米.
∴变短了,短了2.8米.
21.【答案】解:∵CD∥AB,
∴△EAB∽△ECD,
∴ ,即 = ①,
∵FG∥AB,
∴△HFG∽△HAB,
∴ ,即 = ②,
由①②得 = ,
解得BD=7.5,
∴ = ,解得:AB=7.
答:路灯杆AB的高度为7m
22.【答案】解:建筑物一样高.
证明:∵AB⊥BC,A′B′⊥B′C′,
∴∠ABC=∠A′B′C′=90°,
∵AC∥A′C′,
∴∠ACB=∠A′C′B′,
在△ABC和△A′B′C′中,
,
∴△ABC≌△A′B′C′(ASA)
∴AB=A′B′.
即建筑物一样高
23.【答案】解:如图所示:他不能看见小树的全部,
小明应该往前(填前或后)走,
故答案为:前.
24.【答案】解:(1)所作图形如下:
所以能看见后面的大楼,因为大楼没有处在盲区.
(2)
由题意得,MN=20m,FM=10m,EN=30m,
设AM=x,则=,即=,
解得:x=10,即AM=10米.
tanα===,可得α=30°.
答:当你至少与M楼相距10m时,才能看到后面的N楼,此时,你的视角α=30°.
25.【答案】解:由于阳光是平行光线,即AE∥BD,
所以∠AEC=∠BDC.又因为∠C是公共角,
所以△AEC∽△BDC,从而有=.
又AC=AB+BC,DC=EC﹣ED,EC=3.9,ED=2.1,BC=1.2,
于是有=,解得AB=1.4(m).
答:窗口的高度为1.4m.
一、单选题
1.下列四幅图中,能表示两棵树在同一时刻太阳光下的影子的图是( )
A. B.
C. D.
2.如图,正方形纸板的一条对角线重直于地面,纸板上方的灯(看作一个点)与这条对角线所确定的平面垂直于纸板,在灯光照射下,正方形纸板在地面上形成的影子的形状可以是( )
A. B. C. D.
3.如图是一根电线杆在一天中不同时刻的影长图,试按其 天中发生的先后顺序排列,正确的是( )
A.①②③④ B.④①③② C.④②③① D.④③②①
4.在同一时刻,身高1.8米的小强在阳光下的影长为0.9米,一棵大树的影长为4.6米,则树的高度为( )
A.9.8米 B.9.2米 C.8.2米 D.2.3米
5.下列投影中,是平行投影的是( )
A.路灯下行人的影子 B.太阳光下楼房的影子
C.台灯下书本的影子 D.在手电筒照射下纸片的影子
6.下列图形是平行投影的是( )
A. B.
C. D.
7.如图是王老师展示的他昨天画的一幅写生画,他让四个学生猜测他画这幅画的时间.根据王老师标出的方向,下列给出的时间比较接近的是( )
A.小丽说:“早上8点” B.小强说:“中午12点”
C.小刚说:“下午3点” D.小明说:“哪个时间段都行”
8.如图,夜间小明在路灯下由甲处走到乙处,他在地面上的影子( )
A.先变长后变短 B.先变短后变长
C.逐渐变短 D.逐渐变长
9.下列命题中真命题的个数为( )
①正方形的平行投影一定是菱形;②平行四边形的平行投影一定是平行四边形;③三角形的平行投影一定是三角形.
A.1 B.2 C.3 D.0
10.小乐用一块长方形硬纸板在阳光下做投影实验,通过观察,发现这块长方形硬纸板在平整的地面上不可能出现的投影是( )
A.三角形 B.线段 C.长方形 D.平行四边形
二、填空题
11.小亮的身高1.8m,他在阳光下的影长为0.6m;同一时刻,学校的旗杆影长为3m,则该旗杆的高度是 .
12.如图,王华晚上由路灯A下的B处走到C处时,测得影子CD的长为1米,继续往前走3米到达E处时,测得影子EF的长为2米,已知王华的身高是1.5米,那么路灯A的高度AB= 米.
13.一天下午,小红先参加了校运动会女子 比赛,然后又参加了女子 比赛,摄影师在同一位置拍摄了她参加这两场比赛的照片如图所示,则小红参加 比赛的照片是 .(填“图1”或“图2”)
14.张三和李四并排站立在阳光下,张三身高1.80米,他的影长2.0米,李四比张三矮9厘米,此时李四的影长是 米.
15.两根不一样长的木杆垂直竖立在地面上,若它们的影长相等,则此时的投影是 .(填写“平行投影”或“中心投影”)
16.如图,两幅图分别是两棵小树在同一时刻的影子,由此可判断图 是在灯光下形成的,图 是在太阳光下形成的.
17.如图,放映幻灯时,通过光源,把幻灯片上的图形放大到屏幕上,若光源到幻灯片的距离为20cm,到屏幕的距离为60cm,且幻灯片中的图形的高度为6cm,则屏幕上图形的高度为 cm.
18.一个长方形的正投影的形状、大小与原长方形完全一样,则这个长方形 投影面;一个长方形的正投影的形状、大小都发生了变化,则这个长方形 投影面.
三、解答题
19.如图,小军、小珠之间的距离为2.7m,他们在同一盏路灯下的影长分别为1.8m,1.5m,已知小军、小珠的身高分别为1.8m,1.5m,求路灯的高.
20.如图,路灯(P点)距地面9米,身高1.5米的小云从距路灯的底部(O点)20米的A点,沿OA所在的直线行走14米到B点时,身影的长度是变长了还是变短了?变长或变短了多少米?
21.如图,花丛中有一路灯杆AB,在灯光下,大华在D点处的影长DE=3米,沿BD方向行走到达G点,DG=5米,这时大华的影长GH=5米.如果大华的身高为2米,求路灯杆AB的高度.
22.如图所示,太阳光线AC和A′C′是平行的,同一时刻两个建筑物在太阳下的影子一样长,那么建筑物是否一样高?说明理由.(注:太阳光线可看成是平行的)
23.小明同学在教室透过窗户看外面的小树,他能看见小树的全部吗?请在图1中画说明.如果他想看清楚小树的全部,应该往哪边走.在图2中画出视点A(小明眼睛)的位置.
24.(1)如图所示,如果你的位置在点A,你能看到后面那座高大的建筑物吗?为什么?
(2)如果两楼之间相距MN=20m,两楼的高各为10m和30m,则当你至少与M楼相距多少m时,才能看到后面的N楼?此时,你的视角α是多少度?
25.如图,阳光通过窗口照到教室内,竖直窗框在地面上留下2.1m长的影子如图所示,已知窗框的影子DE到窗下墙脚的距离CE=3.9m,窗口底边离地面的距离BC=1.2m,试求窗口的高度.(即AB的值)
答案解析部分
1.【答案】C
2.【答案】D
3.【答案】B
4.【答案】B
5.【答案】B
6.【答案】B
7.【答案】C
8.【答案】B
9.【答案】D
10.【答案】A
11.【答案】9m
12.【答案】6
13.【答案】图2
14.【答案】1.9
15.【答案】中心投影
16.【答案】(2);(1)
17.【答案】18
18.【答案】//;不平行于
19.【答案】解:如图,在Rt△CDE中,CD=DE=1.8m,
在Rt△MNF中,MN=NF=1.5m,
∵∠CDE=∠MNF=90°,
∴∠E=∠F=45°,
∴AB=EB=BF,
∴DB=AB﹣1.8,BN=AB﹣1.5,
∵DN=2.7m,
∴2AB﹣1.8﹣1.5=2.7,
∴AB=3(m),
∴路灯的高为3m.
20.【答案】解:∵∠MAC=∠MOP=90°,
∠AMC=∠OMP,
∴△MAC∽△MOP,
∴ = ,
即 = ,
解得,MA=4米;
同理,由△NBD∽△NOP,可求得NB=1.2米,
则马晓明的身影变短了4﹣1.2=2.8米.
∴变短了,短了2.8米.
21.【答案】解:∵CD∥AB,
∴△EAB∽△ECD,
∴ ,即 = ①,
∵FG∥AB,
∴△HFG∽△HAB,
∴ ,即 = ②,
由①②得 = ,
解得BD=7.5,
∴ = ,解得:AB=7.
答:路灯杆AB的高度为7m
22.【答案】解:建筑物一样高.
证明:∵AB⊥BC,A′B′⊥B′C′,
∴∠ABC=∠A′B′C′=90°,
∵AC∥A′C′,
∴∠ACB=∠A′C′B′,
在△ABC和△A′B′C′中,
,
∴△ABC≌△A′B′C′(ASA)
∴AB=A′B′.
即建筑物一样高
23.【答案】解:如图所示:他不能看见小树的全部,
小明应该往前(填前或后)走,
故答案为:前.
24.【答案】解:(1)所作图形如下:
所以能看见后面的大楼,因为大楼没有处在盲区.
(2)
由题意得,MN=20m,FM=10m,EN=30m,
设AM=x,则=,即=,
解得:x=10,即AM=10米.
tanα===,可得α=30°.
答:当你至少与M楼相距10m时,才能看到后面的N楼,此时,你的视角α=30°.
25.【答案】解:由于阳光是平行光线,即AE∥BD,
所以∠AEC=∠BDC.又因为∠C是公共角,
所以△AEC∽△BDC,从而有=.
又AC=AB+BC,DC=EC﹣ED,EC=3.9,ED=2.1,BC=1.2,
于是有=,解得AB=1.4(m).
答:窗口的高度为1.4m.
