第三章 投影与三视图单元测试题(含答案)
文档属性
| 名称 | 第三章 投影与三视图单元测试题(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 201.7KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-16 21:26:35 | ||
图片预览


文档简介
浙教版九年级数学第三章投影与三视图单元练习卷
一、单选题
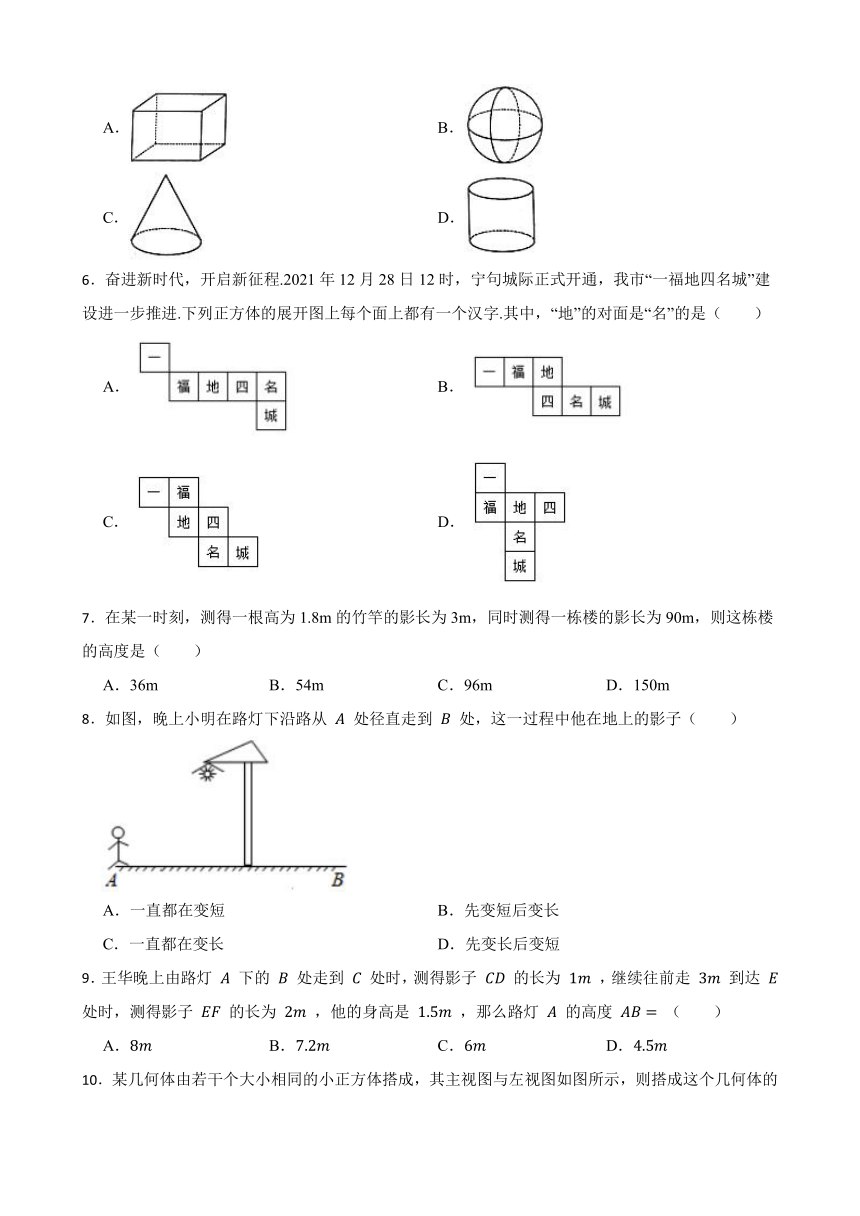
1.将弧长为2πcm、圆心角为120°的扇形围成一个圆锥的侧面,则这个圆锥的高是( )
A. cm B.2 cm C.2cm D. cm
2.如图,该几何体的主视图是( )
A. B.
C. D.
3.如图,一个圆锥形漏斗的底面半径OA=5cm,高OC=12cm.则它的侧面积是( )
A.130cm2 B.65πcm2 C.60πcm2 D.30cm2
4.如图,是一个小正方体的展开图,把展开图折叠成小正方体后,有“三”字一面的相对面上的字是( )
A.高 B.同 C.创 D.安
5.下列几何体的三视图中,俯视图与主视图一定一致的是( )
A. B.
C. D.
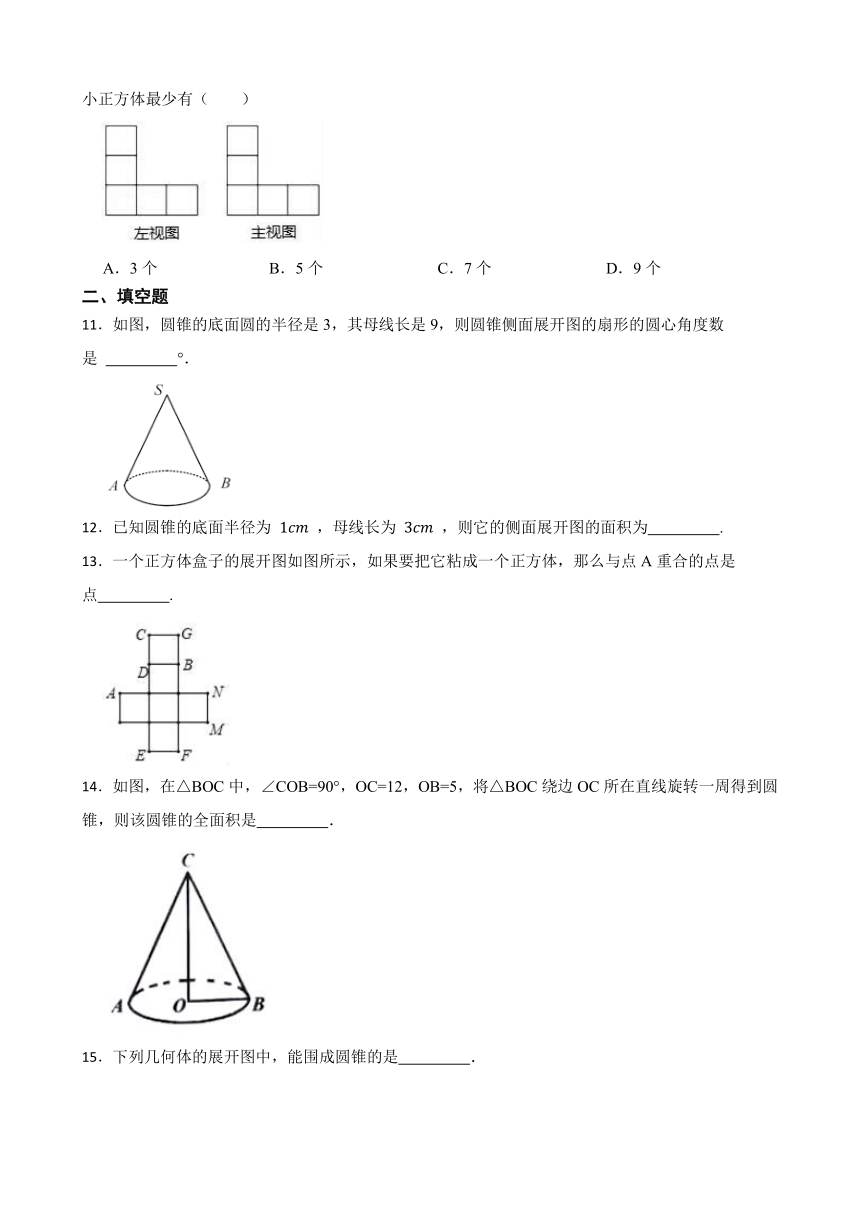
6.奋进新时代,开启新征程.2021年12月28日12时,宁句城际正式开通,我市“一福地四名城”建设进一步推进.下列正方体的展开图上每个面上都有一个汉字.其中,“地”的对面是“名”的是( )
A. B.
C. D.
7.在某一时刻,测得一根高为1.8m的竹竿的影长为3m,同时测得一栋楼的影长为90m,则这栋楼的高度是( )
A.36m B.54m C.96m D.150m
8.如图,晚上小明在路灯下沿路从 处径直走到 处,这一过程中他在地上的影子( )
A.一直都在变短 B.先变短后变长
C.一直都在变长 D.先变长后变短
9.王华晚上由路灯 下的 处走到 处时,测得影子 的长为 ,继续往前走 到达 处时,测得影子 的长为 ,他的身高是 ,那么路灯 的高度 ( )
A. B. C. D.
10.某几何体由若干个大小相同的小正方体搭成,其主视图与左视图如图所示,则搭成这个几何体的小正方体最少有( )
A.3个 B.5个 C.7个 D.9个
二、填空题
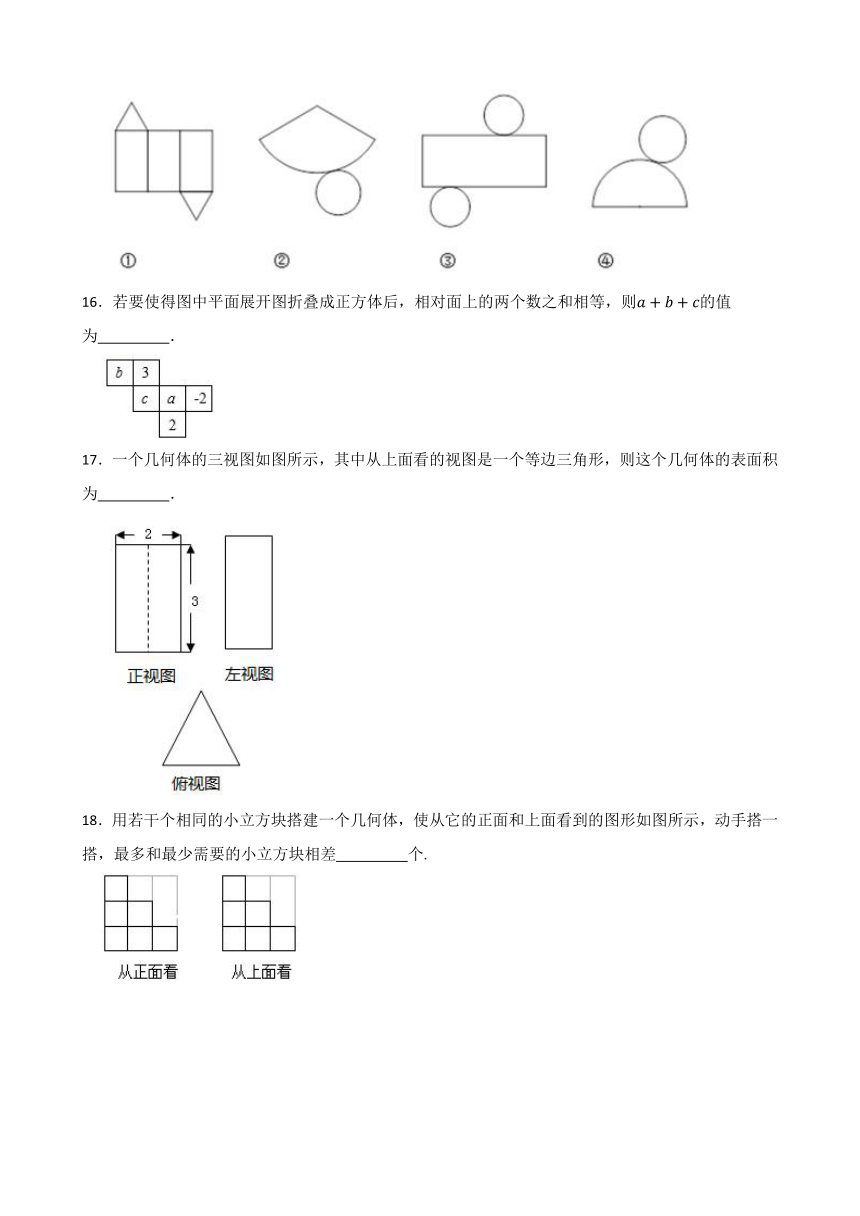
11.如图,圆锥的底面圆的半径是3,其母线长是9,则圆锥侧面展开图的扇形的圆心角度数是 °.
12.已知圆锥的底面半径为 ,母线长为 ,则它的侧面展开图的面积为 .
13.一个正方体盒子的展开图如图所示,如果要把它粘成一个正方体,那么与点A重合的点是点 .
14.如图,在△BOC中,∠COB=90°,OC=12,OB=5,将△BOC绕边OC所在直线旋转一周得到圆锥,则该圆锥的全面积是 .
15.下列几何体的展开图中,能围成圆锥的是 .
16.若要使得图中平面展开图折叠成正方体后,相对面上的两个数之和相等,则的值为 .
17.一个几何体的三视图如图所示,其中从上面看的视图是一个等边三角形,则这个几何体的表面积为 .
18.用若干个相同的小立方块搭建一个几何体,使从它的正面和上面看到的图形如图所示,动手搭一搭,最多和最少需要的小立方块相差 个.
三、解答题
19.如图,校园内有一棵与地面垂直的树,数学兴趣小组两次测量它在地面上的影子,第一次是阳光与地面成60°角时,第二次是阳光与地面成30°角时,两次测量的影长相差8米,求树高AB多少米.(结果保留根号)
20.如图,AB和DE是直立在地面上的两根立柱,已知AB=5m,同一时刻测量立柱AB在阳光下的投影BC=3m,立柱DE的投影DF=6m,请你计算立柱DE的长.(提示:光线AC与EF平行)
21.操场上有三根测杆AB,MN和XY,MN=XY,其中测杆AB在太阳光下某一时刻的影子为BC(如图中粗线).
(1)画出测杆MN在同一时刻的影子NP(用粗线表示),并简述画法;
(2)若在同一时刻测杆XY的影子的顶端恰好落在点B处,画出测杆XY所在的位置(用实线表示),并简述画法.
22.如图是一个几何体的三视图.
(1)写出这个几何体的名称;
(2)根据所示数据计算这个几何体的侧面积.
23.一个几何体的三视图如图所示(单位:mm),你能画出这个几何体的图形吗?并求出其表面积和体积.
24.如图1,一个边长为2cm的立方体按某种方式展开后,恰好能放在一个长方形内.
(1)计算图1长方形的面积;
(2)小明认为把该立方体按某种方式展开后可以放在如图2的长方形内,请你在图2中划出这个立方体的表面展开图;(图2每个小正方形边长为2cm);
(3)如图3,在长12cm、宽8cm的长方形内已经画出该立方体的一种表面展开图(各个面都用数字“1”表示),请你在剩下部分再画出2个该立方体的表面展开图,把一个立方体的每一个面标记为“2”,另一个立方体的每一个面标记为“3”.
答案解析部分
1.【答案】B
2.【答案】D
3.【答案】B
4.【答案】A
5.【答案】B
6.【答案】A
7.【答案】B
8.【答案】B
9.【答案】C
10.【答案】B
11.【答案】120
12.【答案】3πcm
13.【答案】D
14.【答案】90π
15.【答案】②④
16.【答案】12
17.【答案】
18.【答案】5
19.【答案】解:在Rt△ABD中,∵tan∠ADB= ,
∴BD= ,
在Rt△ACB中,∵tan∠ACB= ,
∴BC= ,
∵BC﹣BD=8,
∴ =8,
∴AB=4 (m).
答:树高AB为4 米
20.【答案】解:∵AC∥EF
∴∠ACB=EFD
又∵∠B=∠D=90°,
∴△ABC∽△ADF,
∴ ,
∴ ,
∴DE=10(m)
∴立柱DE的长为10m
21.【答案】解:(1)连接AC,过点M作MP∥AC交NC与P,
则NP为MN的影子;
(2)过B作BX∥AC,且BX=MP,过X作XY⊥NC交NC与Y,
则XY即为所求.
22.【答案】解:(1)由主视图和左视图为三角形判断出是锥体,由俯视图是圆形可判断出这个几何体应该是圆锥;
(2)根据三视图知:该圆锥的母线长为6,底面半径为2,
故侧面积=πrl=π×2×6=12π.
23.【答案】作图如下:
上下面积为16π×2=32π,左半面的侧面积是40π,右半面侧面积20π,还有中截面露出部分为40,所以表面积为:(92π+40) ,
体积:160π-40π=120πmm3.
24.【答案】(1)立方体的棱长为2cm,图1长方形的面积为4×2×3×2=48平方厘米。
(2)展开图:
(3)
一、单选题
1.将弧长为2πcm、圆心角为120°的扇形围成一个圆锥的侧面,则这个圆锥的高是( )
A. cm B.2 cm C.2cm D. cm
2.如图,该几何体的主视图是( )
A. B.
C. D.
3.如图,一个圆锥形漏斗的底面半径OA=5cm,高OC=12cm.则它的侧面积是( )
A.130cm2 B.65πcm2 C.60πcm2 D.30cm2
4.如图,是一个小正方体的展开图,把展开图折叠成小正方体后,有“三”字一面的相对面上的字是( )
A.高 B.同 C.创 D.安
5.下列几何体的三视图中,俯视图与主视图一定一致的是( )
A. B.
C. D.
6.奋进新时代,开启新征程.2021年12月28日12时,宁句城际正式开通,我市“一福地四名城”建设进一步推进.下列正方体的展开图上每个面上都有一个汉字.其中,“地”的对面是“名”的是( )
A. B.
C. D.
7.在某一时刻,测得一根高为1.8m的竹竿的影长为3m,同时测得一栋楼的影长为90m,则这栋楼的高度是( )
A.36m B.54m C.96m D.150m
8.如图,晚上小明在路灯下沿路从 处径直走到 处,这一过程中他在地上的影子( )
A.一直都在变短 B.先变短后变长
C.一直都在变长 D.先变长后变短
9.王华晚上由路灯 下的 处走到 处时,测得影子 的长为 ,继续往前走 到达 处时,测得影子 的长为 ,他的身高是 ,那么路灯 的高度 ( )
A. B. C. D.
10.某几何体由若干个大小相同的小正方体搭成,其主视图与左视图如图所示,则搭成这个几何体的小正方体最少有( )
A.3个 B.5个 C.7个 D.9个
二、填空题
11.如图,圆锥的底面圆的半径是3,其母线长是9,则圆锥侧面展开图的扇形的圆心角度数是 °.
12.已知圆锥的底面半径为 ,母线长为 ,则它的侧面展开图的面积为 .
13.一个正方体盒子的展开图如图所示,如果要把它粘成一个正方体,那么与点A重合的点是点 .
14.如图,在△BOC中,∠COB=90°,OC=12,OB=5,将△BOC绕边OC所在直线旋转一周得到圆锥,则该圆锥的全面积是 .
15.下列几何体的展开图中,能围成圆锥的是 .
16.若要使得图中平面展开图折叠成正方体后,相对面上的两个数之和相等,则的值为 .
17.一个几何体的三视图如图所示,其中从上面看的视图是一个等边三角形,则这个几何体的表面积为 .
18.用若干个相同的小立方块搭建一个几何体,使从它的正面和上面看到的图形如图所示,动手搭一搭,最多和最少需要的小立方块相差 个.
三、解答题
19.如图,校园内有一棵与地面垂直的树,数学兴趣小组两次测量它在地面上的影子,第一次是阳光与地面成60°角时,第二次是阳光与地面成30°角时,两次测量的影长相差8米,求树高AB多少米.(结果保留根号)
20.如图,AB和DE是直立在地面上的两根立柱,已知AB=5m,同一时刻测量立柱AB在阳光下的投影BC=3m,立柱DE的投影DF=6m,请你计算立柱DE的长.(提示:光线AC与EF平行)
21.操场上有三根测杆AB,MN和XY,MN=XY,其中测杆AB在太阳光下某一时刻的影子为BC(如图中粗线).
(1)画出测杆MN在同一时刻的影子NP(用粗线表示),并简述画法;
(2)若在同一时刻测杆XY的影子的顶端恰好落在点B处,画出测杆XY所在的位置(用实线表示),并简述画法.
22.如图是一个几何体的三视图.
(1)写出这个几何体的名称;
(2)根据所示数据计算这个几何体的侧面积.
23.一个几何体的三视图如图所示(单位:mm),你能画出这个几何体的图形吗?并求出其表面积和体积.
24.如图1,一个边长为2cm的立方体按某种方式展开后,恰好能放在一个长方形内.
(1)计算图1长方形的面积;
(2)小明认为把该立方体按某种方式展开后可以放在如图2的长方形内,请你在图2中划出这个立方体的表面展开图;(图2每个小正方形边长为2cm);
(3)如图3,在长12cm、宽8cm的长方形内已经画出该立方体的一种表面展开图(各个面都用数字“1”表示),请你在剩下部分再画出2个该立方体的表面展开图,把一个立方体的每一个面标记为“2”,另一个立方体的每一个面标记为“3”.
答案解析部分
1.【答案】B
2.【答案】D
3.【答案】B
4.【答案】A
5.【答案】B
6.【答案】A
7.【答案】B
8.【答案】B
9.【答案】C
10.【答案】B
11.【答案】120
12.【答案】3πcm
13.【答案】D
14.【答案】90π
15.【答案】②④
16.【答案】12
17.【答案】
18.【答案】5
19.【答案】解:在Rt△ABD中,∵tan∠ADB= ,
∴BD= ,
在Rt△ACB中,∵tan∠ACB= ,
∴BC= ,
∵BC﹣BD=8,
∴ =8,
∴AB=4 (m).
答:树高AB为4 米
20.【答案】解:∵AC∥EF
∴∠ACB=EFD
又∵∠B=∠D=90°,
∴△ABC∽△ADF,
∴ ,
∴ ,
∴DE=10(m)
∴立柱DE的长为10m
21.【答案】解:(1)连接AC,过点M作MP∥AC交NC与P,
则NP为MN的影子;
(2)过B作BX∥AC,且BX=MP,过X作XY⊥NC交NC与Y,
则XY即为所求.
22.【答案】解:(1)由主视图和左视图为三角形判断出是锥体,由俯视图是圆形可判断出这个几何体应该是圆锥;
(2)根据三视图知:该圆锥的母线长为6,底面半径为2,
故侧面积=πrl=π×2×6=12π.
23.【答案】作图如下:
上下面积为16π×2=32π,左半面的侧面积是40π,右半面侧面积20π,还有中截面露出部分为40,所以表面积为:(92π+40) ,
体积:160π-40π=120πmm3.
24.【答案】(1)立方体的棱长为2cm,图1长方形的面积为4×2×3×2=48平方厘米。
(2)展开图:
(3)
