5.3正方形 同步练习（含解析）

中小学教育资源及组卷应用平台
浙教版八年级下 5.3正方形同步练习
一．选择题
1．（2022 武功县模拟）如图，平行四边形ABCD中，对角线AC、BD相交于点O，则下列结论中不正确的是（　　）
A．当AB＝BC时，它是菱形 B．当AC⊥BD时，它是菱形
C．当AC＝BD时，它是矩形 D．当AC垂直平分BD时，它是正方形
2．（2022 虞城县二模）下列性质中，平行四边形，矩形，菱形，正方形共有的性质是（　　）
A．对角线相等 B．对角线互相垂直
C．对角线互相平分 D．对角线平分内角
3．（2021春 临沭县期中）正方形具有而矩形不一定具有的性质是（　　）
A．四个角为直角 B．对边平行且相等
C．对角线互相平分 D．对角线互相垂直
4．（2021春 路南区期中）已知正方形的对角线长为2，则此正方形的边长为（　　）
A． B．2 C． D．
5．（2021春 交城县期中）如图，点P是正方形ABCD的对角线BD上一点，PE⊥BC于点E，PF⊥CD于点F，连接AP，EF，下列结论中错误的是（　　）
A．AP＝EF B．∠PFE＝∠BAP
C．△APD一定是等腰三角形 D．AP⊥EF
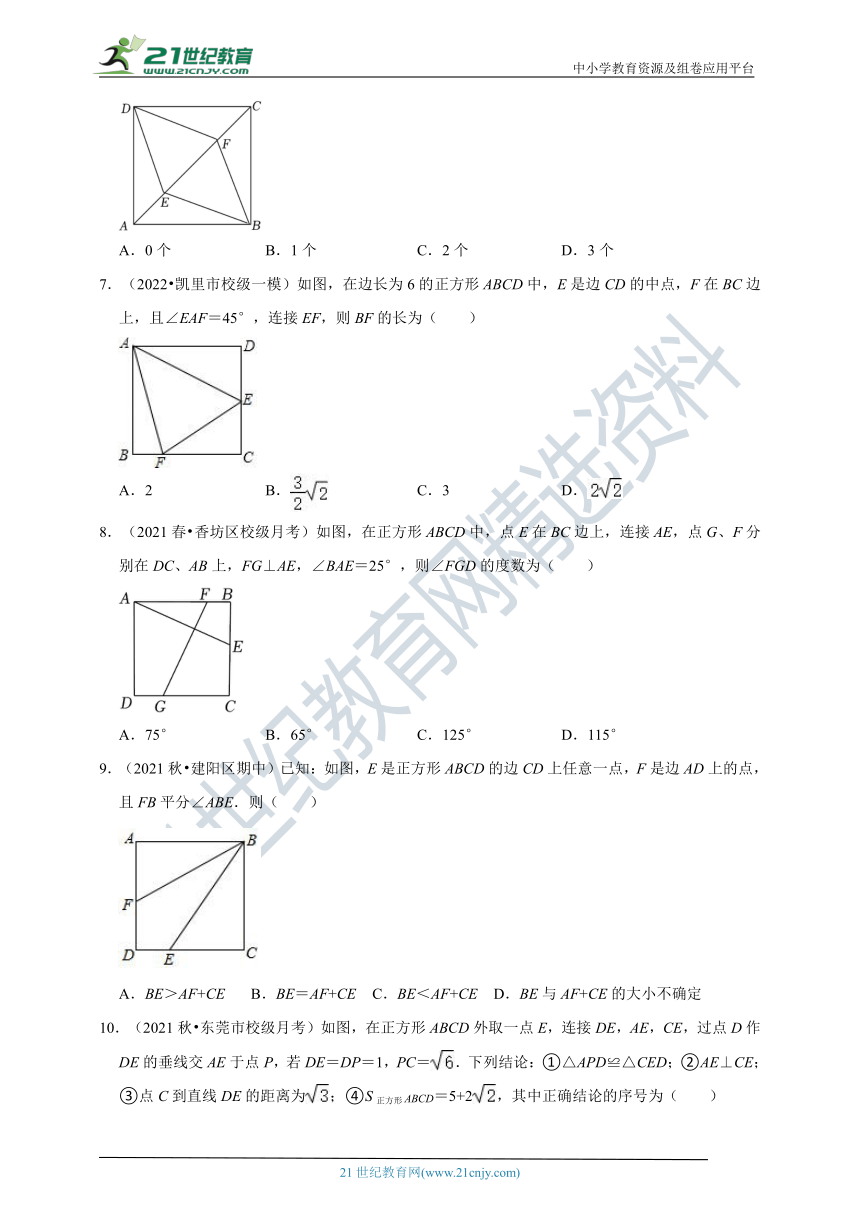
6．（2021春 曹县期中）如图，点E，F是正方形ABCD的对角线AC上两点，AE＝CF，连接DE，BE，DF，BF，下列结论：
（1）△ADE≌△ABE；（2）∠ABE＝∠CBF；（3）四边形DEBF是菱形；其中正确个数为（　　）
A．0个 B．1个 C．2个 D．3个
7．（2022 凯里市校级一模）如图，在边长为6的正方形ABCD中，E是边CD的中点，F在BC边上，且∠EAF＝45°，连接EF，则BF的长为（　　）
A．2 B． C．3 D．
8．（2021春 香坊区校级月考）如图，在正方形ABCD中，点E在BC边上，连接AE，点G、F分别在DC、AB上，FG⊥AE，∠BAE＝25°，则∠FGD的度数为（　　）
A．75° B．65° C．125° D．115°
9．（2021秋 建阳区期中）已知：如图，E是正方形ABCD的边CD上任意一点，F是边AD上的点，且FB平分∠ABE．则（　　）
A．BE＞AF+CE B．BE＝AF+CE C．BE＜AF+CE D．BE与AF+CE的大小不确定
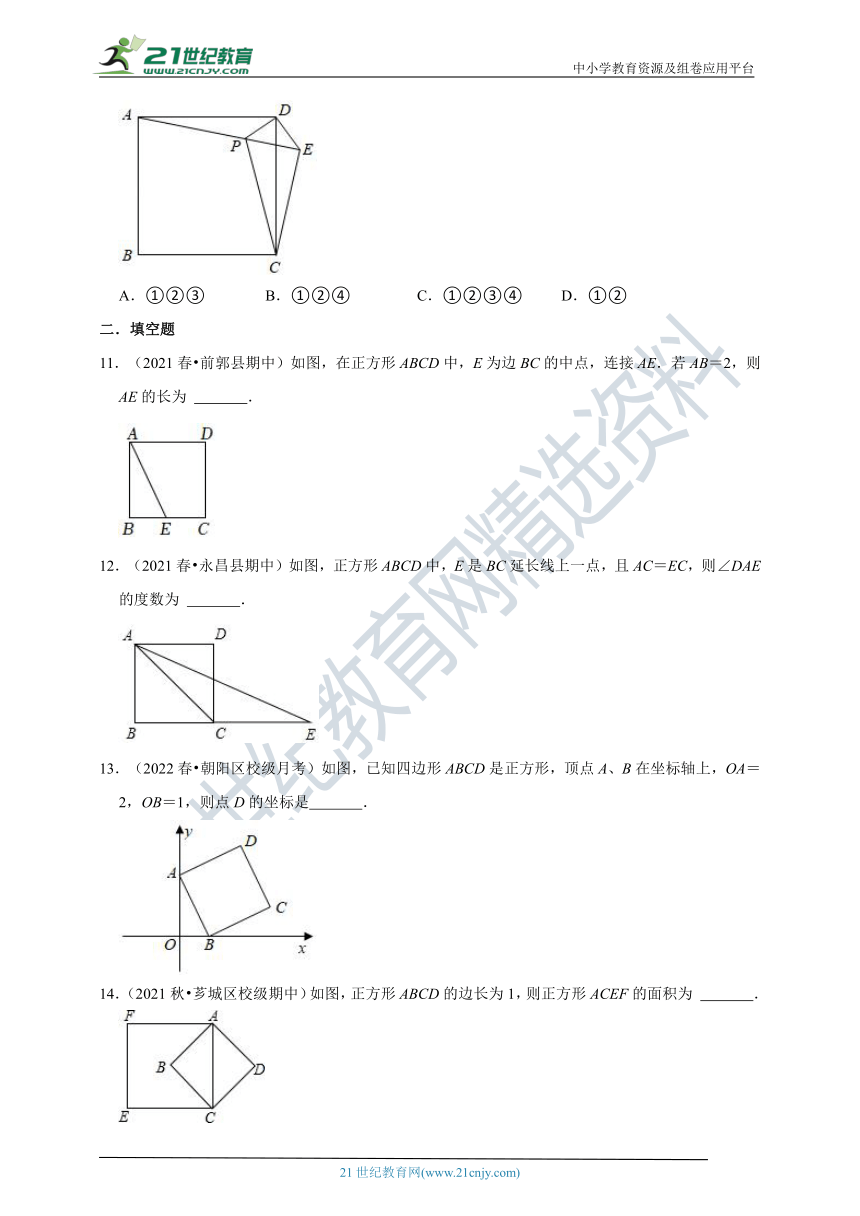
10．（2021秋 东莞市校级月考）如图，在正方形ABCD外取一点E，连接DE，AE，CE，过点D作DE的垂线交AE于点P，若DE＝DP＝1，PC＝．下列结论：①△APD≌△CED；②AE⊥CE；③点C到直线DE的距离为；④S正方形ABCD＝5+2，其中正确结论的序号为（　　）
A．①②③ B．①②④ C．①②③④ D．①②
二．填空题
11．（2021春 前郭县期中）如图，在正方形ABCD中，E为边BC的中点，连接AE．若AB＝2，则AE的长为 　 　．
12．（2021春 永昌县期中）如图，正方形ABCD中，E是BC延长线上一点，且AC＝EC，则∠DAE的度数为 　 　．
13．（2022春 朝阳区校级月考）如图，已知四边形ABCD是正方形，顶点A、B在坐标轴上，OA＝2，OB＝1，则点D的坐标是　 　．
14．（2021秋 芗城区校级期中）如图，正方形ABCD的边长为1，则正方形ACEF的面积为 　 　．
15．（2021春 德阳期末）如图，四边形ABCD是正方形，点G是边BC上一点，DE⊥AG于点E，BF∥DE，且交AG于点F．已知DE＝10，BF＝6，则EF的长度为 　 　．
16．（2021 恩平市模拟）如图，四边形ABCD是边长为a的正方形，点E是边BC上一动点（不与点B，C重合），∠AEF＝90°，且EF交正方形外角的平分线CF于点F，交CD于点G，连接AF．有下列结论：①AE＝EF；②CF＝BE；③∠DAF＝∠CFE；④△CEF面积的最大值为a2．其中正确的是 　 　．（把正确结论的序号都填上）
三．解答题
17．（2021秋 沈北新区期末）如图，边长为4的正方形ABCD，点E在AD边上，点F在CD边上，且AE＝2，DF＝1．
（1）求BE的长；
（2）请判断△BEF的形状，并说明理由．
18．（2021春 西峰区校级期中）如图，已知正方形ABCD的边长为，连接AC、BD交于点O，CE平分∠ACD交BD于点E，
（1）求DE的长；
（2）过点E作EF⊥CE，交AB于点F，求BF的长；
19．（2021秋 南岗区校级月考）如图1，正方形ABCD中，点E是边BC延长线上一点，连接DE，过点B作BF⊥DE，垂足为点F，BF与CD相交于点G．
（1）求证：△BCG≌△DCE；
（2）如图2，连接BD，若BE＝4，DG＝2，求BG的长．
20．（2021春 大洼区期中）如图，△ABC中，点O是边AC上一动点，过O作直线MN∥BC．设MN交∠ACB的平分线于点E，交∠ACB的外角平分线于点F．
（1）当点O在边AC上运动到什么位置时，四边形AECF为矩形？并说明理由；
（2）在（1）的条件下，△ABC满足什么条件时，四边形AECF是正方形？说明理由．
21．（2021秋 北镇市期中）如图，在正方形ABCD中，点E，F分别在AD，CD上，且AE＝DF，BE与AF相交于点O，P是BF的中点，连接OP．
（1）试判断AF与BE的关系，并证明你的结论；
（2）若AB＝5，AE＝2，求OP的长．
答案与解析
一．选择题
1．（2022 武功县模拟）如图，平行四边形ABCD中，对角线AC、BD相交于点O，则下列结论中不正确的是（　　）
A．当AB＝BC时，它是菱形 B．当AC⊥BD时，它是菱形
C．当AC＝BD时，它是矩形 D．当AC垂直平分BD时，它是正方形
【解析】解：∵四边形ABCD是平行四边形，
∴OA＝OC，OB＝OD，
当AB＝BC时，四边形ABCD是菱形，故A正确，
当AC⊥BD时，四边形ABCD是菱形，故B正确，
当AC＝BD时，四边形ABCD是矩形，故C正确，
当AC垂直平分BD时，它是正方形，故D不正确．
故选：D．
2．（2022 虞城县二模）下列性质中，平行四边形，矩形，菱形，正方形共有的性质是（　　）
A．对角线相等 B．对角线互相垂直
C．对角线互相平分 D．对角线平分内角
【解析】解：∵平行四边形的对角线互相平分，
∴矩形，菱形，正方形的对角线也必然互相平分．
故选：C．
3．（2021春 临沭县期中）正方形具有而矩形不一定具有的性质是（　　）
A．四个角为直角 B．对边平行且相等
C．对角线互相平分 D．对角线互相垂直
【解析】解：∵矩形的性质有四个角为直角，对边平行且相等，对角线互相平分且相等，正方形的性质有四个角为直角，对边平行且相等，对角线互相垂直平分且相等，
故选：D．
4．（2021春 路南区期中）已知正方形的对角线长为2，则此正方形的边长为（　　）
A． B．2 C． D．
【解析】解：如图：
由已知得：正方形ABCD中，BD＝2，
∴△ABD是等腰直角三角形，
∴AB＝AD＝BD＝，
故选：A．
5．（2021春 交城县期中）如图，点P是正方形ABCD的对角线BD上一点，PE⊥BC于点E，PF⊥CD于点F，连接AP，EF，下列结论中错误的是（　　）
A．AP＝EF B．∠PFE＝∠BAP
C．△APD一定是等腰三角形 D．AP⊥EF
【解析】解：连接PC，延长AP，FP交EF，AB于点G，H，如图，
∵正方形ABCD关于BD对称，
∴AP＝PC，∠BAP＝∠BCP，
∵PE⊥BC，PF⊥CD，∠BCD＝90°，
∴四边形PECF为矩形，
∴PC＝EF，∠FEC＝∠PCE＝∠PFE，PF＝CE，
∴AP＝EF，∠BAP＝∠PFE，故A、B选项不符合题意，
∵∠EPG+∠HPA＝∠HPA+∠BAP＝90°，
∴∠EPG＝∠BAP＝∠BCP＝∠FEC，
∵∠FEC+∠FEP＝90°，
∴∠EPG+∠GEP＝90°，
∴AP⊥EF，故D选项不符合题意，
故选：C．
6．（2021春 曹县期中）如图，点E，F是正方形ABCD的对角线AC上两点，AE＝CF，连接DE，BE，DF，BF，下列结论：
（1）△ADE≌△ABE；（2）∠ABE＝∠CBF；（3）四边形DEBF是菱形；其中正确个数为（　　）
A．0个 B．1个 C．2个 D．3个
【解析】解：∵四边形ABCD是正方形，
∴AD＝AB，∠DAE＝∠BAE＝45°，
在△ADE与△ABE中，
，
∴△ADE≌△ABE；故（1）正确；
连接BD交AC于O，
∴AO＝CO，DO＝BO，BD⊥AC，
∴四边形DEBF是菱形，故（3）正确；
∴∠EBO＝∠FBO，
∵∠ABO＝∠CBO＝45°，
∴∠ABE＝∠CBF，故（2）正确；
故选：D．
7．（2022 凯里市校级一模）如图，在边长为6的正方形ABCD中，E是边CD的中点，F在BC边上，且∠EAF＝45°，连接EF，则BF的长为（　　）
A．2 B． C．3 D．
【解析】证明：∵四边形ABCD是正方形，
∴AB＝AD，
∴把△ABF绕点A逆时针旋转90°至△ADG，可使AB与AD重合，如图：
∴∠BAF＝∠DAG，
∵∠BAD＝90°，∠EAF＝45°，
∴∠BAF+∠DAE＝45°，
∴∠EAF＝∠EAG，
∵∠ADG＝∠ADC＝∠B＝90°，
∴∠EDG＝180°，点E、D、G共线，
在△AFE和△AGE中，
，
∴△AFE≌△AGE（SAS），
∴EF＝EG，
即：EF＝EG＝ED+DG，
∵E为CD的中点，边长为6的正方形ABCD，
∴CD＝BC＝6，DE＝CE＝3，∠C＝90°，
∴设BF＝x，则CF＝6﹣x，EF＝3+x，
在Rt△CFE中，由勾股定理得：
EF2＝CE2+CF2，
∴（3+x）2＝32+（6﹣x）2，
解得：x＝2，
即BF＝2，
故选：A．
8．（2021春 香坊区校级月考）如图，在正方形ABCD中，点E在BC边上，连接AE，点G、F分别在DC、AB上，FG⊥AE，∠BAE＝25°，则∠FGD的度数为（　　）
A．75° B．65° C．125° D．115°
【解析】解：过F作FH⊥CD于H，交AE于G，
∵四边形ABCD是正方形，
∴∠B＝∠BAD＝90°，AB∥CD，
∴FH⊥AB，
∴∠AFG＝90°，
∵∠AGF＝90°，
∴∠BAE＝∠HFG＝90°﹣∠AGF，＝25°，
∴FGD＝∠FHG+∠HFG＝90°+25°＝115°，
故选：D．
方法二：∵FG⊥AE，
∴∠AGF＝90°，
∵∠BAE＝25°，
∴∠AFG＝90°﹣∠BAE＝90°﹣25°＝65°，
∵四边形ABCD是正方形，
∴AB∥CD，
∴∠FDG+∠AFG＝180°，
∴∠FDG＝180°﹣∠AFG＝180°﹣65°＝115°，
故选：D．
9．（2021秋 建阳区期中）已知：如图，E是正方形ABCD的边CD上任意一点，F是边AD上的点，且FB平分∠ABE．则（　　）
A．BE＞AF+CE B．BE＝AF+CE C．BE＜AF+CE D．BE与AF+CE的大小不确定
【解析】证明：如图，延长DC到G，使CG＝AF，连接BG，
∵四边形ABCD是正方形，
∴AB＝BC，∠A＝∠BCG＝90°，
在△ABF和△CBG中，
，
∴△ABF≌△CBG（SAS），
∴∠AFB＝∠G，∠ABF＝∠CBG，
∵∠ABF＝∠EBF，
∴∠EBF＝∠CBG，
∴∠EBF+∠CBE＝∠CBG+∠CBE，
即∠FBC＝∠EBG，
∵AD∥BC，
∴∠AFB＝∠FBC＝∠EBG，
∴∠EBG＝∠G，
∴BE＝EG＝CG+CE＝AF+CE．
故选：B．
10．（2021秋 东莞市校级月考）如图，在正方形ABCD外取一点E，连接DE，AE，CE，过点D作DE的垂线交AE于点P，若DE＝DP＝1，PC＝．下列结论：①△APD≌△CED；②AE⊥CE；③点C到直线DE的距离为；④S正方形ABCD＝5+2，其中正确结论的序号为（　　）
A．①②③ B．①②④ C．①②③④ D．①②
【解析】解：①∵DP⊥DE，
∴∠PDE＝90°．
∴∠PDC+∠CDE＝90°，
∵在正方形ABCD中，∠ADC＝∠ADP+∠PDC＝90°，AD＝CD，
∴∠CDE＝∠ADP．
在△APD和△CED中，
，
∴△APD≌△CED（SAS），
故①正确；
②∵△APD≌△CED，
∴∠APD＝∠CED，
又∵∠APD＝∠PDE+∠DEP，∠CED＝∠CEA+∠DEP，
∴∠PDE＝∠CEA＝90°．
即AE⊥CE，故②正确；
③过点C作CF⊥DE的延长线于点F，如图，
∵DE＝DP，∠PDE＝90°，
∴∠DPE＝∠DEP＝45°．
又∵∠CEA＝90°，
∴∠CEF＝∠FCE＝45°．
∵DP＝DE＝1，
∴PE＝＝＝．
∴CE＝＝＝2，
∴CF＝EF＝CE＝，
即点C到直线DE的距离为，故③错误；
④∵CF＝EF＝，DE＝1，
在Rt△CDF中，CD2＝CF2+DF2＝（）2+（1+）2＝2+3+2＝5+2，
∴S正方形ABCD＝5+2，
故④正确．
综上所述，正确结论的序号为①②④，
故选：B．
二．填空题
11．（2021春 前郭县期中）如图，在正方形ABCD中，E为边BC的中点，连接AE．若AB＝2，则AE的长为 　　．
【解析】解：在正方形ABCD中，AB＝BC＝2，∠B＝90°，
∵E为BC中点，
∴BE＝CE＝1，
∴AE＝＝，
故答案为：．
12．（2021春 永昌县期中）如图，正方形ABCD中，E是BC延长线上一点，且AC＝EC，则∠DAE的度数为 　22.5°　．
【解析】解：∵四边形ABCD为正方形，
∴∠DAC＝∠ACB＝45°，
∵AC＝CE，
∴∠E＝∠EAC，
∵2∠EAC＝∠E+∠EAC＝∠ACB＝45°，
∴∠EAC＝22.5°，
∴∠DAE＝∠DAC﹣∠EAC＝45°﹣22.5°＝22.5°．
故答案为：22.5°．
13．（2022春 朝阳区校级月考）如图，已知四边形ABCD是正方形，顶点A、B在坐标轴上，OA＝2，OB＝1，则点D的坐标是　（2，3）　．
【解析】解：作DE垂直于y轴于点E，
∵∠DAB＝90°，DE⊥y轴，
∴∠DAE+∠EDA＝90°，∠DAE+∠BAO＝90°，
又∵∠AOB＝90°，AD＝AB，
∴△DAE≌△ABO（AAS），
∴AE＝BO＝1，DE＝AO＝2，
∴OE＝AO+AE＝3，
即点D的坐标为（2，3）．
故答案为：（2，3）．
14．（2021秋 芗城区校级期中）如图，正方形ABCD的边长为1，则正方形ACEF的面积为 　2　．
【解析】解：由勾股定理，得AC＝＝＝，
乘方，得（）2＝2，
故答案为：2．
15．（2021春 德阳期末）如图，四边形ABCD是正方形，点G是边BC上一点，DE⊥AG于点E，BF∥DE，且交AG于点F．已知DE＝10，BF＝6，则EF的长度为 　4　．
【解析】解：∵四边形ABCD是正方形，
∴AB＝AD，∠BAF+∠DAE＝∠BAD＝90°，
又∵DE⊥AG，BF∥DE，
∴∠AED＝∠BFA＝90°，
∵∠BAF+∠ABF＝90°，
∴∠ABF＝∠DAE，
在△ABF和△DAE中，
，
∴△DAE≌△ABF（AAS），
∴AE＝BF，AF＝DE，
∴EF＝AF﹣AE＝DE﹣BF＝10﹣6＝4．
故答案为：4．
16．（2021 恩平市模拟）如图，四边形ABCD是边长为a的正方形，点E是边BC上一动点（不与点B，C重合），∠AEF＝90°，且EF交正方形外角的平分线CF于点F，交CD于点G，连接AF．有下列结论：①AE＝EF；②CF＝BE；③∠DAF＝∠CFE；④△CEF面积的最大值为a2．其中正确的是 　①②③　．（把正确结论的序号都填上）
【解析】解：在AB上取点H，使AH＝EC，连接EH，
∵∠HAE+∠AEB＝90°，∠CEF+∠AEB＝90°，
∴∠HAE＝∠CEF，
又∵AH＝CE，
∴BH＝BE，
∴∠AHE＝135°，
∵CF是正方形外角的平分线，
∴∠ECF＝135°，
∴∠AHE＝∠ECF，
在△AHE和△ECF中，
，
∴△AHE≌△ECF（ASA），
∴AE＝EF，AH＝CF，
∴①说法符合题意，
∵BE＝BH，
∴EH＝BE，
∴CF＝BE，
∴②说法符合题意，
∵∠AHE＝135°，
∴∠HAE+∠AEH＝45°，
又∵AE＝EF，
∴∠EAF＝45°，
∴∠HAE+∠DAF＝45°，
∴∠AEH＝∠DAF，
∵∠AEH＝∠EFC，
∴∠DAF＝∠EFC，
∴③说法符合题意，
∵△AHE≌△ECF，
∴S△AHE＝S△CEF，
设AH＝x，则，
当x＝时，S△AHE取最大值为，
∴④说法不合题意，
故答案为①②③．
三．解答题
17．（2021秋 沈北新区期末）如图，边长为4的正方形ABCD，点E在AD边上，点F在CD边上，且AE＝2，DF＝1．
（1）求BE的长；
（2）请判断△BEF的形状，并说明理由．
【解析】解：（1）∵四边形ABCD是正方形，
∴AB＝AD＝CD＝BC＝4，∠A＝∠D＝∠C＝90°，
∴BE＝＝＝2；
（2）△BEF是直角三角形，理由如下：
∵AE＝2，DF＝1，
∴DE＝2，FC＝3，
∴EF＝＝＝，BF＝＝＝5，
∴EF2+BE2＝25＝BF2，
∴∠BEF＝90°，即△BEF是直角三角形．
18．（2021春 西峰区校级期中）如图，已知正方形ABCD的边长为，连接AC、BD交于点O，CE平分∠ACD交BD于点E，
（1）求DE的长；
（2）过点E作EF⊥CE，交AB于点F，求BF的长；
【解析】解：（1）∵四边形ABCD是正方形，
∴∠ABC＝∠ADC＝90°，
∠DBC＝∠BCA＝∠ACD＝45°，
∵CE平分∠DCA，
∴∠ACE＝∠DCE＝∠ACD＝22.5°，
∴∠BCE＝∠BCA+∠ACE＝45°+22.5°＝67.5°，
∵∠DBC＝45°，
∴∠BEC＝180°﹣67.5°﹣45°＝67.5°＝∠BCE，
∴BE＝BC＝2，
在Rt△BCD中，由勾股定理得：BD＝，
∴DE＝BD﹣BE＝2﹣2；
（2）∵FE⊥CE，
∴∠CEF＝90°，
∴∠FEB＝∠CEF﹣∠CEB＝90°﹣67.5°＝22.5°＝∠DCE，
在△BEF和△DCE中，
∴△FEB≌△ECD（ASA），
∴BF＝DE＝2﹣2．
19．（2021秋 南岗区校级月考）如图1，正方形ABCD中，点E是边BC延长线上一点，连接DE，过点B作BF⊥DE，垂足为点F，BF与CD相交于点G．
（1）求证：△BCG≌△DCE；
（2）如图2，连接BD，若BE＝4，DG＝2，求BG的长．
【解析】（1）证明：∵四边形ABCD是正方形，
∴∠BCG＝∠DCE＝90°，BC＝CD，
∵BF⊥DE，
∴∠DFG＝∠BCG＝90°，
∵∠BGC＝∠DGF，
∴∠CBG＝∠CDE．
在△BCG和△DCE中，
，
∴△BCG≌△DCE（SAS）；
（2）解：由（1）得出△BCG≌△DCE，
∴CG＝CE，
又∵BE＝BC+CE＝4，DG＝CD﹣CG＝2，
∴BC＝3，CG＝，
在Rt△BCG中，BG＝．
20．（2021春 大洼区期中）如图，△ABC中，点O是边AC上一动点，过O作直线MN∥BC．设MN交∠ACB的平分线于点E，交∠ACB的外角平分线于点F．
（1）当点O在边AC上运动到什么位置时，四边形AECF为矩形？并说明理由；
（2）在（1）的条件下，△ABC满足什么条件时，四边形AECF是正方形？说明理由．
【解析】解：（1）当点O运动到AC边的中点时，四边形AECF是矩形．
理由：∵MN交∠ACB的平分线于点E，交∠ACB的外角平分线于点F．
∴∠ACE＝∠BCE＝∠ACB，
∴∠ACF＝∠DCF∠ACD，
∵EF∥BC，
∴∠FEC＝∠BCE，
∴∠EFC＝∠DCF，
∴∠ACE＝∠FEC，∠ACF＝∠EFC，
∴OE＝OC，OF＝OC，
∴OE＝OF，
当点O运动到AC边的中点时，OA＝OC，
∴四边形AECF为平行四边形，
又∵∠ACE+∠ACF＝∠ACB+∠ACD＝90°，
∴四边形AECF为矩形；
（2）当△ABC为直角三角形，∠ACB＝90°时，四边形AECF是正方形，
理由：∵∠ACB＝90°，
∴AC⊥BC，
∵EF∥BC，
∴AC⊥EF，
∵四边形AECF为矩形，
∴四边形AECF是正方形．
21．（2021秋 北镇市期中）如图，在正方形ABCD中，点E，F分别在AD，CD上，且AE＝DF，BE与AF相交于点O，P是BF的中点，连接OP．
（1）试判断AF与BE的关系，并证明你的结论；
（2）若AB＝5，AE＝2，求OP的长．
【解析】解：（1）AF＝BE，且AF⊥BE，理由如下：
∵四边形ABCD是正方形，
∴AB＝AD，∠BAD＝∠ADC＝90°，
在△BAE和△ADF中，
，
∴△BAE≌△ADF（SAS），
∴AF＝BE，∠DAF＝∠ABE，
∵∠ABE+∠BEA＝90°，
∴∠DAF+∠BEA＝90°，
∴AF⊥BE；
（2）由（1）知∴△BAE≌△ADF，
∴∠ABE＝∠DAF，
∵∠ABE+∠BEA＝90°，
∴∠DAF+∠BEA＝90°，
∴∠AOE＝∠BOF＝90°，
∵点P为BF的中点，
∴OP＝BF，
∵BC＝AB＝CD＝5，AE＝DF＝2，
∴CF＝CD﹣DF＝5﹣2＝3，
∴BF＝＝＝，
∴OP＝．
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 （共 2 页）
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)