5.2平行四边形同步测控及答案
图片预览

文档简介
5. 2 平行四边形
【要点预习】
1. 平行四边形的概念:
两组对边 的四边形叫做平行四边形.
2. 平行四边形的性质:
平行四边形的 相等.
【课前热身】
1. 在□ABCD中,若∠A=60°,则∠B= .
答案:120°
2. 在□ABCD中,若∠A+∠C=160°,则∠D= .
答案:100°
3. 在□ABCD中,∠A:∠B=2:3,则∠B=_____.
答案:108°
4. 可伸缩的栅栏门运用了平行四边形的性质: .
答案:不稳定性
【讲练互动】
【例1】如图,在□ABCD中,DB=CD,∠C=70°,AE⊥BD于点E,求∠DAE的度数.
解:∵DB=CD,∴∠DBC=∠C=70°.
∵四边形ABCD是平行四边形,∴AD∥BC,∴∠ADB=∠DBC=70°.
∵AE⊥BD,∴∠AED=90°,∴∠DAE=20°.
【变式训练】
1. 如图所示,在□ABCD中,DE⊥AB于E,DF⊥BC于F,若∠A=55°,求∠EDF的度数.
解:∵四边形ABCD是平行四边形,∴AD∥BC,∴∠A+∠B=180°. ∵∠A=55°,∴∠B=125°.
∵DE⊥AB,DF⊥BC,∴∠DEB=∠DFB=90°.
∵∠EDF+∠DEB+∠B+∠DFB=360°,∴∠EDF=55°.
【例2】如图,在□ABCD中,AE与CF分别平分∠BAD与∠DCB. 求证:四边形AECF是平行四边形.
分析:要证四边形AECF是平行四边形,根据定义只能证AF∥EC且AE∥FC,前者显然已知,为此只需证∠AEB=∠FCE,即需证它们都与∠DFC相等.
证明:∵四边形ABCD是平行四边形,∴∠B=∠D,∠BAD=∠DCB.
∵AE与CF分别平分∠BAD与∠DCB,∴∠BAE=∠BAD=∠DCB=∠DCF.
∴∠AEB=∠CFD.
∵AD∥BC,∴∠CFD=∠FCB,∴∠BEA=∠FCB,
∴AE∥FC,∴四边形AECF是平行四边形.
【绿色通道】要证四边形是平行四边形目前唯一的方法是证明两组对边分别平行.
【变式训练】
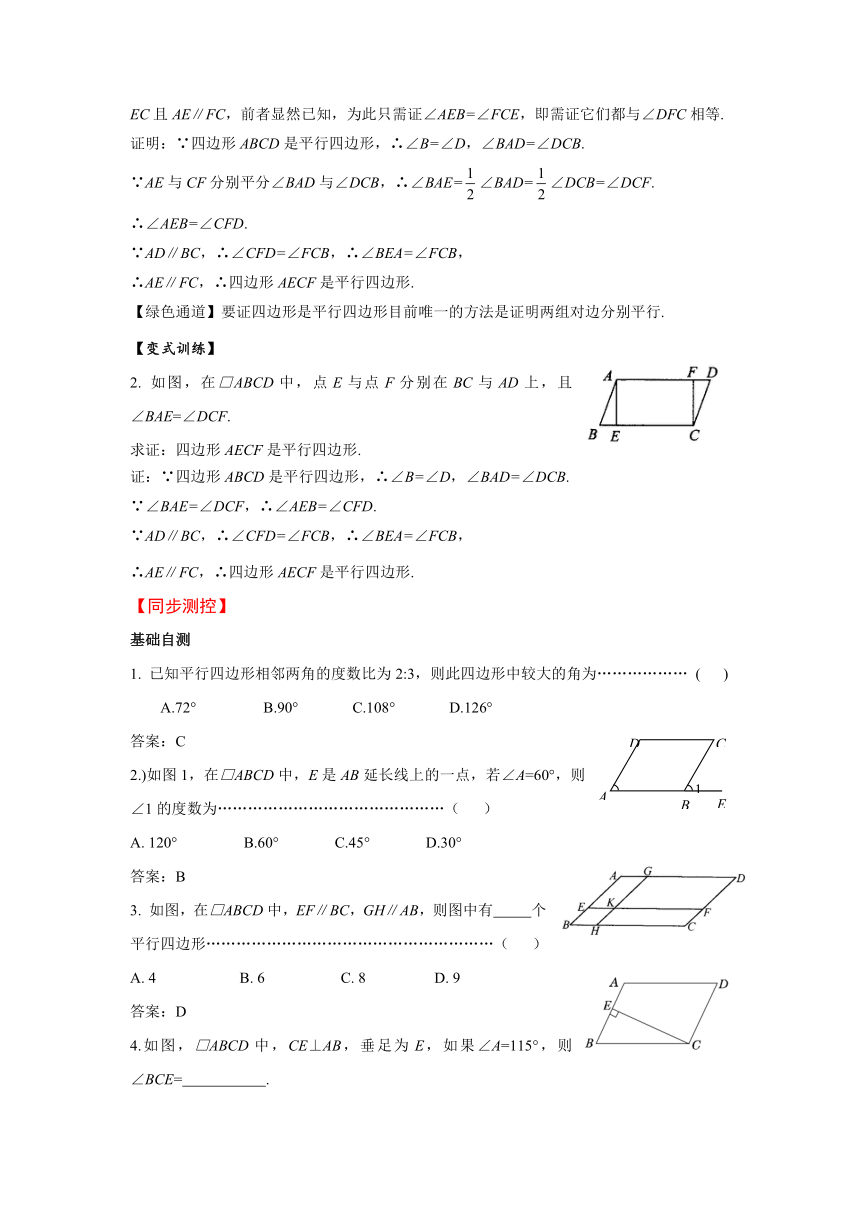
2. 如图,在□ABCD中,点E与点F分别在BC与AD上,且∠BAE=∠DCF.
求证:四边形AECF是平行四边形.
证:∵四边形ABCD是平行四边形,∴∠B=∠D,∠BAD=∠DCB.
∵∠BAE=∠DCF,∴∠AEB=∠CFD.
∵AD∥BC,∴∠CFD=∠FCB,∴∠BEA=∠FCB,
∴AE∥FC,∴四边形AECF是平行四边形.
【同步测控】
基础自测
1. 已知平行四边形相邻两角的度数比为2:3,则此四边形中较大的角为……………… ( )
A.72° B.90° C.108° D.126°
答案:C
2.)如图1,在□ABCD中,E是AB延长线上的一点,若∠A=60°,则∠1的度数为………………………………………( )
A. 120° B.60° C.45° D.30°
答案:B
3. 如图,在□ABCD中,EF∥BC,GH∥AB,则图中有 个平行四边形…………………………………………………( )
A. 4 B. 6 C. 8 D. 9
答案:D
4.如图,□ABCD中,CE⊥AB,垂足为E,如果∠A=115°,则∠BCE= .
答案:25°
5. 在□ABCD中,∠ABC的平分线与∠BCD的平分线相交于点O,则∠BOC的度数为 .
答案:90°
6. 如图,在□ABCD中,AD=5,AB=3,BE平分∠ABC,则DE= .
答案:2
7. 在□ABCD中,AB=3,BC=5,AC=4,则□ABCD的面积等于_______.
答案:12
8. 已知:∠α和线段a、b.
求作:□ABCD,使∠A=∠α,AB=a,AD=b
作法:(1)作∠EAF=∠α;
(2)在AE上截取AD=b,AB=a;
(3)过D作DC∥AB,过B作BC∥AD.
∴四边形ABCD就是所求的平行四边形.
9.如图,已知□ABCD中,点E为BC边的中点,延长DE,AB相交于点F. 求证:CD=BF.
证明:∵四边形ABCD是平行四边形,∴DC∥AB,
∴∠C=∠CBF,∠CDF=∠F.
∵点E为BC边的中点,∴CE=BE.
∴△CDE≌△BEF(AAS),∴CD=BF.
能力提升
10.如图,在□ABCD中,DE是∠ADC的平分线,F是AB的中点,AB=6,AD=4,则AE:EF:BE为………( )
A. 4:1:2 B. 4:1:3 C. 3:1:2 D. 5:1:2
解析:由已知得DC∥AB,得∠CDE=∠DEA,而∠CDE=∠ADE,于是可得∠ADE=∠AED,即得AE=AD=4,又AB=6,故BE=2,AF=3,EF=1.
答案:A
11.如图,将一平行四边形纸片ABCD沿AE,EF折叠,使点E,B,C在同一直线上,则∠AEF= .
解析:由题意知△AEB≌△AEB′,△CEF≌△C′EF,于是得∠AEB=∠AEB′,∠CEF=∠C′EF,故∠AEF=90°.
答案:90°
12. 如图,平行四边形纸条ABCD中,E、F分别是边AD、BC的中点. 张老师请同学们将纸条的下半部分平行四边形ABEF沿EF翻折得平行四边形A1B1FE,得到一个V字形图案.若∠A=63°,则∠B1FC= 度.
解析:如图是翻折后的图形,由已知易得∠B1FE=∠BFE=∠A=63°,于是得∠B1FC=180°-2×63°=54°.
答案:54
13. 如图所示,在□ABCD中,点E,F分别在BC,AD上,AE∥CF,求证:∠AFC=∠AEC.
证明:∵四边形ABCD是平行四边形,∴AD∥BC,
又∵AE∥CF,∴四边形AECF是平行四边形,∴∠AFC=∠AEC.
14. 已知:△ABC与□DEFG如图放置,点D,G分别在边AB,AC上,点E,F在边BC上. 已知BE=DE,CF=FG,求∠A的度数.
解:∵BE=DE,∴∠B=∠EDB,∴∠DEF=2∠B.
∵CF=FG,∴∠C=∠FGC,∴∠GFE=2∠C.
∵四边形DEFG是平行四边形,∴DE∥FG,∴∠DEF+∠GFE=180°,
∴2(∠B+∠C)=180°,即∠B+∠C=90°,∴∠A=90°.
创新应用
15. 如图,点A,B,D分别是△EFC中EF,FC,EC边上的三点,若四边形ABCD是平行四边形,且∠EAD=∠FAB.
(1)请找出图中所有的等腰三角形,并说明理由.
(2)若CF=5,求□ABCD的周长.
分析:要找等腰三角形,只需找图中相等的角,这可结合平行线的性质和已知条件推得;结合题设和等腰三角形的腰长相等便可求得平行四边形的周长.
解:(1)△DAE,△BAF,△CEF都是等腰三角形.
∵四边形ABCD是平行四边形,∴AD∥BC,AB∥CD,
∴∠EAD=∠F,∠FAB=∠E.
∵∠EAD=∠FAB,∴∠EAD=∠F=∠FAB=∠E,
∴△DAE,△BAF,△CEF都是等腰三角形.
(2)∵△DAE,△BAF和△CEF都是等腰三角形,∴AD=DE,AB=BF,CE=CF=5.
∴AB+BC=CD+AD=5,即□ABCD的周长=5+5=10.
【要点预习】
1. 平行四边形的概念:
两组对边 的四边形叫做平行四边形.
2. 平行四边形的性质:
平行四边形的 相等.
【课前热身】
1. 在□ABCD中,若∠A=60°,则∠B= .
答案:120°
2. 在□ABCD中,若∠A+∠C=160°,则∠D= .
答案:100°
3. 在□ABCD中,∠A:∠B=2:3,则∠B=_____.
答案:108°
4. 可伸缩的栅栏门运用了平行四边形的性质: .
答案:不稳定性
【讲练互动】
【例1】如图,在□ABCD中,DB=CD,∠C=70°,AE⊥BD于点E,求∠DAE的度数.
解:∵DB=CD,∴∠DBC=∠C=70°.
∵四边形ABCD是平行四边形,∴AD∥BC,∴∠ADB=∠DBC=70°.
∵AE⊥BD,∴∠AED=90°,∴∠DAE=20°.
【变式训练】
1. 如图所示,在□ABCD中,DE⊥AB于E,DF⊥BC于F,若∠A=55°,求∠EDF的度数.
解:∵四边形ABCD是平行四边形,∴AD∥BC,∴∠A+∠B=180°. ∵∠A=55°,∴∠B=125°.
∵DE⊥AB,DF⊥BC,∴∠DEB=∠DFB=90°.
∵∠EDF+∠DEB+∠B+∠DFB=360°,∴∠EDF=55°.
【例2】如图,在□ABCD中,AE与CF分别平分∠BAD与∠DCB. 求证:四边形AECF是平行四边形.
分析:要证四边形AECF是平行四边形,根据定义只能证AF∥EC且AE∥FC,前者显然已知,为此只需证∠AEB=∠FCE,即需证它们都与∠DFC相等.
证明:∵四边形ABCD是平行四边形,∴∠B=∠D,∠BAD=∠DCB.
∵AE与CF分别平分∠BAD与∠DCB,∴∠BAE=∠BAD=∠DCB=∠DCF.
∴∠AEB=∠CFD.
∵AD∥BC,∴∠CFD=∠FCB,∴∠BEA=∠FCB,
∴AE∥FC,∴四边形AECF是平行四边形.
【绿色通道】要证四边形是平行四边形目前唯一的方法是证明两组对边分别平行.
【变式训练】
2. 如图,在□ABCD中,点E与点F分别在BC与AD上,且∠BAE=∠DCF.
求证:四边形AECF是平行四边形.
证:∵四边形ABCD是平行四边形,∴∠B=∠D,∠BAD=∠DCB.
∵∠BAE=∠DCF,∴∠AEB=∠CFD.
∵AD∥BC,∴∠CFD=∠FCB,∴∠BEA=∠FCB,
∴AE∥FC,∴四边形AECF是平行四边形.
【同步测控】
基础自测
1. 已知平行四边形相邻两角的度数比为2:3,则此四边形中较大的角为……………… ( )
A.72° B.90° C.108° D.126°
答案:C
2.)如图1,在□ABCD中,E是AB延长线上的一点,若∠A=60°,则∠1的度数为………………………………………( )
A. 120° B.60° C.45° D.30°
答案:B
3. 如图,在□ABCD中,EF∥BC,GH∥AB,则图中有 个平行四边形…………………………………………………( )
A. 4 B. 6 C. 8 D. 9
答案:D
4.如图,□ABCD中,CE⊥AB,垂足为E,如果∠A=115°,则∠BCE= .
答案:25°
5. 在□ABCD中,∠ABC的平分线与∠BCD的平分线相交于点O,则∠BOC的度数为 .
答案:90°
6. 如图,在□ABCD中,AD=5,AB=3,BE平分∠ABC,则DE= .
答案:2
7. 在□ABCD中,AB=3,BC=5,AC=4,则□ABCD的面积等于_______.
答案:12
8. 已知:∠α和线段a、b.
求作:□ABCD,使∠A=∠α,AB=a,AD=b
作法:(1)作∠EAF=∠α;
(2)在AE上截取AD=b,AB=a;
(3)过D作DC∥AB,过B作BC∥AD.
∴四边形ABCD就是所求的平行四边形.
9.如图,已知□ABCD中,点E为BC边的中点,延长DE,AB相交于点F. 求证:CD=BF.
证明:∵四边形ABCD是平行四边形,∴DC∥AB,
∴∠C=∠CBF,∠CDF=∠F.
∵点E为BC边的中点,∴CE=BE.
∴△CDE≌△BEF(AAS),∴CD=BF.
能力提升
10.如图,在□ABCD中,DE是∠ADC的平分线,F是AB的中点,AB=6,AD=4,则AE:EF:BE为………( )
A. 4:1:2 B. 4:1:3 C. 3:1:2 D. 5:1:2
解析:由已知得DC∥AB,得∠CDE=∠DEA,而∠CDE=∠ADE,于是可得∠ADE=∠AED,即得AE=AD=4,又AB=6,故BE=2,AF=3,EF=1.
答案:A
11.如图,将一平行四边形纸片ABCD沿AE,EF折叠,使点E,B,C在同一直线上,则∠AEF= .
解析:由题意知△AEB≌△AEB′,△CEF≌△C′EF,于是得∠AEB=∠AEB′,∠CEF=∠C′EF,故∠AEF=90°.
答案:90°
12. 如图,平行四边形纸条ABCD中,E、F分别是边AD、BC的中点. 张老师请同学们将纸条的下半部分平行四边形ABEF沿EF翻折得平行四边形A1B1FE,得到一个V字形图案.若∠A=63°,则∠B1FC= 度.
解析:如图是翻折后的图形,由已知易得∠B1FE=∠BFE=∠A=63°,于是得∠B1FC=180°-2×63°=54°.
答案:54
13. 如图所示,在□ABCD中,点E,F分别在BC,AD上,AE∥CF,求证:∠AFC=∠AEC.
证明:∵四边形ABCD是平行四边形,∴AD∥BC,
又∵AE∥CF,∴四边形AECF是平行四边形,∴∠AFC=∠AEC.
14. 已知:△ABC与□DEFG如图放置,点D,G分别在边AB,AC上,点E,F在边BC上. 已知BE=DE,CF=FG,求∠A的度数.
解:∵BE=DE,∴∠B=∠EDB,∴∠DEF=2∠B.
∵CF=FG,∴∠C=∠FGC,∴∠GFE=2∠C.
∵四边形DEFG是平行四边形,∴DE∥FG,∴∠DEF+∠GFE=180°,
∴2(∠B+∠C)=180°,即∠B+∠C=90°,∴∠A=90°.
创新应用
15. 如图,点A,B,D分别是△EFC中EF,FC,EC边上的三点,若四边形ABCD是平行四边形,且∠EAD=∠FAB.
(1)请找出图中所有的等腰三角形,并说明理由.
(2)若CF=5,求□ABCD的周长.
分析:要找等腰三角形,只需找图中相等的角,这可结合平行线的性质和已知条件推得;结合题设和等腰三角形的腰长相等便可求得平行四边形的周长.
解:(1)△DAE,△BAF,△CEF都是等腰三角形.
∵四边形ABCD是平行四边形,∴AD∥BC,AB∥CD,
∴∠EAD=∠F,∠FAB=∠E.
∵∠EAD=∠FAB,∴∠EAD=∠F=∠FAB=∠E,
∴△DAE,△BAF,△CEF都是等腰三角形.
(2)∵△DAE,△BAF和△CEF都是等腰三角形,∴AD=DE,AB=BF,CE=CF=5.
∴AB+BC=CD+AD=5,即□ABCD的周长=5+5=10.
同课章节目录
- 第一章 二次根式
- 1.1 二次根式
- 1.2 二次根式的性质
- 1.3 二次根式的运算
- 第二章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程的应用
- 2.4 一元二次方程根与系数的关系(选学)
- 第三章 数据分析初步
- 3.1 平均数
- 3.2 中位数和众数
- 3.3 方差和标准差
- 第四章 平行四边形
- 4.1 多边形
- 4.2 平行四边形
- 4.3 中心对称
- 4.4 平行四边形的判定
- 4.5 三角形的中位线
- 4.6 反证法
- 第五章 特殊平行四边形
- 5.1 矩形
- 5.2 菱形
- 5.3 正方形
- 第六章 反比例函数
- 6.1 反比例函数
- 6.2 反比例函数的图象和性质
- 6.3 反比例函数的应用
