5。4中心对称同步测控及答案

5. 4 中心对称
【要点预习】
1. 中心对称的概念：
如果一个图形绕着一个点旋转180°后，所得到的图形能够和原来的图形互相重合，那么这个图形叫做 ，这个点叫 .
如果一个图形绕着一个已知点旋转180°后，能够和另外一个图形互相重合，那么这两个图形关于该已知点成 .
2. 中心对称的性质：
对称中心平分连结两个 的线段.
【课前热身】
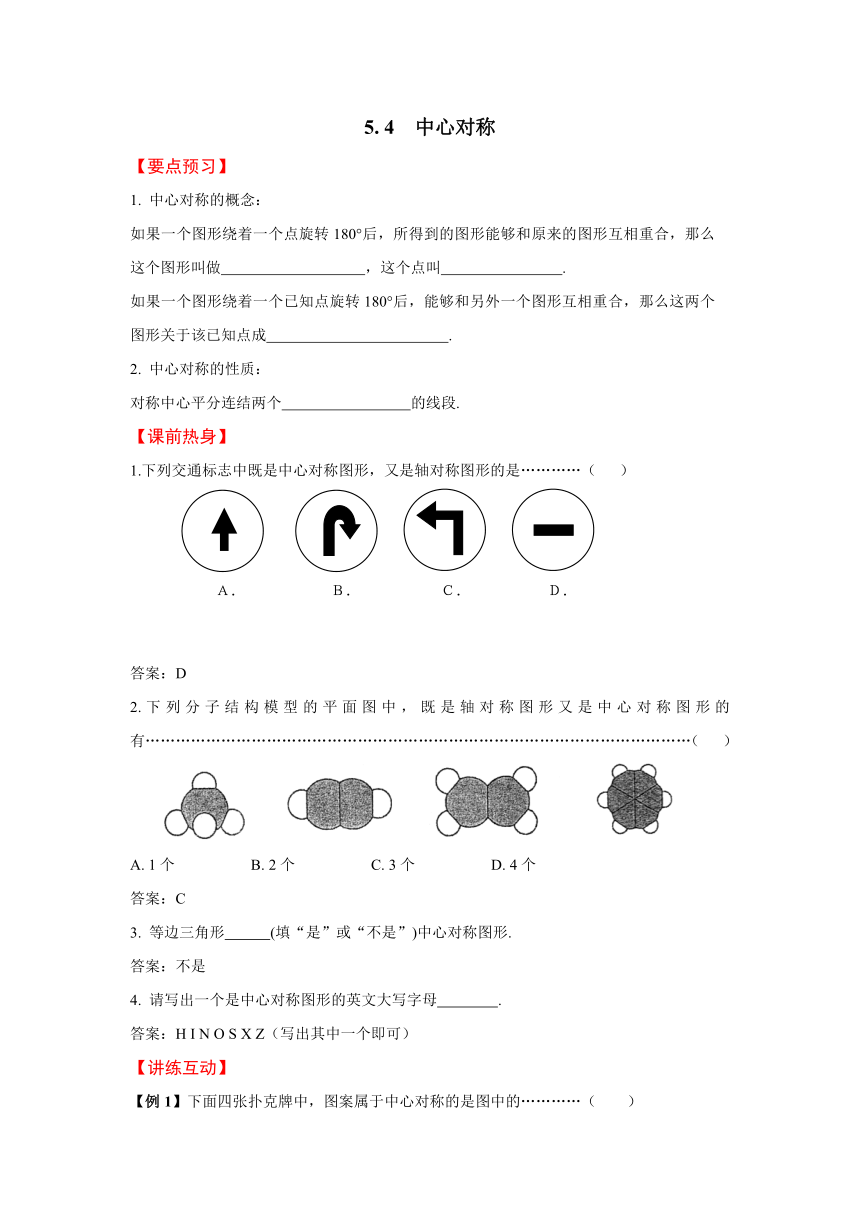
1.下列交通标志中既是中心对称图形，又是轴对称图形的是…………（ 　）
答案：D
2.下列分子结构模型的平面图中，既是轴对称图形又是中心对称图形的有………………………………………………………………………………………………（ ）
A. 1个 B. 2个 C. 3个 D. 4个
答案：C
3. 等边三角形 (填“是”或“不是”)中心对称图形.
答案：不是
4. 请写出一个是中心对称图形的英文大写字母 .
答案：H I N O S X Z（写出其中一个即可）
【讲练互动】
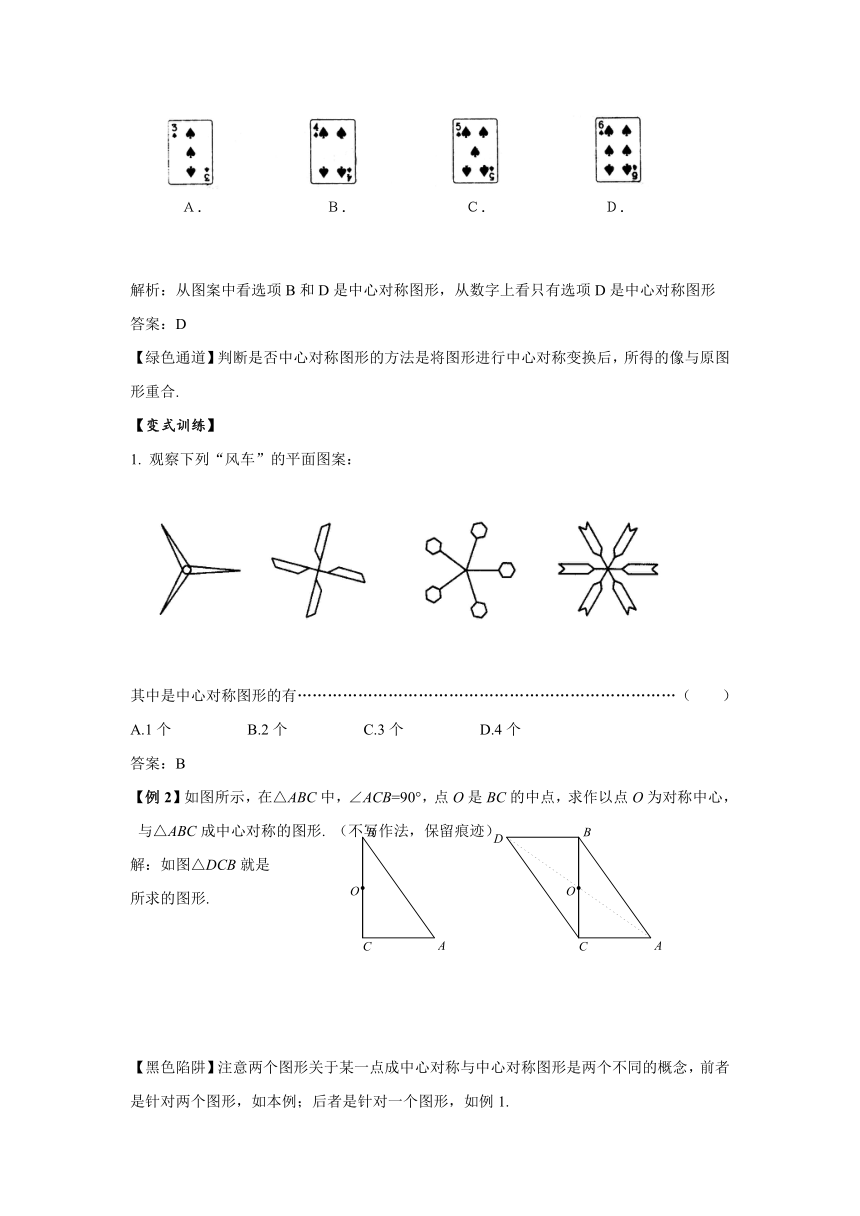
【例1】下面四张扑克牌中，图案属于中心对称的是图中的…………（　　）
解析：从图案中看选项B和D是中心对称图形，从数字上看只有选项D是中心对称图形
答案：D
【绿色通道】判断是否中心对称图形的方法是将图形进行中心对称变换后，所得的像与原图形重合.
【变式训练】
1. 观察下列“风车”的平面图案：

其中是中心对称图形的有…………………………………………………………………（ ）
A.1个 B.2个 C.3个 D.4个
答案：B
【例2】如图所示，在△ABC中，∠ACB=90°，点O是BC的中点，求作以点O为对称中心，与△ABC成中心对称的图形. （不写作法，保留痕迹）
解：如图△DCB就是
所求的图形.
【黑色陷阱】注意两个图形关于某一点成中心对称与中心对称图形是两个不同的概念，前者是针对两个图形，如本例；后者是针对一个图形，如例1.
【变式训练】
2. 某居民小区搞绿化，要在一块矩形空地(如图所示)上建花坛，现征集设计方案，要求设计的方案由圆和正方形组成(个数不限)，并且使整个长方形场地成中心对称图形，请画出你的设计方案.
答案：略
【例3】下三图是由三个相同的小正方形拼成的图形，请你再添加一个同样大小的小正方形，使所得的新图形分别为下列A，B，C题要求的图形，请画出示意图.
（1）是中心对称图形，但不是轴对称图形；
（2）是轴对称图形，但不是中心对称图形；
（3）既是中心对称图形，又是轴对称图形.
解：见下图的阴影部分（取其中一个阴影即可）：
【变式训练】
3.如图，在直角坐标系中，图形①与图形②关于点P成中心对称.
(1)画出对称中心P，并写出点P的坐标；
(2)将图形②向下平移4个单位，画出平移后的图形③，并判断图形③与图形①的位置关系. (直接写出结果)
解：(1)P(1，5)；
(2) 图形③略.
图形③与图形①关于点(1，3)成中心对称.
【同步测控】
基础自测
1. 下列命题中的真命题是…………………………………………………………………（ ）
A. 关于中心对称的两个图形全等 B. 全等的两个图形是中心对称图形
C. 中心对称图形都是轴对称图形 D. 轴对称图形都是中心对称图形
答案：A
2. (2008哈尔滨中考)在下列图形中，既是轴对称图形又是中心对称图形的是…………（ ）
答案：C
3. (2008盐城中考)已知如图1所示的四张牌，若将其中一张牌旋转180°后得到图2，则旋转的牌是…………………………………………………………………………………………（ ）
答案：A
4.下列图形中既是轴对称图形又是中心对称图形的是…………………（ ）
Ａ. 正六边形　　Ｂ. 正五边形　　Ｃ. 平行四边形　　Ｄ. 等腰三角形
答案：A
5.如图是一个中心对称图形，A为对称中心，若∠C=90°，∠B=30°，BC=1，则BB’的长为……………（ ）
A. 4 B. C. D.
答案：D
6. 在英文字母“M”，“N”，“S”，“Z”，“W”中，是中心对称图形的有 个.
答案：3
7.如图，BC为等腰三角形纸片ABC的底边，. 将此三角形纸片沿AD剪开，得到两个三角形，若把这两个三角形拼成一个平面四边形，则能拼出不同的中心对称图形 个.
答案：3
8. 下列图形是不是中心对称图形？若是，请指出对称中心；若不是，请说明理由
(1)线段；(2)等腰三角形；(3)平行四边形；(4)圆.
解：(1)线段是中心对称图形，对称中心中线段的中点；
(2)等腰三角形不是中心对称图形，无论绕哪一点旋转180°后，图形不可能与原图形重合；
(3)平行四边形是中心对称图形，对称中心是对角线的交点；
(4)圆是中心对称图形，对称中心是圆心.
9. 如图，点O在△ABC内. 以O为对称中心，求作与△ABC成中心对称的图形.
解：如图，△DEF就是的图形.
能力提升
10.若一个图形绕着一个定点旋转一个角（）后能够与原来的图形重合，那么这个图形叫做旋转对称图形. 例如：等边三角形绕着它的中心旋转120°（如图），能够与原来的等边三角形重合，因而等边三角形是旋转对称图形. 显然，中心对称图形都是旋转对称图形，但旋转对称图形不一定是中心对称图形. 下面四个图形中，旋转对称图形个数有…………………………………………（ ）

Ａ. 1 Ｂ. 2 Ｃ. 3 Ｄ. 4
解析：第1个图形的旋转角为60°或120°或180°；第2个图形不是中心对称图形，故不是旋转图形；第3个图形的旋转角为120°；第4个图形的旋转角为72°.
答案：C
11. 在平面直角坐标系中，□ABCD的对称中心在原点O，且A（3，2），B（2，-1），请在下面的直角坐标系中画出这个平行四边形，并求点C，D的坐标.
解：如图. C(-3，-2)，D(-2，1).
12.如图（1）所示，是一块边长为2的正方形瓷砖，其中瓷砖的阴影部分是半径为1的扇形. 请你用这种瓷砖拼出两种不同的图案. 使拼成的图案既是轴对称图形又是中心对称图形，并把它们分别画在下面边长为4的正方形（2）（3）中（要求用圆规画图）.
答案：
13. 如图，点O是□ABCD的对称中心，过O任意作直线EF，分别交AD，BC于点E，F，请用平行四边形的中心对称性说明OE=OF.
解：∵点O是□ABCD的对称中心，∴AD 与BC关于O对称.
而过O任意作直线EF，分别交AD，BC于点E，F，∴E，F关于O点对称，
∴OE=OF.
创新应用
14.如图，在4×?3的网格上，由个数相同的白色方块与黑色方块组成一幅图案，请仿照此图案，在下列网格中分别设计出符合要求的图案（注：①不得与原图案相同；②黑、白方块的个数要相同）.
答案：