华师大版数学九年级下册同步课件:26.2.2 第5课时 二次函数最值的应用(共21张PPT)
文档属性
| 名称 | 华师大版数学九年级下册同步课件:26.2.2 第5课时 二次函数最值的应用(共21张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 405.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-27 08:49:07 | ||
图片预览







文档简介
(共21张PPT)
26.2.2 第5课时 二次函数最值的应用
第26章 二次函数
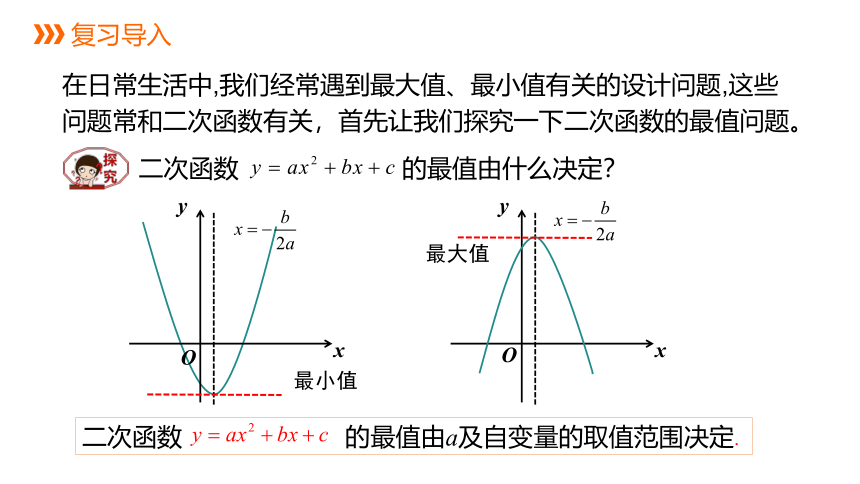
二次函数 的最值由什么决定?
x
y
O
x
y
O
最小值
最大值
二次函数 的最值由a及自变量的取值范围决定.
在日常生活中,我们经常遇到最大值、最小值有关的设计问题,这些问题常和二次函数有关,首先让我们探究一下二次函数的最值问题。
复习导入
问题2 当自变量x为全体实数时,二次函数
的最值是多少?
当a>0时,有 ,此时 .
当a<0时,有 ,此时 .
问题3 当自变量x有限制时,二次函数 的最值如何确定?
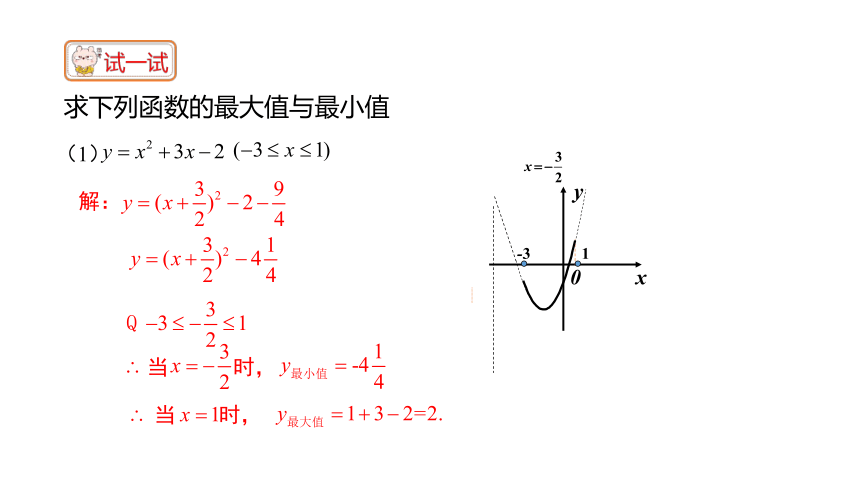
求下列函数的最大值与最小值
x
0
y
解:
-3
1
(1)
当 时,
当 时,
解:
0
x
y
1
-3
(2)
即x在对称轴的右侧.
当 时,
函数的值随着x的增大而减小.
当 时,
问题1 用总长为20m的围栏材料,一面靠墙,围成一个矩形花圃.怎样围才能使花圃的面积最大?
接下来我们看26.1中提出的两个问题.
获取新知
解:这个问题实际上是求出自变量x为何值时,二次函数
y=-2x2+20x (0将这个函数关系式配方,得y=-2(x-5)2+50.
这时,AB=5(m),BC=20-2x=10(m).
因此,当围成的花圃与墙垂直的一边长5m,与墙平行的一边长10m时,花圃的面积最大,最大面积为50m2 .
函数开口向下,顶点坐标时(5,50),
即当x=5时,函数值取得最大值,最大值为y=50
解:这个问题实际上是求出自变量x为何值时,二次函数
取得最大值.
问题2 某商店将每件进价为8元的某种商品按每件10元出售,一天可售出100件.该店想通过降低售价,增加销售量的办法来提高利润.经过市场调查,发现这种商品单价每降低0.1元,其销售量可增加约10件.将这种商品的售价降低多少时,能使销售利润最大
因此,当这种商品的售价降低时,能使销售利润最大,最大利润为225元 .
函数开口向上,顶点坐标是(,225),
∵ 0 ≤ x≤2,
∴x= 时,函数值取得最大值,最大值为y=225.
解:将这个函数关系式配方,得y=-100(x-)2+225.
例1 用长为6米的铝合金材料做一个形状如图所示的矩形窗框.窗框的高于宽各位多少时,它的透光面积最大?最大透光面积是多少?(铝合金型材宽度不计)
x
解:设矩形窗框的宽为x m,则高为 m.这里应有x>0,
故0<x<2.
矩形窗框的透光面积 y与x之间的函数关系式是:
例题讲解
即
配方得
所以,当x=1时,函数取得最大值,最大值y=1.5.
x=1满足0<x<2,这时
因此,所做矩形窗框的宽为1 m、高为1.5 m时,它的透光面积最大,最大面积是1.5 m2.
例2 用总长为60m的篱笆围成矩形场地,矩形面积 S随矩形一边长 l 的变化而变化.当 l 是多少时,场地的面积 S 最大?
分析1 矩形面积公式是什么?
分析2 如何用 l 表示另一边?
分析3 面积 S 的函数关系式是什么?
解:根据题意得
S=l(30-l),
即 S=-l2+30l (0因此,当 时,
S有最大值
也就是说,当l是15m时,场地的面积S最大.
5
10
15
20
25
30
100
200
l
s
O
变式1 如图,用一段长为60m的篱笆围成一个一边靠墙的矩形菜园,墙长32m,这个矩形的长、宽各为多少时,菜园的面积最大,最大面积是多少?
x
x
60-2x
分析2 我们可以设面积为S,如何设自变量?
分析3 面积S的函数关系式是什么?
分析4 如何求解自变量x的取值范围?墙长32m对此题有什么作用?
分析5 如何求最值?
最值在顶点处,即当x=15m时,S=450m2.
分析1 变式1与例1有什么不同?
设垂直于墙的边长为x米,S=x(60-2x)=-2x2+60x.
0<60-2x≤32,即14≤x<30.
变式2 如图,用一段长为60m的篱笆围成一个一边靠墙的矩形菜园,墙长18m,这个矩形的长、宽各为多少时,菜园的面积最大,最大面积是多少?
x
分析1 变式2与变式1有什么异同?
分析2 可否模仿变式1设未知数、列函数关系式?
分析3 可否试设与墙平行的一边为x米?则如何表示另一边?
设矩形面积为Sm2,与墙平行的一边为x米,则
分析4 当x=30时,S取最大值,此结论是否正确?
分析5 如何求自变量的取值范围?
0 < x ≤18.
分析6 如何求最值?
由于30 >18,因此只能利用函数的增减性求其最值.当x=18时,S有最大值是378.
不正确.
实际问题中求解二次函数最值问题,不一定都取图象顶点处,要根据自变量的取值范围.通过变式1与变式2的对比,希望同学们能够理解函数图象的顶点、端点与最值的关系,以及何时取顶点处、何时取端点处才有符合实际的最值.
1.二次函数y=x2-2x+6有最 值(填“大”或“小”),把函数关系式配方得 ,其图象的顶点坐标为 ,故其最值为 .
2.一小球被抛出后,它距离地面的高度h(米)和飞行时间t(秒)满足函数关系式h=-5(t-1)2+6,则小球距离地面的最大高度是( )
A.1米 B.5米 C.6米 D.7米
随堂演练
C
小
y=(x-1)2+5
(1,5)
5
3.手工课上,小明准备做一个形状是菱形的风筝,这个菱形的两条对角线长度之和恰好为60 cm,菱形的面积S(cm2)随其中一条对角线的长x(cm)的变化而变化.
(1)请直接写出S与x之间的函数关系式(不要求写出自变量x的取值范围);
(2)当x的值是多少时,菱形风筝的面积S最大 最大面积是多少
课堂小结
依据常见几何图形的面积公式建立函数关系式
最值有时不在顶点处,则要利用函数的增减性来确定
图形面积的最大值
一个关键
一个注意
26.2.2 第5课时 二次函数最值的应用
第26章 二次函数
二次函数 的最值由什么决定?
x
y
O
x
y
O
最小值
最大值
二次函数 的最值由a及自变量的取值范围决定.
在日常生活中,我们经常遇到最大值、最小值有关的设计问题,这些问题常和二次函数有关,首先让我们探究一下二次函数的最值问题。
复习导入
问题2 当自变量x为全体实数时,二次函数
的最值是多少?
当a>0时,有 ,此时 .
当a<0时,有 ,此时 .
问题3 当自变量x有限制时,二次函数 的最值如何确定?
求下列函数的最大值与最小值
x
0
y
解:
-3
1
(1)
当 时,
当 时,
解:
0
x
y
1
-3
(2)
即x在对称轴的右侧.
当 时,
函数的值随着x的增大而减小.
当 时,
问题1 用总长为20m的围栏材料,一面靠墙,围成一个矩形花圃.怎样围才能使花圃的面积最大?
接下来我们看26.1中提出的两个问题.
获取新知
解:这个问题实际上是求出自变量x为何值时,二次函数
y=-2x2+20x (0
这时,AB=5(m),BC=20-2x=10(m).
因此,当围成的花圃与墙垂直的一边长5m,与墙平行的一边长10m时,花圃的面积最大,最大面积为50m2 .
函数开口向下,顶点坐标时(5,50),
即当x=5时,函数值取得最大值,最大值为y=50
解:这个问题实际上是求出自变量x为何值时,二次函数
取得最大值.
问题2 某商店将每件进价为8元的某种商品按每件10元出售,一天可售出100件.该店想通过降低售价,增加销售量的办法来提高利润.经过市场调查,发现这种商品单价每降低0.1元,其销售量可增加约10件.将这种商品的售价降低多少时,能使销售利润最大
因此,当这种商品的售价降低时,能使销售利润最大,最大利润为225元 .
函数开口向上,顶点坐标是(,225),
∵ 0 ≤ x≤2,
∴x= 时,函数值取得最大值,最大值为y=225.
解:将这个函数关系式配方,得y=-100(x-)2+225.
例1 用长为6米的铝合金材料做一个形状如图所示的矩形窗框.窗框的高于宽各位多少时,它的透光面积最大?最大透光面积是多少?(铝合金型材宽度不计)
x
解:设矩形窗框的宽为x m,则高为 m.这里应有x>0,
故0<x<2.
矩形窗框的透光面积 y与x之间的函数关系式是:
例题讲解
即
配方得
所以,当x=1时,函数取得最大值,最大值y=1.5.
x=1满足0<x<2,这时
因此,所做矩形窗框的宽为1 m、高为1.5 m时,它的透光面积最大,最大面积是1.5 m2.
例2 用总长为60m的篱笆围成矩形场地,矩形面积 S随矩形一边长 l 的变化而变化.当 l 是多少时,场地的面积 S 最大?
分析1 矩形面积公式是什么?
分析2 如何用 l 表示另一边?
分析3 面积 S 的函数关系式是什么?
解:根据题意得
S=l(30-l),
即 S=-l2+30l (0
S有最大值
也就是说,当l是15m时,场地的面积S最大.
5
10
15
20
25
30
100
200
l
s
O
变式1 如图,用一段长为60m的篱笆围成一个一边靠墙的矩形菜园,墙长32m,这个矩形的长、宽各为多少时,菜园的面积最大,最大面积是多少?
x
x
60-2x
分析2 我们可以设面积为S,如何设自变量?
分析3 面积S的函数关系式是什么?
分析4 如何求解自变量x的取值范围?墙长32m对此题有什么作用?
分析5 如何求最值?
最值在顶点处,即当x=15m时,S=450m2.
分析1 变式1与例1有什么不同?
设垂直于墙的边长为x米,S=x(60-2x)=-2x2+60x.
0<60-2x≤32,即14≤x<30.
变式2 如图,用一段长为60m的篱笆围成一个一边靠墙的矩形菜园,墙长18m,这个矩形的长、宽各为多少时,菜园的面积最大,最大面积是多少?
x
分析1 变式2与变式1有什么异同?
分析2 可否模仿变式1设未知数、列函数关系式?
分析3 可否试设与墙平行的一边为x米?则如何表示另一边?
设矩形面积为Sm2,与墙平行的一边为x米,则
分析4 当x=30时,S取最大值,此结论是否正确?
分析5 如何求自变量的取值范围?
0 < x ≤18.
分析6 如何求最值?
由于30 >18,因此只能利用函数的增减性求其最值.当x=18时,S有最大值是378.
不正确.
实际问题中求解二次函数最值问题,不一定都取图象顶点处,要根据自变量的取值范围.通过变式1与变式2的对比,希望同学们能够理解函数图象的顶点、端点与最值的关系,以及何时取顶点处、何时取端点处才有符合实际的最值.
1.二次函数y=x2-2x+6有最 值(填“大”或“小”),把函数关系式配方得 ,其图象的顶点坐标为 ,故其最值为 .
2.一小球被抛出后,它距离地面的高度h(米)和飞行时间t(秒)满足函数关系式h=-5(t-1)2+6,则小球距离地面的最大高度是( )
A.1米 B.5米 C.6米 D.7米
随堂演练
C
小
y=(x-1)2+5
(1,5)
5
3.手工课上,小明准备做一个形状是菱形的风筝,这个菱形的两条对角线长度之和恰好为60 cm,菱形的面积S(cm2)随其中一条对角线的长x(cm)的变化而变化.
(1)请直接写出S与x之间的函数关系式(不要求写出自变量x的取值范围);
(2)当x的值是多少时,菱形风筝的面积S最大 最大面积是多少
课堂小结
依据常见几何图形的面积公式建立函数关系式
最值有时不在顶点处,则要利用函数的增减性来确定
图形面积的最大值
一个关键
一个注意
