第六章特殊平行四边形和梯形单元同步测控及答案
文档属性
| 名称 | 第六章特殊平行四边形和梯形单元同步测控及答案 | 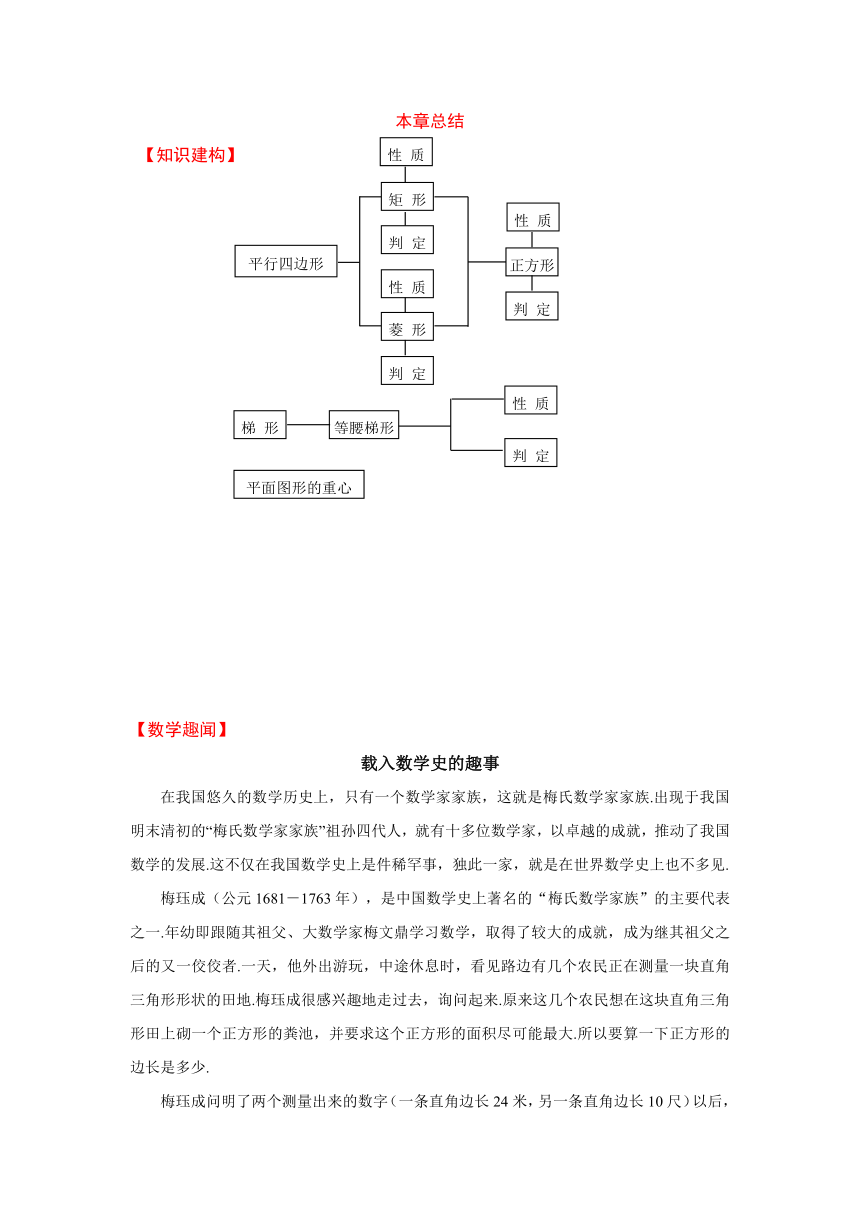 | |
| 格式 | zip | ||
| 文件大小 | 119.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-04-26 09:08:41 | ||
图片预览




文档简介
本章总结
【知识建构】
【数学趣闻】
载入数学史的趣事
在我国悠久的数学历史上,只有一个数学家家族,这就是梅氏数学家家族.出现于我国明末清初的“梅氏数学家家族”祖孙四代人,就有十多位数学家,以卓越的成就,推动了我国数学的发展.这不仅在我国数学史上是件稀罕事,独此一家,就是在世界数学史上也不多见.
梅珏成(公元1681-1763年),是中国数学史上著名的“梅氏数学家族”的主要代表之一.年幼即跟随其祖父、大数学家梅文鼎学习数学,取得了较大的成就,成为继其祖父之后的又一佼佼者.一天,他外出游玩,中途休息时,看见路边有几个农民正在测量一块直角三角形形状的田地.梅珏成很感兴趣地走过去,询问起来.原来这几个农民想在这块直角三角形田上砌一个正方形的粪池,并要求这个正方形的面积尽可能最大.所以要算一下正方形的边长是多少. 梅珏成问明了两个测量出来的数字(一条直角边长24米,另一条直角边长10尺)以后,说:“这很简单,只要设所求的正方形边长为x,利用两个相似三角形的对应边成比例关系,立即可得:24:x=10:(10-x),x=10×24/10+24=120/17(尺),即为所求.”
几个农民听完后,连声称赞道:“先生真了不起!我们对算术可是一窍不通,平时全靠这孩子帮忙,他可没您算得快.”
梅珏成这才注意到旁边的那个男孩子,于是笑了笑说:“小先生,你算出来的,是不是也一样呀?”小男孩子点点头,说:“是一样.但我不懂什么相似三角形.我是这样算的.”小男孩子一边说,一边用树枝在地上画起来:把三角形分成三块,每块两个,拼成一个大正方形.这样一下子就可以看出,大长方形面积是原三角形的两倍,要求的边长(也就是大长方形的宽)则等于大长方形的面积除以它的底长,即?=10×24/10+24=120/17(尺)
梅珏成看完后非常惊讶:真是直观和巧妙极了,而且简单易懂!当他得知,早在一千多年以前的三国时期,大数学家刘徽就已运用了这种“面积割补法”时,兴奋极了.回宫后,也立即将这个问题及解法写进正在编写的书中.祖孙四代的梅氏数学家家族,是我们中华民族的骄傲,它为祖国文化所做出的巨大贡献,值得我们赞扬!而小男孩巧解题一事也因巧遇梅珏成而载入我国数学史册,成为美谈.
【本章测评】(单元活页卷)
一、选择题(每题3分,共30分)
1. 矩形具有一般平行四边形不具有的性质是……………………………………………( )
A. 对边相互平行 B. 对角线相等 C. 对角线相互平分 D. 对角相等
答案:B
2.顺次连接对角线互相垂直的四边形各边中点,所得到的四边形一定是( )
A. 梯形 B. 菱形 C. 矩形 D. 正方形
答案:C
3.菱形两条对角线的长分别为6和8,则这个菱形的周长为……………( )
A.18 B.20 C.22 D.24
答案:B
4.如图,已知四边形ABCD是平行四边形,下列结论中不正确的是………………………………………( )
A.当AB=BC时,它是菱形 B.当AC⊥BD时,它是菱形
C.当∠ABC=90°时,它是矩形 D.当AC=BD时,它是正方形
答案:D
5.在平面直角坐标系中,已知点A(0,2),B(,0),C(0,),D(,0),则以这四个点为顶点的四边形是……………………………………( )
A.矩形 B.菱形 C.正方形 D.梯形
答案:B
6.如果等腰梯形两底差的一半等于它的高,那么这个梯形的一个底角等于……………( )
A.75° B.60° C.45° D.30°
解析:如图,作DE∥AB,DF⊥BC于F.则可得四边形ABED是平行四边形,得BE=AD,DE=AB=CD,于是BF=FC,根据题意得DF=FC,可求得∠C=45°.
答案:C
7.下列命题正确的是………………………………………………………( )
A.对角线相等且互相平分的四边形是菱形 B.对角线相等且互相垂直的四边形是菱形
C.对角线相等且互相平分的四边形是矩形 D.对角线相等的四边形是等腰梯形
答案:C
8.如图,在等腰梯形ABCD中,AD∥BC,AD=3,BC=5,AC,BD 相交于O点,且∠BOC=60°,顺次连结等腰梯形各边中点所得四边形的周长是………………………………………( )
A.24 B.20 C.16 D.12
解析:如图,作DE∥AC交BC延长线于E,则四边形ACED是平行四边形,得DE=BD=AC,CE=AD=3,于是BE=8,而∠BDE=∠BOC= 60°,故△BDE是正三角形,得AC=BD=BE=8,于是根据三角形的中位线定理可求得连结等腰梯形各边中点所得四边形的周长.
答案:C
9.当身边没有量角器时,怎样得到一些特定度数的角呢?动手操作有时可以解“燃眉之急”.如图,已知矩形ABCD,我们按如下步骤操作可以得到一个特定的角:(1)以点A所在直线为折痕,折叠纸片,使点B落在AD上,折痕与BC交于E;(2)将纸片展平后,再一次折叠纸片,以E所在直线为折痕,使点A落在BC上,折痕EF交AD于F.则∠AFE =…………………………………………………………( )
A.60( B.67.5( C.72( D.75(
解析:根据步骤作出图形,由题意可知AE,EF分别是∠BAD和∠AEC的角平分线,于是∠AFE=∠FEC= ∠AEC=67.5(.
答案:B
10.如图,在直角梯形ABCD中AD∥BC,点E是边CD 的中点,若AB=AD+BC,BE=,则梯形ABCD的面积为………………( )
A. B. C. D.25
解析:如图,连结并延长AE交BC延长线于F,则可证△ADE≌△FCE,得AD=FC,AE=EF,于是AB=BF,而∠ABC=90(,BE=,故AF=5,AB==BF,于是可求得梯形ABCD的面积.
答案:A
二、填空题(每题3分,共30分)
11. 矩形的两邻边分别为8㎝和6㎝,则其对角线为 ㎝,矩形面积为 cm2.
答案:10 48
12.Rt△ABC中,两条直角边AC,BC的长分别为cm与2cm,点D是斜边AB上的中点,则CD= cm.
答案:
13.已知菱形ABCD的面积是12cm2,对角线AC=4cm,则菱形的边长是 cm.
答案:
14.如图,矩形纸片ABCD中,AD=9,AB=3,将其折叠,使点D与点B重合,折痕为EF,那么折痕EF的长为________.
答案:
15. 如图,菱形花坛ABCD的边长为6m,∠B=60°,其中由两个正六边形组成的图形部分种花,则种花部分的图形的周长为_______.
答案:20m
16.如图,正方形的边长为3cm,,且,则= cm.
答案:3
17. 如图,P是正方形ABCD内一点,将△ABP绕点B顺时针方向旋转能与△CBP′重合,若PB=3,则PP/= .
解析:由题意可得PB=P/B=3,∠PBP/=90°,由勾股定理求得PP/=3.
答案:3
18.若等腰梯形ABCD的上、下底之和为4,并且两条对角线所夹锐角为60°,则该等腰梯形的面积为 .
解析:如图,作DE∥AC交BC延长线于E,则四边形ACED是平行四边形,得DE=BD=AC,CE=AD,于是BE=4,而∠BDE=∠BOC= 60°,故△BDE是正三角形,故梯形的面积即为正△BDE的面积.
答案:
19.如图,梯形ABCD中,AB∥DC,∠ADC+∠BCD=90°,且DC=2AB,分别以DA、AB、BC为边向梯形外作正方形,其面积分别为、、,则、、之间的关系是 .
解析:过A作AE∥BC,易证得DE=CE=AB,∠DAE=90°,于是可得AD2+AE2=DE2,即AD2+BC2 =AB2,亦即S1+S3=S2.
答案:S1+S3=S2
20.如图,菱形ABCD中,∠BAD=60o,M是AB的中点,P是对角线AC上的一个动点,若PM+PB的最小值是3,则AB长为 .
解析:连结PD,则易证△CPB≌△CPD,得PB=PD,故PM+PD的最小值即DM为3,易得△DAM是30 o的直角三角形,故AB=AD=.
答案:
三、解答题(共40分)
21. 如图,四边形ABCD为矩形,∠ABD=60°,BD=10.
求AB、AD和面积.
解:∵四边形ABCD为矩形,
∴∠BAC=90°,BO=OD=OA=OC=5.
∵∠ABD=60°,∴△AOB是正三角形,∴AB=AO=5.
∴AD=.
22.如图,把一张矩形的纸ABCD沿对角线BD折叠,使点C落在点E处,BE与AD交于点F.
⑴求证:ΔABF≌ΔEDF;
⑵若将折叠的图形恢复原状,点F与BC边上的点M正好重合,连接DM,试判断四边形BMDF的形状,并说明理由.
(1)证明:由题意得DE=DC=AB,∠A=∠E=90°,
又∵∠AFB=∠EFD,∴△ABF≌△EDF.
(2)菱形.
证明:∵BE∥DM,AD∥BC,∴四边形BMDF是平行四边形.
∵△ABF≌△EDF,∴BF=DF.
∴四边形BMDF是菱形.
23.如图所示,在△ABC中,分别以AB、AC、BC为边在BC的同侧作等边△ABD,等边△ACE、等边△BCF.
(1)求证:四边形DAEF是平行四边形;
(2)探究下列问题:(只填满足的条件,不需证明)
①当△ABC满足_______________________条件时,四边形DAEF是矩形;
②当△ABC满足_______________________条件时,四边形DAEF是菱形;
③当△ABC满足________________________条件时,四边形DAEF是正方形;
④当△ABC满足_______________________条件时,以D、A、E、F为顶点的四边形不存在.
(1)证明:∵△ABD和△FBC都是等边三角形,
∴∠DBF+∠FBA=∠ABC+∠FBA=60°,∴∠DBF=∠ABC.
又∵BD=BA,BF=BC,∴△ABC≌△DBF,∴AC=DF=AE.
同理△ABC≌△EFC,∴AB=EF=AD.
∴四边形ADFE是平行四边形.
(2)①∠BAC=150° ②AB=AC≠BC ③∠BAC=60°
24. 如图甲,四边形ABCD是等腰梯形,AB∥DC. 由4个这样的等腰梯形可以拼出图乙所示的平行四边形.
(1)求四边形ABCD四个内角的度数;
(2)试探究四边形ABCD四条边之间存在的等量关系,并说明理由;
(3)现有图甲中的等腰梯形若干个,利用它们你能拼出一个菱形吗?若能,请你画出大致的示意图.
解:(1)由图乙知3∠C=360°,得∠C=120°=∠D.
∵AB∥DC,∴∠A+∠D=180°,∴∠A=60°=∠B.
(2)由图乙知AD=DC=CB.
过C作CE∥AD,则四边形ADCE是平行四边形.
∴AE=DC=AD=CE=CB,故AB=2AD=2DC=2CB.
(3)由于图乙的边长之比为2:3,如图.
25. (1)如图1,图2,图3,在中,分别以为边,向外作正三角形,正四边形,正五边形,相交于点.
①如图1,求证:;
②探究:如图1, ;
如图2, ;
如图3, .
(2)如图4,已知:是以为边向外所作正边形的一组邻边;是以为边向外所作正边形的一组邻边.的延长相交于点.
①猜想:如图4, (用含的式子表示);
②根据图4证明你的猜想.
(1)①证明:与均为等边三角形,
∴AD=AB,AC=AE且
,
即,.
②,,.
(2)①
②证明:依题意,知和都是正边形的内角,,,
,即. .
,,
,
【知识建构】
【数学趣闻】
载入数学史的趣事
在我国悠久的数学历史上,只有一个数学家家族,这就是梅氏数学家家族.出现于我国明末清初的“梅氏数学家家族”祖孙四代人,就有十多位数学家,以卓越的成就,推动了我国数学的发展.这不仅在我国数学史上是件稀罕事,独此一家,就是在世界数学史上也不多见.
梅珏成(公元1681-1763年),是中国数学史上著名的“梅氏数学家族”的主要代表之一.年幼即跟随其祖父、大数学家梅文鼎学习数学,取得了较大的成就,成为继其祖父之后的又一佼佼者.一天,他外出游玩,中途休息时,看见路边有几个农民正在测量一块直角三角形形状的田地.梅珏成很感兴趣地走过去,询问起来.原来这几个农民想在这块直角三角形田上砌一个正方形的粪池,并要求这个正方形的面积尽可能最大.所以要算一下正方形的边长是多少. 梅珏成问明了两个测量出来的数字(一条直角边长24米,另一条直角边长10尺)以后,说:“这很简单,只要设所求的正方形边长为x,利用两个相似三角形的对应边成比例关系,立即可得:24:x=10:(10-x),x=10×24/10+24=120/17(尺),即为所求.”
几个农民听完后,连声称赞道:“先生真了不起!我们对算术可是一窍不通,平时全靠这孩子帮忙,他可没您算得快.”
梅珏成这才注意到旁边的那个男孩子,于是笑了笑说:“小先生,你算出来的,是不是也一样呀?”小男孩子点点头,说:“是一样.但我不懂什么相似三角形.我是这样算的.”小男孩子一边说,一边用树枝在地上画起来:把三角形分成三块,每块两个,拼成一个大正方形.这样一下子就可以看出,大长方形面积是原三角形的两倍,要求的边长(也就是大长方形的宽)则等于大长方形的面积除以它的底长,即?=10×24/10+24=120/17(尺)
梅珏成看完后非常惊讶:真是直观和巧妙极了,而且简单易懂!当他得知,早在一千多年以前的三国时期,大数学家刘徽就已运用了这种“面积割补法”时,兴奋极了.回宫后,也立即将这个问题及解法写进正在编写的书中.祖孙四代的梅氏数学家家族,是我们中华民族的骄傲,它为祖国文化所做出的巨大贡献,值得我们赞扬!而小男孩巧解题一事也因巧遇梅珏成而载入我国数学史册,成为美谈.
【本章测评】(单元活页卷)
一、选择题(每题3分,共30分)
1. 矩形具有一般平行四边形不具有的性质是……………………………………………( )
A. 对边相互平行 B. 对角线相等 C. 对角线相互平分 D. 对角相等
答案:B
2.顺次连接对角线互相垂直的四边形各边中点,所得到的四边形一定是( )
A. 梯形 B. 菱形 C. 矩形 D. 正方形
答案:C
3.菱形两条对角线的长分别为6和8,则这个菱形的周长为……………( )
A.18 B.20 C.22 D.24
答案:B
4.如图,已知四边形ABCD是平行四边形,下列结论中不正确的是………………………………………( )
A.当AB=BC时,它是菱形 B.当AC⊥BD时,它是菱形
C.当∠ABC=90°时,它是矩形 D.当AC=BD时,它是正方形
答案:D
5.在平面直角坐标系中,已知点A(0,2),B(,0),C(0,),D(,0),则以这四个点为顶点的四边形是……………………………………( )
A.矩形 B.菱形 C.正方形 D.梯形
答案:B
6.如果等腰梯形两底差的一半等于它的高,那么这个梯形的一个底角等于……………( )
A.75° B.60° C.45° D.30°
解析:如图,作DE∥AB,DF⊥BC于F.则可得四边形ABED是平行四边形,得BE=AD,DE=AB=CD,于是BF=FC,根据题意得DF=FC,可求得∠C=45°.
答案:C
7.下列命题正确的是………………………………………………………( )
A.对角线相等且互相平分的四边形是菱形 B.对角线相等且互相垂直的四边形是菱形
C.对角线相等且互相平分的四边形是矩形 D.对角线相等的四边形是等腰梯形
答案:C
8.如图,在等腰梯形ABCD中,AD∥BC,AD=3,BC=5,AC,BD 相交于O点,且∠BOC=60°,顺次连结等腰梯形各边中点所得四边形的周长是………………………………………( )
A.24 B.20 C.16 D.12
解析:如图,作DE∥AC交BC延长线于E,则四边形ACED是平行四边形,得DE=BD=AC,CE=AD=3,于是BE=8,而∠BDE=∠BOC= 60°,故△BDE是正三角形,得AC=BD=BE=8,于是根据三角形的中位线定理可求得连结等腰梯形各边中点所得四边形的周长.
答案:C
9.当身边没有量角器时,怎样得到一些特定度数的角呢?动手操作有时可以解“燃眉之急”.如图,已知矩形ABCD,我们按如下步骤操作可以得到一个特定的角:(1)以点A所在直线为折痕,折叠纸片,使点B落在AD上,折痕与BC交于E;(2)将纸片展平后,再一次折叠纸片,以E所在直线为折痕,使点A落在BC上,折痕EF交AD于F.则∠AFE =…………………………………………………………( )
A.60( B.67.5( C.72( D.75(
解析:根据步骤作出图形,由题意可知AE,EF分别是∠BAD和∠AEC的角平分线,于是∠AFE=∠FEC= ∠AEC=67.5(.
答案:B
10.如图,在直角梯形ABCD中AD∥BC,点E是边CD 的中点,若AB=AD+BC,BE=,则梯形ABCD的面积为………………( )
A. B. C. D.25
解析:如图,连结并延长AE交BC延长线于F,则可证△ADE≌△FCE,得AD=FC,AE=EF,于是AB=BF,而∠ABC=90(,BE=,故AF=5,AB==BF,于是可求得梯形ABCD的面积.
答案:A
二、填空题(每题3分,共30分)
11. 矩形的两邻边分别为8㎝和6㎝,则其对角线为 ㎝,矩形面积为 cm2.
答案:10 48
12.Rt△ABC中,两条直角边AC,BC的长分别为cm与2cm,点D是斜边AB上的中点,则CD= cm.
答案:
13.已知菱形ABCD的面积是12cm2,对角线AC=4cm,则菱形的边长是 cm.
答案:
14.如图,矩形纸片ABCD中,AD=9,AB=3,将其折叠,使点D与点B重合,折痕为EF,那么折痕EF的长为________.
答案:
15. 如图,菱形花坛ABCD的边长为6m,∠B=60°,其中由两个正六边形组成的图形部分种花,则种花部分的图形的周长为_______.
答案:20m
16.如图,正方形的边长为3cm,,且,则= cm.
答案:3
17. 如图,P是正方形ABCD内一点,将△ABP绕点B顺时针方向旋转能与△CBP′重合,若PB=3,则PP/= .
解析:由题意可得PB=P/B=3,∠PBP/=90°,由勾股定理求得PP/=3.
答案:3
18.若等腰梯形ABCD的上、下底之和为4,并且两条对角线所夹锐角为60°,则该等腰梯形的面积为 .
解析:如图,作DE∥AC交BC延长线于E,则四边形ACED是平行四边形,得DE=BD=AC,CE=AD,于是BE=4,而∠BDE=∠BOC= 60°,故△BDE是正三角形,故梯形的面积即为正△BDE的面积.
答案:
19.如图,梯形ABCD中,AB∥DC,∠ADC+∠BCD=90°,且DC=2AB,分别以DA、AB、BC为边向梯形外作正方形,其面积分别为、、,则、、之间的关系是 .
解析:过A作AE∥BC,易证得DE=CE=AB,∠DAE=90°,于是可得AD2+AE2=DE2,即AD2+BC2 =AB2,亦即S1+S3=S2.
答案:S1+S3=S2
20.如图,菱形ABCD中,∠BAD=60o,M是AB的中点,P是对角线AC上的一个动点,若PM+PB的最小值是3,则AB长为 .
解析:连结PD,则易证△CPB≌△CPD,得PB=PD,故PM+PD的最小值即DM为3,易得△DAM是30 o的直角三角形,故AB=AD=.
答案:
三、解答题(共40分)
21. 如图,四边形ABCD为矩形,∠ABD=60°,BD=10.
求AB、AD和面积.
解:∵四边形ABCD为矩形,
∴∠BAC=90°,BO=OD=OA=OC=5.
∵∠ABD=60°,∴△AOB是正三角形,∴AB=AO=5.
∴AD=.
22.如图,把一张矩形的纸ABCD沿对角线BD折叠,使点C落在点E处,BE与AD交于点F.
⑴求证:ΔABF≌ΔEDF;
⑵若将折叠的图形恢复原状,点F与BC边上的点M正好重合,连接DM,试判断四边形BMDF的形状,并说明理由.
(1)证明:由题意得DE=DC=AB,∠A=∠E=90°,
又∵∠AFB=∠EFD,∴△ABF≌△EDF.
(2)菱形.
证明:∵BE∥DM,AD∥BC,∴四边形BMDF是平行四边形.
∵△ABF≌△EDF,∴BF=DF.
∴四边形BMDF是菱形.
23.如图所示,在△ABC中,分别以AB、AC、BC为边在BC的同侧作等边△ABD,等边△ACE、等边△BCF.
(1)求证:四边形DAEF是平行四边形;
(2)探究下列问题:(只填满足的条件,不需证明)
①当△ABC满足_______________________条件时,四边形DAEF是矩形;
②当△ABC满足_______________________条件时,四边形DAEF是菱形;
③当△ABC满足________________________条件时,四边形DAEF是正方形;
④当△ABC满足_______________________条件时,以D、A、E、F为顶点的四边形不存在.
(1)证明:∵△ABD和△FBC都是等边三角形,
∴∠DBF+∠FBA=∠ABC+∠FBA=60°,∴∠DBF=∠ABC.
又∵BD=BA,BF=BC,∴△ABC≌△DBF,∴AC=DF=AE.
同理△ABC≌△EFC,∴AB=EF=AD.
∴四边形ADFE是平行四边形.
(2)①∠BAC=150° ②AB=AC≠BC ③∠BAC=60°
24. 如图甲,四边形ABCD是等腰梯形,AB∥DC. 由4个这样的等腰梯形可以拼出图乙所示的平行四边形.
(1)求四边形ABCD四个内角的度数;
(2)试探究四边形ABCD四条边之间存在的等量关系,并说明理由;
(3)现有图甲中的等腰梯形若干个,利用它们你能拼出一个菱形吗?若能,请你画出大致的示意图.
解:(1)由图乙知3∠C=360°,得∠C=120°=∠D.
∵AB∥DC,∴∠A+∠D=180°,∴∠A=60°=∠B.
(2)由图乙知AD=DC=CB.
过C作CE∥AD,则四边形ADCE是平行四边形.
∴AE=DC=AD=CE=CB,故AB=2AD=2DC=2CB.
(3)由于图乙的边长之比为2:3,如图.
25. (1)如图1,图2,图3,在中,分别以为边,向外作正三角形,正四边形,正五边形,相交于点.
①如图1,求证:;
②探究:如图1, ;
如图2, ;
如图3, .
(2)如图4,已知:是以为边向外所作正边形的一组邻边;是以为边向外所作正边形的一组邻边.的延长相交于点.
①猜想:如图4, (用含的式子表示);
②根据图4证明你的猜想.
(1)①证明:与均为等边三角形,
∴AD=AB,AC=AE且
,
即,.
②,,.
(2)①
②证明:依题意,知和都是正边形的内角,,,
,即. .
,,
,
同课章节目录
- 第一章 二次根式
- 1.1 二次根式
- 1.2 二次根式的性质
- 1.3 二次根式的运算
- 第二章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程的应用
- 2.4 一元二次方程根与系数的关系(选学)
- 第三章 数据分析初步
- 3.1 平均数
- 3.2 中位数和众数
- 3.3 方差和标准差
- 第四章 平行四边形
- 4.1 多边形
- 4.2 平行四边形
- 4.3 中心对称
- 4.4 平行四边形的判定
- 4.5 三角形的中位线
- 4.6 反证法
- 第五章 特殊平行四边形
- 5.1 矩形
- 5.2 菱形
- 5.3 正方形
- 第六章 反比例函数
- 6.1 反比例函数
- 6.2 反比例函数的图象和性质
- 6.3 反比例函数的应用
