第一章 二次根式 章末复习课件(共34张PPT)
文档属性
| 名称 | 第一章 二次根式 章末复习课件(共34张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-05-24 11:23:55 | ||
图片预览











文档简介
(共34张PPT)
第一章 二次根式
章末复习课件
浙教版 八年级下册
知识梳理
知识梳理
Part 1
知识梳理
知识点1 二次根式的定义
一般地,我们把形如 的式子叫做二次根式.
“ ”称为二次根号.
(a≥0)
1.两个必备特征
①外貌特征:含有“ ”
②内在特征:被开方数a ≥0
知识梳理
≥0
≥0
算术平方根
3.判断一个式子是否为二次根式,应该从两个方面进行考虑:
2.(a≥0)既是一个二次根式,又表示非负数a的_____________,所以具有“双重非负性”,即:a_____, _____.
①是否带有“ ”;
②被开方数是否为非负数.
对点训练
1.下列式子:
,其中是二次根式的有( )
A.1个 B.3个 C.4个 D.5个
B
2.要使式子 有意义,则x应该满足____________.
x≥2且 x ≠3
知识梳理
知识点2 二次根式的性质
一般地, =a (a ≥0).
即一个非负数的算术平方根的平方等于它本身.
注意:不要忽略a≥0这一限制条件.这是使二次根式
有意义的前提条件.
知识梳理
a (a≥0)
-a (a<0)
即任意一个数的平方的算术平方根等于它本身的绝对值.
知识梳理
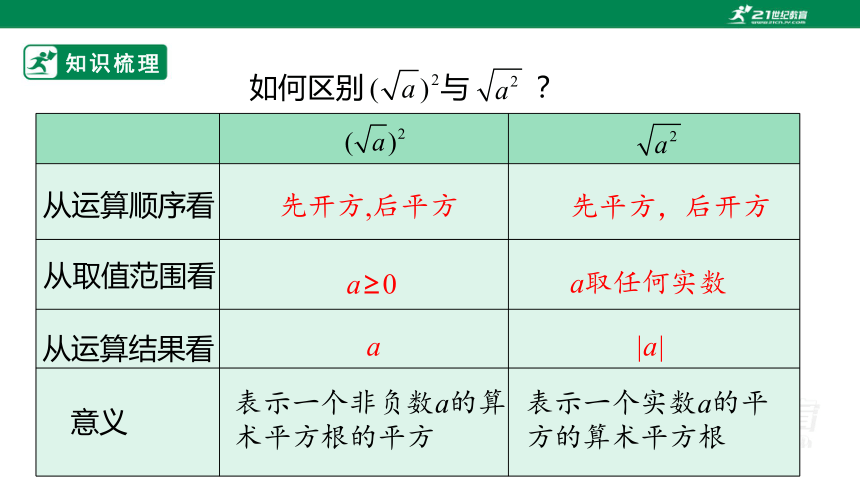
如何区别 与 ?
从运算顺序看
从取值范围看
从运算结果看
先开方,后平方
先平方,后开方
a≥0
a取任何实数
a
|a|
意义
表示一个非负数a的算术平方根的平方
表示一个实数a的平方的算术平方根
知识梳理
积的算术平方根的性质:
商的算术平方根的性质:
即:
最简二次根式:
在根号内不含分母,不含开得尽方的因数或因式,这样的二次根式我们就说它是最简二次根式.
二次根式化简的结果应为最简二次根式。
对点训练
C
C
对点训练
D
B
知识梳理
知识点3 二次根式的运算
语言表述:算术平方根的积等于各个被开方数积的算术平方根.
二次根式的乘法法则:
二次根式相乘,__________不变,____________相乘.
根指数
被开方数
注意:a,b都必须是非负数.
反过来:
(a≥0,b≥0)
语言表述:积的算术平方根,等于积中各因式的算术平方根的积.
知识梳理
二次根式的乘法法则的推广:
①多个二次根式相乘时此法则也适用,即
②当二次根号外有因数(式)时,可以类比单项式乘单项式的法则计算,即根号外的因数(式)的积作为根号外的因数(式),被开方数的积作为被开方数,即
知识梳理
二次根式的除法法则:
算术平方根的商等于被开方数商的算术平方根.
当二次根式根号外的因数(式)不为1时,可类比单项式除以单项式法则,易得
知识梳理
商的算术平方根,等于积中各因式的算术平方根的商.
反过来,就得到
二次根式的商的算术平方根的性质:
知识梳理
二次根式的加减法法则:
一般地,二次根式加减时,可以先将二次根式化成最简二次根式,再将被开方数相同的二次根式进行合并.
(1)化——将非最简二次根式的二次根式化简;
加减法的运算步骤:
(2)找——找出被开方数相同的二次根式;
(3)并——把被开方数相同的二次根式合并.
一化简
二判断
三合并
依据:二次根式的性质、分配律和整式加减法则.
知识梳理
(1)二次根式混合运算的运算次序是:先乘除,后加减;
(2)整式运算的运算法则和运算律对二次根式同样适用。
(3)二次根式的运算结果能化简的必须化简。
二次根式的混合运算:
知识梳理
常见的乘法公式或法则:
(1)m(a+b+c)=_____________________;
(2)(x+a)(x+b)=_______________________;
(3)(a+b)(a-b)=_______________;
(4)(a±b)2=_______________________.
ma+mb+mc
x2+(a+b)x+ab
a2-b2
a2±2ab+b2
对点训练
B
6
D
对点训练
9
A
对点训练
6.计算:
知识梳理
知识点4 二次根式的应用
运用二次根式解决简单的实际问题时应注意的问题
1.读懂题意
2.分析解题思路
3.写出解题过程
对点训练
B
对点训练
提升训练
提升训练
Part 2
提升训练
C
A
提升训练
A
±1
提升训练
提升训练
C
提升训练
提升训练
提升训练
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
第一章 二次根式
章末复习课件
浙教版 八年级下册
知识梳理
知识梳理
Part 1
知识梳理
知识点1 二次根式的定义
一般地,我们把形如 的式子叫做二次根式.
“ ”称为二次根号.
(a≥0)
1.两个必备特征
①外貌特征:含有“ ”
②内在特征:被开方数a ≥0
知识梳理
≥0
≥0
算术平方根
3.判断一个式子是否为二次根式,应该从两个方面进行考虑:
2.(a≥0)既是一个二次根式,又表示非负数a的_____________,所以具有“双重非负性”,即:a_____, _____.
①是否带有“ ”;
②被开方数是否为非负数.
对点训练
1.下列式子:
,其中是二次根式的有( )
A.1个 B.3个 C.4个 D.5个
B
2.要使式子 有意义,则x应该满足____________.
x≥2且 x ≠3
知识梳理
知识点2 二次根式的性质
一般地, =a (a ≥0).
即一个非负数的算术平方根的平方等于它本身.
注意:不要忽略a≥0这一限制条件.这是使二次根式
有意义的前提条件.
知识梳理
a (a≥0)
-a (a<0)
即任意一个数的平方的算术平方根等于它本身的绝对值.
知识梳理
如何区别 与 ?
从运算顺序看
从取值范围看
从运算结果看
先开方,后平方
先平方,后开方
a≥0
a取任何实数
a
|a|
意义
表示一个非负数a的算术平方根的平方
表示一个实数a的平方的算术平方根
知识梳理
积的算术平方根的性质:
商的算术平方根的性质:
即:
最简二次根式:
在根号内不含分母,不含开得尽方的因数或因式,这样的二次根式我们就说它是最简二次根式.
二次根式化简的结果应为最简二次根式。
对点训练
C
C
对点训练
D
B
知识梳理
知识点3 二次根式的运算
语言表述:算术平方根的积等于各个被开方数积的算术平方根.
二次根式的乘法法则:
二次根式相乘,__________不变,____________相乘.
根指数
被开方数
注意:a,b都必须是非负数.
反过来:
(a≥0,b≥0)
语言表述:积的算术平方根,等于积中各因式的算术平方根的积.
知识梳理
二次根式的乘法法则的推广:
①多个二次根式相乘时此法则也适用,即
②当二次根号外有因数(式)时,可以类比单项式乘单项式的法则计算,即根号外的因数(式)的积作为根号外的因数(式),被开方数的积作为被开方数,即
知识梳理
二次根式的除法法则:
算术平方根的商等于被开方数商的算术平方根.
当二次根式根号外的因数(式)不为1时,可类比单项式除以单项式法则,易得
知识梳理
商的算术平方根,等于积中各因式的算术平方根的商.
反过来,就得到
二次根式的商的算术平方根的性质:
知识梳理
二次根式的加减法法则:
一般地,二次根式加减时,可以先将二次根式化成最简二次根式,再将被开方数相同的二次根式进行合并.
(1)化——将非最简二次根式的二次根式化简;
加减法的运算步骤:
(2)找——找出被开方数相同的二次根式;
(3)并——把被开方数相同的二次根式合并.
一化简
二判断
三合并
依据:二次根式的性质、分配律和整式加减法则.
知识梳理
(1)二次根式混合运算的运算次序是:先乘除,后加减;
(2)整式运算的运算法则和运算律对二次根式同样适用。
(3)二次根式的运算结果能化简的必须化简。
二次根式的混合运算:
知识梳理
常见的乘法公式或法则:
(1)m(a+b+c)=_____________________;
(2)(x+a)(x+b)=_______________________;
(3)(a+b)(a-b)=_______________;
(4)(a±b)2=_______________________.
ma+mb+mc
x2+(a+b)x+ab
a2-b2
a2±2ab+b2
对点训练
B
6
D
对点训练
9
A
对点训练
6.计算:
知识梳理
知识点4 二次根式的应用
运用二次根式解决简单的实际问题时应注意的问题
1.读懂题意
2.分析解题思路
3.写出解题过程
对点训练
B
对点训练
提升训练
提升训练
Part 2
提升训练
C
A
提升训练
A
±1
提升训练
提升训练
C
提升训练
提升训练
提升训练
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
同课章节目录
- 第一章 二次根式
- 1.1 二次根式
- 1.2 二次根式的性质
- 1.3 二次根式的运算
- 第二章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程的应用
- 2.4 一元二次方程根与系数的关系(选学)
- 第三章 数据分析初步
- 3.1 平均数
- 3.2 中位数和众数
- 3.3 方差和标准差
- 第四章 平行四边形
- 4.1 多边形
- 4.2 平行四边形
- 4.3 中心对称
- 4.4 平行四边形的判定
- 4.5 三角形的中位线
- 4.6 反证法
- 第五章 特殊平行四边形
- 5.1 矩形
- 5.2 菱形
- 5.3 正方形
- 第六章 反比例函数
- 6.1 反比例函数
- 6.2 反比例函数的图象和性质
- 6.3 反比例函数的应用
