第二章 一元二次方程 章末复习 课件(共35张PPT)
文档属性
| 名称 | 第二章 一元二次方程 章末复习 课件(共35张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-05-24 11:23:55 | ||
图片预览











文档简介
(共35张PPT)
第二章 一元二次方程
章末复习课件
浙教版 八年级下册
知识梳理
知识梳理
Part 1
知识梳理
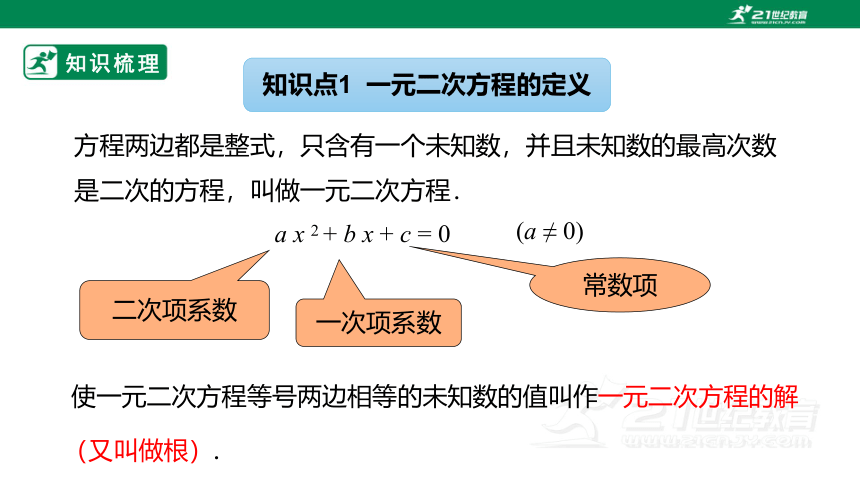
知识点1 一元二次方程的定义
方程两边都是整式,只含有一个未知数,并且未知数的最高次数是二次的方程,叫做一元二次方程.
a x 2 + b x + c = 0
(a ≠ 0)
二次项系数
一次项系数
常数项
使一元二次方程等号两边相等的未知数的值叫作一元二次方程的解(又叫做根).
对点训练
2.下列数:6,-6,8,-8,12,-12,2,-2,是方程x2-2x-48=0的根有( )
A.1个 B.2个 C.3个 D.4个
B
3.若关于x的方程 是一元二次方程,则此一元二次方程为 .
C
知识梳理
知识点2 一元二次方程的解法
因式分解法
对于一元二次方程,先因式分解使方程化为两个一次式的 等于0的形式,再使这两个一次式分别等于 ,从而实现 ,这种解法叫做因式分解法.
0
乘积
降次
知识梳理
1.移项:将方程化为一般形式,即方程右边化为 ;
2.分解:将方程的左边分解为两个一次式的 ;
3.转化:令每一个一次式分别为 ,得到两个一元一次方程;
0
0
乘积
简记歌诀:
右化零 左分解
两因式 各求解
4.求解:解这两个一元一次方程,它们的解就是原方程的解.
因式分解法的步骤
知识梳理
一般地,对于形如x2=a (a>0)的方程,根据平方根的定义,可解得 ,这种解一元二次方程的方法叫做开平方法.
直接开平方法解一元二次方程的“三步法”
开方
求解
变形
将方程化为含未知数的完全平方式=非负常 数的形式;
利用平方根的定义,将方程转化为两个一元一次方程;
解一元一次方程,得出方程的根.
直接开平方法
知识梳理
把一元二次方程的左边配成一个完全平方式,右边为一个非负常数,然后用开平方法求解,这种解一元二次方程的方法叫做配方法.
配方法解方程的步骤
①先化成 ;
一般形式
②将常数项移到等式右边;
③两边除以 ;
二次项系数
④方程两边都加上 ;
一次项系数一半的平方
⑤将等式左边化成 ;
完全平方形式
⑥两边开方,并求出方程的解.
配方法
知识梳理
公式法
一元二次方程ax2+bx+c=0(a≠0),当 时,
x= ,这个式子叫做一元二次方程ax2+bx+c=0的求根公式.
b2-4ac≥0
用公式法解一元二次方程的前提是:
1.必须是一般形式的一元二次方程: ax2+bx+c=0(a≠0).
2.b2-4ac≥0.
知识梳理
用公式法解一元二次方程的“四个步骤”:
(1) 把一元二次方程化为一般形式.
(2) 确定a,b,c的值.
(3) 计算b2-4ac的值.
(4) 当b2-4ac≥0时,把a,b,c的值代入求根公式,
求出方程的两个实数根;
当b2-4ac<0时,方程无实数根.
知识梳理
1.一般地,当一元二次方程一次项系数为0时(ax2+c=0),应选用直接开平方法;
2.若常数项为0( ax2+bx=0),应选用因式分解法;
3.若一次项系数和常数项都不为0 (ax2+bx+c=0),先化为一般式,看一边的整式是否容易因式分解,若容易,宜选用因式分解法,不然选用公式法;
4.当二次项系数是1,且一次项系数是偶数时,用配方法也较简单.
一元二次方程解法的选择
对点训练
1.若x2-2xy+y2=4,则x-y的值为( )
A.2 B.-2 C.±2 D.不能确定
C
2.把方程2x2+6x-1=0配方后得(x+m)2=k,则
m= ,k= .
3.关于x的一元二次方程x2+4x+k=0有两个相等的实根,则( )
A.k=-4 B.k=4 C.k≥-4 D.k≥4
B
对点训练
(1)2(x+3)2=8; (2)4x2- x+1=0;
【分析】方程一边以平方形式出现,另一边是常数,可直接开平方法.
解:开平方,得
x + 3 = ±2.
解得, x 1= -1 , x2=-5
【分析】二次项的系数为偶数,可用配方法来解题较快.
解:配方,得
开平方,得
解得,
4.解下列一元二次方程:
对点训练
(3)(3x-4)2=9x-12; (4)x2-2x-99=0.
【分析】方程左右两边可以提取公因式,所以用因式分解法解答较快.
解:移项,得
(3x-4)2-(9x-12)=0
因式分解,得
(3x-4)(3x-7)=0
即:3x-4=0或3x-7=0
【分析】二次项系数为1,一次项系数为偶数,可用配方法.
解:配方,得
(x-1)2=100
开平方,得
(x-1)=±10
解得:x1=11,x2=-9
知识梳理
知识点3 一元二次方程的应用
列一元二次方程解应用题的基本步骤
审
设
列
解
检
答
(1)审题:理解题意,分清有哪些已知量、未知量
(2)设元(未知数)。
(3)寻找相等关系,列方程。
(4)解方程
(5)检验根的准确性及是否符合实际意义。
(6)作答
对点训练
C
20%
对点训练
D
对点训练
B
7
知识梳理
知识点4 一元二次方程根与系数的关系
一般的,一元二次方程的根与系数有如下关系:
如果x1,x2是一元二次方程 ax2+bx+c=0 的两个根,那么
x1+x2= ,x1·x2=
两个根的和等于一次项系数与二次项系数的比的相反数,
两个根的积等于常数项与二次项系数的比.
【特别强调】满足上述关系的前提条件:b2-4ac≥0.
对点训练
D
D
对点训练
提升训练
提升训练
Part 2
提升训练
1.若实数a,b满足(a2+b2-3)2=25,则a2+b2的值为( )
A.8 B.8或-2 C.-2 D.28
A
2.若关于x的一元二次方程x2-4x-m=0有两个不相等的实数根,则实数m的取值范围是 .
m>-4
3.设一元二次方程x2-7x+3=0的两根为x1,x2,则x1+x2= ,x1x2= ,(x1-2)(x2-2)= .
7
3
-7
提升训练
x≥4
B
C
提升训练
提升训练
8.试证明:无论a为何实数,关于x的方程(a2-8a+17)x2+2ax+1=0都是一元二次方程.
证明:∵a2-8a+17=(a-4)2+1>0,
∴无论a为何实数,该方程都是一元二次方程.
提升训练
提升训练
提升训练
提升训练
提升训练
提升训练
提升训练
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
第二章 一元二次方程
章末复习课件
浙教版 八年级下册
知识梳理
知识梳理
Part 1
知识梳理
知识点1 一元二次方程的定义
方程两边都是整式,只含有一个未知数,并且未知数的最高次数是二次的方程,叫做一元二次方程.
a x 2 + b x + c = 0
(a ≠ 0)
二次项系数
一次项系数
常数项
使一元二次方程等号两边相等的未知数的值叫作一元二次方程的解(又叫做根).
对点训练
2.下列数:6,-6,8,-8,12,-12,2,-2,是方程x2-2x-48=0的根有( )
A.1个 B.2个 C.3个 D.4个
B
3.若关于x的方程 是一元二次方程,则此一元二次方程为 .
C
知识梳理
知识点2 一元二次方程的解法
因式分解法
对于一元二次方程,先因式分解使方程化为两个一次式的 等于0的形式,再使这两个一次式分别等于 ,从而实现 ,这种解法叫做因式分解法.
0
乘积
降次
知识梳理
1.移项:将方程化为一般形式,即方程右边化为 ;
2.分解:将方程的左边分解为两个一次式的 ;
3.转化:令每一个一次式分别为 ,得到两个一元一次方程;
0
0
乘积
简记歌诀:
右化零 左分解
两因式 各求解
4.求解:解这两个一元一次方程,它们的解就是原方程的解.
因式分解法的步骤
知识梳理
一般地,对于形如x2=a (a>0)的方程,根据平方根的定义,可解得 ,这种解一元二次方程的方法叫做开平方法.
直接开平方法解一元二次方程的“三步法”
开方
求解
变形
将方程化为含未知数的完全平方式=非负常 数的形式;
利用平方根的定义,将方程转化为两个一元一次方程;
解一元一次方程,得出方程的根.
直接开平方法
知识梳理
把一元二次方程的左边配成一个完全平方式,右边为一个非负常数,然后用开平方法求解,这种解一元二次方程的方法叫做配方法.
配方法解方程的步骤
①先化成 ;
一般形式
②将常数项移到等式右边;
③两边除以 ;
二次项系数
④方程两边都加上 ;
一次项系数一半的平方
⑤将等式左边化成 ;
完全平方形式
⑥两边开方,并求出方程的解.
配方法
知识梳理
公式法
一元二次方程ax2+bx+c=0(a≠0),当 时,
x= ,这个式子叫做一元二次方程ax2+bx+c=0的求根公式.
b2-4ac≥0
用公式法解一元二次方程的前提是:
1.必须是一般形式的一元二次方程: ax2+bx+c=0(a≠0).
2.b2-4ac≥0.
知识梳理
用公式法解一元二次方程的“四个步骤”:
(1) 把一元二次方程化为一般形式.
(2) 确定a,b,c的值.
(3) 计算b2-4ac的值.
(4) 当b2-4ac≥0时,把a,b,c的值代入求根公式,
求出方程的两个实数根;
当b2-4ac<0时,方程无实数根.
知识梳理
1.一般地,当一元二次方程一次项系数为0时(ax2+c=0),应选用直接开平方法;
2.若常数项为0( ax2+bx=0),应选用因式分解法;
3.若一次项系数和常数项都不为0 (ax2+bx+c=0),先化为一般式,看一边的整式是否容易因式分解,若容易,宜选用因式分解法,不然选用公式法;
4.当二次项系数是1,且一次项系数是偶数时,用配方法也较简单.
一元二次方程解法的选择
对点训练
1.若x2-2xy+y2=4,则x-y的值为( )
A.2 B.-2 C.±2 D.不能确定
C
2.把方程2x2+6x-1=0配方后得(x+m)2=k,则
m= ,k= .
3.关于x的一元二次方程x2+4x+k=0有两个相等的实根,则( )
A.k=-4 B.k=4 C.k≥-4 D.k≥4
B
对点训练
(1)2(x+3)2=8; (2)4x2- x+1=0;
【分析】方程一边以平方形式出现,另一边是常数,可直接开平方法.
解:开平方,得
x + 3 = ±2.
解得, x 1= -1 , x2=-5
【分析】二次项的系数为偶数,可用配方法来解题较快.
解:配方,得
开平方,得
解得,
4.解下列一元二次方程:
对点训练
(3)(3x-4)2=9x-12; (4)x2-2x-99=0.
【分析】方程左右两边可以提取公因式,所以用因式分解法解答较快.
解:移项,得
(3x-4)2-(9x-12)=0
因式分解,得
(3x-4)(3x-7)=0
即:3x-4=0或3x-7=0
【分析】二次项系数为1,一次项系数为偶数,可用配方法.
解:配方,得
(x-1)2=100
开平方,得
(x-1)=±10
解得:x1=11,x2=-9
知识梳理
知识点3 一元二次方程的应用
列一元二次方程解应用题的基本步骤
审
设
列
解
检
答
(1)审题:理解题意,分清有哪些已知量、未知量
(2)设元(未知数)。
(3)寻找相等关系,列方程。
(4)解方程
(5)检验根的准确性及是否符合实际意义。
(6)作答
对点训练
C
20%
对点训练
D
对点训练
B
7
知识梳理
知识点4 一元二次方程根与系数的关系
一般的,一元二次方程的根与系数有如下关系:
如果x1,x2是一元二次方程 ax2+bx+c=0 的两个根,那么
x1+x2= ,x1·x2=
两个根的和等于一次项系数与二次项系数的比的相反数,
两个根的积等于常数项与二次项系数的比.
【特别强调】满足上述关系的前提条件:b2-4ac≥0.
对点训练
D
D
对点训练
提升训练
提升训练
Part 2
提升训练
1.若实数a,b满足(a2+b2-3)2=25,则a2+b2的值为( )
A.8 B.8或-2 C.-2 D.28
A
2.若关于x的一元二次方程x2-4x-m=0有两个不相等的实数根,则实数m的取值范围是 .
m>-4
3.设一元二次方程x2-7x+3=0的两根为x1,x2,则x1+x2= ,x1x2= ,(x1-2)(x2-2)= .
7
3
-7
提升训练
x≥4
B
C
提升训练
提升训练
8.试证明:无论a为何实数,关于x的方程(a2-8a+17)x2+2ax+1=0都是一元二次方程.
证明:∵a2-8a+17=(a-4)2+1>0,
∴无论a为何实数,该方程都是一元二次方程.
提升训练
提升训练
提升训练
提升训练
提升训练
提升训练
提升训练
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
同课章节目录
- 第一章 二次根式
- 1.1 二次根式
- 1.2 二次根式的性质
- 1.3 二次根式的运算
- 第二章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程的应用
- 2.4 一元二次方程根与系数的关系(选学)
- 第三章 数据分析初步
- 3.1 平均数
- 3.2 中位数和众数
- 3.3 方差和标准差
- 第四章 平行四边形
- 4.1 多边形
- 4.2 平行四边形
- 4.3 中心对称
- 4.4 平行四边形的判定
- 4.5 三角形的中位线
- 4.6 反证法
- 第五章 特殊平行四边形
- 5.1 矩形
- 5.2 菱形
- 5.3 正方形
- 第六章 反比例函数
- 6.1 反比例函数
- 6.2 反比例函数的图象和性质
- 6.3 反比例函数的应用
