6.1矩形（1）

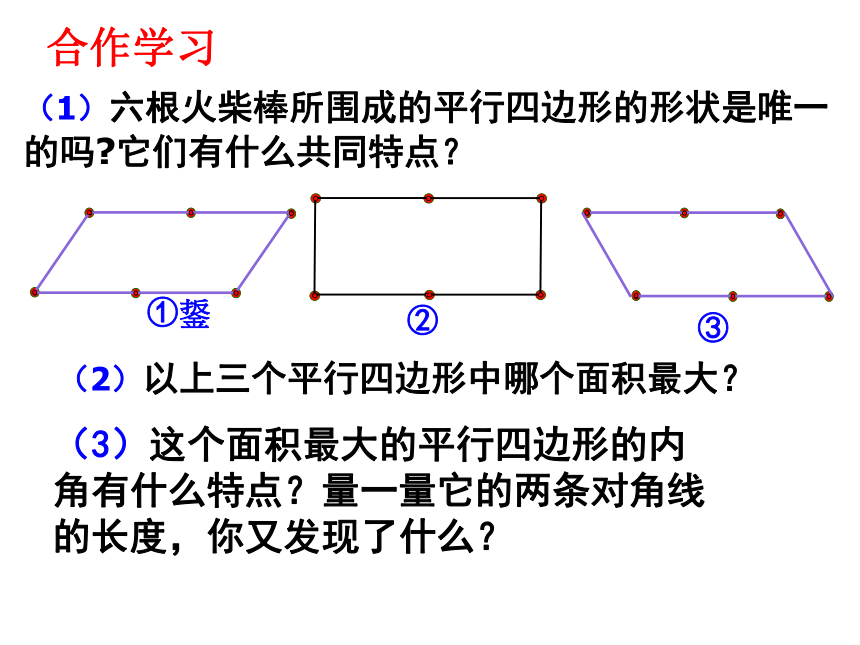
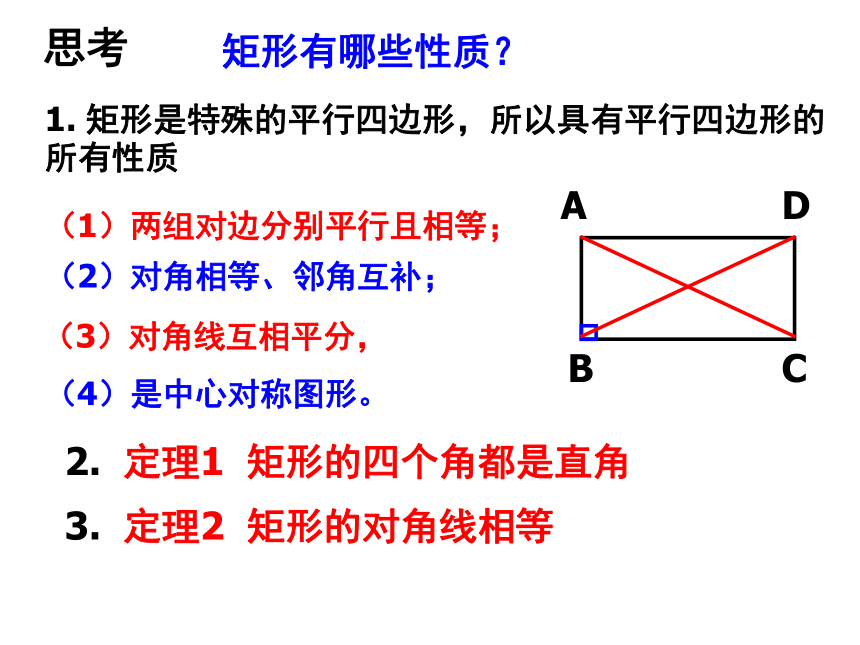
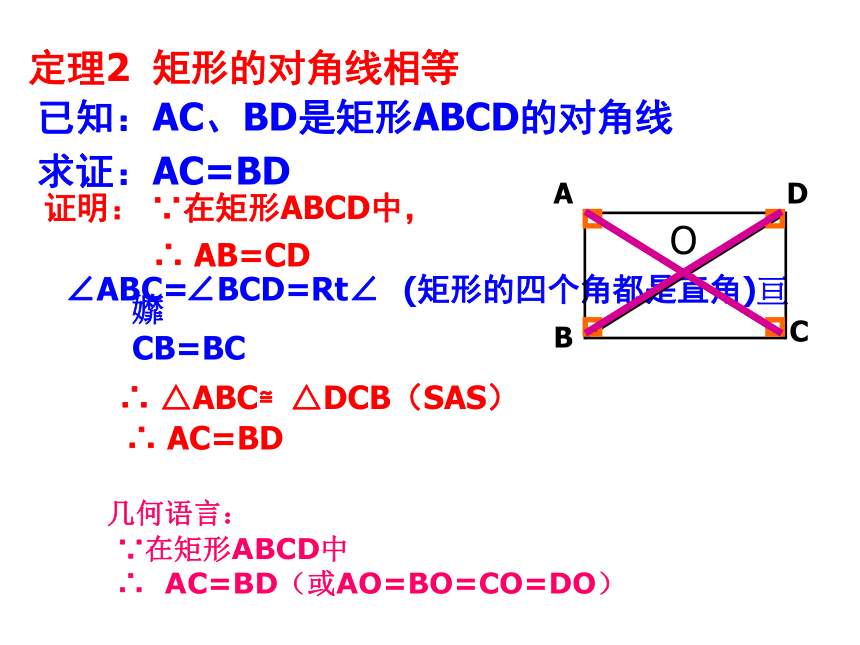
课件19张PPT。6.1 矩形 (1)（1）六根火柴棒所围成的平行四边形的形状是唯一的吗?它们有什么共同特点？（2）以上三个平行四边形中哪个面积最大？ 合作学习（3）这个面积最大的平行四边形的内角有什么特点？量一量它的两条对角线的长度，你又发现了什么？矩形：有一个角是直角的平行四边形矩形：矩形的表示方法: 矩形ABCD矩形定义：小学学过的长方形、正方形都是矩形。矩形有哪些性质？思考 （1）两组对边分别平行且相等；（2）对角相等、邻角互补；（3）对角线互相平分，（4）是中心对称图形。1. 矩形是特殊的平行四边形，所以具有平行四边形的所有性质2. 定理1 矩形的四个角都是直角 3. 定理2 矩形的对角线相等 ABCD定理2 矩形的对角线相等 已知：AC、BD是矩形ABCD的对角线求证：AC=BD证明： ∵在矩形ABCD中，∴ AB=CD?CB=BC∴ △ABC≌△DCB（SAS） ∴ AC=BD 几何语言：
∵在矩形ABCD中
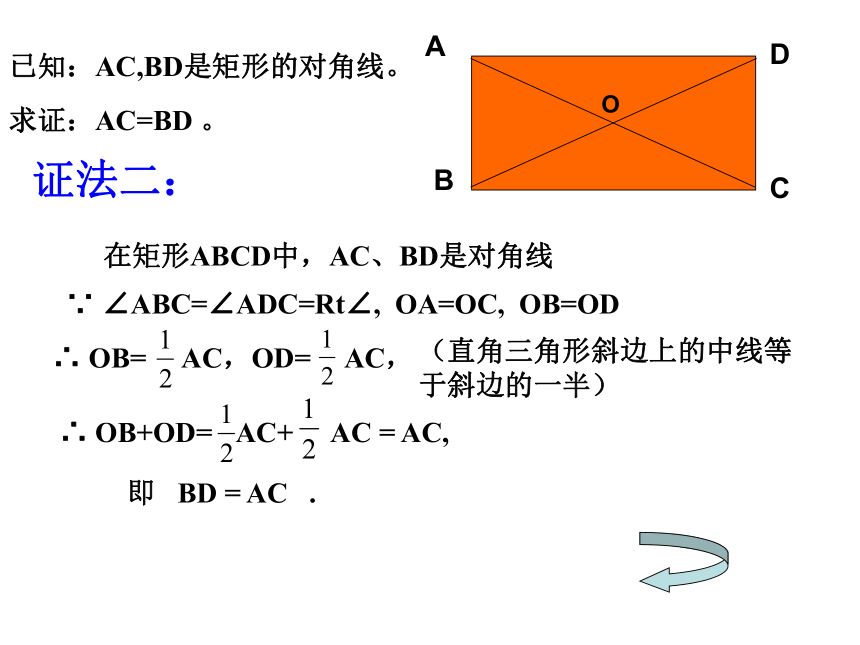
∴ AC=BD（或AO=BO=CO=DO）证法二：O已知：AC,BD是矩形的对角线。求证：AC=BD 。 在矩形ABCD中，AC、BD是对角线即 BD = AC .∵ ∠ABC=∠ADC=Rt∠, OA=OC, OB=OD课内练习1.
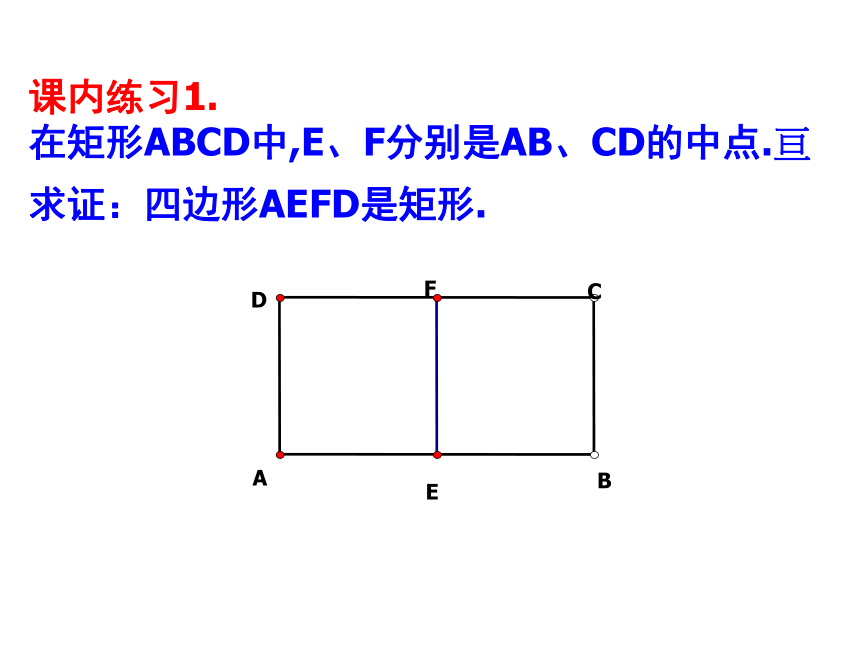
在矩形ABCD中,E、F分别是AB、CD的中点.?求证：四边形AEFD是矩形.课内练习2：1.矩形ABCD，对角线AC、BD相交于点O，
图中①有多少个直角三角形，多少个等腰三角形？②有多少对全等三角形？例1：已知：如图，在矩形ABCD中对角线AC、BD相交于点O，∠AOD=120°，AB=4cm。(1)判断△AOB的形状；(2)求对角线的长； (3)作∠BAO的平分线，交BC于E，连结OE
求证：OE⊥AC E (4)延长EO，与AD交于F， 问：△AEF是什么三角形？ F 变式ABCDO矩形的对称性:矩形是中心对称图形,又是轴对称图形。矩形的对称中心在哪？矩形是对称轴有几条?1.已知矩形ABCD的周长是14cm，
相邻两边的差是1cm，
求（1）矩形ABCD的面积是多少?12cm2 3或4cm （2）AB的长？ 巩固练习（3）BO的长？ 2.5cm 2、已知:如图,过矩形ABCD的顶点C作CE//BD，交AB的延长线于E。 求证：∠CAE=∠CEA本节课你学到什么？1.一个定义：2.二个定理:3.二个结论:(1)矩形的两条对角线被交点分成的四条线段 相等(2)矩形既是轴对称图形，又是中心对称图形这节课你学到了什么? 还有什么困惑吗？ 1、已知:如图,在矩形ABCD中, 对角线相交于点O,
∠AOB=60°,AE平分∠BAD,AE交BC于E,求∠BOE的度数.75°运用性质，提高能力ABCDEF 2、 矩形ABCD，折叠矩形的一边AD，使D点落在BC边上的点F处，已知AB=8，BC=10，求：EC的长运用性质，提高能力若要使∠AMD是直角，应增加什么条件？拓展2（1）判断如图5X5方格内四边形ABCD是不是
矩形，说明理由；
（2）以DE为一边作一个矩形，要求另外两个
顶点也在方格顶点上。ABCD 变式：已知如图，矩形OABC的长为 ，宽OC 为1，将⊿AOC沿AC翻折得⊿ APC．求：（1）∠PCB的度数
（2）点P的坐标
挑战中考翻折全等相等的边，相等的角