第六章 反比例函数 章末复习 课件(共32张PPT)
文档属性
| 名称 | 第六章 反比例函数 章末复习 课件(共32张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-05-24 00:00:00 | ||
图片预览









文档简介
(共32张PPT)
第六章 反比例函数
章末复习
浙教版 八年级下册
其中x是自变量,y是x的函数,k是比例系数.
一般地,形如 (k是常数,k≠0)的函数叫做反比例函数.
注意:自变量x的取值范围,
(1)因为 x 作为分母,不能等于零,因此自变量 x 的取值范围是所有非零实数.
(2)在实际问题中自变量x的取值范围要根据具体情况来确定.
反比例函数的定义:
知识梳理
反比例函数的表达形式:
① (k≠0)
②xy=k(k≠0)
③y=kx-1(k≠0)
x≠0,y≠0
知识梳理
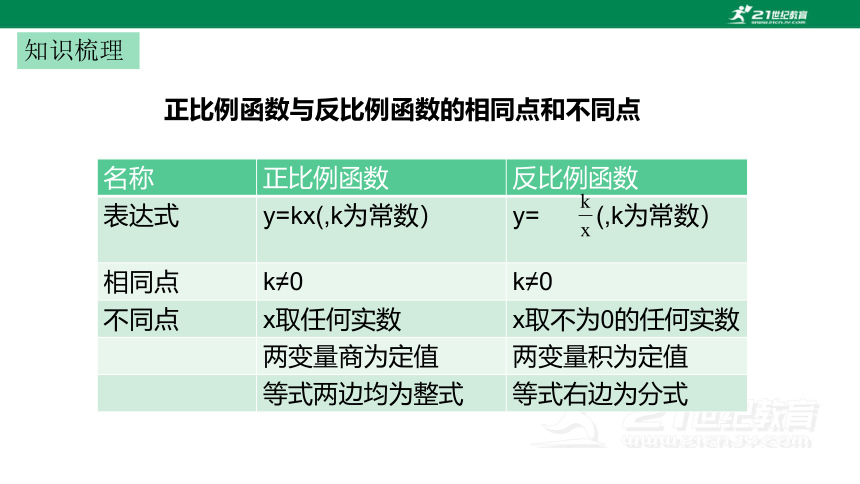
正比例函数与反比例函数的相同点和不同点
名称 正比例函数 反比例函数
表达式 y=kx(,k为常数) y= (,k为常数)
相同点 k≠0 k≠0
不同点 x取任何实数 x取不为0的任何实数
两变量商为定值 两变量积为定值
等式两边均为整式 等式右边为分式
知识梳理
用待定系数法确定反比例函数的表达式的一般步骤:
二 代
三 求
四 写
一 设
设反比例函数
将一对对应的x,y值带入函数,得到关于k的方程
解方程求待定系数k
写出反比例函数表达式
用待定系数法求反比例函数解析式,只需x,y的一对值即可,k ≠ 0.
知识梳理
1.下列函数中反比例函数有( )
A.1个 B.2个 C.3个 D.4个
C
2.若y=(m-1)xm2-2是反比例函数,则m=____,此函数的解析式是_____________.
-1
(k为常数,k≠0)
对点训练
3.已知y与x-1成反比例,且当x= 时,y=- .
(1)求 y关于x的函数解析式;
(2)当 y= 时,求x的值.
解:(1)设y关于x的函数解析式为
即y关于x的函数解析式为
对点训练
反比例函数 的图象是由两个分支组成的曲线。
当k>0时,两支曲线分别位于_______________内;
当k<0时,两支曲线分别位于_______________内.
第一、三象限
第二、四象限
图象关于直角坐标系的原点成中心对称.
反比例函数的图象为双曲线.
反比例函数的图象与性质:
知识梳理
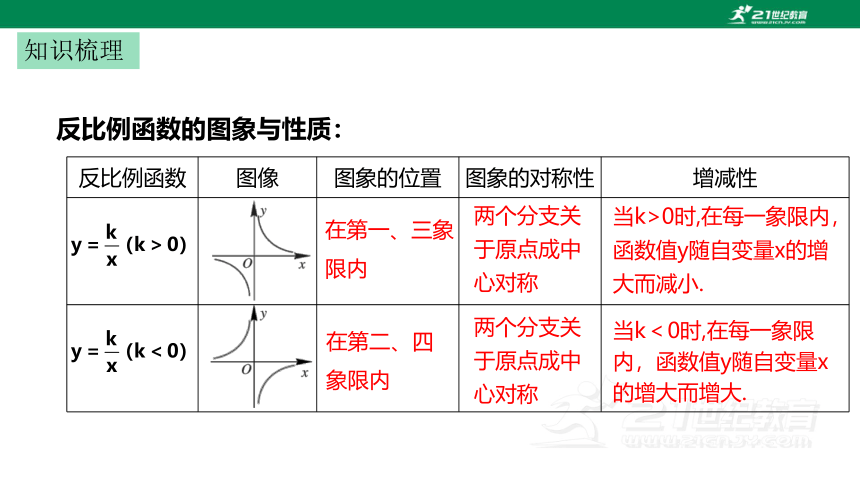
反比例函数 图像 图象的位置 图象的对称性 增减性
在第一、三象限内
在第二、四象限内
两个分支关于原点成中心对称
两个分支关于原点成中心对称
当k>0时,在每一象限内,函数值y随自变量x的增大而减小.
当k<0时,在每一象限内,函数值y随自变量x的增大而增大.
反比例函数的图象与性质:
知识梳理
1.已知点P(1,-3)在反比例函数y= (k≠0)的图象上,则k的值是( )
A.3 B.-3 C.13 D.-13
B
2.已知点A(1,y1),B(2,y2),C(-3,y3)都在反比例函数y= 的图象上,则y1,y2,y3的大小关系是( )
A.y3<y1<y2 B.y1<y2<y3
C.y2<y1<y3 D.y3<y2<y1
D
对点训练
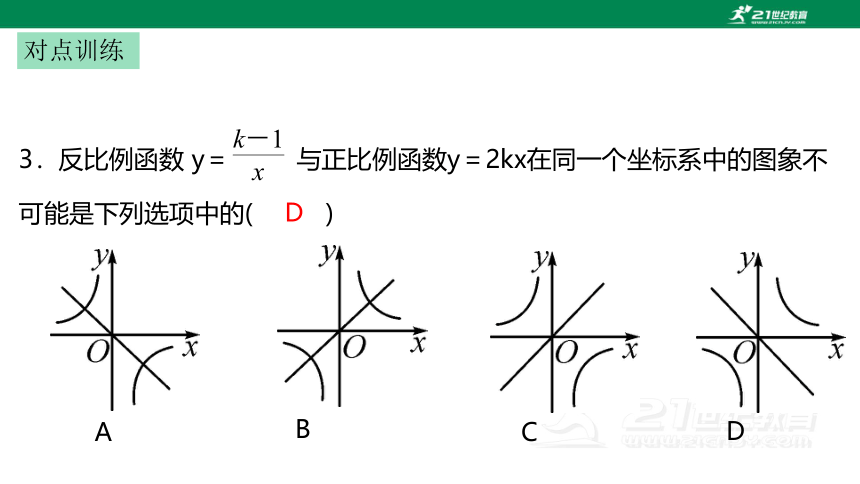
3.反比例函数 y= 与正比例函数y=2kx在同一个坐标系中的图象不可能是下列选项中的( )
A
B
C
D
D
对点训练
4.如图,双曲线 y= 与直线 y=- x 交于A,B两点,且点A(-2,m),则点B的坐标是( )
A.(2,-1) B.(1,-2)
A
对点训练
5.已知一次函数 y=x-b与反比例函数 y= 的图象有一个交点的纵坐标是2,则b的值为______.
6.已知反比例函数 的图象在其所在的象限内,y随x的增大而减小,求k的值.
由①,得k>3,由②,得k=± ,综合①②得k= .
-1
对点训练
反比例函数中比例系数k的几何意义
若点P是 图象上的任意一点,作PA垂直于x轴,作PB垂直于y轴,矩形AOBP的面积与k的关系是S矩形 AOBP=|k|.
y
x
O
P
A
B
B
P
A
知识梳理
点Q是其图象上的任意一点,作QA垂直于y轴,作QB垂直于x轴,矩形AOBQ的面积与k的关系是S矩形 AOBQ=|k|
结论:△QAO与△QBO的面积和k的关系是S△QAO=S△QBO=
Q
对于反比例函数 ,
A
B
y
x
O
知识梳理
1.如图,两个反比例函数y= 和y= 在第一象限内的图象分别是C1和C2,设点P在C1上,PA⊥x轴于点A,交C2于点B,则△POB的面积为________.
1
对点训练
2 .如图,点A在双曲线y= 上,点B在双曲线y= 上,且AB∥x轴,C,D在x轴上,若四边形ABCD为矩形,则它的面积为________.
2
对点训练
反比例函数应用的常用解题思路是:
(1)根据题意确定反比例函数关系式:
(2)由反比例关系式及题中条件去解决实际问题
1.审题、准确判断数量关系
反比例函数应用一般解题步骤:
2.建立反比例函数的模型
3.根据实际情况确定自变量的取值范围
4.实际问题的求解
知识梳理
1.一台印刷机每年可印刷的书本数量 y(万册)与它的使用时间x(年)成反比例关系,当x=2时,y=20.则y与x的函数图象大致是( )
A
B
C
D
C
对点训练
2.如图是汽车在某高速公路上匀速行驶时,速度v(km/h)与行驶时间t(h)的函数图象.请根据图象提供的信息回答问题:汽车最慢用____h可以到达;如果要在4 h内到达,汽车的速度应不低于____km/h.
6
75
对点训练
3.如图,已知反比例函数 y= 的图象的一支位于第一象限.
(1)判断该函数图象的另一支所在的象限,并求m的取值范围;
(2)O为坐标原点,点A在该反比例函数位于第一象限的图象上,点B与点A关于x轴对称,若△OAB的面积为6,求m的值.
解:(1)根据反比例函数的图象关于原点对称知,该函数图象的另一支在第三象限,且m-7>0,则m>7;
对点训练
(2)设线段AB交x轴于点C.
∵点B与点A关于x轴对称,若△OAB的面积为6, 则△OAC的面积为3,
∴ (m-7)=3,
∴m=13.
对点训练
4.某气球内充满了一定质量的气体,当温度不变时,气球内气体的气压p(kPa)是气球的体积V(m3)的反比例函数,其图象如图所示.(kPa是一种压强单位)
(1)写出这个函数的解析式;
(2)当气球的体积为0.8 m3时,气球内的气压是多少千帕?
(3)当气球内气压大于144 kPa时,气球将爆炸,为了安全起见,气球的体积应不小于多少立方米?
对点训练
(2)120 kPa;
(3)当p=144 kPa时,V= m3.根据函数图象得,当p≤144 kPa时,
V≥ m3.
∴为了安全起见,气球的体积应不小于 m3.
对点训练
提升训练
提升训练
提升训练
提升训练
提升训练
提升训练
提升训练
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
第六章 反比例函数
章末复习
浙教版 八年级下册
其中x是自变量,y是x的函数,k是比例系数.
一般地,形如 (k是常数,k≠0)的函数叫做反比例函数.
注意:自变量x的取值范围,
(1)因为 x 作为分母,不能等于零,因此自变量 x 的取值范围是所有非零实数.
(2)在实际问题中自变量x的取值范围要根据具体情况来确定.
反比例函数的定义:
知识梳理
反比例函数的表达形式:
① (k≠0)
②xy=k(k≠0)
③y=kx-1(k≠0)
x≠0,y≠0
知识梳理
正比例函数与反比例函数的相同点和不同点
名称 正比例函数 反比例函数
表达式 y=kx(,k为常数) y= (,k为常数)
相同点 k≠0 k≠0
不同点 x取任何实数 x取不为0的任何实数
两变量商为定值 两变量积为定值
等式两边均为整式 等式右边为分式
知识梳理
用待定系数法确定反比例函数的表达式的一般步骤:
二 代
三 求
四 写
一 设
设反比例函数
将一对对应的x,y值带入函数,得到关于k的方程
解方程求待定系数k
写出反比例函数表达式
用待定系数法求反比例函数解析式,只需x,y的一对值即可,k ≠ 0.
知识梳理
1.下列函数中反比例函数有( )
A.1个 B.2个 C.3个 D.4个
C
2.若y=(m-1)xm2-2是反比例函数,则m=____,此函数的解析式是_____________.
-1
(k为常数,k≠0)
对点训练
3.已知y与x-1成反比例,且当x= 时,y=- .
(1)求 y关于x的函数解析式;
(2)当 y= 时,求x的值.
解:(1)设y关于x的函数解析式为
即y关于x的函数解析式为
对点训练
反比例函数 的图象是由两个分支组成的曲线。
当k>0时,两支曲线分别位于_______________内;
当k<0时,两支曲线分别位于_______________内.
第一、三象限
第二、四象限
图象关于直角坐标系的原点成中心对称.
反比例函数的图象为双曲线.
反比例函数的图象与性质:
知识梳理
反比例函数 图像 图象的位置 图象的对称性 增减性
在第一、三象限内
在第二、四象限内
两个分支关于原点成中心对称
两个分支关于原点成中心对称
当k>0时,在每一象限内,函数值y随自变量x的增大而减小.
当k<0时,在每一象限内,函数值y随自变量x的增大而增大.
反比例函数的图象与性质:
知识梳理
1.已知点P(1,-3)在反比例函数y= (k≠0)的图象上,则k的值是( )
A.3 B.-3 C.13 D.-13
B
2.已知点A(1,y1),B(2,y2),C(-3,y3)都在反比例函数y= 的图象上,则y1,y2,y3的大小关系是( )
A.y3<y1<y2 B.y1<y2<y3
C.y2<y1<y3 D.y3<y2<y1
D
对点训练
3.反比例函数 y= 与正比例函数y=2kx在同一个坐标系中的图象不可能是下列选项中的( )
A
B
C
D
D
对点训练
4.如图,双曲线 y= 与直线 y=- x 交于A,B两点,且点A(-2,m),则点B的坐标是( )
A.(2,-1) B.(1,-2)
A
对点训练
5.已知一次函数 y=x-b与反比例函数 y= 的图象有一个交点的纵坐标是2,则b的值为______.
6.已知反比例函数 的图象在其所在的象限内,y随x的增大而减小,求k的值.
由①,得k>3,由②,得k=± ,综合①②得k= .
-1
对点训练
反比例函数中比例系数k的几何意义
若点P是 图象上的任意一点,作PA垂直于x轴,作PB垂直于y轴,矩形AOBP的面积与k的关系是S矩形 AOBP=|k|.
y
x
O
P
A
B
B
P
A
知识梳理
点Q是其图象上的任意一点,作QA垂直于y轴,作QB垂直于x轴,矩形AOBQ的面积与k的关系是S矩形 AOBQ=|k|
结论:△QAO与△QBO的面积和k的关系是S△QAO=S△QBO=
Q
对于反比例函数 ,
A
B
y
x
O
知识梳理
1.如图,两个反比例函数y= 和y= 在第一象限内的图象分别是C1和C2,设点P在C1上,PA⊥x轴于点A,交C2于点B,则△POB的面积为________.
1
对点训练
2 .如图,点A在双曲线y= 上,点B在双曲线y= 上,且AB∥x轴,C,D在x轴上,若四边形ABCD为矩形,则它的面积为________.
2
对点训练
反比例函数应用的常用解题思路是:
(1)根据题意确定反比例函数关系式:
(2)由反比例关系式及题中条件去解决实际问题
1.审题、准确判断数量关系
反比例函数应用一般解题步骤:
2.建立反比例函数的模型
3.根据实际情况确定自变量的取值范围
4.实际问题的求解
知识梳理
1.一台印刷机每年可印刷的书本数量 y(万册)与它的使用时间x(年)成反比例关系,当x=2时,y=20.则y与x的函数图象大致是( )
A
B
C
D
C
对点训练
2.如图是汽车在某高速公路上匀速行驶时,速度v(km/h)与行驶时间t(h)的函数图象.请根据图象提供的信息回答问题:汽车最慢用____h可以到达;如果要在4 h内到达,汽车的速度应不低于____km/h.
6
75
对点训练
3.如图,已知反比例函数 y= 的图象的一支位于第一象限.
(1)判断该函数图象的另一支所在的象限,并求m的取值范围;
(2)O为坐标原点,点A在该反比例函数位于第一象限的图象上,点B与点A关于x轴对称,若△OAB的面积为6,求m的值.
解:(1)根据反比例函数的图象关于原点对称知,该函数图象的另一支在第三象限,且m-7>0,则m>7;
对点训练
(2)设线段AB交x轴于点C.
∵点B与点A关于x轴对称,若△OAB的面积为6, 则△OAC的面积为3,
∴ (m-7)=3,
∴m=13.
对点训练
4.某气球内充满了一定质量的气体,当温度不变时,气球内气体的气压p(kPa)是气球的体积V(m3)的反比例函数,其图象如图所示.(kPa是一种压强单位)
(1)写出这个函数的解析式;
(2)当气球的体积为0.8 m3时,气球内的气压是多少千帕?
(3)当气球内气压大于144 kPa时,气球将爆炸,为了安全起见,气球的体积应不小于多少立方米?
对点训练
(2)120 kPa;
(3)当p=144 kPa时,V= m3.根据函数图象得,当p≤144 kPa时,
V≥ m3.
∴为了安全起见,气球的体积应不小于 m3.
对点训练
提升训练
提升训练
提升训练
提升训练
提升训练
提升训练
提升训练
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
同课章节目录
- 第一章 二次根式
- 1.1 二次根式
- 1.2 二次根式的性质
- 1.3 二次根式的运算
- 第二章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程的应用
- 2.4 一元二次方程根与系数的关系(选学)
- 第三章 数据分析初步
- 3.1 平均数
- 3.2 中位数和众数
- 3.3 方差和标准差
- 第四章 平行四边形
- 4.1 多边形
- 4.2 平行四边形
- 4.3 中心对称
- 4.4 平行四边形的判定
- 4.5 三角形的中位线
- 4.6 反证法
- 第五章 特殊平行四边形
- 5.1 矩形
- 5.2 菱形
- 5.3 正方形
- 第六章 反比例函数
- 6.1 反比例函数
- 6.2 反比例函数的图象和性质
- 6.3 反比例函数的应用
