第五章 特殊平行四边形 章末复习课件(共28张PPT)
文档属性
| 名称 | 第五章 特殊平行四边形 章末复习课件(共28张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-05-24 11:23:55 | ||
图片预览





文档简介
(共28张PPT)
第五章 特殊平行四边形
章末复习
浙教版 八年级下册
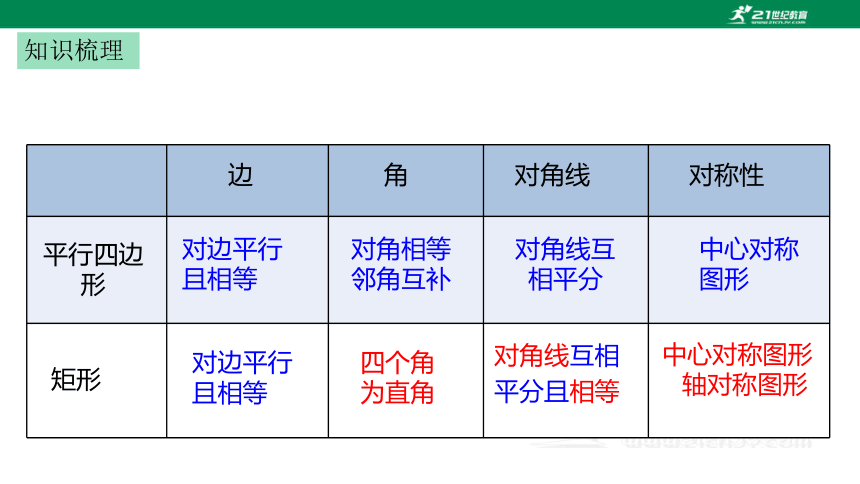
知识梳理
矩形的性质及判定
1.定义:有一个角是直角的平行四边形叫做矩形.也叫做长方形.
矩形是特殊的平行四边形.
矩形除了具有平行四边形所有性质,还具有的性质有:
矩形的对角线相等
2.矩形的性质:
矩形的四个角都是直角
边
角
对角线
对称性
平行四边形
矩形
对边平行
且相等
对角相等
邻角互补
对角线互
相平分
中心对称图形
对边平行
且相等
四个角
为直角
对角线互相
平分且相等
中心对称图形
轴对称图形
知识梳理
有一个角是直角的平行四边形是矩形.
对角线相等的平行四边形是矩形 .
(对角线相等且互相平分的四边形是矩形.)
有三个角是直角的四边形是矩形 .
方法1:
方法2:
方法3:
3.矩形的判定:
知识梳理
1.在矩形ABCD中,O是BC的中点,∠AOD=90°,矩形ABCD的周长为24 cm,则AB的长为( )
A.1 cm B.2 cm C.2.5 cm D.4 cm
D
2.四边形ABCD的对角线AC,BD相交于点O,已知下列6个条件:①AB∥DC;②AB=DC;③AC=BD;④∠ABC=90°;⑤OA=OC;⑥OB=OD.能判定四边形ABCD是矩形的有_____________________________________.(填序号)
①②③(或①②④或③⑤⑥或④⑤⑥)
对点训练
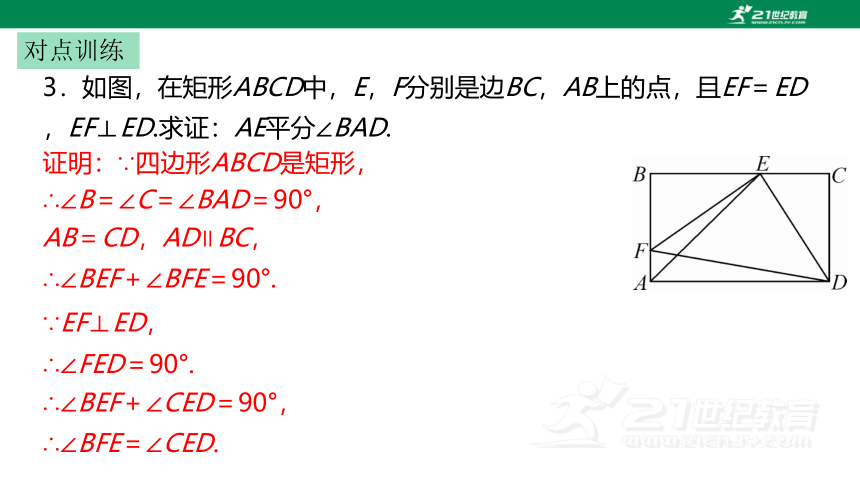
3.如图,在矩形ABCD中,E,F分别是边BC,AB上的点,且EF=ED,EF⊥ED.求证:AE平分∠BAD.
证明:∵四边形ABCD是矩形,
∴∠B=∠C=∠BAD=90°,
AB=CD,AD∥BC,
∴∠BEF+∠BFE=90°.
∵EF⊥ED,
∴∠FED=90°.
∴∠BEF+∠CED=90°,
∴∠BFE=∠CED.
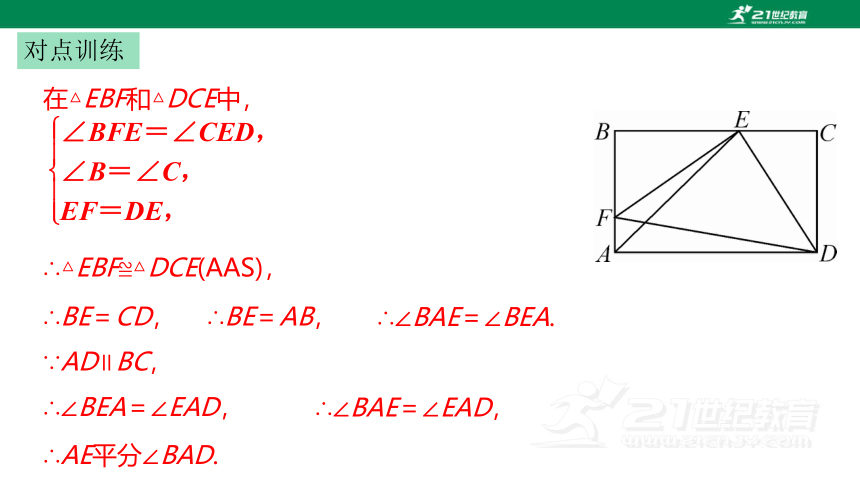
对点训练
∴△EBF≌△DCE(AAS),
在△EBF和△DCE中,
∴BE=CD,
∵AD∥BC,
∴∠BEA=∠EAD,
∴AE平分∠BAD.
∴BE=AB,
∴∠BAE=∠BEA.
∴∠BAE=∠EAD,
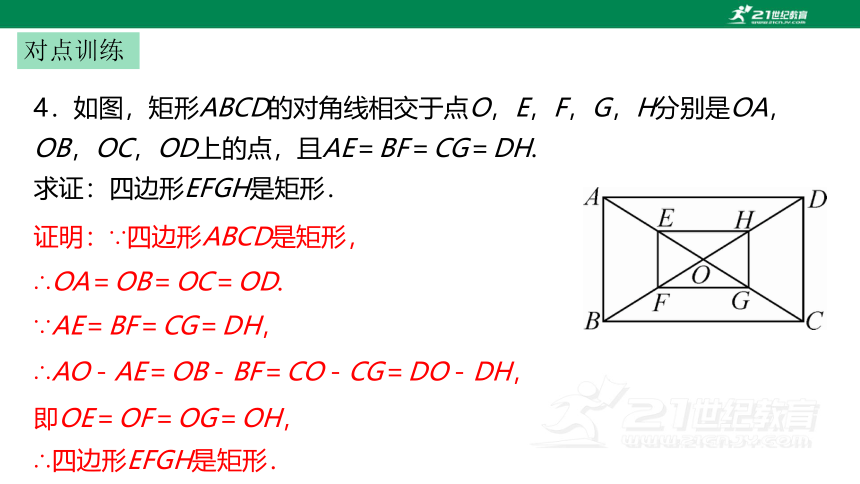
对点训练
4.如图,矩形ABCD的对角线相交于点O,E,F,G,H分别是OA,OB,OC,OD上的点,且AE=BF=CG=DH.
求证:四边形EFGH是矩形.
证明:∵四边形ABCD是矩形,
∴OA=OB=OC=OD.
∵AE=BF=CG=DH,
∴AO-AE=OB-BF=CO-CG=DO-DH,
即OE=OF=OG=OH,
∴四边形EFGH是矩形.
对点训练
菱形的性质及判定
1.定义:有一组邻边相等的平行四边形叫做菱形.
菱形是特殊的平行四边形.
菱形除了具有平行四边形所有性质,还具有的性质有:
2.菱形的性质:
菱形的四条边都相等
菱形的两条对角线互相垂直,并且每一条对角线平分一组对角.
知识梳理
3.菱形的判定:
有一组邻边相等的平行四边形叫做菱形
四条边都相等的四边形是菱形
对角线互相垂直的平行四边形是菱形.
方法1:
方法2:
方法3:
4.菱形面积的计算:
菱形的面积 = 底×高 = 对角线乘积的一半
知识梳理
1.如图,四边形ABCD是菱形,AC=8,DB=6,DH⊥AB于点H,则DH等于____.
2.如图,在菱形ABCD中,下列结论错误的是( )
A.BO=DO B.∠DAC=∠BAC
C.AC⊥BD D.AO=DO
D
对点训练
3.如图,四边形ABCD是菱形,CE⊥AB交AB的延长线于点E,CF⊥AD交AD的延长线于点F.求证:CE=CF.
证明:连接AC.
∵四边形ABCD是菱形,
∴AC平分∠DAB.
∵CE⊥AB,CF⊥AD,
∴CE=CF.
A
D
F
C
B
E
菱形是轴对称图形,它的两条对角线所在的直线都是它的对称轴,每条对角线平分一组对角.
对点训练
4.如图,△ABC与△CDE都是等边三角形,点E,F分别在AC,BC上,且EF∥AB.求证:四边形EFCD是菱形.
证明:∵△ABC与△CDE都是等边三角形,
∴ED=CD,∠A=∠DCE=∠BCA=∠DEC=60°,
∴AB∥CD,DE∥CF.
又∵EF∥AB,
∴EF∥CD,
∴四边形EFCD是平行四边形.
∵ED=CD,
∴四边形EFCD是菱形.
对点训练
正方形的性质及判定
1.定义:有一组邻边相等并且有一个角是直角的平行四边形叫正方形.
2.正方形的性质
正方形的四个角都是直角;
正方形的四条边都相等;
正方形的对角线相等,并且互相垂直平分;
正方形是轴对称图形,它有四条对称轴.
知识梳理
正方形
矩形
有一组邻边相等
菱形
有一个角是直角
有一组邻边相等
且有一个角是直角
3.正方形常见的判定方法
先证是矩形再证是菱形或先证是菱形再证是矩形
平行四边形
知识梳理
5种判定方法
三个角是直角
四条边相等
一个角是直角
或对角线相等
一组邻边相等
或对角线互相垂直
一组邻边相等
或对角线互相垂直
一个角是直角
或对角线相等
一个角是直角且一组邻边相等
平行四边形、矩形、菱形、正方形的判定小结
知识梳理
1.如图,在菱形ABCD中,∠B=60°,AB=4,则以AC为边长的正方形ACEF的周长为( )
A.14 B . 15
C.16 D.17
C
2.如图,在正方形ABCD的外侧作等边三角形ADE,则∠BED的度数是______.
45°
对点训练
3.如图,在△ABC中,AB=AC,AD是△ABC的角平分线,点O为边AB的中点,连接DO并延长到点E,使OE=OD,连接AE,BE.
(1)求证:四边形AEBD是矩形;
解:(1)∵点O为AB的中点,
∴BO=AO.
又∵OE=OD,
∴四边形AEBD是平行四边形.
∵AB=AC,AD是△ABC的角平分线,
∴AD⊥BC,
∴∠ADB=90°,
∴四边形AEBD是矩形;
对点训练
(2)当∠BAC=90°时,矩形AEBD是正方形.
理由如下:∵∠BAC=90°,AB=AC,
AD是△ABC的角平分线,
由(1),得四边形AEBD是矩形,
∴矩形AEBD是正方形.(答案不唯一,言之有理即可)
对点训练
3.如图,在△ABC中,AB=AC,AD是△ABC的角平分线,点O为边AB的中点,连接DO并延长到点E,使OE=OD,连接AE,BE.
(2)当△ABC满足什么条件时,矩形AEBD是正方形.并说明理由.
(0,2),(0,-2),(2,0)
提升训练
D
提升训练
提升训练
提升训练
提升训练
提升训练
提升训练
提升训练
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
第五章 特殊平行四边形
章末复习
浙教版 八年级下册
知识梳理
矩形的性质及判定
1.定义:有一个角是直角的平行四边形叫做矩形.也叫做长方形.
矩形是特殊的平行四边形.
矩形除了具有平行四边形所有性质,还具有的性质有:
矩形的对角线相等
2.矩形的性质:
矩形的四个角都是直角
边
角
对角线
对称性
平行四边形
矩形
对边平行
且相等
对角相等
邻角互补
对角线互
相平分
中心对称图形
对边平行
且相等
四个角
为直角
对角线互相
平分且相等
中心对称图形
轴对称图形
知识梳理
有一个角是直角的平行四边形是矩形.
对角线相等的平行四边形是矩形 .
(对角线相等且互相平分的四边形是矩形.)
有三个角是直角的四边形是矩形 .
方法1:
方法2:
方法3:
3.矩形的判定:
知识梳理
1.在矩形ABCD中,O是BC的中点,∠AOD=90°,矩形ABCD的周长为24 cm,则AB的长为( )
A.1 cm B.2 cm C.2.5 cm D.4 cm
D
2.四边形ABCD的对角线AC,BD相交于点O,已知下列6个条件:①AB∥DC;②AB=DC;③AC=BD;④∠ABC=90°;⑤OA=OC;⑥OB=OD.能判定四边形ABCD是矩形的有_____________________________________.(填序号)
①②③(或①②④或③⑤⑥或④⑤⑥)
对点训练
3.如图,在矩形ABCD中,E,F分别是边BC,AB上的点,且EF=ED,EF⊥ED.求证:AE平分∠BAD.
证明:∵四边形ABCD是矩形,
∴∠B=∠C=∠BAD=90°,
AB=CD,AD∥BC,
∴∠BEF+∠BFE=90°.
∵EF⊥ED,
∴∠FED=90°.
∴∠BEF+∠CED=90°,
∴∠BFE=∠CED.
对点训练
∴△EBF≌△DCE(AAS),
在△EBF和△DCE中,
∴BE=CD,
∵AD∥BC,
∴∠BEA=∠EAD,
∴AE平分∠BAD.
∴BE=AB,
∴∠BAE=∠BEA.
∴∠BAE=∠EAD,
对点训练
4.如图,矩形ABCD的对角线相交于点O,E,F,G,H分别是OA,OB,OC,OD上的点,且AE=BF=CG=DH.
求证:四边形EFGH是矩形.
证明:∵四边形ABCD是矩形,
∴OA=OB=OC=OD.
∵AE=BF=CG=DH,
∴AO-AE=OB-BF=CO-CG=DO-DH,
即OE=OF=OG=OH,
∴四边形EFGH是矩形.
对点训练
菱形的性质及判定
1.定义:有一组邻边相等的平行四边形叫做菱形.
菱形是特殊的平行四边形.
菱形除了具有平行四边形所有性质,还具有的性质有:
2.菱形的性质:
菱形的四条边都相等
菱形的两条对角线互相垂直,并且每一条对角线平分一组对角.
知识梳理
3.菱形的判定:
有一组邻边相等的平行四边形叫做菱形
四条边都相等的四边形是菱形
对角线互相垂直的平行四边形是菱形.
方法1:
方法2:
方法3:
4.菱形面积的计算:
菱形的面积 = 底×高 = 对角线乘积的一半
知识梳理
1.如图,四边形ABCD是菱形,AC=8,DB=6,DH⊥AB于点H,则DH等于____.
2.如图,在菱形ABCD中,下列结论错误的是( )
A.BO=DO B.∠DAC=∠BAC
C.AC⊥BD D.AO=DO
D
对点训练
3.如图,四边形ABCD是菱形,CE⊥AB交AB的延长线于点E,CF⊥AD交AD的延长线于点F.求证:CE=CF.
证明:连接AC.
∵四边形ABCD是菱形,
∴AC平分∠DAB.
∵CE⊥AB,CF⊥AD,
∴CE=CF.
A
D
F
C
B
E
菱形是轴对称图形,它的两条对角线所在的直线都是它的对称轴,每条对角线平分一组对角.
对点训练
4.如图,△ABC与△CDE都是等边三角形,点E,F分别在AC,BC上,且EF∥AB.求证:四边形EFCD是菱形.
证明:∵△ABC与△CDE都是等边三角形,
∴ED=CD,∠A=∠DCE=∠BCA=∠DEC=60°,
∴AB∥CD,DE∥CF.
又∵EF∥AB,
∴EF∥CD,
∴四边形EFCD是平行四边形.
∵ED=CD,
∴四边形EFCD是菱形.
对点训练
正方形的性质及判定
1.定义:有一组邻边相等并且有一个角是直角的平行四边形叫正方形.
2.正方形的性质
正方形的四个角都是直角;
正方形的四条边都相等;
正方形的对角线相等,并且互相垂直平分;
正方形是轴对称图形,它有四条对称轴.
知识梳理
正方形
矩形
有一组邻边相等
菱形
有一个角是直角
有一组邻边相等
且有一个角是直角
3.正方形常见的判定方法
先证是矩形再证是菱形或先证是菱形再证是矩形
平行四边形
知识梳理
5种判定方法
三个角是直角
四条边相等
一个角是直角
或对角线相等
一组邻边相等
或对角线互相垂直
一组邻边相等
或对角线互相垂直
一个角是直角
或对角线相等
一个角是直角且一组邻边相等
平行四边形、矩形、菱形、正方形的判定小结
知识梳理
1.如图,在菱形ABCD中,∠B=60°,AB=4,则以AC为边长的正方形ACEF的周长为( )
A.14 B . 15
C.16 D.17
C
2.如图,在正方形ABCD的外侧作等边三角形ADE,则∠BED的度数是______.
45°
对点训练
3.如图,在△ABC中,AB=AC,AD是△ABC的角平分线,点O为边AB的中点,连接DO并延长到点E,使OE=OD,连接AE,BE.
(1)求证:四边形AEBD是矩形;
解:(1)∵点O为AB的中点,
∴BO=AO.
又∵OE=OD,
∴四边形AEBD是平行四边形.
∵AB=AC,AD是△ABC的角平分线,
∴AD⊥BC,
∴∠ADB=90°,
∴四边形AEBD是矩形;
对点训练
(2)当∠BAC=90°时,矩形AEBD是正方形.
理由如下:∵∠BAC=90°,AB=AC,
AD是△ABC的角平分线,
由(1),得四边形AEBD是矩形,
∴矩形AEBD是正方形.(答案不唯一,言之有理即可)
对点训练
3.如图,在△ABC中,AB=AC,AD是△ABC的角平分线,点O为边AB的中点,连接DO并延长到点E,使OE=OD,连接AE,BE.
(2)当△ABC满足什么条件时,矩形AEBD是正方形.并说明理由.
(0,2),(0,-2),(2,0)
提升训练
D
提升训练
提升训练
提升训练
提升训练
提升训练
提升训练
提升训练
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
同课章节目录
- 第一章 二次根式
- 1.1 二次根式
- 1.2 二次根式的性质
- 1.3 二次根式的运算
- 第二章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程的应用
- 2.4 一元二次方程根与系数的关系(选学)
- 第三章 数据分析初步
- 3.1 平均数
- 3.2 中位数和众数
- 3.3 方差和标准差
- 第四章 平行四边形
- 4.1 多边形
- 4.2 平行四边形
- 4.3 中心对称
- 4.4 平行四边形的判定
- 4.5 三角形的中位线
- 4.6 反证法
- 第五章 特殊平行四边形
- 5.1 矩形
- 5.2 菱形
- 5.3 正方形
- 第六章 反比例函数
- 6.1 反比例函数
- 6.2 反比例函数的图象和性质
- 6.3 反比例函数的应用
