浙教版数学九下 第1章 解直角三角形复习课 课件(共18张PPT)
文档属性
| 名称 | 浙教版数学九下 第1章 解直角三角形复习课 课件(共18张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 956.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-06 00:00:00 | ||
图片预览




文档简介
(共18张PPT)
2021.12
一、基本概念
1.正弦
A
B
C
a
c
sinA=
2.余弦
b
cosA=
3.正切
tanA=
锐角A的正弦、余弦、正切、都叫做∠A的锐角三角函数.
定义:
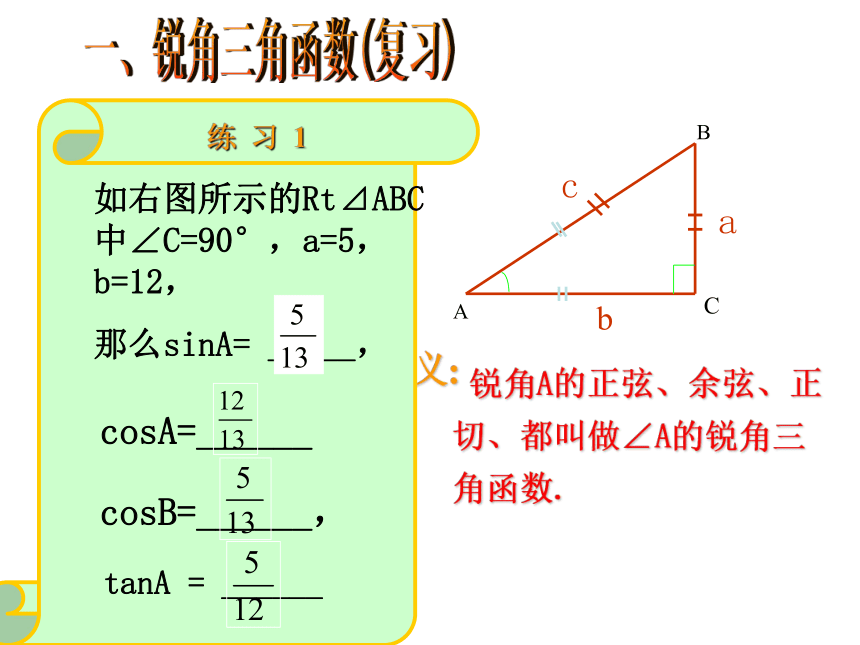
练 习 1
如右图所示的Rt⊿ABC中∠C=90°,a=5,b=12,
那么sinA= _____,
tanA = ______
cosB=______,
cosA=______
2
tanα
cosα
sinα
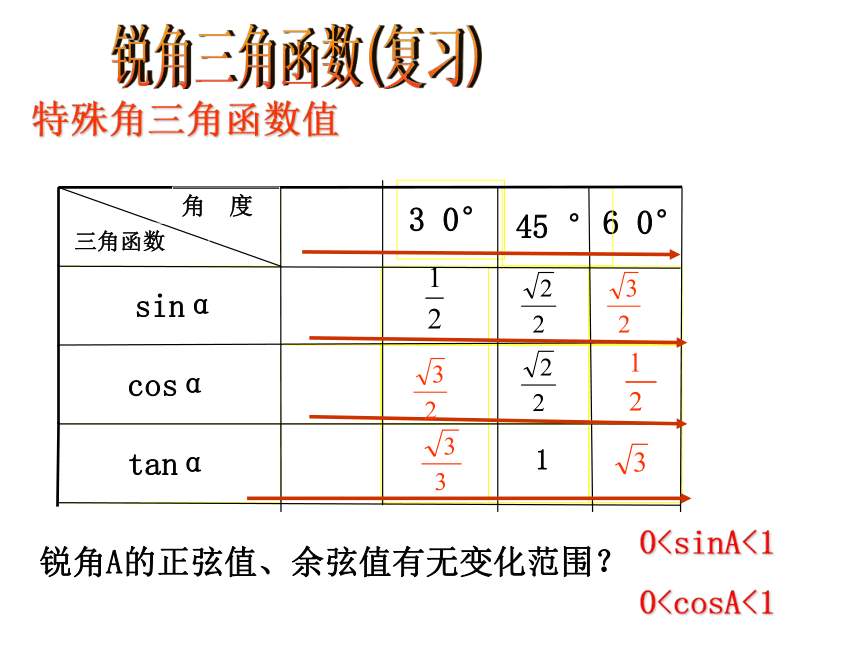
6 0°
45 °
3 0°
角 度
三角函数
特殊角三角函数值
1
锐角A的正弦值、余弦值有无变化范围?
00例1
(1)计算:sin60°·tan60°+cos 45°=
(2)如果tanA·tan30°=1,∠A=_________。
(3)已知cosα<0.5,那么锐角α的取值范围是( )
A、60°<α<90° B、0°< α <60° C、30°< α <90° D、0°< α <30°
A、直角三角形 B、锐角三角形 C、钝角三角形 D、等边三角形
2
60°
A
D
那么△ABC是( )
(4)如果
1、若tan(β+20°)= ,β为锐角,则β=____
2、已知A是锐角,且tanA=3,则
3、在Rt△ABC中,∠C=90°cosB= ,则sinB的值为__ ;
40°
练一练
4、已知锐角A的顶点在原点,始边为x轴的正半轴,终边经过点(3,4),则sinA= ,cosA= ;tanA= ;
8、已知在Rt△ABC中, ∠C=90°,sinA= ,则 cosB=( )
5、在Rt△ABC中,如果各边都扩大2倍,则锐角A的正弦值和余弦值( )
A、都不变 B、都扩大2倍 C、都缩小2倍 D、不确定
6、在△ABC中,若
sinA= , tanB=√3,则∠C=
√2
2
7、如果α和β都是锐角,且sinα= cosβ,则α与β的关系是( )
A、相等 B、互余 C、互补 D、不确定
A
75°
B
A
练一练
A、 B、 C、 D、
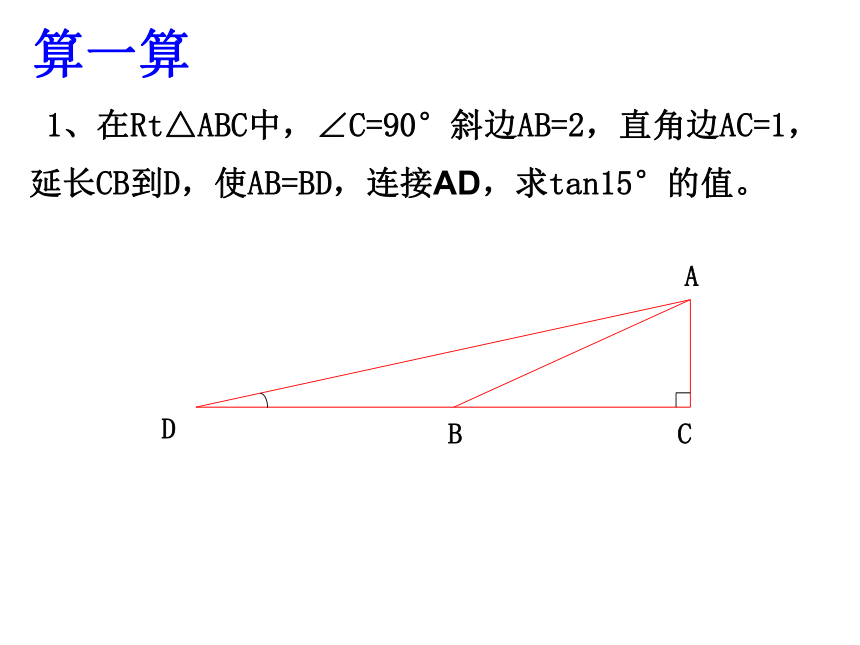
1、在Rt△ABC中,∠C=90°斜边AB=2,直角边AC=1,延长CB到D,使AB=BD,连接AD,求tan15°的值。
D
A
C
B
算一算
A
B
D
C
算一算
2、如图,在⊿ABC中, ∠C=90°, ∠ABC=60°,AB=2,
D是AC的中点,那么sin∠DBC的值=___________
1、三边之间的关系:
a2+b2=c2(勾股定理);
2、锐角之间的关系:
∠A+∠B=90
3、边角之间的关系:
tanA=
a
b
sinA=
a
c
二、解直角三角形
cosA=
b
c
A
C
B
a
b
c
知一边一锐角解直角三角形
知两边解直角三角形
非直角三角形:添设辅助线转化为
解直角三角形
解直角三角形
直角三角形
的边角关系
三角形解直角
l
h
α
1、坡度
i=
h
l
= tanα
(α为坡角)
解直角三角形
铅直线
水平线
视线
视线
仰角
俯角
2、仰角和俯角
解直角三角形的两种基本图形:
A
A
B
B
C
C
D
D
解直角三角形
1、在下列直角三角形中,不能解的是( )
A、知一直角边和所对的角 B、已知两个锐角
C、已知斜边和一个锐角 D、已知两直角边
2、在△ABC中,∠C=90°,根据下列条件解这个直角三角形。
(3)∠A=300,斜边上的高CD= ,则AB= ;
B
(1)若∠A=300,b=10,则a= ,c= ;
(2)若sinA= ,c=x+2,a=x,则b= ,cosA= ;
试一试
例2、如图学校里有一块三角形形状的花圃ABC,现测得∠A=30°, AC=40m,BC=25m,请你帮助计算一下这块花圃的面积
A
C
B
D
例3、如图,在△ABC中,AD是BC边上的高,
若tanB=cos∠DAC,
(1)AC与BD相等吗?说明理由;
(2)若sinC= ,BC=12,求AD的长。
12
13
D
C
B
A
例4、如图,海岛A四周20海里周围内为暗礁区,一艘货轮由东向西航行,在B处见岛A在北偏西60 方向,航行24海里到C处,见岛A在北偏西30 方向,货轮继续向西航行,有无触礁的危险?
A
B
D
C
N
N1
30
60
4、如图,为了测量山坡的护坡石坝与地面的倾斜角α,把一根长为4.5m的竹竿AC斜靠在石坝旁,量出竹竿长1m处,它离地面的高度为0.6m,又量得竿顶与坝脚的距离BC=2.8m.这样∠α求就可以算出来了.请你算一算.
练一练
小结
这节课你有什么收获?
作业:1、课文P29-31
2、作业本(1)复习题A组必做
2021.12
一、基本概念
1.正弦
A
B
C
a
c
sinA=
2.余弦
b
cosA=
3.正切
tanA=
锐角A的正弦、余弦、正切、都叫做∠A的锐角三角函数.
定义:
练 习 1
如右图所示的Rt⊿ABC中∠C=90°,a=5,b=12,
那么sinA= _____,
tanA = ______
cosB=______,
cosA=______
2
tanα
cosα
sinα
6 0°
45 °
3 0°
角 度
三角函数
特殊角三角函数值
1
锐角A的正弦值、余弦值有无变化范围?
0
(1)计算:sin60°·tan60°+cos 45°=
(2)如果tanA·tan30°=1,∠A=_________。
(3)已知cosα<0.5,那么锐角α的取值范围是( )
A、60°<α<90° B、0°< α <60° C、30°< α <90° D、0°< α <30°
A、直角三角形 B、锐角三角形 C、钝角三角形 D、等边三角形
2
60°
A
D
那么△ABC是( )
(4)如果
1、若tan(β+20°)= ,β为锐角,则β=____
2、已知A是锐角,且tanA=3,则
3、在Rt△ABC中,∠C=90°cosB= ,则sinB的值为__ ;
40°
练一练
4、已知锐角A的顶点在原点,始边为x轴的正半轴,终边经过点(3,4),则sinA= ,cosA= ;tanA= ;
8、已知在Rt△ABC中, ∠C=90°,sinA= ,则 cosB=( )
5、在Rt△ABC中,如果各边都扩大2倍,则锐角A的正弦值和余弦值( )
A、都不变 B、都扩大2倍 C、都缩小2倍 D、不确定
6、在△ABC中,若
sinA= , tanB=√3,则∠C=
√2
2
7、如果α和β都是锐角,且sinα= cosβ,则α与β的关系是( )
A、相等 B、互余 C、互补 D、不确定
A
75°
B
A
练一练
A、 B、 C、 D、
1、在Rt△ABC中,∠C=90°斜边AB=2,直角边AC=1,延长CB到D,使AB=BD,连接AD,求tan15°的值。
D
A
C
B
算一算
A
B
D
C
算一算
2、如图,在⊿ABC中, ∠C=90°, ∠ABC=60°,AB=2,
D是AC的中点,那么sin∠DBC的值=___________
1、三边之间的关系:
a2+b2=c2(勾股定理);
2、锐角之间的关系:
∠A+∠B=90
3、边角之间的关系:
tanA=
a
b
sinA=
a
c
二、解直角三角形
cosA=
b
c
A
C
B
a
b
c
知一边一锐角解直角三角形
知两边解直角三角形
非直角三角形:添设辅助线转化为
解直角三角形
解直角三角形
直角三角形
的边角关系
三角形解直角
l
h
α
1、坡度
i=
h
l
= tanα
(α为坡角)
解直角三角形
铅直线
水平线
视线
视线
仰角
俯角
2、仰角和俯角
解直角三角形的两种基本图形:
A
A
B
B
C
C
D
D
解直角三角形
1、在下列直角三角形中,不能解的是( )
A、知一直角边和所对的角 B、已知两个锐角
C、已知斜边和一个锐角 D、已知两直角边
2、在△ABC中,∠C=90°,根据下列条件解这个直角三角形。
(3)∠A=300,斜边上的高CD= ,则AB= ;
B
(1)若∠A=300,b=10,则a= ,c= ;
(2)若sinA= ,c=x+2,a=x,则b= ,cosA= ;
试一试
例2、如图学校里有一块三角形形状的花圃ABC,现测得∠A=30°, AC=40m,BC=25m,请你帮助计算一下这块花圃的面积
A
C
B
D
例3、如图,在△ABC中,AD是BC边上的高,
若tanB=cos∠DAC,
(1)AC与BD相等吗?说明理由;
(2)若sinC= ,BC=12,求AD的长。
12
13
D
C
B
A
例4、如图,海岛A四周20海里周围内为暗礁区,一艘货轮由东向西航行,在B处见岛A在北偏西60 方向,航行24海里到C处,见岛A在北偏西30 方向,货轮继续向西航行,有无触礁的危险?
A
B
D
C
N
N1
30
60
4、如图,为了测量山坡的护坡石坝与地面的倾斜角α,把一根长为4.5m的竹竿AC斜靠在石坝旁,量出竹竿长1m处,它离地面的高度为0.6m,又量得竿顶与坝脚的距离BC=2.8m.这样∠α求就可以算出来了.请你算一算.
练一练
小结
这节课你有什么收获?
作业:1、课文P29-31
2、作业本(1)复习题A组必做
