5.6三角形的中位线 学案

预习是展示之本 展示是学习之魂 班级 姓名 学号
5.6三角形的中位线(学案)
一、智慧航标
1.了解三角形的中位线的概念.
2.了解三角形的中位线的性质.
3.探索三角形的中位线的性质的一些简单的应用.
教学重点与难点
教学重点：三角形的中位线定理.
教学难点：三角形的中位线定理的证明中添加辅助线的思想方法.
预习指导：阅读教材P117-118页内容，了解三角形的中位线的概念.了解三角形的中位线的性质.探索三角形的中位线的性质的一些简单的应用.仿照例题格式完成学案。记下你疑难之处和学习经验，课上交流。
二、智慧起航
（一）智慧激趣
1. 如图，中，已知AB=8，BC=6，CA=4，DE是中位线，则DE=（ ）
A. 4 B. 3 C. 2 D. 1
2. 任何一个三角形有 条中位线.
3. 如图是一个三角形与它的三条中位线，则图中有 个平行四边形.
4.如图，在中，D，E分别是AB，AC的中点，若DE=5，则BC的长是 .
（二）探索新知
1.动手操作：剪一刀，将一张三角形纸片剪成一张三角形纸片和一张梯形纸片
（1）如果要求剪得的两张纸片能拼成平行的四边形，剪痕的位置有什么要求？
（2）要把所剪得的两个图形拼成一个平行四边形，可将其中的三角形做怎样的图形变换？
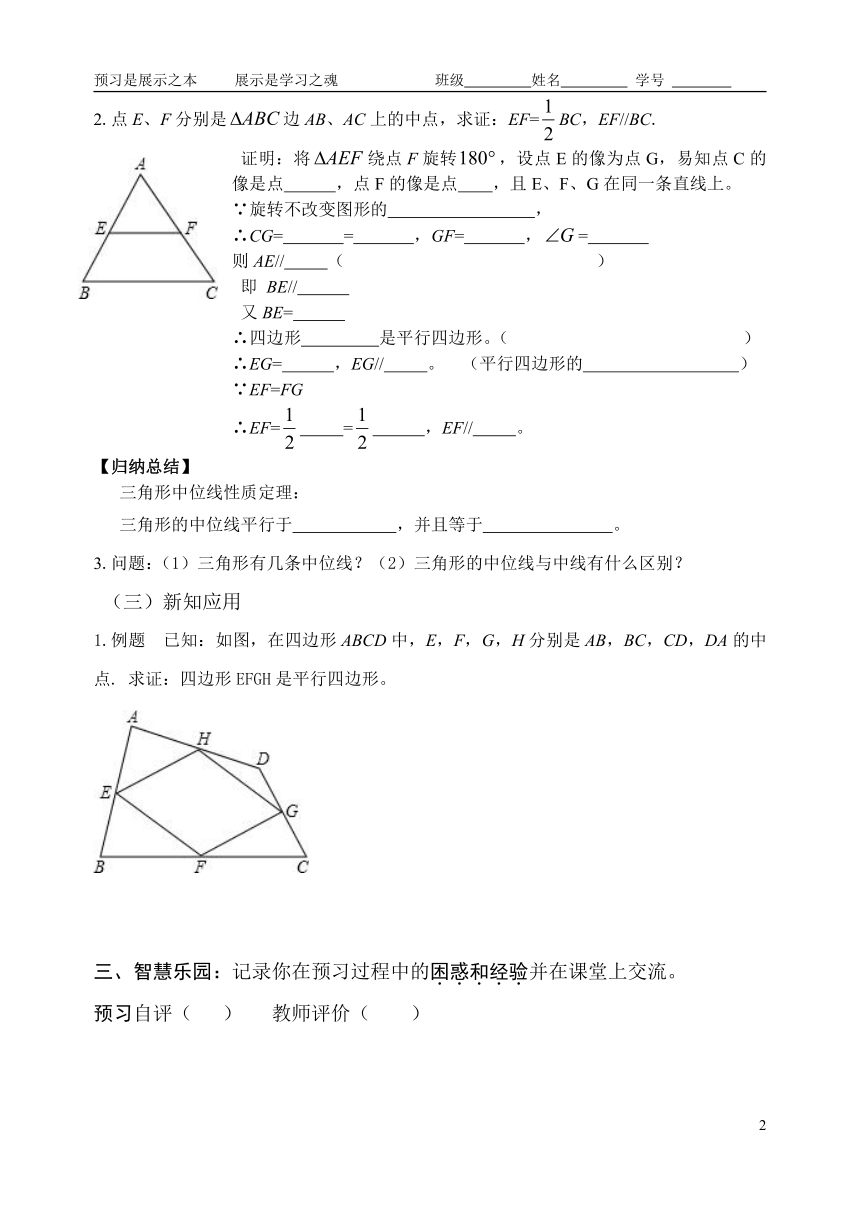
2.点E、F分别是边AB、AC上的中点，求证：EF=BC，EF//BC.
证明：将绕点F旋转，设点E的像为点G，易知点C的像是点 ，点F的像是点 ，且E、F、G在同一条直线上。
∵旋转不改变图形的 ，
∴CG= = ，GF= ，=
则AE// （ ）
即 BE//
又BE=
∴四边形 是平行四边形。（ ）
∴EG= ，EG// 。 （平行四边形的 ）
∵EF=FG
∴EF= = ，EF// 。
【归纳总结】
三角形中位线性质定理：
三角形的中位线平行于 ，并且等于 。
3.问题：（1）三角形有几条中位线？（2）三角形的中位线与中线有什么区别？
（三）新知应用
1.例题 已知：如图，在四边形ABCD中，E，F，G，H分别是AB，BC，CD，DA的中点. 求证：四边形EFGH是平行四边形。
三、智慧乐园：记录你在预习过程中的困惑和经验并在课堂上交流。
预习自评（ ） 教师评价（ ）
四、课堂小结
五、智慧大道
1.三角形的周长为18cm，它的三条中位线围城三角形的周长是 .
2.已知：如图，DE，EF是△ABC的两条中位线.求证：四边形BFED是平行四边形.
3.如图，DE是△ABC的中位线，AF是BC边上的中线，DE和AF交于点O，
求证：DE与AF互相平分.
4.取任意一张三角形纸片，你能把它剪成四个全等的三角形吗？请说明你的方法，并画出示意图.
5.一块白铁皮零料形状如图，要从中裁出一块平行四边形白铁皮，并使四个顶点分别落在原白铁皮的四条边上.可以怎样裁？如果原白铁皮的面积为100cm ，要求裁出的平行四边形的面积等于50cm ，能办到吗？请说明理由.
6.已知：如图，△ABC是锐角三角形，分别以AB，AC为边向外侧作等边三角形ABM和等边三角形CAN.D，E，F分别是MB，BC，CN的中点，连结DE，FE.求证：DE=FE.
第1题
第3题
第4题
第2题
第5题
第6题
第3题
PAGE
1