浙教版数学七年级上册:5.4.2 等积变形问题 同步新授课件(共16张PPT)
文档属性
| 名称 | 浙教版数学七年级上册:5.4.2 等积变形问题 同步新授课件(共16张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 278.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-08 00:00:00 | ||
图片预览





文档简介
(共16张PPT)
第五章 一元一次方程
5.4 一元一次方程的应用
第2课时 等积变形问题
知识回顾
全班同学去划船,若减少一条船,每条船正好坐9名同学,若增加一条船,每条船正好坐6名同学,则原有多少条船?
解:设原有x条船.根据题意,得
9(x-1)=6(x+1).
去括号,得9x-9=6x+6.
移项,得9x-6x=6+9.
合并同类项,得3x=15.
两边同除以3,得x=5.
答:原有5条船.
获取新知
h
R
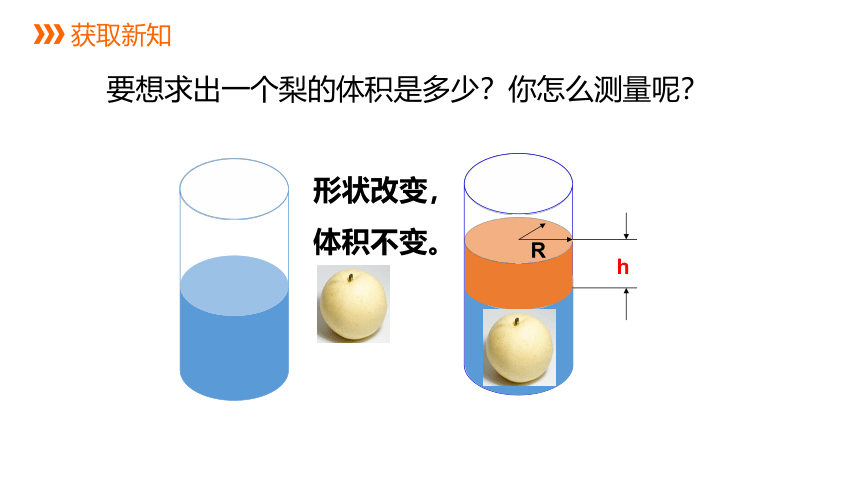
要想求出一个梨的体积是多少?你怎么测量呢?
形状改变,
体积不变。
例题精讲
例3 一纪念碑建筑的底面呈正方形,其四周铺上花岗石,形成一个宽为3.2米的正方形边框(如图中阴影部分),已知铺这个边框恰好用了144块边长为0.8米的正方形花岗石(接缝忽略不计),问纪念碑建筑底面的边长是多少米
3.2
3.2
x
分析 如图所示,用x表示中间空白正方形的边长,本题的数量关系是:
阴影部分的面积=144块边长为0.8米的正方形花岗岩石的面积;
——————————————————————————阴影部分可以分割成4个长为(x+3.2)米,宽为3.2米的长方形
解:设标志性建筑底面的边长为x米,根据题意,得
4×3.2(x+3.2)=0.8×0.8×144
解这个方程,得x=4.
答:这一标志性建筑的底面边长为4米.
1.在应用方程解决有关实际问题时,清楚地分辨量之间的关系,尤其相等关系是建立方程的关键.
2.解题中的检验对确保答案的正确和合理很有帮助,但具体过程可省略不写.
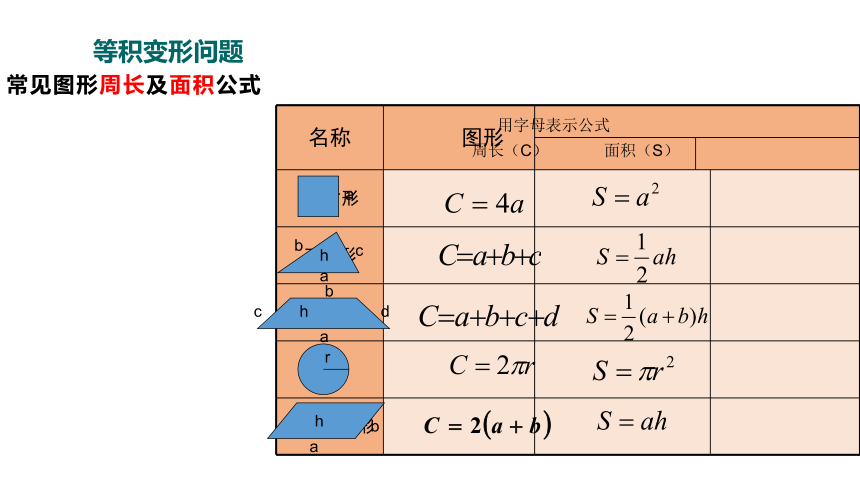
常见图形周长及面积公式
名称 图形 正方形
三角形
梯形
圆
平行四边形
r
a
b
h
c
d
a
h
b
c
a
a
h
b
用字母表示公式
周长(C)
面积(S)
等积变形问题
例4 如图所示,用直径200mm的钢柱锻造一块长、 宽、高分别为300mm,300mm和80mm的长方体毛胚底板,问应截取钢柱多少长(不计损耗,结果误差不超过1mm)
分析 钢柱在锻造过程中体积不变,即
截取的圆柱体体积=锻造成的长方体体积
解 设截取圆柱的高为x(mm),根据题意,得
π×1002×x=300×300×80
解这个方程,得x= ≈230
720
——
π
答:应截取钢柱的长约230mm
随堂演练
1.一根细绳可围成边长为7 cm的正方形,若将此细绳改围成长比宽大2 cm的长方形,则该长方形的长、宽分别是多少厘米?
解:设长方形的长为x cm,则宽为(x-2)cm.
根据题意,得2x+2(x-2)=4×7,
解得x=8.
∴x-2=6.
答:该长方形的长是8 cm,宽是6 cm.
2.如图所示,小明将一张正方形纸片剪去一个宽为4厘米的长条后,再从剩下的长方形纸片上剪去一个宽为5厘米的长条.如果两次剪下的长条面积正好相等,那么每一个长条的面积为多少?
解:设该正方形的边长为x厘米.
由题意,得4x=5(x-4),
解得x=20.
4x=80.
答:每一个长条的面积是80平方厘米.
3.某车间要锻造直径为40毫米,高为45毫米的圆柱形零件毛坯,需截取直径为30毫米的圆钢多长?
根据题意,得π× ×45=π× ·x.
整理,得400×45=152·x.
解得x=80.
答:需截取直径为30毫米的圆钢80毫米.
解:设需截取直径为30毫米的圆钢x毫米.
40 2
( — )
2
30 2
( — )
2
4.一个底面直径为16厘米的圆柱形木桶内装满水,水中淹没着一个底面直径为8厘米、高为15厘米的铁质小圆柱体.当铁质小圆柱体取出后,木桶内水面下降了多少?
[解析] 木桶内水面下降的圆柱体体积=铁质小圆柱体体积.
解:设木桶内水面下降xcm.由题意得:
解方程得:
答:木桶内水面下降
课堂小结
一元一次方程的应用
列方程解应用题
步骤
审题,找等量关系
设未知数
列、解一元一次方程
检验并写出答案
关键
找相等关系
体积、面积不变
等积变
形问题
常见体积公式
常见面积公式
第五章 一元一次方程
5.4 一元一次方程的应用
第2课时 等积变形问题
知识回顾
全班同学去划船,若减少一条船,每条船正好坐9名同学,若增加一条船,每条船正好坐6名同学,则原有多少条船?
解:设原有x条船.根据题意,得
9(x-1)=6(x+1).
去括号,得9x-9=6x+6.
移项,得9x-6x=6+9.
合并同类项,得3x=15.
两边同除以3,得x=5.
答:原有5条船.
获取新知
h
R
要想求出一个梨的体积是多少?你怎么测量呢?
形状改变,
体积不变。
例题精讲
例3 一纪念碑建筑的底面呈正方形,其四周铺上花岗石,形成一个宽为3.2米的正方形边框(如图中阴影部分),已知铺这个边框恰好用了144块边长为0.8米的正方形花岗石(接缝忽略不计),问纪念碑建筑底面的边长是多少米
3.2
3.2
x
分析 如图所示,用x表示中间空白正方形的边长,本题的数量关系是:
阴影部分的面积=144块边长为0.8米的正方形花岗岩石的面积;
——————————————————————————阴影部分可以分割成4个长为(x+3.2)米,宽为3.2米的长方形
解:设标志性建筑底面的边长为x米,根据题意,得
4×3.2(x+3.2)=0.8×0.8×144
解这个方程,得x=4.
答:这一标志性建筑的底面边长为4米.
1.在应用方程解决有关实际问题时,清楚地分辨量之间的关系,尤其相等关系是建立方程的关键.
2.解题中的检验对确保答案的正确和合理很有帮助,但具体过程可省略不写.
常见图形周长及面积公式
名称 图形 正方形
三角形
梯形
圆
平行四边形
r
a
b
h
c
d
a
h
b
c
a
a
h
b
用字母表示公式
周长(C)
面积(S)
等积变形问题
例4 如图所示,用直径200mm的钢柱锻造一块长、 宽、高分别为300mm,300mm和80mm的长方体毛胚底板,问应截取钢柱多少长(不计损耗,结果误差不超过1mm)
分析 钢柱在锻造过程中体积不变,即
截取的圆柱体体积=锻造成的长方体体积
解 设截取圆柱的高为x(mm),根据题意,得
π×1002×x=300×300×80
解这个方程,得x= ≈230
720
——
π
答:应截取钢柱的长约230mm
随堂演练
1.一根细绳可围成边长为7 cm的正方形,若将此细绳改围成长比宽大2 cm的长方形,则该长方形的长、宽分别是多少厘米?
解:设长方形的长为x cm,则宽为(x-2)cm.
根据题意,得2x+2(x-2)=4×7,
解得x=8.
∴x-2=6.
答:该长方形的长是8 cm,宽是6 cm.
2.如图所示,小明将一张正方形纸片剪去一个宽为4厘米的长条后,再从剩下的长方形纸片上剪去一个宽为5厘米的长条.如果两次剪下的长条面积正好相等,那么每一个长条的面积为多少?
解:设该正方形的边长为x厘米.
由题意,得4x=5(x-4),
解得x=20.
4x=80.
答:每一个长条的面积是80平方厘米.
3.某车间要锻造直径为40毫米,高为45毫米的圆柱形零件毛坯,需截取直径为30毫米的圆钢多长?
根据题意,得π× ×45=π× ·x.
整理,得400×45=152·x.
解得x=80.
答:需截取直径为30毫米的圆钢80毫米.
解:设需截取直径为30毫米的圆钢x毫米.
40 2
( — )
2
30 2
( — )
2
4.一个底面直径为16厘米的圆柱形木桶内装满水,水中淹没着一个底面直径为8厘米、高为15厘米的铁质小圆柱体.当铁质小圆柱体取出后,木桶内水面下降了多少?
[解析] 木桶内水面下降的圆柱体体积=铁质小圆柱体体积.
解:设木桶内水面下降xcm.由题意得:
解方程得:
答:木桶内水面下降
课堂小结
一元一次方程的应用
列方程解应用题
步骤
审题,找等量关系
设未知数
列、解一元一次方程
检验并写出答案
关键
找相等关系
体积、面积不变
等积变
形问题
常见体积公式
常见面积公式
同课章节目录
- 第1章 有理数
- 1.1 从自然数到有理数
- 1.2 数轴
- 1.3 绝对值
- 1.4 有理数大小比较
- 第2章 有理数的运算
- 2.1 有理数的加法
- 2.2 有理数的减法
- 2.3 有理数的乘法
- 2.4 有理数的除法
- 2.5 有理数的乘方
- 2.6 有理数的混合运算
- 2.7 近似数
- 第3章 实数
- 3.1 平方根
- 3.2 实数
- 3.3 立方根
- 3.4 实数的运算
- 第4章 代数式
- 4.1 用字母表示数
- 4.2 代数式
- 4.3 代数式的值
- 4.4 整式
- 4.5 合并同类项
- 4.6 整式的加减
- 第5章 一元一次方程
- 5.1 一元一次方程
- 5.2 等式的基本性质
- 5.3 一元一次方程的解法
- 5.4 一元一次方程的应用
- 第6章 图形的初步知识
- 6.1 几何图形
- 6.2 线段、射线和直线
- 6.3 线段的长短比较
- 6.4 线段的和差
- 6.5 角与角的度量
- 6.6 角的大小比较
- 6.7 角的和差
- 6.8 余角和补角
- 6.9 直线的相交
