浙教版数学七年级上册:5.4.3 调配与工程问题 同步新授课件(共17张PPT)
文档属性
| 名称 | 浙教版数学七年级上册:5.4.3 调配与工程问题 同步新授课件(共17张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 134.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-08 00:00:00 | ||
图片预览





文档简介
(共17张PPT)
第五章 一元一次方程
5.4 一元一次方程的应用
第3课时 调配与工程问题
知识回顾
把一个长、宽、高分别为8 cm,7 cm,6 cm的长方体铁块和一个棱长为5 cm的正方体铁块熔炼成一个底面直径为20 cm的圆柱体,则这个圆柱体的高是多少?(结果精确到0.01 cm)
根据题意,得8×7×6+53=π× ·x,
解得x≈1.47.
解:设这个圆柱体的高是x cm.
20 2
( — )
2
答:这个圆柱体的高约为1.47 cm.
例题精讲
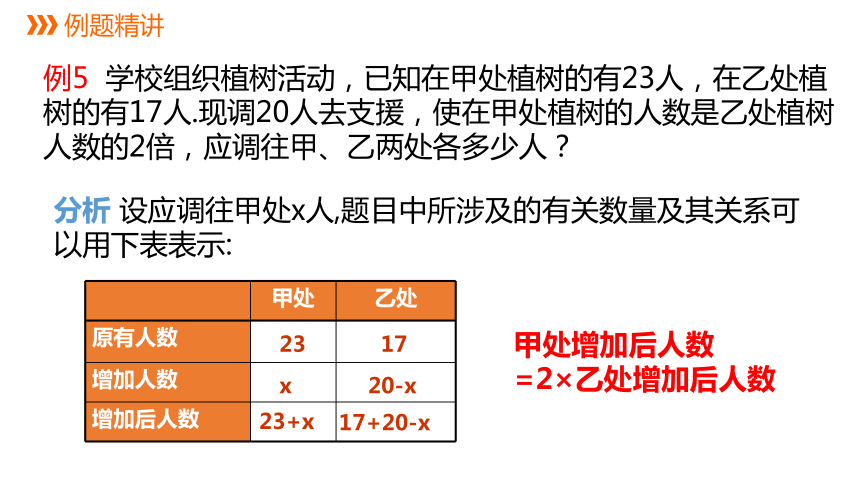
例5 学校组织植树活动,已知在甲处植树的有23人,在乙处植树的有17人.现调20人去支援,使在甲处植树的人数是乙处植树人数的2倍,应调往甲、乙两处各多少人?
分析 设应调往甲处x人,题目中所涉及的有关数量及其关系可以用下表表示:
甲处 乙处
原有人数
增加人数
增加后人数
23+x
20-x
x
23
17
17+20-x
甲处增加后人数
=2×乙处增加后人数
解 设应调往甲处x人,根据题意,得
23+x=2(17+20-x)
解这个方程,得 x=17
∴ 20-x=20-17=3
答:应调往甲处17人,乙处3人。
例6 甲每天生产某种零件80个,甲生产3天后,乙也加入生产同一种零件,再经过5天,两人共生产这种零件940个,问乙每天生产这种零件多少个?
分析 可以用示意图来分析本题中的数量问题
头3天甲生产
零件的个数
甲后5天生
产的个数
乙后5天生
产的个数
940个
头3天甲
生产零件
的个数
+
后5天甲
生产零件
的个数
后5天乙
生产零件
的个数
+
=940
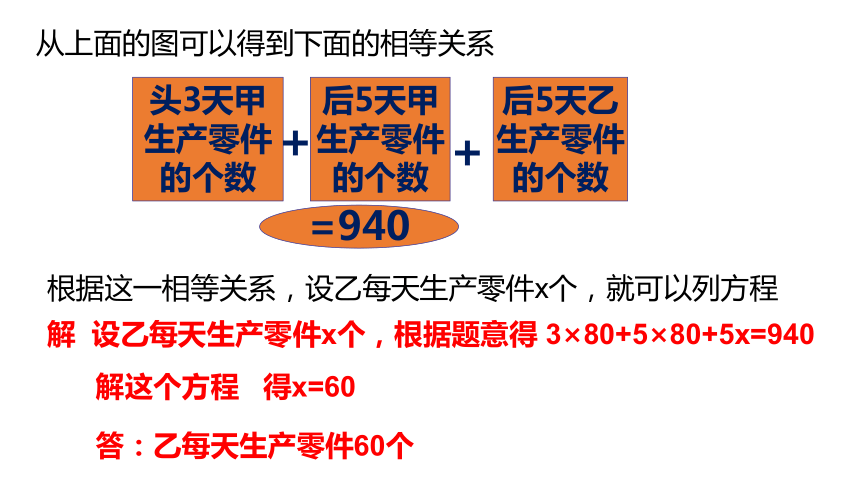
从上面的图可以得到下面的相等关系
根据这一相等关系,设乙每天生产零件x个,就可以列方程
解 设乙每天生产零件x个,根据题意得 3×80+5×80+5x=940
解这个方程 得x=60
答:乙每天生产零件60个
教材补充例题 某车间有22名工人,每人每天可以生产1 200个螺钉或2 000个螺母,1个螺钉需要配2个螺母,为使每天生产的螺钉和螺母刚好配套,应安排生产螺钉和螺母的工人各多少名?
分析:
单日每人生产 个螺钉, 个螺母;
设每日生产螺钉人数为x,则每日生产螺母人数为 人;
每日生产螺钉 个,生产螺母 个;
螺钉和螺母之间的关系 ;
根据螺钉和螺母之间的关系可列方程为 .
2000(22-x)=2×1200x
1200
2000
(22-x)
1200x
2000(22-x)
或螺母数量是螺钉的2倍
螺钉数:螺母数= 1:2
解:设应安排 x 名工人生产螺钉,(22-x)名工人生
产螺母.依题意,得
2000(22-x)=2×1200x .
解方程,得 x=10.
所以 22-x=12.
答:应安排10名工人生产螺钉,12名工人生产螺母.
归纳:
1.分析配套问题时需要注意问题中所涉及的量的比例关系,
比如:1个螺钉需要配2个螺母可表示为螺钉数:螺母数= 1:2;
2.注意通过找到的比例关系列方程;
如:根据螺钉数:螺母数= 1:2
3.可以根据比例式的內项积等于外项积将含比的方程转化为我们熟悉的形式 .
工作量、工作效率、工作时间之间的关系:
(1)工作量=工作效率×工作时间,
工作时间=工作量÷工作效率,
工作效率=工作量÷工作时间;
(2)甲、乙合做的总工作量=甲的工作量+乙的工作量;
(3)甲、乙合做的工作时间=总工作量÷(甲的工作效率+乙的工作效率).
【归纳总结】
获取新知
列表法是分析调配问题数量关系的常用的方法.
随堂演练
1.某商场将一种商品以每件60元的价格售出,盈利20%,
那么该商品的进货价为每件( )
A.80元 B.72元
C.50元 D.36元
C
2. 某班学生分两组参加某项活动,甲组有26人,乙组有32人,后来由于活动需要,从甲组抽调了部分学生去乙组,结果乙组的人数比甲组人数的2倍还多1人.从甲组抽调了多少名学生去乙组?
解:设从甲组抽调了x名学生去乙组.
根据题意,得2(26-x)+1=32+x,解得x=7.
答:从甲组抽调了7名学生去乙组.
3.一件工作,甲单独做需要10小时完成,乙单独做需要15小
时完成,那么甲每小时完成总工作量的________,乙每小时完
成总工作量的________.若设甲、乙合作需要x小时完成,则
可列方程为________________,解得x=________.
1
—
10
1
—
15
x
— +
10
x
— = 1
15
6
4. 有一个加工茶杯的车间,平均每个工人每小时可以加工杯身12个,或者加工杯盖15个.1个杯身配1个杯盖,车间共有90人,则安排多少人加工杯身,才能使每小时加工的杯身和杯盖正好配套?
解:设安排x人加工杯身,
则加工杯盖的人数为________,
每小时加工杯身____个,杯盖__________个,
则可列方程为________________,
解得x=_____.
90-x
12x=15(90-x)
15(90-x)
12x
50
课堂总结
一元一次方程的应用
劳动力调配问题中的相等关系
调配前量的关系
调配后量的关系
工程问题
基本公式:工作量=工作效率×工作时间
相等关系:全部工作量=各部分工作量之和
第五章 一元一次方程
5.4 一元一次方程的应用
第3课时 调配与工程问题
知识回顾
把一个长、宽、高分别为8 cm,7 cm,6 cm的长方体铁块和一个棱长为5 cm的正方体铁块熔炼成一个底面直径为20 cm的圆柱体,则这个圆柱体的高是多少?(结果精确到0.01 cm)
根据题意,得8×7×6+53=π× ·x,
解得x≈1.47.
解:设这个圆柱体的高是x cm.
20 2
( — )
2
答:这个圆柱体的高约为1.47 cm.
例题精讲
例5 学校组织植树活动,已知在甲处植树的有23人,在乙处植树的有17人.现调20人去支援,使在甲处植树的人数是乙处植树人数的2倍,应调往甲、乙两处各多少人?
分析 设应调往甲处x人,题目中所涉及的有关数量及其关系可以用下表表示:
甲处 乙处
原有人数
增加人数
增加后人数
23+x
20-x
x
23
17
17+20-x
甲处增加后人数
=2×乙处增加后人数
解 设应调往甲处x人,根据题意,得
23+x=2(17+20-x)
解这个方程,得 x=17
∴ 20-x=20-17=3
答:应调往甲处17人,乙处3人。
例6 甲每天生产某种零件80个,甲生产3天后,乙也加入生产同一种零件,再经过5天,两人共生产这种零件940个,问乙每天生产这种零件多少个?
分析 可以用示意图来分析本题中的数量问题
头3天甲生产
零件的个数
甲后5天生
产的个数
乙后5天生
产的个数
940个
头3天甲
生产零件
的个数
+
后5天甲
生产零件
的个数
后5天乙
生产零件
的个数
+
=940
从上面的图可以得到下面的相等关系
根据这一相等关系,设乙每天生产零件x个,就可以列方程
解 设乙每天生产零件x个,根据题意得 3×80+5×80+5x=940
解这个方程 得x=60
答:乙每天生产零件60个
教材补充例题 某车间有22名工人,每人每天可以生产1 200个螺钉或2 000个螺母,1个螺钉需要配2个螺母,为使每天生产的螺钉和螺母刚好配套,应安排生产螺钉和螺母的工人各多少名?
分析:
单日每人生产 个螺钉, 个螺母;
设每日生产螺钉人数为x,则每日生产螺母人数为 人;
每日生产螺钉 个,生产螺母 个;
螺钉和螺母之间的关系 ;
根据螺钉和螺母之间的关系可列方程为 .
2000(22-x)=2×1200x
1200
2000
(22-x)
1200x
2000(22-x)
或螺母数量是螺钉的2倍
螺钉数:螺母数= 1:2
解:设应安排 x 名工人生产螺钉,(22-x)名工人生
产螺母.依题意,得
2000(22-x)=2×1200x .
解方程,得 x=10.
所以 22-x=12.
答:应安排10名工人生产螺钉,12名工人生产螺母.
归纳:
1.分析配套问题时需要注意问题中所涉及的量的比例关系,
比如:1个螺钉需要配2个螺母可表示为螺钉数:螺母数= 1:2;
2.注意通过找到的比例关系列方程;
如:根据螺钉数:螺母数= 1:2
3.可以根据比例式的內项积等于外项积将含比的方程转化为我们熟悉的形式 .
工作量、工作效率、工作时间之间的关系:
(1)工作量=工作效率×工作时间,
工作时间=工作量÷工作效率,
工作效率=工作量÷工作时间;
(2)甲、乙合做的总工作量=甲的工作量+乙的工作量;
(3)甲、乙合做的工作时间=总工作量÷(甲的工作效率+乙的工作效率).
【归纳总结】
获取新知
列表法是分析调配问题数量关系的常用的方法.
随堂演练
1.某商场将一种商品以每件60元的价格售出,盈利20%,
那么该商品的进货价为每件( )
A.80元 B.72元
C.50元 D.36元
C
2. 某班学生分两组参加某项活动,甲组有26人,乙组有32人,后来由于活动需要,从甲组抽调了部分学生去乙组,结果乙组的人数比甲组人数的2倍还多1人.从甲组抽调了多少名学生去乙组?
解:设从甲组抽调了x名学生去乙组.
根据题意,得2(26-x)+1=32+x,解得x=7.
答:从甲组抽调了7名学生去乙组.
3.一件工作,甲单独做需要10小时完成,乙单独做需要15小
时完成,那么甲每小时完成总工作量的________,乙每小时完
成总工作量的________.若设甲、乙合作需要x小时完成,则
可列方程为________________,解得x=________.
1
—
10
1
—
15
x
— +
10
x
— = 1
15
6
4. 有一个加工茶杯的车间,平均每个工人每小时可以加工杯身12个,或者加工杯盖15个.1个杯身配1个杯盖,车间共有90人,则安排多少人加工杯身,才能使每小时加工的杯身和杯盖正好配套?
解:设安排x人加工杯身,
则加工杯盖的人数为________,
每小时加工杯身____个,杯盖__________个,
则可列方程为________________,
解得x=_____.
90-x
12x=15(90-x)
15(90-x)
12x
50
课堂总结
一元一次方程的应用
劳动力调配问题中的相等关系
调配前量的关系
调配后量的关系
工程问题
基本公式:工作量=工作效率×工作时间
相等关系:全部工作量=各部分工作量之和
同课章节目录
- 第1章 有理数
- 1.1 从自然数到有理数
- 1.2 数轴
- 1.3 绝对值
- 1.4 有理数大小比较
- 第2章 有理数的运算
- 2.1 有理数的加法
- 2.2 有理数的减法
- 2.3 有理数的乘法
- 2.4 有理数的除法
- 2.5 有理数的乘方
- 2.6 有理数的混合运算
- 2.7 近似数
- 第3章 实数
- 3.1 平方根
- 3.2 实数
- 3.3 立方根
- 3.4 实数的运算
- 第4章 代数式
- 4.1 用字母表示数
- 4.2 代数式
- 4.3 代数式的值
- 4.4 整式
- 4.5 合并同类项
- 4.6 整式的加减
- 第5章 一元一次方程
- 5.1 一元一次方程
- 5.2 等式的基本性质
- 5.3 一元一次方程的解法
- 5.4 一元一次方程的应用
- 第6章 图形的初步知识
- 6.1 几何图形
- 6.2 线段、射线和直线
- 6.3 线段的长短比较
- 6.4 线段的和差
- 6.5 角与角的度量
- 6.6 角的大小比较
- 6.7 角的和差
- 6.8 余角和补角
- 6.9 直线的相交
