浙教版数学七年级上册:6.4线段的和差 同步新授课件(共17张PPT)
文档属性
| 名称 | 浙教版数学七年级上册:6.4线段的和差 同步新授课件(共17张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 369.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-08 15:38:23 | ||
图片预览




文档简介
(共17张PPT)
第六章 图形的初步认识
6.4 线段的和差
情景导入
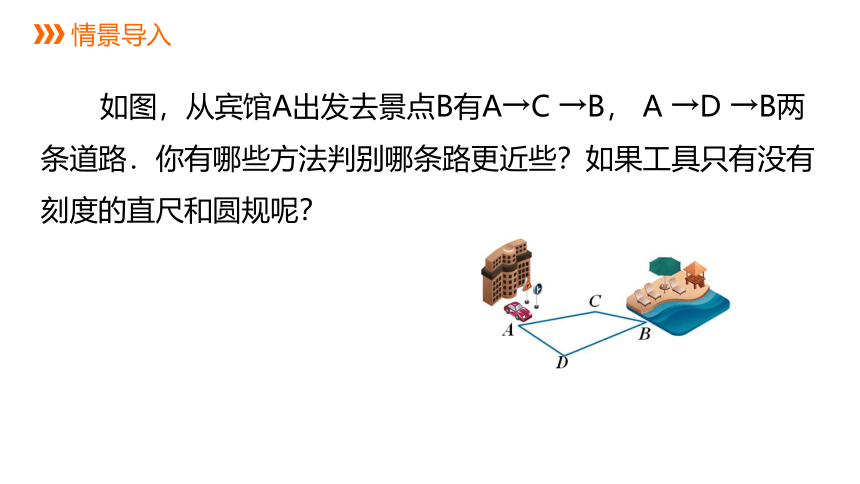
如图,从宾馆A出发去景点B有A→C →B, A →D →B两条道路.你有哪些方法判别哪条路更近些?如果工具只有没有刻度的直尺和圆规呢?
获取新知
如图,已知线段a=1.5 cm,b=2.5 cm,c=4 cm.
请议一议,a,b,c三条线段的长度之间有怎样的关系?
a+b=1.5+2.5=4,所以a+b=c.
c-a=4-1.5=2.5,所以c-a=b.
c-b=4-2.5=1.5,所以c-b=a.
如果一条线段的长度是另两条线段的长度的和,那么这条线段就叫做 __________________;如果一条线段的长度是另两条线段的长度的差,那么这条线段就叫做________________.
另两条线段的和
另两条线段的差
两条线段的和或差仍是一条线段.
线段c是线段a与b的和,记做___________;线段a是线段c与b的差,记做___________.
c=a+b
a=c-b
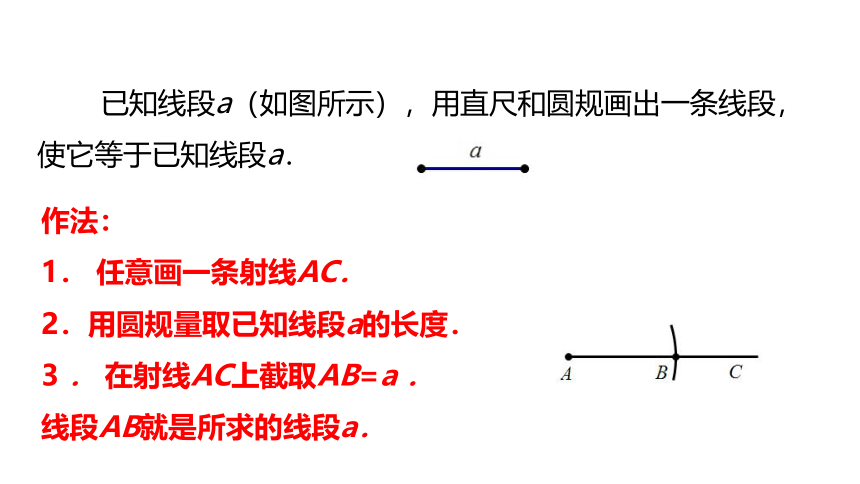
已知线段a(如图所示),用直尺和圆规画出一条线段,使它等于已知线段a.
作法:
1. 任意画一条射线AC.
2.用圆规量取已知线段a的长度.
3 . 在射线AC上截取AB=a .
线段AB就是所求的线段a.
线段的和差从数量上看实质是两条线段的_______的和差;
线段的和差从图形上看反映了线段之间_____________的关系.
长度
部分与整体
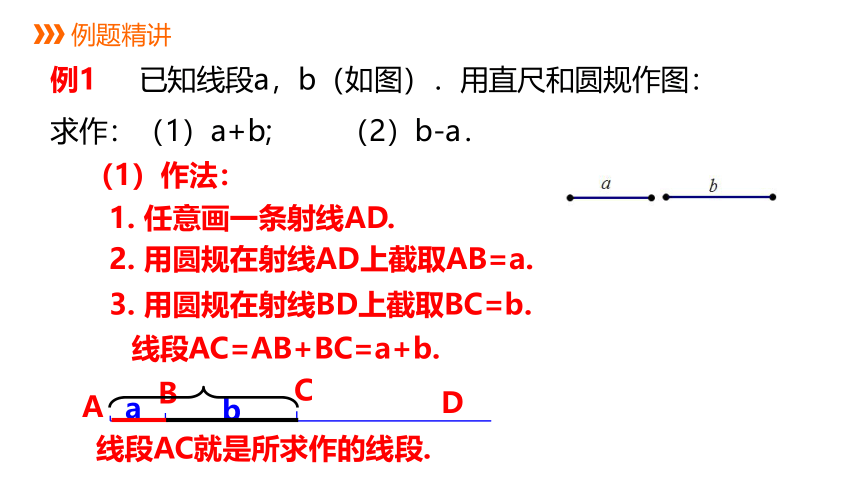
例1 已知线段a,b(如图).用直尺和圆规作图:求作:(1)a+b; (2)b-a.
b
(1)作法:
1. 任意画一条射线AD.
2. 用圆规在射线AD上截取AB=a.
3. 用圆规在射线BD上截取BC=b.
a
A
D
B
C
线段AC就是所求作的线段.
例题精讲
线段AC=AB+BC=a+b.
(2)作法如图:
1.作线段 AB=b.
2.在线段AB上截取AC=a.
线段BC=AB-AC=b-a,线段BC就是所求作的线段.
如图,点C把线段AB分成相等的两条线段AC与BC,点C叫做线段AB的中点.
A C B
几何语言:
∵点C是线段AB的中点,∴AC=BC.
∵点C是线段AB的中点,∴AB=2AC=2BC,
∵点C是线段AB的中点,∴AC=BC= AB.
如图:如果点C是线段AB的中点,那么就有AC=BC= AB .
AB=2AC=2BC.
A C B
例2 如图,P是线段AB的中点,点C,D把线段AB三等分.
已知线段CP的长为1.5 cm,求线段AB的长.
分析 如果能得到线段CP与线段AB之间的长度比,就能求出线段AB的长.
解:∵点P是线段AB的中点,
∴AP=BP= AB.
∵点C,D把线段AB三等分,
∴AC=CD=DB= AB.
∴ AB- AB=CP,即CP = AB .
∴AB=6CP=6×1.5=9(cm) .
答:线段AB的长为9 cm.
随堂演练
1.如图,看图填空:
(1)AC=AD-________;
(2)BC+CD=________-AB.
CD
AD
2.如图,AB=CD,则AC与BD的大小关系是( )
A.AC>BD B.AC<BD
C
C.AC=BD D.无法确定
3.如图,C,D是线段AB上的两点,D是线段AC的中点.若AB=10 cm,BC=4 cm,则AD的长为( )
A.2 cm B.3 cm C.4 cm D.6 cm
B
4.已知,如图,B,C两点把线段AD分成2:5:3三部分,M为AD的中点,BM=6,求CM和AD的长.
D
A
C
B
M
AD=10x=20 .
解:设AB=2x,BC=5x,CD=3x,
所以AD=AB+BC+CD=10x.
因为M是AD的中点,
所以AM=MD=5x,
所以BM=AM-AB=3x.
因为BM=6,
即3x=6,所以x=2.
故CM=MD-CD=2x=4,
线段的和与差
线段的和与差
线段的中点
如图,点C在线段AB上,则AB=AC+BC,AC=AB-BC.
如图,线段AB上有一点M,把线段 AB分成两条线段AM与MB.如果AM=MB,那么M就叫做线段AB的中点.
A
M
B
课堂小结
第六章 图形的初步认识
6.4 线段的和差
情景导入
如图,从宾馆A出发去景点B有A→C →B, A →D →B两条道路.你有哪些方法判别哪条路更近些?如果工具只有没有刻度的直尺和圆规呢?
获取新知
如图,已知线段a=1.5 cm,b=2.5 cm,c=4 cm.
请议一议,a,b,c三条线段的长度之间有怎样的关系?
a+b=1.5+2.5=4,所以a+b=c.
c-a=4-1.5=2.5,所以c-a=b.
c-b=4-2.5=1.5,所以c-b=a.
如果一条线段的长度是另两条线段的长度的和,那么这条线段就叫做 __________________;如果一条线段的长度是另两条线段的长度的差,那么这条线段就叫做________________.
另两条线段的和
另两条线段的差
两条线段的和或差仍是一条线段.
线段c是线段a与b的和,记做___________;线段a是线段c与b的差,记做___________.
c=a+b
a=c-b
已知线段a(如图所示),用直尺和圆规画出一条线段,使它等于已知线段a.
作法:
1. 任意画一条射线AC.
2.用圆规量取已知线段a的长度.
3 . 在射线AC上截取AB=a .
线段AB就是所求的线段a.
线段的和差从数量上看实质是两条线段的_______的和差;
线段的和差从图形上看反映了线段之间_____________的关系.
长度
部分与整体
例1 已知线段a,b(如图).用直尺和圆规作图:求作:(1)a+b; (2)b-a.
b
(1)作法:
1. 任意画一条射线AD.
2. 用圆规在射线AD上截取AB=a.
3. 用圆规在射线BD上截取BC=b.
a
A
D
B
C
线段AC就是所求作的线段.
例题精讲
线段AC=AB+BC=a+b.
(2)作法如图:
1.作线段 AB=b.
2.在线段AB上截取AC=a.
线段BC=AB-AC=b-a,线段BC就是所求作的线段.
如图,点C把线段AB分成相等的两条线段AC与BC,点C叫做线段AB的中点.
A C B
几何语言:
∵点C是线段AB的中点,∴AC=BC.
∵点C是线段AB的中点,∴AB=2AC=2BC,
∵点C是线段AB的中点,∴AC=BC= AB.
如图:如果点C是线段AB的中点,那么就有AC=BC= AB .
AB=2AC=2BC.
A C B
例2 如图,P是线段AB的中点,点C,D把线段AB三等分.
已知线段CP的长为1.5 cm,求线段AB的长.
分析 如果能得到线段CP与线段AB之间的长度比,就能求出线段AB的长.
解:∵点P是线段AB的中点,
∴AP=BP= AB.
∵点C,D把线段AB三等分,
∴AC=CD=DB= AB.
∴ AB- AB=CP,即CP = AB .
∴AB=6CP=6×1.5=9(cm) .
答:线段AB的长为9 cm.
随堂演练
1.如图,看图填空:
(1)AC=AD-________;
(2)BC+CD=________-AB.
CD
AD
2.如图,AB=CD,则AC与BD的大小关系是( )
A.AC>BD B.AC<BD
C
C.AC=BD D.无法确定
3.如图,C,D是线段AB上的两点,D是线段AC的中点.若AB=10 cm,BC=4 cm,则AD的长为( )
A.2 cm B.3 cm C.4 cm D.6 cm
B
4.已知,如图,B,C两点把线段AD分成2:5:3三部分,M为AD的中点,BM=6,求CM和AD的长.
D
A
C
B
M
AD=10x=20 .
解:设AB=2x,BC=5x,CD=3x,
所以AD=AB+BC+CD=10x.
因为M是AD的中点,
所以AM=MD=5x,
所以BM=AM-AB=3x.
因为BM=6,
即3x=6,所以x=2.
故CM=MD-CD=2x=4,
线段的和与差
线段的和与差
线段的中点
如图,点C在线段AB上,则AB=AC+BC,AC=AB-BC.
如图,线段AB上有一点M,把线段 AB分成两条线段AM与MB.如果AM=MB,那么M就叫做线段AB的中点.
A
M
B
课堂小结
同课章节目录
- 第1章 有理数
- 1.1 从自然数到有理数
- 1.2 数轴
- 1.3 绝对值
- 1.4 有理数大小比较
- 第2章 有理数的运算
- 2.1 有理数的加法
- 2.2 有理数的减法
- 2.3 有理数的乘法
- 2.4 有理数的除法
- 2.5 有理数的乘方
- 2.6 有理数的混合运算
- 2.7 近似数
- 第3章 实数
- 3.1 平方根
- 3.2 实数
- 3.3 立方根
- 3.4 实数的运算
- 第4章 代数式
- 4.1 用字母表示数
- 4.2 代数式
- 4.3 代数式的值
- 4.4 整式
- 4.5 合并同类项
- 4.6 整式的加减
- 第5章 一元一次方程
- 5.1 一元一次方程
- 5.2 等式的基本性质
- 5.3 一元一次方程的解法
- 5.4 一元一次方程的应用
- 第6章 图形的初步知识
- 6.1 几何图形
- 6.2 线段、射线和直线
- 6.3 线段的长短比较
- 6.4 线段的和差
- 6.5 角与角的度量
- 6.6 角的大小比较
- 6.7 角的和差
- 6.8 余角和补角
- 6.9 直线的相交
