浙教版数学七年级上册:6.6角的大小比较 同步新授课件(共14张PPT)
文档属性
| 名称 | 浙教版数学七年级上册:6.6角的大小比较 同步新授课件(共14张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 271.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-08 15:39:14 | ||
图片预览




文档简介
(共14张PPT)
第六章 图形的初步认识
6.6 角的大小比较
D
C
B
线段长短的比较方法.
(1) 度量法
(2) 叠合法
将其中一条线段“移”到另一条线段上,使其一端点与另一线段的一端点重合,然后观察两条线段另外两个端点的位置作比较.
(A)
C D
A B
尺规作图
知识回顾
复习
C
D
1. 若点 A 与点 C 重合,点 B 落在C,D之间,那么 AB CD.
(A)
B
<
叠合法结论:
C
D
A
B
B
(A)
2. 若点 A 与点 C 重合,点 B 与点 D ,那么 AB = CD.
3. 若点 A 与点 C 重合,点 B 落在 CD 的延长线上,那么 AB_____CD.
重合
>
B
A
B
A
C
D
(A)
(B)
获取新知
A
B
C
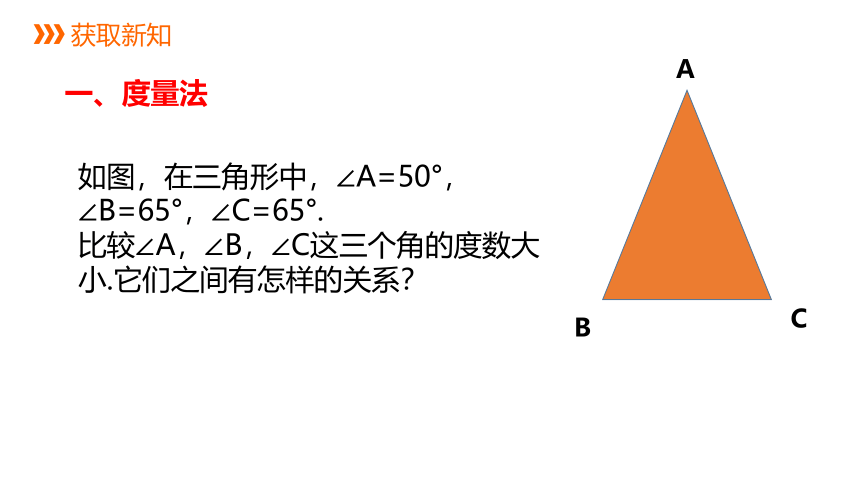
如图,在三角形中,∠A=50°,∠B=65°,∠C=65°.
比较∠A,∠B,∠C这三个角的度数大小.它们之间有怎样的关系?
一、度量法
一般地,如果两个角的度数相等,那么我们就说这两个角相等,∠B与∠C相等,记作∠B=∠C
如果两个角的度数不相等,那么我们就说度数较大的角较大,∠B大于∠A,记作∠B>∠A
也可以说成∠A小于∠B,记作∠A<∠B
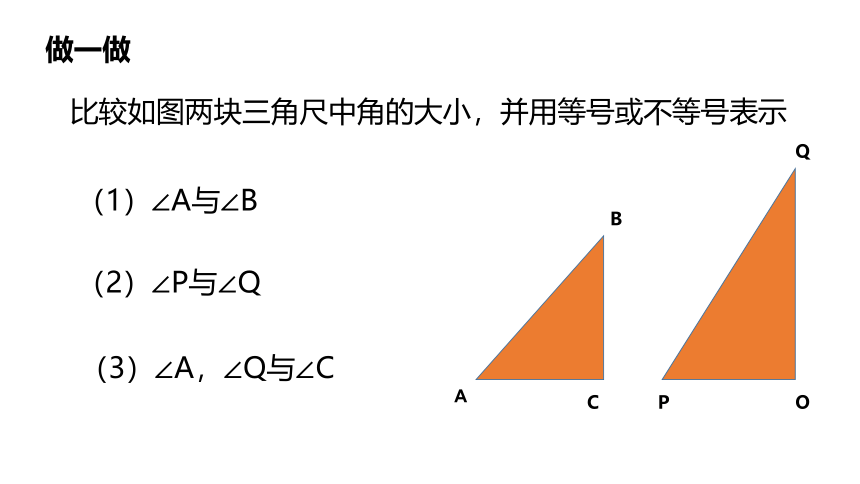
做一做
比较如图两块三角尺中角的大小,并用等号或不等号表示
(1)∠A与∠B
(2)∠P与∠Q
(3)∠A,∠Q与∠C
A
B
C
P
O
Q
例题精讲
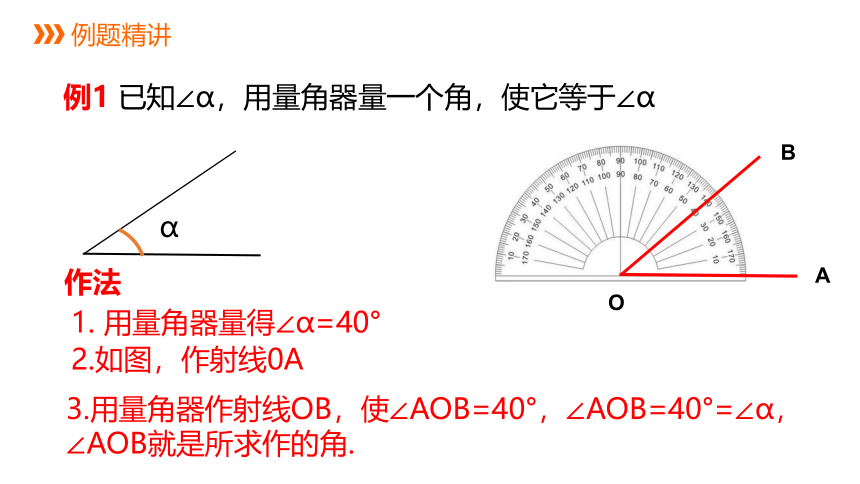
例1 已知∠α,用量角器量一个角,使它等于∠α
1. 用量角器量得∠α=40°
2.如图,作射线0A
3.用量角器作射线OB,使∠AOB=40°,∠AOB=40°=∠α,∠AOB就是所求作的角.
O
A
B
α
作法
1.将两个角的顶点及一边重合
2.两个角的另一边落在重合一边的同侧
3.由两个角的另一边的位置确定两个角的大小
二. 叠合法
A
B
O
(O' )
B'
(A' )
A
B
O
∠AOB<∠A'O'B'
∠AOB =∠A'O'B'
(O' )
(B' )
(A' )
∠AOB>∠A'O'B'
A
B
O
(O' )
B'
(A' )
等于90°的角是直角,小于直角的角是锐角,大于直角而小于平角的角是钝角.
例2 如图,点A、O、E在一条直线上,∠AOC=90°,∠BOD=90°,解答下列问题:
(1)比较∠AOB,∠AOC,∠AOD,∠AOE的大小
(2)找出图中的直角、钝角和锐角
解 (1)由图可以看出:
∠AOB<∠AOC<∠AOD<∠AOE
(2)图中的直角有∠AOC,∠BOD,∠COE; 锐角有∠AOB,∠BOC,∠COD,∠DOE;
钝角有∠AOD,∠BOE
例题讲解
随堂演练
1.已知∠AOB是锐角,则下列表述正确的是( )
A.0°<∠AOB<45° B.∠AOB>45°
C.0°<∠AOB<90° D.∠AOB>90°
C
2.下列语句中正确的是( )
A.小于平角的角是锐角
B.大于直角的角是钝角
C.等于90°的角是直角
D.大于锐角的角是钝角
C
3.如图,用“>”或“<”填空.
∠AOB______∠AOC,∠POR______∠POQ.
<
>
角的大小
角的比较
作一个角等于已知角
度量法:用量角器分别测量出两个角的度数,通过度数大小来判断两个角的大小.
叠合法:移动一个角使它的顶点和一条边与另一个角的顶点和一边重合,而其余的边在重合边的同侧,通过不重合两边的位置来判断两个角的大小.
作一个角等于已知角的两种方法:
一是用量角器作图;
二是用直尺和圆规作图(尺规作图).
课堂小结
第六章 图形的初步认识
6.6 角的大小比较
D
C
B
线段长短的比较方法.
(1) 度量法
(2) 叠合法
将其中一条线段“移”到另一条线段上,使其一端点与另一线段的一端点重合,然后观察两条线段另外两个端点的位置作比较.
(A)
C D
A B
尺规作图
知识回顾
复习
C
D
1. 若点 A 与点 C 重合,点 B 落在C,D之间,那么 AB CD.
(A)
B
<
叠合法结论:
C
D
A
B
B
(A)
2. 若点 A 与点 C 重合,点 B 与点 D ,那么 AB = CD.
3. 若点 A 与点 C 重合,点 B 落在 CD 的延长线上,那么 AB_____CD.
重合
>
B
A
B
A
C
D
(A)
(B)
获取新知
A
B
C
如图,在三角形中,∠A=50°,∠B=65°,∠C=65°.
比较∠A,∠B,∠C这三个角的度数大小.它们之间有怎样的关系?
一、度量法
一般地,如果两个角的度数相等,那么我们就说这两个角相等,∠B与∠C相等,记作∠B=∠C
如果两个角的度数不相等,那么我们就说度数较大的角较大,∠B大于∠A,记作∠B>∠A
也可以说成∠A小于∠B,记作∠A<∠B
做一做
比较如图两块三角尺中角的大小,并用等号或不等号表示
(1)∠A与∠B
(2)∠P与∠Q
(3)∠A,∠Q与∠C
A
B
C
P
O
Q
例题精讲
例1 已知∠α,用量角器量一个角,使它等于∠α
1. 用量角器量得∠α=40°
2.如图,作射线0A
3.用量角器作射线OB,使∠AOB=40°,∠AOB=40°=∠α,∠AOB就是所求作的角.
O
A
B
α
作法
1.将两个角的顶点及一边重合
2.两个角的另一边落在重合一边的同侧
3.由两个角的另一边的位置确定两个角的大小
二. 叠合法
A
B
O
(O' )
B'
(A' )
A
B
O
∠AOB<∠A'O'B'
∠AOB =∠A'O'B'
(O' )
(B' )
(A' )
∠AOB>∠A'O'B'
A
B
O
(O' )
B'
(A' )
等于90°的角是直角,小于直角的角是锐角,大于直角而小于平角的角是钝角.
例2 如图,点A、O、E在一条直线上,∠AOC=90°,∠BOD=90°,解答下列问题:
(1)比较∠AOB,∠AOC,∠AOD,∠AOE的大小
(2)找出图中的直角、钝角和锐角
解 (1)由图可以看出:
∠AOB<∠AOC<∠AOD<∠AOE
(2)图中的直角有∠AOC,∠BOD,∠COE; 锐角有∠AOB,∠BOC,∠COD,∠DOE;
钝角有∠AOD,∠BOE
例题讲解
随堂演练
1.已知∠AOB是锐角,则下列表述正确的是( )
A.0°<∠AOB<45° B.∠AOB>45°
C.0°<∠AOB<90° D.∠AOB>90°
C
2.下列语句中正确的是( )
A.小于平角的角是锐角
B.大于直角的角是钝角
C.等于90°的角是直角
D.大于锐角的角是钝角
C
3.如图,用“>”或“<”填空.
∠AOB______∠AOC,∠POR______∠POQ.
<
>
角的大小
角的比较
作一个角等于已知角
度量法:用量角器分别测量出两个角的度数,通过度数大小来判断两个角的大小.
叠合法:移动一个角使它的顶点和一条边与另一个角的顶点和一边重合,而其余的边在重合边的同侧,通过不重合两边的位置来判断两个角的大小.
作一个角等于已知角的两种方法:
一是用量角器作图;
二是用直尺和圆规作图(尺规作图).
课堂小结
同课章节目录
- 第1章 有理数
- 1.1 从自然数到有理数
- 1.2 数轴
- 1.3 绝对值
- 1.4 有理数大小比较
- 第2章 有理数的运算
- 2.1 有理数的加法
- 2.2 有理数的减法
- 2.3 有理数的乘法
- 2.4 有理数的除法
- 2.5 有理数的乘方
- 2.6 有理数的混合运算
- 2.7 近似数
- 第3章 实数
- 3.1 平方根
- 3.2 实数
- 3.3 立方根
- 3.4 实数的运算
- 第4章 代数式
- 4.1 用字母表示数
- 4.2 代数式
- 4.3 代数式的值
- 4.4 整式
- 4.5 合并同类项
- 4.6 整式的加减
- 第5章 一元一次方程
- 5.1 一元一次方程
- 5.2 等式的基本性质
- 5.3 一元一次方程的解法
- 5.4 一元一次方程的应用
- 第6章 图形的初步知识
- 6.1 几何图形
- 6.2 线段、射线和直线
- 6.3 线段的长短比较
- 6.4 线段的和差
- 6.5 角与角的度量
- 6.6 角的大小比较
- 6.7 角的和差
- 6.8 余角和补角
- 6.9 直线的相交
