浙教版数学七年级上册:3.2实数 同步新授课件(共22张PPT)
文档属性
| 名称 | 浙教版数学七年级上册:3.2实数 同步新授课件(共22张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 466.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-08 15:49:05 | ||
图片预览






文档简介
(共22张PPT)
第三章 实数
3.2 实数
知识回顾
平方根的性质:
一个正数有两个平方根,它们互为相反数,0的平方根是0,负数没有平方根;
有理数分为整数和分数
除了有理数还有别的数吗?
获取新知
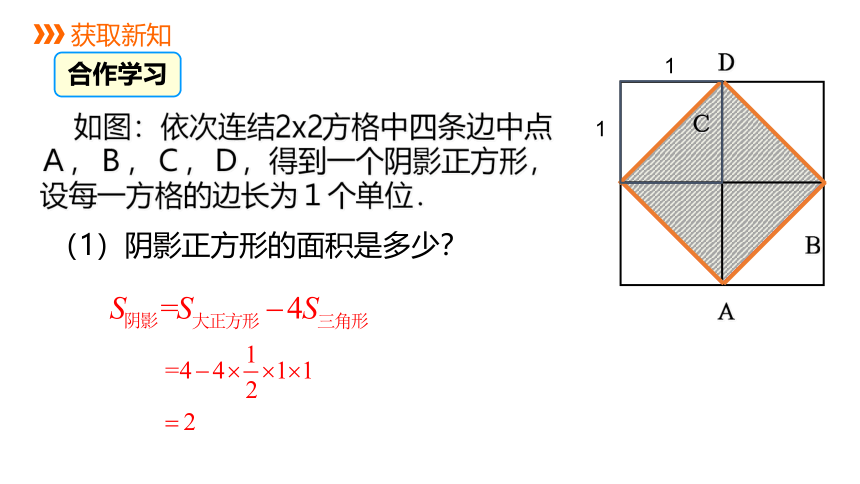
如图:依次连结2x2方格中四条边中点A,B,C,D,得到一个阴影正方形,设每一方格的边长为1个单位.
1
1
A
B
C
D
(1)阴影正方形的面积是多少?
合作学习
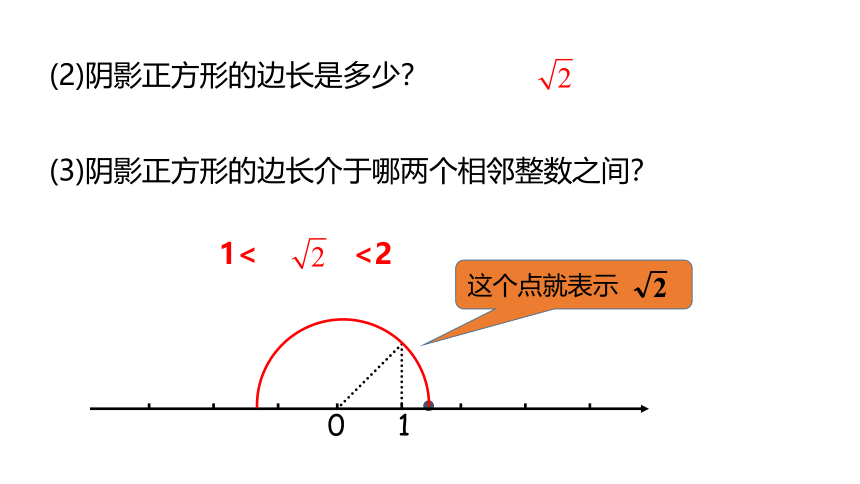
(2)阴影正方形的边长是多少?
(3)阴影正方形的边长介于哪两个相邻整数之间?
1< <2
0
1
这个点就表示
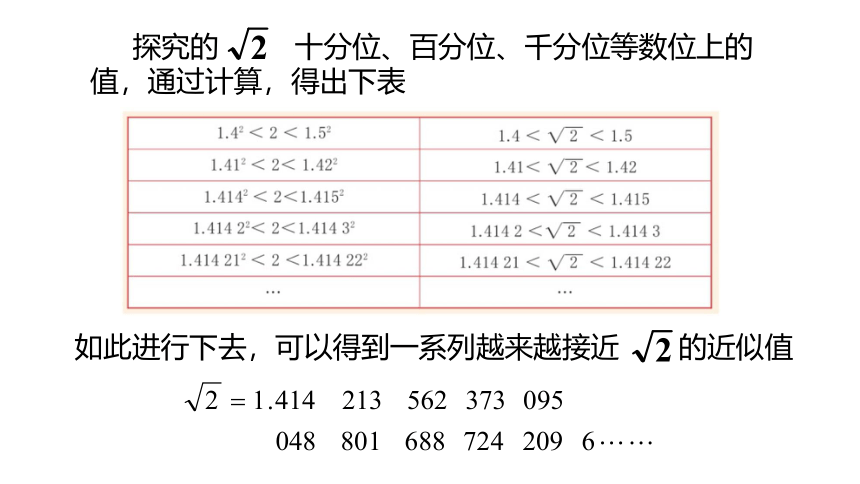
探究的 十分位、百分位、千分位等数位上的值,通过计算,得出下表
如此进行下去,可以得到一系列越来越接近 的近似值
既不是有限小数,也不是无限循环小数(不能化为分数)
我们把这种无限不循环小数叫做无理数.
= 3.141 592 653 589 793 238 46…
=1.732 050 807 568 877 293 527 446 341 505 872 366 9...
任意写一个无限不循环小数,如1.010 010 001...(两个“1”之间的依次多一个“0”),它也是无理数
解:
有理数是:
无理数是:
例1 判断下列数哪些是有理数?哪些是无理数?
例题讲解
归纳:无理数的特征:
1.圆周率π及一些含有π的数
2.开方开不尽的数,如: 等
3.有一定的规律,但不循环的无限小数,如:
定义:有理数和无理数统称为实数.
实数的概念
实数如何进行分类呢?
负有理数
1.按定义分类:
实数
有理数
无理数
正有理数
正有理数
负有理数
无限不循环小数
零
有限小数和无限循环小数
正无理数
2.按性质分类:
实数
正实数
负实数
正有理数
负无理数
负有理数
零
把数从有理数扩充到实数以后,有理数中的相反数和绝对值的概念同样适用。
例如: 和 互为相反数
(1.) 的相反数是
(2) =
做一做
-
(3) 一个数的绝对值是 ,则这个数是
0
1
-1
A
C
如图:OA=OB=OC,数轴上A、C对应的数是什么
B
在实数范围内,每一个实数都可以用数轴上的点来表示;反过来,数轴上的每一个点都表示一个实数.我们说实数和数轴上的点是一一对应的.
实数和数轴上的点是一一对应的.
在数轴上表示的两个实数,
右边的数总比左边的数大.
有理数的大小比较法则也适用于实数:
例2 把下列实数表示在数轴上,并比较它们的大小(用“<”连接).
例题讲解
-π,
解 把 表示在数轴上,如图:
-π,
0
1
2
-1
-2
3
1.5
-3
-π
所以 < < <
-π
随堂演练
1.下列说法正确的是( )
A.无理数都是实数,实数都是无理数
B.无限小数都是无理数
C.无理数是无限小数
D.不带根号的数一定是有理数
C
2.如图,在数轴上的点A,B,C,D中,与表示
的点距离最近的是( )
A.点A B.点B
C.点C D.点D
B
3. 是 的( )
A.相反数 B.倒数
C.负平方根 D.绝对值
4. 2- 的绝对值是( )
A.2-
B. -2
C.2+
D.±(2- )
A
B
5.[2018·宁波期中]在0,-2, ,1中,最小
的实数是( )
A. B.0
C.-2 D.1
C
与数轴上的点一一对应
实数
是不是无限不循环小数
与0比较大小
基本类型
_____________
有规律但不循环小数(无限不循环小数 )
化简后含π的数
是
正实数
0
负实数
否
有理数
无理数
开方开不尽的数
课堂小结
第三章 实数
3.2 实数
知识回顾
平方根的性质:
一个正数有两个平方根,它们互为相反数,0的平方根是0,负数没有平方根;
有理数分为整数和分数
除了有理数还有别的数吗?
获取新知
如图:依次连结2x2方格中四条边中点A,B,C,D,得到一个阴影正方形,设每一方格的边长为1个单位.
1
1
A
B
C
D
(1)阴影正方形的面积是多少?
合作学习
(2)阴影正方形的边长是多少?
(3)阴影正方形的边长介于哪两个相邻整数之间?
1< <2
0
1
这个点就表示
探究的 十分位、百分位、千分位等数位上的值,通过计算,得出下表
如此进行下去,可以得到一系列越来越接近 的近似值
既不是有限小数,也不是无限循环小数(不能化为分数)
我们把这种无限不循环小数叫做无理数.
= 3.141 592 653 589 793 238 46…
=1.732 050 807 568 877 293 527 446 341 505 872 366 9...
任意写一个无限不循环小数,如1.010 010 001...(两个“1”之间的依次多一个“0”),它也是无理数
解:
有理数是:
无理数是:
例1 判断下列数哪些是有理数?哪些是无理数?
例题讲解
归纳:无理数的特征:
1.圆周率π及一些含有π的数
2.开方开不尽的数,如: 等
3.有一定的规律,但不循环的无限小数,如:
定义:有理数和无理数统称为实数.
实数的概念
实数如何进行分类呢?
负有理数
1.按定义分类:
实数
有理数
无理数
正有理数
正有理数
负有理数
无限不循环小数
零
有限小数和无限循环小数
正无理数
2.按性质分类:
实数
正实数
负实数
正有理数
负无理数
负有理数
零
把数从有理数扩充到实数以后,有理数中的相反数和绝对值的概念同样适用。
例如: 和 互为相反数
(1.) 的相反数是
(2) =
做一做
-
(3) 一个数的绝对值是 ,则这个数是
0
1
-1
A
C
如图:OA=OB=OC,数轴上A、C对应的数是什么
B
在实数范围内,每一个实数都可以用数轴上的点来表示;反过来,数轴上的每一个点都表示一个实数.我们说实数和数轴上的点是一一对应的.
实数和数轴上的点是一一对应的.
在数轴上表示的两个实数,
右边的数总比左边的数大.
有理数的大小比较法则也适用于实数:
例2 把下列实数表示在数轴上,并比较它们的大小(用“<”连接).
例题讲解
-π,
解 把 表示在数轴上,如图:
-π,
0
1
2
-1
-2
3
1.5
-3
-π
所以 < < <
-π
随堂演练
1.下列说法正确的是( )
A.无理数都是实数,实数都是无理数
B.无限小数都是无理数
C.无理数是无限小数
D.不带根号的数一定是有理数
C
2.如图,在数轴上的点A,B,C,D中,与表示
的点距离最近的是( )
A.点A B.点B
C.点C D.点D
B
3. 是 的( )
A.相反数 B.倒数
C.负平方根 D.绝对值
4. 2- 的绝对值是( )
A.2-
B. -2
C.2+
D.±(2- )
A
B
5.[2018·宁波期中]在0,-2, ,1中,最小
的实数是( )
A. B.0
C.-2 D.1
C
与数轴上的点一一对应
实数
是不是无限不循环小数
与0比较大小
基本类型
_____________
有规律但不循环小数(无限不循环小数 )
化简后含π的数
是
正实数
0
负实数
否
有理数
无理数
开方开不尽的数
课堂小结
同课章节目录
- 第1章 有理数
- 1.1 从自然数到有理数
- 1.2 数轴
- 1.3 绝对值
- 1.4 有理数大小比较
- 第2章 有理数的运算
- 2.1 有理数的加法
- 2.2 有理数的减法
- 2.3 有理数的乘法
- 2.4 有理数的除法
- 2.5 有理数的乘方
- 2.6 有理数的混合运算
- 2.7 近似数
- 第3章 实数
- 3.1 平方根
- 3.2 实数
- 3.3 立方根
- 3.4 实数的运算
- 第4章 代数式
- 4.1 用字母表示数
- 4.2 代数式
- 4.3 代数式的值
- 4.4 整式
- 4.5 合并同类项
- 4.6 整式的加减
- 第5章 一元一次方程
- 5.1 一元一次方程
- 5.2 等式的基本性质
- 5.3 一元一次方程的解法
- 5.4 一元一次方程的应用
- 第6章 图形的初步知识
- 6.1 几何图形
- 6.2 线段、射线和直线
- 6.3 线段的长短比较
- 6.4 线段的和差
- 6.5 角与角的度量
- 6.6 角的大小比较
- 6.7 角的和差
- 6.8 余角和补角
- 6.9 直线的相交
