浙教版数学七年级上册:3.3立方根 同步新授课件(共14张PPT)
文档属性
| 名称 | 浙教版数学七年级上册:3.3立方根 同步新授课件(共14张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-08 00:00:00 | ||
图片预览






文档简介
(共14张PPT)
第三章 实数
3.3 立方根
知识回顾
一般地,如果一个数x的平方等于a,即x2=a,那么这个数x叫做a的平方根或二次方根. 0的平方根是0.
a的平方根记作: .
获取新知
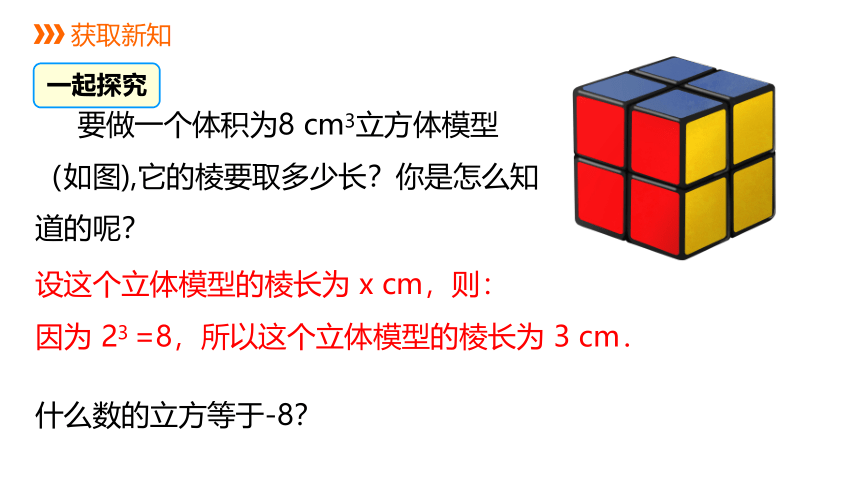
要做一个体积为8 cm3立方体模型(如图),它的棱要取多少长?你是怎么知道的呢?
什么数的立方等于-8?
设这个立体模型的棱长为 x cm,则:
因为 23 =8,所以这个立体模型的棱长为 3 cm.
一起探究
一般地,一个数的立方等于a,这个数就叫做a的立方根,也叫a的三次方根.
根指数
被开方数
3是根指数,不能省略.
读作:三次根号 a.
例如,23=8,其中2是8的立方根,即 ;(-2)3=-8,其中-2是-8的立方根,即 .
知识归纳
注意
求一个数的立方根的运算,叫做开立方.
类似于开平方是平方运算的逆运算,开立方也是立方运算的逆运算,因此,可以运用平方运算求一个数的平方根.
例1 求下列各数的立方根:
(1)27;(2)-27;(3) ; (4) -0.064 ; (5)0.
解:(1)∵ 33=27,
∴ 27的立方根是3,
∴ -27的立方根是-3,
即 .
即 .
说明:互为相反数的数的立方根也互为相反数.
(2)∵ (-3)3=-27,
(3)∵ ,
∴ 的立方根是 ,
即 .
(4)∵ (-0.4)3=-0.064,
∴ -0.064的立方根是-0.4,
即 .
(5)∵ 03=0,
∴ 0的立方根是0,
即 .
一般地,我们有以下事实:
一个正数有一个正的立方根;
一个负数有一个负的立方根;
0的立方根是0
知识归纳
例2 计算:
(1) ; (2) .
解:(1) ;
(2) .
知识归纳
平方根和立方根性质的对比:
被开方数 平方根 立方根
正数
负数
零
有两个,互为相反数
有一个,是正数
无平方根
零
有一个,是负数
零
随堂演练
1.(1)因为(____)3=8,所以8的立方根是____,用数
学式子表示为____________;
(2)因为(____)3=-64,所以-64的立方根是____,
用数学式子表示为______________;
(3)0的立方根是________.
2
2
-4
-4
0
2.下列说法正确的是( )
A.一个数总大于它的立方根
B.负数没有立方根
C.任何非零数都和它的立方根的符号相同
D.正数有两个立方根
C
3.一个长方体音箱,长是宽的2倍,宽和高相等,
它的体积是54000 cm3.这个音箱的长是( )
A.30 cm B.60 cm
C.300 cm D.600 cm
B
立方根
定义
一个数的立方等于a,这个数就叫做a的立方根
表示方法
基本性质
分类思想
一个正数有________
正的立方根
0的立方根是_______
一个负数有________
负的立方根
一个
0
一个
课堂小结
第三章 实数
3.3 立方根
知识回顾
一般地,如果一个数x的平方等于a,即x2=a,那么这个数x叫做a的平方根或二次方根. 0的平方根是0.
a的平方根记作: .
获取新知
要做一个体积为8 cm3立方体模型(如图),它的棱要取多少长?你是怎么知道的呢?
什么数的立方等于-8?
设这个立体模型的棱长为 x cm,则:
因为 23 =8,所以这个立体模型的棱长为 3 cm.
一起探究
一般地,一个数的立方等于a,这个数就叫做a的立方根,也叫a的三次方根.
根指数
被开方数
3是根指数,不能省略.
读作:三次根号 a.
例如,23=8,其中2是8的立方根,即 ;(-2)3=-8,其中-2是-8的立方根,即 .
知识归纳
注意
求一个数的立方根的运算,叫做开立方.
类似于开平方是平方运算的逆运算,开立方也是立方运算的逆运算,因此,可以运用平方运算求一个数的平方根.
例1 求下列各数的立方根:
(1)27;(2)-27;(3) ; (4) -0.064 ; (5)0.
解:(1)∵ 33=27,
∴ 27的立方根是3,
∴ -27的立方根是-3,
即 .
即 .
说明:互为相反数的数的立方根也互为相反数.
(2)∵ (-3)3=-27,
(3)∵ ,
∴ 的立方根是 ,
即 .
(4)∵ (-0.4)3=-0.064,
∴ -0.064的立方根是-0.4,
即 .
(5)∵ 03=0,
∴ 0的立方根是0,
即 .
一般地,我们有以下事实:
一个正数有一个正的立方根;
一个负数有一个负的立方根;
0的立方根是0
知识归纳
例2 计算:
(1) ; (2) .
解:(1) ;
(2) .
知识归纳
平方根和立方根性质的对比:
被开方数 平方根 立方根
正数
负数
零
有两个,互为相反数
有一个,是正数
无平方根
零
有一个,是负数
零
随堂演练
1.(1)因为(____)3=8,所以8的立方根是____,用数
学式子表示为____________;
(2)因为(____)3=-64,所以-64的立方根是____,
用数学式子表示为______________;
(3)0的立方根是________.
2
2
-4
-4
0
2.下列说法正确的是( )
A.一个数总大于它的立方根
B.负数没有立方根
C.任何非零数都和它的立方根的符号相同
D.正数有两个立方根
C
3.一个长方体音箱,长是宽的2倍,宽和高相等,
它的体积是54000 cm3.这个音箱的长是( )
A.30 cm B.60 cm
C.300 cm D.600 cm
B
立方根
定义
一个数的立方等于a,这个数就叫做a的立方根
表示方法
基本性质
分类思想
一个正数有________
正的立方根
0的立方根是_______
一个负数有________
负的立方根
一个
0
一个
课堂小结
同课章节目录
- 第1章 有理数
- 1.1 从自然数到有理数
- 1.2 数轴
- 1.3 绝对值
- 1.4 有理数大小比较
- 第2章 有理数的运算
- 2.1 有理数的加法
- 2.2 有理数的减法
- 2.3 有理数的乘法
- 2.4 有理数的除法
- 2.5 有理数的乘方
- 2.6 有理数的混合运算
- 2.7 近似数
- 第3章 实数
- 3.1 平方根
- 3.2 实数
- 3.3 立方根
- 3.4 实数的运算
- 第4章 代数式
- 4.1 用字母表示数
- 4.2 代数式
- 4.3 代数式的值
- 4.4 整式
- 4.5 合并同类项
- 4.6 整式的加减
- 第5章 一元一次方程
- 5.1 一元一次方程
- 5.2 等式的基本性质
- 5.3 一元一次方程的解法
- 5.4 一元一次方程的应用
- 第6章 图形的初步知识
- 6.1 几何图形
- 6.2 线段、射线和直线
- 6.3 线段的长短比较
- 6.4 线段的和差
- 6.5 角与角的度量
- 6.6 角的大小比较
- 6.7 角的和差
- 6.8 余角和补角
- 6.9 直线的相交
