浙教版数学八年级上册 3.2 不等式的基本性质 同步课件(共24张PPT)
文档属性
| 名称 | 浙教版数学八年级上册 3.2 不等式的基本性质 同步课件(共24张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 310.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-08 19:27:56 | ||
图片预览





文档简介
(共24张PPT)
第三章 一元一次不等式
3.2 不等式的基本性质
【思考】
判断下列说法是否正确:
1.若a=b,b=c,则 a=c
2.若a=b,则 a+1=b+1
3.若a=b,则 3a=3b
等式的基本性质
知识回顾
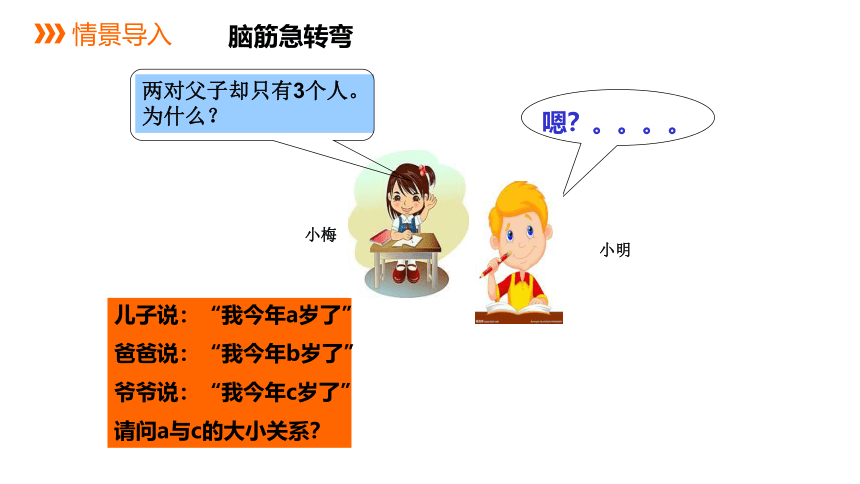
两对父子却只有3个人。为什么?
嗯?。。。。
儿子说:“我今年a岁了”
爸爸说:“我今年b岁了”
爷爷说:“我今年c岁了”
请问a与c的大小关系?
小明
小梅
脑筋急转弯
情景导入
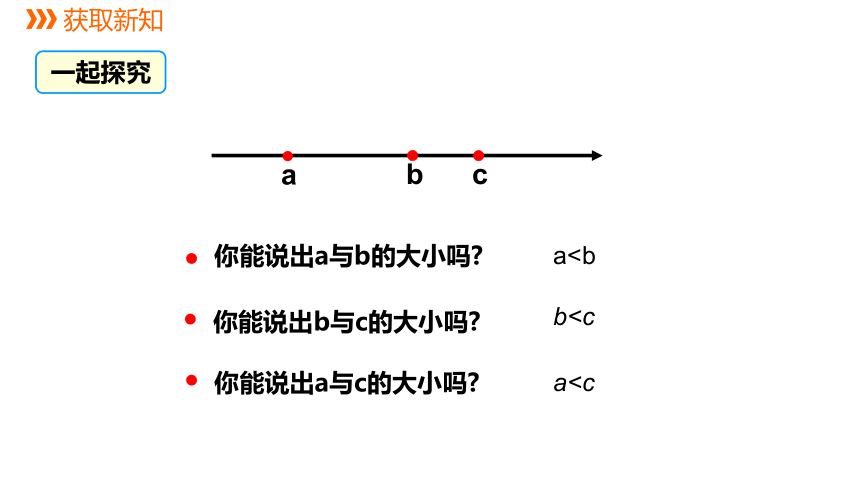
aba你能说出a与b的大小吗
你能说出b与c的大小吗
你能说出a与c的大小吗
a
b
c
获取新知
一起探究
若a<b,b<c,
则a<c.
这个性质也叫做不等式的传递性.
归 纳
不等式的基本性质1
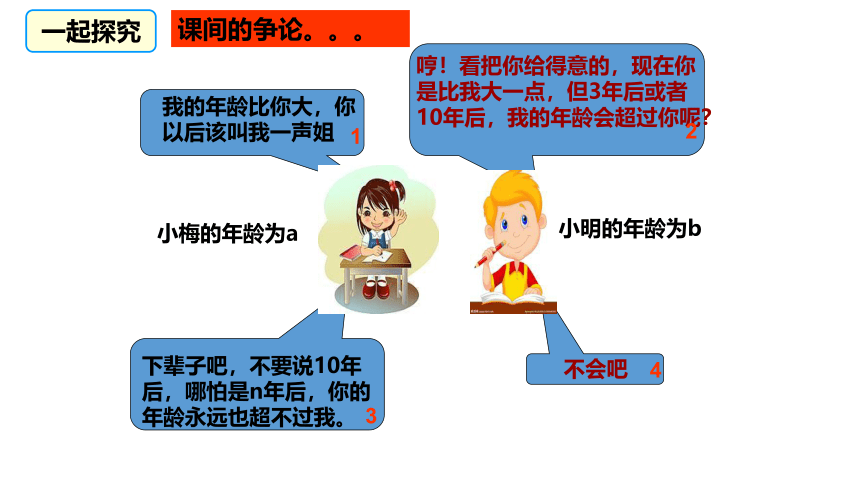
我的年龄比你大,你以后该叫我一声姐
哼!看把你给得意的,现在你是比我大一点,但3年后或者10年后,我的年龄会超过你呢?
1
2
下辈子吧,不要说10年后,哪怕是n年后,你的年龄永远也超不过我。
3
不会吧
4
小梅的年龄为a
小明的年龄为b
课间的争论。。。
一起探究
如果小梅现在的年龄为a岁,小明的年龄为b岁,则a b
那么c年以后,则a+c b+c
c年以前,则a-c b-c
>
>
>
b
a
b+c
a+c
c
c
b-c
a-c
b
a
c
c
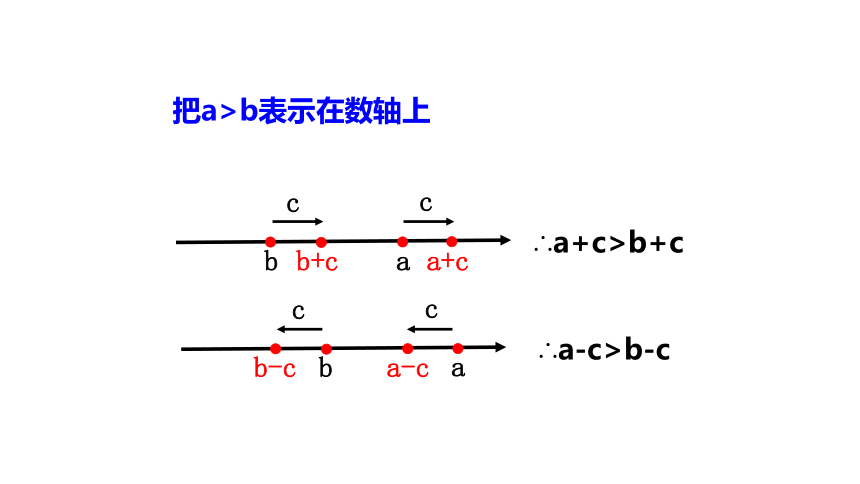
把a>b表示在数轴上
∴a+c>b+c
∴a-c>b-c
不等式的两边都加上(或减去)
同一个数,所得到的不等式仍成立.
即 如果a>b,那么a+c>b+c,a-c>b-c;
如果a<b,那么a+c<b+c,a-c<b-c.
不等式的基本性质2
归 纳
不等号方向不变
你有什么发现吗?
8__12
8×4__12×4
8÷3__12÷3
<
(–4)__(– 6)
(– 4)×(–2)__(– 6)×(–2)
(– 4)÷(–4)__(– 6)÷(–4)
<
<
<
比较大小
一起探究
不等式的两边都乘以(或除以)同一个正数, 所得的不等式仍成立;
不等式的两边都乘以(或除以)同一个负数,必须把不等号的方向改变,所得的不等式成立;
<
<
1、不等式的两边都乘以(或除以)同一个正数,所得的不等式仍成立;(正数不变向)
2、不等式的两边都乘以(或除以)同一个负数,必须把不等号的方向改变,所得的不等式成立. (负数要变向)
不等式的基本性质3
归 纳
口诀记忆法:
加减方向不变
乘除正数方向也不变
乘除负数方向要改变
不等号方向改变
等式与不等式性质的对比
等式的性质 不等式的性质 性质 性质内容 性质 性质内容
传递性 若a=b,b=c,则a=c 传递性 若a性质1 等式两边都加上(或减去)同一个数或同一个整式,所得结果仍是等式. 性质1 不等式的两边都加上(或减去)同一个数,所得到的不等式仍成立。
性质2 等式两边都乘(或除以)同一个0的数,所得结果仍是等式. 性质2 不等式的两边都乘(或除以)同一个正数,所得的不等式仍成立
不等式的两边都乘(或除以)同一个负数,必须改变不等号的方向,所得的不等式成立。
例1 已知a<0 ,试比较2a与a的大小.
你有哪些方法?
例题讲解
特殊值法:
设a=-1,则 2a=-2.
∵-2<-1,
∴2a <a.
作差法:
∵2a-a=a <0,
∴2a<a.
利用不等式基本性质2:
∵a<0,
∴ a+a<0+a,
即2a <a.
利用不等式的基本性质3:
∵2>1,a<0,
∴2a<a.
如图,在数轴上分别表示2a和a的点(a<0).
2a位于a的左边,所以2a<a.
0
a
2a
∣a∣
∣a∣
数形结合:
x>-1
不等式的基本性质2
x>-3
不等式的基本性质3
不等式的基本性质3
(1)若x+1>0,两边同加上-1,
得_________ (依据: ________________ );
(2)若2x>-6,两边同除以2,
得_________ (依据:________________ );
(3)若 x≤ ,两边同乘 -3,
得 ________ (依据:_____________________).
例2 填空:
x≥
例3 选择适当的不等号填空,并说明理由.
>
>
(6)若a>0,且(1-b)a<0,则b _1
>
不等式的基本性质
课堂小结
性质1:若a<b,b<c,则a<c。
性质2:不等式的两边都加上(或减去)同一个数,所得到的不等式仍成立.
性质3:
不等式的两边都乘(或都除以)同一个正数,所得到的不等式仍成立;
不等式的两边都乘(或都除以)同一个负数,必须把不等号的方向改变,所得到的不等式成立.
(传递性)
(不等号方向不变)
(不等号方向不变)
(不等号方向改变)
1.选择适当的不等号,并说明理由
已知a>b,则a+1 b+1
已知a>b,则2a 2b
已知a>b,则-3a -3b
已知a>b,则-3a+2 -3b+2
已知a>b,则4a-3 4b-3
随堂演练
2.选择适当的不等号填空:
(1)若a<b,b<2a-1,则a______2a-1
(4)若a ≥b,则2-a_____2-b
(3)若-a<b,则a_____-b
(2)若a>-b,则a+b______0
>
>
≥
<
3.若 xay,则 a 满足的条件是( )
A.a≥0 B.a≤0
C.a>0 D.a<0
D
4.若a>b,且(x+2)a<(x+2)b,则x的取值范围为 .
x<-2
解∶ 2x一8<2y一8.
理由∶∵x不等式的两边都乘以2,得2x<2y,不等式的两边都减8,得 2x-8<2y-8.
5.已知x6.在一家超市中,商品甲的价格比商品乙的价格高,但又不到商品乙价格的两倍.临近新年,商家决定把商品价格都提高10%.问:提价后商品甲的价格仍比商品乙的价格高,但不到商品乙价格的两倍吗?如果每件商品各涨5元呢?
解:设甲、乙两件商品的价格分别为x元、y元.
根据题意,得x>y,x<2y.
涨价10%后,甲、乙两件商品的价格分别为1.1x元、1.1y元,
根据不等式的基本性质3,得1.1x>1.1y,1.1x<2.2y=2×1.1y,
即提价后商品甲的价格仍比商品乙的价格高,但不到商品乙价格的两倍.涨价5元后,甲、乙两件商品的价格分别为(x+5)元、(y+5)元,
由不等式的基本性质2,
可得x+5>y+5,x+5<2y+5,
而2y+5<2(y+5),
即x+5<2(y+5),
即涨价5元后商品甲的价格仍比商品乙的价格高,但不到商品乙价格的两倍.
第三章 一元一次不等式
3.2 不等式的基本性质
【思考】
判断下列说法是否正确:
1.若a=b,b=c,则 a=c
2.若a=b,则 a+1=b+1
3.若a=b,则 3a=3b
等式的基本性质
知识回顾
两对父子却只有3个人。为什么?
嗯?。。。。
儿子说:“我今年a岁了”
爸爸说:“我今年b岁了”
爷爷说:“我今年c岁了”
请问a与c的大小关系?
小明
小梅
脑筋急转弯
情景导入
a
你能说出b与c的大小吗
你能说出a与c的大小吗
a
b
c
获取新知
一起探究
若a<b,b<c,
则a<c.
这个性质也叫做不等式的传递性.
归 纳
不等式的基本性质1
我的年龄比你大,你以后该叫我一声姐
哼!看把你给得意的,现在你是比我大一点,但3年后或者10年后,我的年龄会超过你呢?
1
2
下辈子吧,不要说10年后,哪怕是n年后,你的年龄永远也超不过我。
3
不会吧
4
小梅的年龄为a
小明的年龄为b
课间的争论。。。
一起探究
如果小梅现在的年龄为a岁,小明的年龄为b岁,则a b
那么c年以后,则a+c b+c
c年以前,则a-c b-c
>
>
>
b
a
b+c
a+c
c
c
b-c
a-c
b
a
c
c
把a>b表示在数轴上
∴a+c>b+c
∴a-c>b-c
不等式的两边都加上(或减去)
同一个数,所得到的不等式仍成立.
即 如果a>b,那么a+c>b+c,a-c>b-c;
如果a<b,那么a+c<b+c,a-c<b-c.
不等式的基本性质2
归 纳
不等号方向不变
你有什么发现吗?
8__12
8×4__12×4
8÷3__12÷3
<
(–4)__(– 6)
(– 4)×(–2)__(– 6)×(–2)
(– 4)÷(–4)__(– 6)÷(–4)
<
<
<
比较大小
一起探究
不等式的两边都乘以(或除以)同一个正数, 所得的不等式仍成立;
不等式的两边都乘以(或除以)同一个负数,必须把不等号的方向改变,所得的不等式成立;
<
<
1、不等式的两边都乘以(或除以)同一个正数,所得的不等式仍成立;(正数不变向)
2、不等式的两边都乘以(或除以)同一个负数,必须把不等号的方向改变,所得的不等式成立. (负数要变向)
不等式的基本性质3
归 纳
口诀记忆法:
加减方向不变
乘除正数方向也不变
乘除负数方向要改变
不等号方向改变
等式与不等式性质的对比
等式的性质 不等式的性质 性质 性质内容 性质 性质内容
传递性 若a=b,b=c,则a=c 传递性 若a
性质2 等式两边都乘(或除以)同一个0的数,所得结果仍是等式. 性质2 不等式的两边都乘(或除以)同一个正数,所得的不等式仍成立
不等式的两边都乘(或除以)同一个负数,必须改变不等号的方向,所得的不等式成立。
例1 已知a<0 ,试比较2a与a的大小.
你有哪些方法?
例题讲解
特殊值法:
设a=-1,则 2a=-2.
∵-2<-1,
∴2a <a.
作差法:
∵2a-a=a <0,
∴2a<a.
利用不等式基本性质2:
∵a<0,
∴ a+a<0+a,
即2a <a.
利用不等式的基本性质3:
∵2>1,a<0,
∴2a<a.
如图,在数轴上分别表示2a和a的点(a<0).
2a位于a的左边,所以2a<a.
0
a
2a
∣a∣
∣a∣
数形结合:
x>-1
不等式的基本性质2
x>-3
不等式的基本性质3
不等式的基本性质3
(1)若x+1>0,两边同加上-1,
得_________ (依据: ________________ );
(2)若2x>-6,两边同除以2,
得_________ (依据:________________ );
(3)若 x≤ ,两边同乘 -3,
得 ________ (依据:_____________________).
例2 填空:
x≥
例3 选择适当的不等号填空,并说明理由.
>
>
(6)若a>0,且(1-b)a<0,则b _1
>
不等式的基本性质
课堂小结
性质1:若a<b,b<c,则a<c。
性质2:不等式的两边都加上(或减去)同一个数,所得到的不等式仍成立.
性质3:
不等式的两边都乘(或都除以)同一个正数,所得到的不等式仍成立;
不等式的两边都乘(或都除以)同一个负数,必须把不等号的方向改变,所得到的不等式成立.
(传递性)
(不等号方向不变)
(不等号方向不变)
(不等号方向改变)
1.选择适当的不等号,并说明理由
已知a>b,则a+1 b+1
已知a>b,则2a 2b
已知a>b,则-3a -3b
已知a>b,则-3a+2 -3b+2
已知a>b,则4a-3 4b-3
随堂演练
2.选择适当的不等号填空:
(1)若a<b,b<2a-1,则a______2a-1
(4)若a ≥b,则2-a_____2-b
(3)若-a<b,则a_____-b
(2)若a>-b,则a+b______0
>
>
≥
<
3.若 x
A.a≥0 B.a≤0
C.a>0 D.a<0
D
4.若a>b,且(x+2)a<(x+2)b,则x的取值范围为 .
x<-2
解∶ 2x一8<2y一8.
理由∶∵x
5.已知x
解:设甲、乙两件商品的价格分别为x元、y元.
根据题意,得x>y,x<2y.
涨价10%后,甲、乙两件商品的价格分别为1.1x元、1.1y元,
根据不等式的基本性质3,得1.1x>1.1y,1.1x<2.2y=2×1.1y,
即提价后商品甲的价格仍比商品乙的价格高,但不到商品乙价格的两倍.涨价5元后,甲、乙两件商品的价格分别为(x+5)元、(y+5)元,
由不等式的基本性质2,
可得x+5>y+5,x+5<2y+5,
而2y+5<2(y+5),
即x+5<2(y+5),
即涨价5元后商品甲的价格仍比商品乙的价格高,但不到商品乙价格的两倍.
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
