浙教版数学八年级上册 4.2 第2课时建立适当的直角坐标系 同步课件(共16张PPT)
文档属性
| 名称 | 浙教版数学八年级上册 4.2 第2课时建立适当的直角坐标系 同步课件(共16张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 457.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-08 00:00:00 | ||
图片预览


文档简介
(共16张PPT)
第四章 图形与坐标
4.2 第2课时 建立适当的直角坐标系
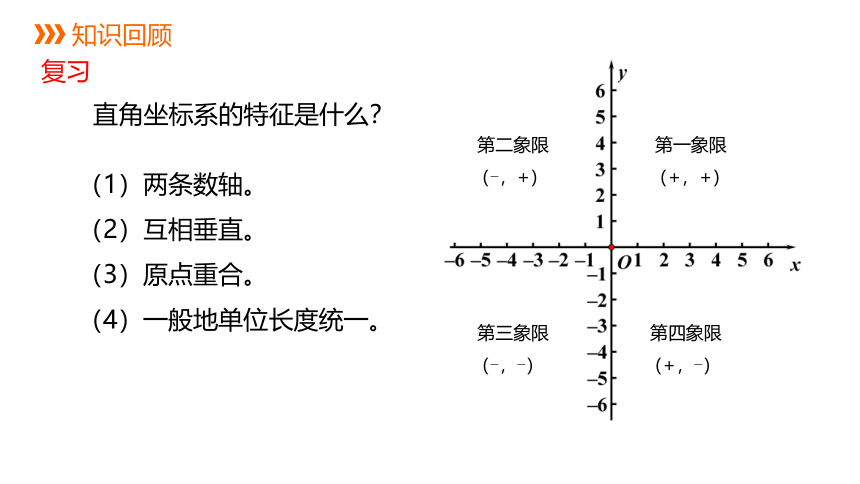
直角坐标系的特征是什么?
(1)两条数轴。
(2)互相垂直。
(3)原点重合。
(4)一般地单位长度统一。
第一象限
(+,+)
第二象限
(-,+)
第三象限
(-,-)
第四象限
(+,-)
知识回顾
复习
1
-1
1
2
3
-3
x
-2
y
4
2
5
3
6
O
A
C
D
B
1
-1
1
2
3
-3
x
-2
y
4
2
5
3
6
O
1
-1
1
2
3
-3
x
-2
y
4
2
5
3
6
O
1
-1
1
2
3
-3
x
-2
y
4
2
5
3
6
O
1
-1
1
2
3
-3
x
-2
y
4
2
5
3
6
O
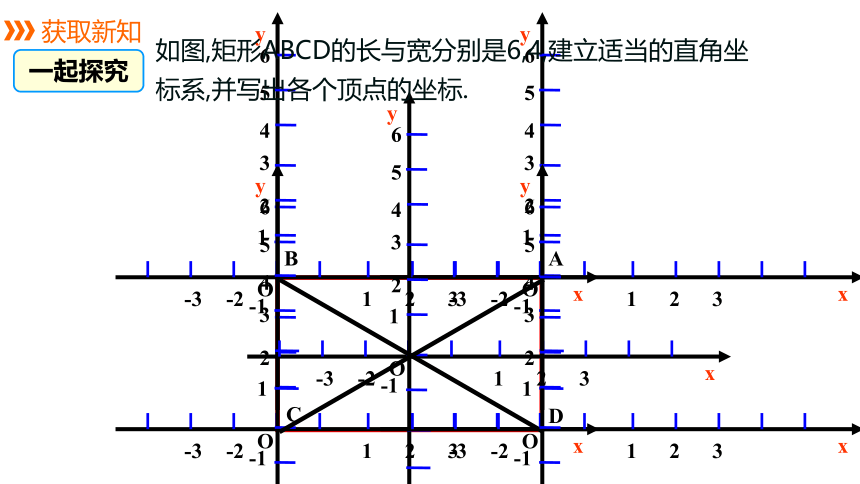
如图,矩形ABCD的长与宽分别是6,4,建立适当的直角坐标系,并写出各个顶点的坐标.
获取新知
一起探究
要确定某点的位置在于, 建立适当的直角坐标系。
1.选择适当的点作为原点;(充分利用特殊点)
2.适当的直线作为坐标轴(充分利用特殊边)
3.选择适当的距离为单位长度。
(一般按比例选择)
归 纳
x
y
A
B
C
D
-1
-2
-1
-2
1
2
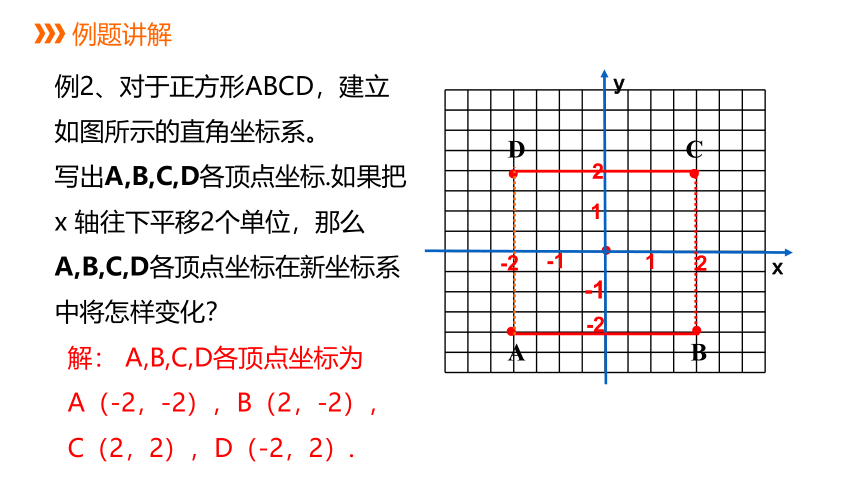
例2、对于正方形ABCD,建立如图所示的直角坐标系。
写出A,B,C,D各顶点坐标.如果把 x 轴往下平移2个单位,那么A,B,C,D各顶点坐标在新坐标系中将怎样变化?
解: A,B,C,D各顶点坐标为
A(-2,-2),B(2,-2),
C(2,2),D(-2,2).
1
2
例题讲解
x
y
A
B
C
D
-1
-2
1
4
3
2
1
2
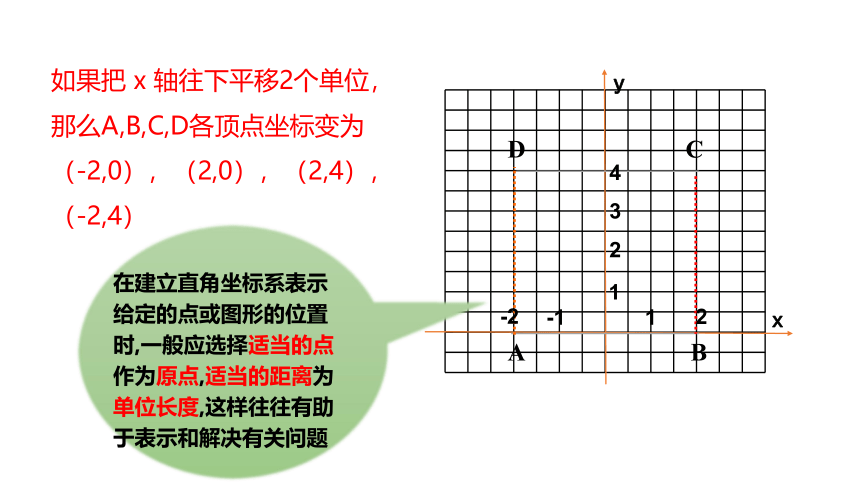
如果把 x 轴往下平移2个单位,那么A,B,C,D各顶点坐标变为
(-2,0),(2,0),(2,4),(-2,4)
在建立直角坐标系表示给定的点或图形的位置时,一般应选择适当的点作为原点,适当的距离为单位长度,这样往往有助于表示和解决有关问题
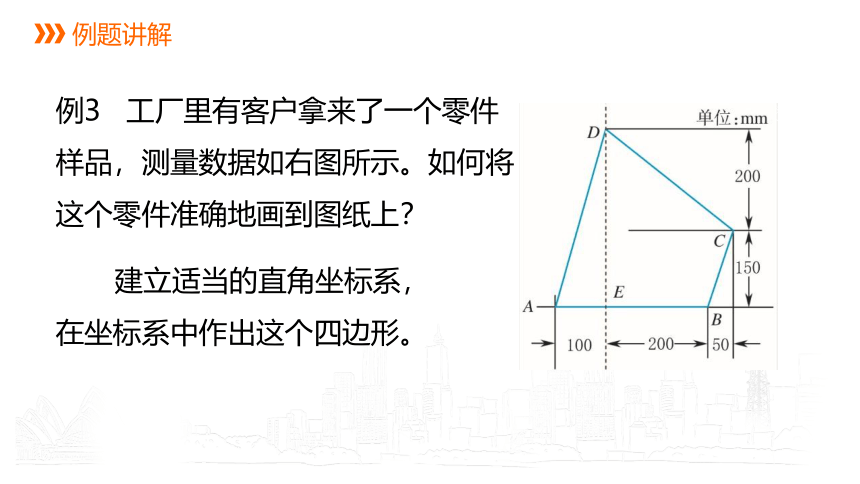
例3 工厂里有客户拿来了一个零件样品,测量数据如右图所示。如何将这个零件准确地画到图纸上?
建立适当的直角坐标系,
在坐标系中作出这个四边形。
例题讲解
(1)为了较方便地确定点A,点B在坐标系中的坐标,可怎样选择x轴?为较方便地确定点D的坐标,如何选择y轴?
(2)根据所标注的尺寸,零件较大怎么办?
思 考
解:建立直角坐标系如右图,选择比例为1:10,取点E为直角坐标系的原点,使线段AB在X轴上,则可得A、B、C、D各点的坐标分别为
y(cm)
x(cm)
O
A(-1,0)
B(2,0)
C(2.5,1.5)
D(0,3.5)
如图四边形ABCD就是所求作的图形
1
3
2
-1
1
2
3
方法一
解:建立直角坐标系如右图,选择比例为1:10,取点E为直角坐标系的原点,使线段AB在X轴上,则可得A、B、C、D各点的坐标分别为
y(cm)
x(cm)
O
A(0,0)
B(3,0)
C(3.5,1.5)
D(1,3.5)
如图四边形ABCD就是所求作的图形
方法二
假山
1.图为某公园门口看到的平面示意图,你能用坐标表示出它们的地理位置吗 若按图建立坐标系,则各景点的坐标分别为多少
喷泉
马戏城
游戏车
九曲桥
-4 -3 -2 -1 O 1 2 3 4
-2
-1
5
4
3
2
1
x
y
-3
(3,3)
(4,-1)
(0,-3)
(-3,-2)
(-3,4)
确定单位长度.
随堂演练
2.长方形零件如图(单位:mm),建立适当的坐标系,用坐标表示孔中心的位置.
15
35
解:如图建立平面直角坐标系,则孔中心的位置是(15,35).
x
y
o
3.这是某乡镇的示意图.试建立直角坐标系,用坐标表示各地的位置:
(1,3)
(3,3)
(-1,1)
(-3,-1)
(2,-2)
(-3,-4)
(3,-3)
O
1
1
x
y
4.已知某镇的镇政府、镇中心小学、农技站的位置如图,假设用线段连结这三个地点,恰好形成一个正三角形,且边长为2km,试选取适当的比例,建立直角坐标系,并在坐标平面内画出这三个地点的位置,并标出坐标。
镇政府
镇中心小学
农机站
1
2
3
-3
x
-2
-2
-3
o
-1
y
4
2
5
3
6
1
镇政府
农技站
镇中心小学
1
2
3
-3
x
-2
-2
-3
o
-1
y
4
2
5
3
6
1
1
2
3
-3
x
-2
-2
-3
o
-1
y
4
2
5
3
6
1
建立适当的直角坐标系
课堂小结
1.建立坐标系,选择一个适当的参照点为原点、确定x轴、 y轴的正方向;
2.根据具体问题确定适当的比例尺,在坐标轴上标出单位长度;
3.在坐标平面内画出这些点、写出各点的坐标和各个地点的名称.
第四章 图形与坐标
4.2 第2课时 建立适当的直角坐标系
直角坐标系的特征是什么?
(1)两条数轴。
(2)互相垂直。
(3)原点重合。
(4)一般地单位长度统一。
第一象限
(+,+)
第二象限
(-,+)
第三象限
(-,-)
第四象限
(+,-)
知识回顾
复习
1
-1
1
2
3
-3
x
-2
y
4
2
5
3
6
O
A
C
D
B
1
-1
1
2
3
-3
x
-2
y
4
2
5
3
6
O
1
-1
1
2
3
-3
x
-2
y
4
2
5
3
6
O
1
-1
1
2
3
-3
x
-2
y
4
2
5
3
6
O
1
-1
1
2
3
-3
x
-2
y
4
2
5
3
6
O
如图,矩形ABCD的长与宽分别是6,4,建立适当的直角坐标系,并写出各个顶点的坐标.
获取新知
一起探究
要确定某点的位置在于, 建立适当的直角坐标系。
1.选择适当的点作为原点;(充分利用特殊点)
2.适当的直线作为坐标轴(充分利用特殊边)
3.选择适当的距离为单位长度。
(一般按比例选择)
归 纳
x
y
A
B
C
D
-1
-2
-1
-2
1
2
例2、对于正方形ABCD,建立如图所示的直角坐标系。
写出A,B,C,D各顶点坐标.如果把 x 轴往下平移2个单位,那么A,B,C,D各顶点坐标在新坐标系中将怎样变化?
解: A,B,C,D各顶点坐标为
A(-2,-2),B(2,-2),
C(2,2),D(-2,2).
1
2
例题讲解
x
y
A
B
C
D
-1
-2
1
4
3
2
1
2
如果把 x 轴往下平移2个单位,那么A,B,C,D各顶点坐标变为
(-2,0),(2,0),(2,4),(-2,4)
在建立直角坐标系表示给定的点或图形的位置时,一般应选择适当的点作为原点,适当的距离为单位长度,这样往往有助于表示和解决有关问题
例3 工厂里有客户拿来了一个零件样品,测量数据如右图所示。如何将这个零件准确地画到图纸上?
建立适当的直角坐标系,
在坐标系中作出这个四边形。
例题讲解
(1)为了较方便地确定点A,点B在坐标系中的坐标,可怎样选择x轴?为较方便地确定点D的坐标,如何选择y轴?
(2)根据所标注的尺寸,零件较大怎么办?
思 考
解:建立直角坐标系如右图,选择比例为1:10,取点E为直角坐标系的原点,使线段AB在X轴上,则可得A、B、C、D各点的坐标分别为
y(cm)
x(cm)
O
A(-1,0)
B(2,0)
C(2.5,1.5)
D(0,3.5)
如图四边形ABCD就是所求作的图形
1
3
2
-1
1
2
3
方法一
解:建立直角坐标系如右图,选择比例为1:10,取点E为直角坐标系的原点,使线段AB在X轴上,则可得A、B、C、D各点的坐标分别为
y(cm)
x(cm)
O
A(0,0)
B(3,0)
C(3.5,1.5)
D(1,3.5)
如图四边形ABCD就是所求作的图形
方法二
假山
1.图为某公园门口看到的平面示意图,你能用坐标表示出它们的地理位置吗 若按图建立坐标系,则各景点的坐标分别为多少
喷泉
马戏城
游戏车
九曲桥
-4 -3 -2 -1 O 1 2 3 4
-2
-1
5
4
3
2
1
x
y
-3
(3,3)
(4,-1)
(0,-3)
(-3,-2)
(-3,4)
确定单位长度.
随堂演练
2.长方形零件如图(单位:mm),建立适当的坐标系,用坐标表示孔中心的位置.
15
35
解:如图建立平面直角坐标系,则孔中心的位置是(15,35).
x
y
o
3.这是某乡镇的示意图.试建立直角坐标系,用坐标表示各地的位置:
(1,3)
(3,3)
(-1,1)
(-3,-1)
(2,-2)
(-3,-4)
(3,-3)
O
1
1
x
y
4.已知某镇的镇政府、镇中心小学、农技站的位置如图,假设用线段连结这三个地点,恰好形成一个正三角形,且边长为2km,试选取适当的比例,建立直角坐标系,并在坐标平面内画出这三个地点的位置,并标出坐标。
镇政府
镇中心小学
农机站
1
2
3
-3
x
-2
-2
-3
o
-1
y
4
2
5
3
6
1
镇政府
农技站
镇中心小学
1
2
3
-3
x
-2
-2
-3
o
-1
y
4
2
5
3
6
1
1
2
3
-3
x
-2
-2
-3
o
-1
y
4
2
5
3
6
1
建立适当的直角坐标系
课堂小结
1.建立坐标系,选择一个适当的参照点为原点、确定x轴、 y轴的正方向;
2.根据具体问题确定适当的比例尺,在坐标轴上标出单位长度;
3.在坐标平面内画出这些点、写出各点的坐标和各个地点的名称.
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
