浙教版数学八年级上册 4.3 第2课时 坐标平面内图形的平移 同步课件(共21张PPT)
文档属性
| 名称 | 浙教版数学八年级上册 4.3 第2课时 坐标平面内图形的平移 同步课件(共21张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 337.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-08 19:45:01 | ||
图片预览



文档简介
(共21张PPT)
第四章 图形与平移
4.3 第2课时 坐标平面内图形的平移
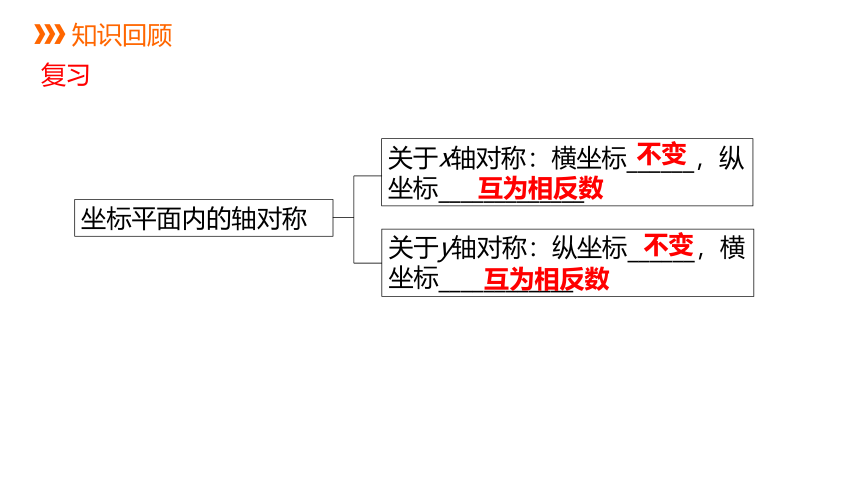
坐标平面内的轴对称
关于x轴对称:横坐标______,纵坐标_____________
不变
互为相反数
关于y轴对称:纵坐标______,横坐标____________
不变
互为相反数
知识回顾
复习
影响平移的因素:
平移的性质:
平移的方向和平移的距离.
平移前后,两个图形的对应点的连线平行(或在同一条直线上)且相等.
平移不改变图形的形状和大小.
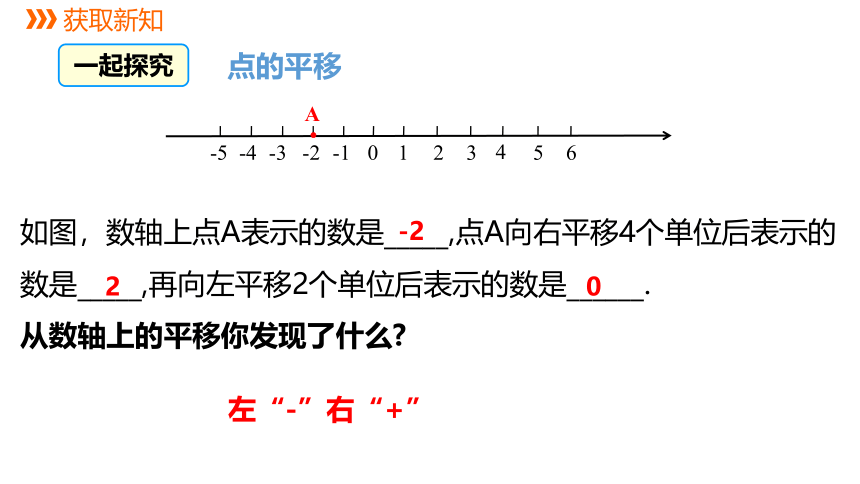
如图,数轴上点A表示的数是_____,点A向右平移4个单位后表示的数是_____,再向左平移2个单位后表示的数是______.
从数轴上的平移你发现了什么
1
-2
-1
0
2
3
4
5
6
-5
-4
-3
A
-2
2
0
左“-”右“+”
获取新知
一起探究
点的平移
A
1
3
5
2
4
6
-1
-2
-3
-4
-5
-6
O
3
4
2
-1
5
-2
-3
-4
-6
-5
6
1
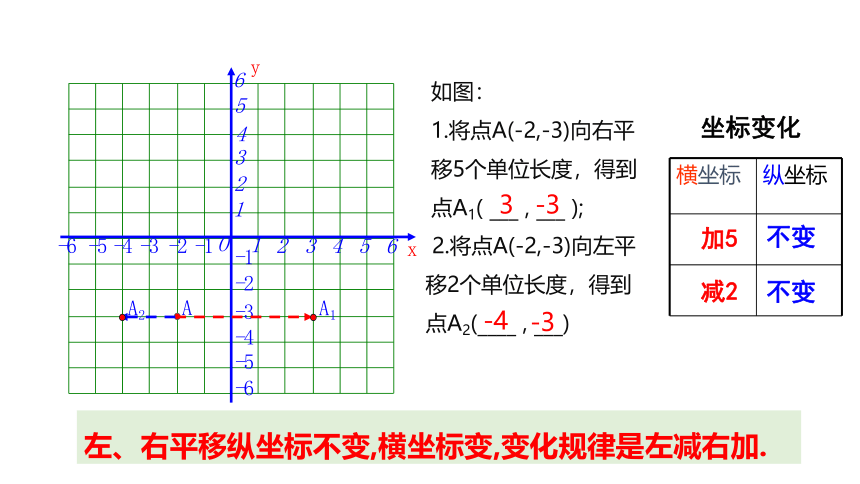
如图:
1.将点A(-2,-3)向右平移5个单位长度,得到点A1( ___ , ___ );
2.将点A(-2,-3)向左平移2个单位长度,得到点A2(____ , ___)
A1
-4
-3
3
-3
A2
y
x
左、右平移纵坐标不变,横坐标变,变化规律是左减右加.
横坐标 纵坐标
坐标变化
加5
减2
不变
不变
A
1
3
5
2
4
6
-1
-2
-3
-4
-5
-6
3
4
2
-1
5
-2
-3
-4
-6
-5
6
0
1
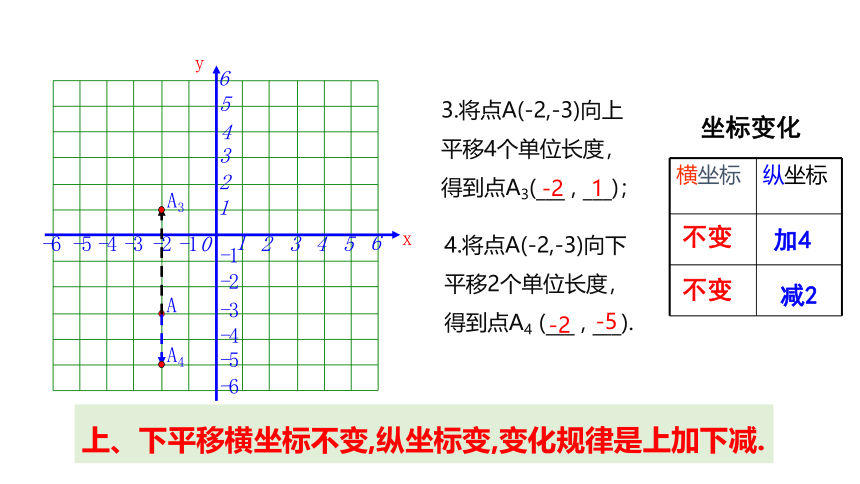
3.将点A(-2,-3)向上平移4个单位长度,得到点A3(___ , ___);
4.将点A(-2,-3)向下平移2个单位长度,得到点A4 (___ , ___).
A3
A4
-2
1
-2
-5
y
x
上、下平移横坐标不变,纵坐标变,变化规律是上加下减.
横坐标 纵坐标
坐标变化
不变
不变
加4
减2
(1)左右平移:
向右平移a个单位
(2)上下平移:
点(x,y) ,
向左平移a个单位
点(x,y) ,
(x+a,y)
(x-a,y)
向上平移b个单位
点(x,y) ,
向下平移b个单位
点(x,y) ,
(x,y+b)
(x,y-b)
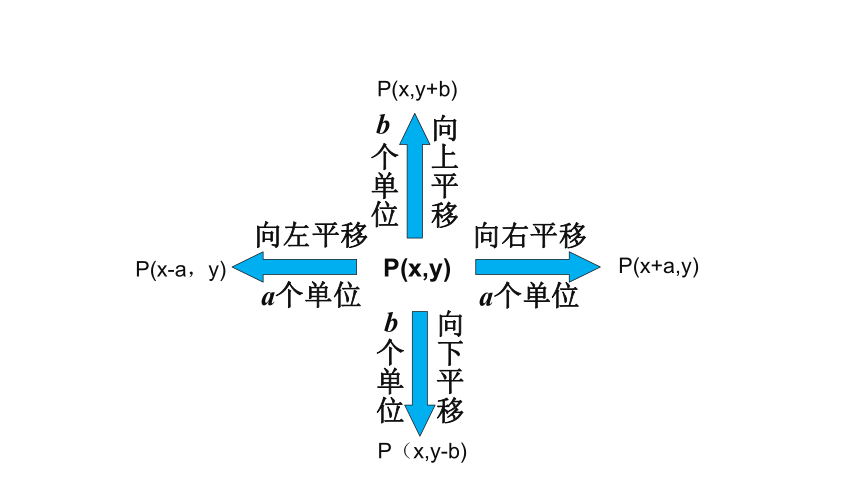
归纳:点的平移
点(x,y) ,
向右平移a个单位, 向下平移b个单位
(x+a,y-b)
向上平移
个单位
b
向下平移
个单位
b
向右平移
a个单位
向左平移
a个单位
P(x,y)
P(x-a,y)
P(x+a,y)
P(x,y+b)
P(x,y-b)
A
1
2
3
0
1
2
4
3
5
-1
-1
-2
B
y
x
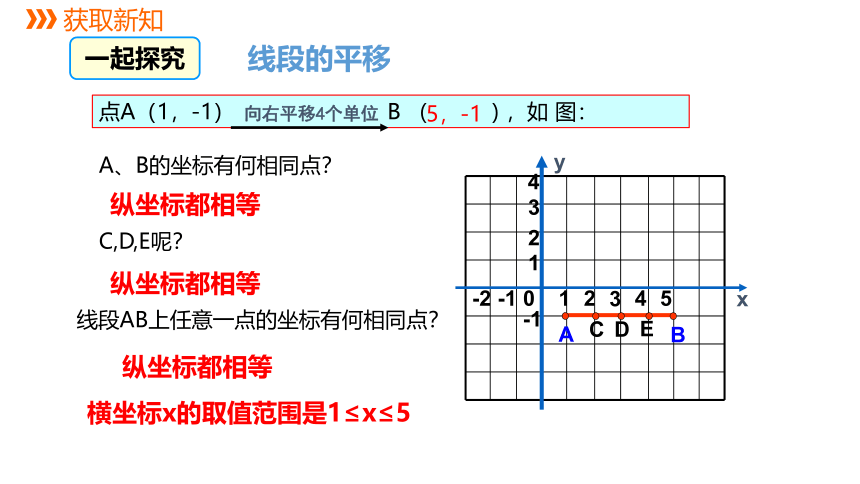
A、B的坐标有何相同点?
线段AB上任意一点的坐标有何相同点?
C
D
E
C,D,E呢?
点A(1,-1) B ( ) ,如 图:
向右平移4个单位
4
5,-1
获取新知
线段的平移
一起探究
纵坐标都相等
纵坐标都相等
纵坐标都相等
横坐标x的取值范围是1≤x≤5
例1 如图,在直角坐标系中,平行于x轴的线段AB上所有点的纵坐标都是-1,横坐标x的取值范围是1≤x ≤5 ,则线段AB上任意一点的坐标可以用“(x,-1) (1≤x ≤5)”表示,按照这样的规定,回答下面的问题:
1、怎样表示线段CD上任意一点的坐标?
A
1
2
3
4
0
1
2
4
3
5
-1
-1
-2
B
C
D
(2, y)(-1≤y ≤3)
例题讲解
2、把线段AB向上平移2.5个单位,作出所得线段A′B′,线段A′B′上任意一点的坐标怎示?
(x, 1.5)(1≤x ≤5)
A
1
2
3
4
0
1
2
4
3
5
-1
-1
-2
B
C
D
A'
B'
C'
D'
3、把线段CD向左平移3个单位,作出所得线段C′D′,线段C′D′上任意一点的坐标怎示?
(-1, y)(-1≤y ≤3)
线段的平移变换即为线段上对应点的平移变换。
A
2
0
2
4
-2
B
例2 (1) 分别求出A,A'的坐标;B,B'的坐标,比较A与A',B与B'之间的坐标变化。
A'
B'
-4
-6
-8
-4
-2
4
6
(2) 从图形甲到图形乙可以看作经过怎样的图形变换?
A(-8,-1)
A'(-3,4)
B(-3,-1)
B' (2,4)
先向右平移5个单位,
再向上平移5个单位
可以看作只经过一次平移变换吗?.
甲
乙
x
y
由A到A′,横坐标增加5,纵坐标增加5;由B到B′,横坐标增加5,纵坐标增加5.
A
2
0
2
4
-2
B
A'
B'
-4
-6
-8
-4
-2
4
6
(2) 从图形甲到图形乙可以看作经过怎样的图形变换?
先向右平移5个单位
再向上平移5个单位
x
y
沿AA'方向平移 个单位
50
1.点P(0,0)先向右平移1个单位,再向下平移2个单位得到点S,
则点S的坐标为( )
A.(1,2) B.(1,-2) C.(-1,2) D.(-1,-2)
2.已知线段MN平行于y轴,且MN的长度为3,若已知点M(2,-2),
则点N的坐标是 .
(2,1)或(2,-5)
B
随堂演练
3.将点A(3,2)向上平移2个单位长度,得到A1,则A1的坐标 为______.
将点A(3,2)向下平移3个单位长度,得到A2,则A2的坐标为______.
将点A(3,2)向左平移4个单位长度,得到A3,则A3的坐标为______.
(3,4)
4.点A1(6,3)是由点A(-2,3)经过 得到的,点B(4,3)向 得到B1(6,3).
向右平移8个单位长度
右平移2个单位长度
(3,-1)
(-1,2)
5.将点A(3,2)向上平移2个单位长度,向左平移4个单位长度得到A1,则A1的坐标 为______.
(-1,4)
6.(1)已知线段 MN=4,MN∥y轴,若点M坐标为(-1,2),则N点坐标为____________________;
(2)已知线段 MN=4,MN∥x轴,若点M坐标为(-1,2),则N点坐标为___________________.
(-1,-2)或(-1,6)
(3,2)或(-5,2)
A
B
C
-4
-5
1
2
3
4
1
2
3
4
-1
-2
-3
-1
-2
-3
o
x
y
(-3,2)
(-2,-1)
(3,0)
7.如图,三角形ABC上任意一点P(x0,y0)经平移后得到的对应点为P1(x0+2,y0+4),将三角形ABC作同样的平移得到三角形A1B1C1.
求A1、B1、C1的坐标.
P(x0,y0)
P1(x0+2,y0+4)
B
解:A(-3,2)经平移后得到(3+2,2+4),即A1(-1,6);
B(-2,-1)经平移后得到
(-2+2,-1+4),即B1(0,3);
C(3,0)经平移后得到(3+2,0+4),即C1(5,4).
C
O
A1
C1
B1
8.在平面直角坐标系中,将坐标为(5,6),(1,2),(3,2),(3,0),(7,0),(7,2),(9,2),(5,6)的点用线段依次连结起来形成一个图案.
(1)纵坐标保持不变,横坐标分别减去3, 所得图案与原图案相比有什么变化?
(2)横坐标保持不变,纵坐标分别乘-1, 所得图案与原图案相比有什么变化?
(3)横坐标加上2,纵坐标减去3, 所得图案与原图案相比有什么变化?
解:如图所示.
(1)纵坐标保持不变,横坐标减去3,所得图案是由原图案向左平移3个单位得到的.
(2)横坐标保持不变,纵坐标分别乘-1,所得图案与原图案关于x轴对称.
(3)横坐标加上2,纵坐标减去3,所得图案是由原图案向右平移2个单位,再向下平移3个单位得到的.
坐标平面内的平移
左右平移
左减右加
上下平移
上加下减
课堂小结
第四章 图形与平移
4.3 第2课时 坐标平面内图形的平移
坐标平面内的轴对称
关于x轴对称:横坐标______,纵坐标_____________
不变
互为相反数
关于y轴对称:纵坐标______,横坐标____________
不变
互为相反数
知识回顾
复习
影响平移的因素:
平移的性质:
平移的方向和平移的距离.
平移前后,两个图形的对应点的连线平行(或在同一条直线上)且相等.
平移不改变图形的形状和大小.
如图,数轴上点A表示的数是_____,点A向右平移4个单位后表示的数是_____,再向左平移2个单位后表示的数是______.
从数轴上的平移你发现了什么
1
-2
-1
0
2
3
4
5
6
-5
-4
-3
A
-2
2
0
左“-”右“+”
获取新知
一起探究
点的平移
A
1
3
5
2
4
6
-1
-2
-3
-4
-5
-6
O
3
4
2
-1
5
-2
-3
-4
-6
-5
6
1
如图:
1.将点A(-2,-3)向右平移5个单位长度,得到点A1( ___ , ___ );
2.将点A(-2,-3)向左平移2个单位长度,得到点A2(____ , ___)
A1
-4
-3
3
-3
A2
y
x
左、右平移纵坐标不变,横坐标变,变化规律是左减右加.
横坐标 纵坐标
坐标变化
加5
减2
不变
不变
A
1
3
5
2
4
6
-1
-2
-3
-4
-5
-6
3
4
2
-1
5
-2
-3
-4
-6
-5
6
0
1
3.将点A(-2,-3)向上平移4个单位长度,得到点A3(___ , ___);
4.将点A(-2,-3)向下平移2个单位长度,得到点A4 (___ , ___).
A3
A4
-2
1
-2
-5
y
x
上、下平移横坐标不变,纵坐标变,变化规律是上加下减.
横坐标 纵坐标
坐标变化
不变
不变
加4
减2
(1)左右平移:
向右平移a个单位
(2)上下平移:
点(x,y) ,
向左平移a个单位
点(x,y) ,
(x+a,y)
(x-a,y)
向上平移b个单位
点(x,y) ,
向下平移b个单位
点(x,y) ,
(x,y+b)
(x,y-b)
归纳:点的平移
点(x,y) ,
向右平移a个单位, 向下平移b个单位
(x+a,y-b)
向上平移
个单位
b
向下平移
个单位
b
向右平移
a个单位
向左平移
a个单位
P(x,y)
P(x-a,y)
P(x+a,y)
P(x,y+b)
P(x,y-b)
A
1
2
3
0
1
2
4
3
5
-1
-1
-2
B
y
x
A、B的坐标有何相同点?
线段AB上任意一点的坐标有何相同点?
C
D
E
C,D,E呢?
点A(1,-1) B ( ) ,如 图:
向右平移4个单位
4
5,-1
获取新知
线段的平移
一起探究
纵坐标都相等
纵坐标都相等
纵坐标都相等
横坐标x的取值范围是1≤x≤5
例1 如图,在直角坐标系中,平行于x轴的线段AB上所有点的纵坐标都是-1,横坐标x的取值范围是1≤x ≤5 ,则线段AB上任意一点的坐标可以用“(x,-1) (1≤x ≤5)”表示,按照这样的规定,回答下面的问题:
1、怎样表示线段CD上任意一点的坐标?
A
1
2
3
4
0
1
2
4
3
5
-1
-1
-2
B
C
D
(2, y)(-1≤y ≤3)
例题讲解
2、把线段AB向上平移2.5个单位,作出所得线段A′B′,线段A′B′上任意一点的坐标怎示?
(x, 1.5)(1≤x ≤5)
A
1
2
3
4
0
1
2
4
3
5
-1
-1
-2
B
C
D
A'
B'
C'
D'
3、把线段CD向左平移3个单位,作出所得线段C′D′,线段C′D′上任意一点的坐标怎示?
(-1, y)(-1≤y ≤3)
线段的平移变换即为线段上对应点的平移变换。
A
2
0
2
4
-2
B
例2 (1) 分别求出A,A'的坐标;B,B'的坐标,比较A与A',B与B'之间的坐标变化。
A'
B'
-4
-6
-8
-4
-2
4
6
(2) 从图形甲到图形乙可以看作经过怎样的图形变换?
A(-8,-1)
A'(-3,4)
B(-3,-1)
B' (2,4)
先向右平移5个单位,
再向上平移5个单位
可以看作只经过一次平移变换吗?.
甲
乙
x
y
由A到A′,横坐标增加5,纵坐标增加5;由B到B′,横坐标增加5,纵坐标增加5.
A
2
0
2
4
-2
B
A'
B'
-4
-6
-8
-4
-2
4
6
(2) 从图形甲到图形乙可以看作经过怎样的图形变换?
先向右平移5个单位
再向上平移5个单位
x
y
沿AA'方向平移 个单位
50
1.点P(0,0)先向右平移1个单位,再向下平移2个单位得到点S,
则点S的坐标为( )
A.(1,2) B.(1,-2) C.(-1,2) D.(-1,-2)
2.已知线段MN平行于y轴,且MN的长度为3,若已知点M(2,-2),
则点N的坐标是 .
(2,1)或(2,-5)
B
随堂演练
3.将点A(3,2)向上平移2个单位长度,得到A1,则A1的坐标 为______.
将点A(3,2)向下平移3个单位长度,得到A2,则A2的坐标为______.
将点A(3,2)向左平移4个单位长度,得到A3,则A3的坐标为______.
(3,4)
4.点A1(6,3)是由点A(-2,3)经过 得到的,点B(4,3)向 得到B1(6,3).
向右平移8个单位长度
右平移2个单位长度
(3,-1)
(-1,2)
5.将点A(3,2)向上平移2个单位长度,向左平移4个单位长度得到A1,则A1的坐标 为______.
(-1,4)
6.(1)已知线段 MN=4,MN∥y轴,若点M坐标为(-1,2),则N点坐标为____________________;
(2)已知线段 MN=4,MN∥x轴,若点M坐标为(-1,2),则N点坐标为___________________.
(-1,-2)或(-1,6)
(3,2)或(-5,2)
A
B
C
-4
-5
1
2
3
4
1
2
3
4
-1
-2
-3
-1
-2
-3
o
x
y
(-3,2)
(-2,-1)
(3,0)
7.如图,三角形ABC上任意一点P(x0,y0)经平移后得到的对应点为P1(x0+2,y0+4),将三角形ABC作同样的平移得到三角形A1B1C1.
求A1、B1、C1的坐标.
P(x0,y0)
P1(x0+2,y0+4)
B
解:A(-3,2)经平移后得到(3+2,2+4),即A1(-1,6);
B(-2,-1)经平移后得到
(-2+2,-1+4),即B1(0,3);
C(3,0)经平移后得到(3+2,0+4),即C1(5,4).
C
O
A1
C1
B1
8.在平面直角坐标系中,将坐标为(5,6),(1,2),(3,2),(3,0),(7,0),(7,2),(9,2),(5,6)的点用线段依次连结起来形成一个图案.
(1)纵坐标保持不变,横坐标分别减去3, 所得图案与原图案相比有什么变化?
(2)横坐标保持不变,纵坐标分别乘-1, 所得图案与原图案相比有什么变化?
(3)横坐标加上2,纵坐标减去3, 所得图案与原图案相比有什么变化?
解:如图所示.
(1)纵坐标保持不变,横坐标减去3,所得图案是由原图案向左平移3个单位得到的.
(2)横坐标保持不变,纵坐标分别乘-1,所得图案与原图案关于x轴对称.
(3)横坐标加上2,纵坐标减去3,所得图案是由原图案向右平移2个单位,再向下平移3个单位得到的.
坐标平面内的平移
左右平移
左减右加
上下平移
上加下减
课堂小结
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
