浙教版数学八年级上册 5.3 第2课时 待定系数法求一次函数表达式 同步课件(共22张PPT)
文档属性
| 名称 | 浙教版数学八年级上册 5.3 第2课时 待定系数法求一次函数表达式 同步课件(共22张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 238.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-08 00:00:00 | ||
图片预览








文档简介
(共22张PPT)
第五章 一次函数
5.3 第2课时 待定系数法求一次函数表达式
正比例函数的解析式是什么?
一次函数的解析式是什么?
y=kx
(k为常数,且k≠0)
y=kx+b
(k、b为常数,且k≠0)
当b=0时,
一次函数y=kx+b就变形为正比例函数y=kx
问题一:
知识回顾
复习
形如y=kx+b(k不为零)的函数, 称y是x的一次函数
形如y=kx (k不为零)的函数, 称y是x的正比例函数
y=kx+b
y=kx
b=0
分别写出下列一次函数的一次项系数k和常数项b的值
(1) s = - t +4
(2) y=-2(x-1)+x
问题二
已知y是x的正比例函数,且当x=2时y=- 6.求y与x之间的关系式;
这道题是根据自变量与函数的一对对应值求出正比例函数解析式.
也就是题目已知了 中的 b=0.
那如果不限定这个条件,我们该如何求一次函数解析式呢?
情景导入
(2) 若x=1,y=5,则函数关系式 _______.
问题1 正比例函数y=kx(k≠0)
y= 5x
问题2 若y与x成正比例,且当x=0.5时,y=3
则y与x的关系式为_______
y=6x
(1) 若比例系数为 - , 则函数关系式为 ;
1
3
y= x
1
3
-
获取新知
一起探究
问题3 已知y是x的正比例函数,当x=5时,y=4,
求此函数解析式以及比例系数.
如何确定正比例函数的解析式
设y=kx
待确定
解k
代
回代
一对x,y值代入.
待定系数法
问题4 已知y是x的一次函数,当x=3时, y=1;
当x= -2时, y= -14 。
求这个一次函数的解析式
如何确定一次函数的解析式
两对x,y值代入
待确定
待确定
解k、b
代
设 y=kx+b
回代
待定系数法
用待定系数法求函数解析式的一般步骤?
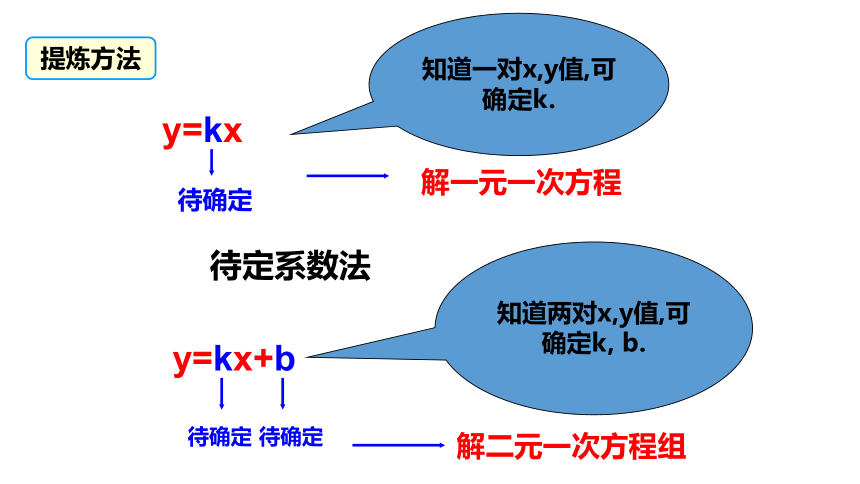
y=kx
y=kx+b
知道一对x,y值,可确定k.
知道两对x,y值,可确定k, b.
待确定
待确定
待确定
解一元一次方程
解二元一次方程组
待定系数法
提炼方法
例1 已知 y 是 x 的一次函数当x=3时, y=1;当x=-2时,y=-14.求这个一次函数的表达式.
解 设一次函数的表达式为y=kx+b (k≠0).
将 x=3,y=1和x=-2,y=-14分别代入 y=kx+b,得
∴所求一次函数的表达式为 y=3x-8.
例题讲解
设
代
解
写
待定系数法
一般地,已知一次函数的自变量与函数的两对对应值,可以按以下步骤求这个一次函数的解析式:
1.设所求的一次函数解析式为 ,其中k、b为待定的常数.
2.把两对已知的自变量与函数的对应值分别代入 ,得到关于k、b的二元一次方程组.
3.解这个关于k、b的二元一次方程组,求出k、b的值.
4.把求得的k、b的值代入 ,就写出所求的一次函数.
获取新知
例2 某地区从1995年底开始,沙漠面积几乎每年以相同的速度增长.据有关报道,到2001年底,该地区的沙漠面积已从1998年底的100.6万公顷扩展到101.2万公顷。
①沙漠面积是怎么变化的?
②沙漠面积变化跟什么有关系?
③设95年年底沙漠面积为b万公顷,每经过一年,沙漠面积增加k万公顷.经过x年,沙漠面积增加到y万公顷.则y 和 x的关系?
y=kx+b
④也就是说可选用一次函数来描述沙漠面积的变化,只要
求出系数k和b.
⑤根据题设条件能否建立关于这两个常数的二元一次方程组
(1)可选用什么数学方法来描述该地区的沙漠面积的变化
(2)如果该地区的沙漠化得不到治理,那么到2020年底,该地区的沙漠面积将增加到多少公顷
98年年底沙漠面积100.6万公顷;
01年年底沙漠面积101.2万公顷
例题讲解
例2 某地区从1995年底开始,沙漠面积几乎每年以相同的速度增长.据有关
报道,到2001年底,该地区的沙漠面积已从1998年底的100.6万公顷扩展到101.2万公顷。
(1)可选用什么数学方法来描述该地区的沙漠面积的变化
(2)如果该地区的沙漠化得不到治理,那么到2020年底,该地区的沙漠面积将增加到多少公顷
解 (1)设从1995年底该地区的沙漠面积为b万公顷,沙漠面积的增长速度为k万公顷/年,经过x年沙漠的面积增加到y万公顷.由题意,得
∵当x=3时,y=100.6;当x=6时,y=101.2
∴把它们分别代入y=kx + b,得
y=k x + b,
解这个方程组,得
这样该地区沙漠面积的变化就由
一次函数 y=0.2 x+100来进行描述。
(2) 把 x = 25 代入 y=0.2x+100,
得 y=0.2 ╳25+100=105(万公顷)。
可见,如果该地区的沙漠化得不到治理,按相同的增长速度,那么2020年底,该地区的沙漠面积将增加到105万公顷。
1.已知一次函数y=x+b,当x=5时,y=4,求b的值.
解:将x=5,y=4代入一次函数解析式中得:4=×5+b,即2+b=4,
解得:b=2.
21cnjy.com
随堂演练
2.已知 y 是 x 的一次函数当x=3时, y=1;当x=-2时,y=-4.求这个一次函数的表达式.
解 设一次函数的表达式为y=kx+b(k≠0).
将 x=3,y=1和x=-2,y=-4分别代入 y=kx+b,得
∴所求一次函数的表达式为y=x-2.
3. 已知一次函数的图象经过点(9,0)和点(24,20),写出函数解析式.
解:设一次函数解析式为y=kx+b,
因为函数图象过点 (9,0)和(24,20),
所以得:
函数解析式为y= x-12
0=9k+b,
20=24k+b,
解得:
k=
b=-12
4.已知y+m与x-n成正比例(其中m,n是常数)
(1)y是x的一次函数吗?
(2)如果当y=-15时,x=11;当x=7时,y=1;求y关于x的函数解析式
解:(1)
设y+m=k(x-n),
(k是常数,且 k≠0)
∴y=kx-kn-m
∵k、m、n都是常数
∴ -kn-m 是常数
∴ y是关于x的一次函数
整体
(2)设y=kx+b, 则
11k+b= -15
7k+b=1
{
∴y=- 4x+29
k =-4
b =29
{
解得
答: y关于x的函数解析式为
y=-4x+29
∴ y+m=kx-kn
5.已知:在某个一次函数中,当自变量x=2时,对应的函数值是1;当自变量x=-4时,对应的函数值是10.求当自变量x=2022时,该函数对应的函数值是多少?
解:设这个一次函数是y=kx+b,
x=2 x=-4
把 y=1 y=10 分别代入,
得 2k+b=1
-4k+b=10,
解得 k=-
b=4 所以,y=-x+4,
所以,当x=2022时,y=-×2022+4=-3029.
6.某商店购进一批单价为16元的日用品,销售一段时间后,为了获得更多利润,商店决定提高销售价格.经试验发现,若按每件20元的价格销售时,每月能卖360件;若按每件25元的价格销售时,每月能卖210件.假定每月销售件数y(件)是价格x(元/件)的一次函数.
(1)试求y与x之间的关系式;
(2)在商品不积压,且不考虑其它因素的条件下,问销售价格定为多少时,才能使每月获得最大利润?每月的最大利润是多少(总利润=总收入-总成本)?
解:(1)依题意设y=kx+b,则有
360=20k+b
210=25k+b
解得k=-30,b=960
∴y=-30x+960(16≤x≤32)
(2)每月获得利润P=(-30x+960)(x-16)
=30(-x+32)(x-16)
=30(-x2+48x-512)
=-30(x-24)2+1920
∴在16≤x≤32范围内,当x=24时,P有最大值,最大值为1920.
答:当价格为24元时,才能使每月获得最大利润,最大利润为1920元.
21cnjy.com
②当k<0时,函数值随x增大而减小,
∴当x=-2时,y=9,x=6时,y=-11,
-2k+b=9
6k+b=-11
∴解得 k=-
b=4
∴函数解析式为y=-x+4.
因此,函数解析式为y=x-6或y=-x+4.
待定系数法
设
列
写
解
课堂小结
所求的一次函数解析式为y=kx+b;
依已知列出关于k、b的方程组
解方程组,求得k、b;
把k、b的值代入y=kx+b ,写出一次函数解析式
第五章 一次函数
5.3 第2课时 待定系数法求一次函数表达式
正比例函数的解析式是什么?
一次函数的解析式是什么?
y=kx
(k为常数,且k≠0)
y=kx+b
(k、b为常数,且k≠0)
当b=0时,
一次函数y=kx+b就变形为正比例函数y=kx
问题一:
知识回顾
复习
形如y=kx+b(k不为零)的函数, 称y是x的一次函数
形如y=kx (k不为零)的函数, 称y是x的正比例函数
y=kx+b
y=kx
b=0
分别写出下列一次函数的一次项系数k和常数项b的值
(1) s = - t +4
(2) y=-2(x-1)+x
问题二
已知y是x的正比例函数,且当x=2时y=- 6.求y与x之间的关系式;
这道题是根据自变量与函数的一对对应值求出正比例函数解析式.
也就是题目已知了 中的 b=0.
那如果不限定这个条件,我们该如何求一次函数解析式呢?
情景导入
(2) 若x=1,y=5,则函数关系式 _______.
问题1 正比例函数y=kx(k≠0)
y= 5x
问题2 若y与x成正比例,且当x=0.5时,y=3
则y与x的关系式为_______
y=6x
(1) 若比例系数为 - , 则函数关系式为 ;
1
3
y= x
1
3
-
获取新知
一起探究
问题3 已知y是x的正比例函数,当x=5时,y=4,
求此函数解析式以及比例系数.
如何确定正比例函数的解析式
设y=kx
待确定
解k
代
回代
一对x,y值代入.
待定系数法
问题4 已知y是x的一次函数,当x=3时, y=1;
当x= -2时, y= -14 。
求这个一次函数的解析式
如何确定一次函数的解析式
两对x,y值代入
待确定
待确定
解k、b
代
设 y=kx+b
回代
待定系数法
用待定系数法求函数解析式的一般步骤?
y=kx
y=kx+b
知道一对x,y值,可确定k.
知道两对x,y值,可确定k, b.
待确定
待确定
待确定
解一元一次方程
解二元一次方程组
待定系数法
提炼方法
例1 已知 y 是 x 的一次函数当x=3时, y=1;当x=-2时,y=-14.求这个一次函数的表达式.
解 设一次函数的表达式为y=kx+b (k≠0).
将 x=3,y=1和x=-2,y=-14分别代入 y=kx+b,得
∴所求一次函数的表达式为 y=3x-8.
例题讲解
设
代
解
写
待定系数法
一般地,已知一次函数的自变量与函数的两对对应值,可以按以下步骤求这个一次函数的解析式:
1.设所求的一次函数解析式为 ,其中k、b为待定的常数.
2.把两对已知的自变量与函数的对应值分别代入 ,得到关于k、b的二元一次方程组.
3.解这个关于k、b的二元一次方程组,求出k、b的值.
4.把求得的k、b的值代入 ,就写出所求的一次函数.
获取新知
例2 某地区从1995年底开始,沙漠面积几乎每年以相同的速度增长.据有关报道,到2001年底,该地区的沙漠面积已从1998年底的100.6万公顷扩展到101.2万公顷。
①沙漠面积是怎么变化的?
②沙漠面积变化跟什么有关系?
③设95年年底沙漠面积为b万公顷,每经过一年,沙漠面积增加k万公顷.经过x年,沙漠面积增加到y万公顷.则y 和 x的关系?
y=kx+b
④也就是说可选用一次函数来描述沙漠面积的变化,只要
求出系数k和b.
⑤根据题设条件能否建立关于这两个常数的二元一次方程组
(1)可选用什么数学方法来描述该地区的沙漠面积的变化
(2)如果该地区的沙漠化得不到治理,那么到2020年底,该地区的沙漠面积将增加到多少公顷
98年年底沙漠面积100.6万公顷;
01年年底沙漠面积101.2万公顷
例题讲解
例2 某地区从1995年底开始,沙漠面积几乎每年以相同的速度增长.据有关
报道,到2001年底,该地区的沙漠面积已从1998年底的100.6万公顷扩展到101.2万公顷。
(1)可选用什么数学方法来描述该地区的沙漠面积的变化
(2)如果该地区的沙漠化得不到治理,那么到2020年底,该地区的沙漠面积将增加到多少公顷
解 (1)设从1995年底该地区的沙漠面积为b万公顷,沙漠面积的增长速度为k万公顷/年,经过x年沙漠的面积增加到y万公顷.由题意,得
∵当x=3时,y=100.6;当x=6时,y=101.2
∴把它们分别代入y=kx + b,得
y=k x + b,
解这个方程组,得
这样该地区沙漠面积的变化就由
一次函数 y=0.2 x+100来进行描述。
(2) 把 x = 25 代入 y=0.2x+100,
得 y=0.2 ╳25+100=105(万公顷)。
可见,如果该地区的沙漠化得不到治理,按相同的增长速度,那么2020年底,该地区的沙漠面积将增加到105万公顷。
1.已知一次函数y=x+b,当x=5时,y=4,求b的值.
解:将x=5,y=4代入一次函数解析式中得:4=×5+b,即2+b=4,
解得:b=2.
21cnjy.com
随堂演练
2.已知 y 是 x 的一次函数当x=3时, y=1;当x=-2时,y=-4.求这个一次函数的表达式.
解 设一次函数的表达式为y=kx+b(k≠0).
将 x=3,y=1和x=-2,y=-4分别代入 y=kx+b,得
∴所求一次函数的表达式为y=x-2.
3. 已知一次函数的图象经过点(9,0)和点(24,20),写出函数解析式.
解:设一次函数解析式为y=kx+b,
因为函数图象过点 (9,0)和(24,20),
所以得:
函数解析式为y= x-12
0=9k+b,
20=24k+b,
解得:
k=
b=-12
4.已知y+m与x-n成正比例(其中m,n是常数)
(1)y是x的一次函数吗?
(2)如果当y=-15时,x=11;当x=7时,y=1;求y关于x的函数解析式
解:(1)
设y+m=k(x-n),
(k是常数,且 k≠0)
∴y=kx-kn-m
∵k、m、n都是常数
∴ -kn-m 是常数
∴ y是关于x的一次函数
整体
(2)设y=kx+b, 则
11k+b= -15
7k+b=1
{
∴y=- 4x+29
k =-4
b =29
{
解得
答: y关于x的函数解析式为
y=-4x+29
∴ y+m=kx-kn
5.已知:在某个一次函数中,当自变量x=2时,对应的函数值是1;当自变量x=-4时,对应的函数值是10.求当自变量x=2022时,该函数对应的函数值是多少?
解:设这个一次函数是y=kx+b,
x=2 x=-4
把 y=1 y=10 分别代入,
得 2k+b=1
-4k+b=10,
解得 k=-
b=4 所以,y=-x+4,
所以,当x=2022时,y=-×2022+4=-3029.
6.某商店购进一批单价为16元的日用品,销售一段时间后,为了获得更多利润,商店决定提高销售价格.经试验发现,若按每件20元的价格销售时,每月能卖360件;若按每件25元的价格销售时,每月能卖210件.假定每月销售件数y(件)是价格x(元/件)的一次函数.
(1)试求y与x之间的关系式;
(2)在商品不积压,且不考虑其它因素的条件下,问销售价格定为多少时,才能使每月获得最大利润?每月的最大利润是多少(总利润=总收入-总成本)?
解:(1)依题意设y=kx+b,则有
360=20k+b
210=25k+b
解得k=-30,b=960
∴y=-30x+960(16≤x≤32)
(2)每月获得利润P=(-30x+960)(x-16)
=30(-x+32)(x-16)
=30(-x2+48x-512)
=-30(x-24)2+1920
∴在16≤x≤32范围内,当x=24时,P有最大值,最大值为1920.
答:当价格为24元时,才能使每月获得最大利润,最大利润为1920元.
21cnjy.com
②当k<0时,函数值随x增大而减小,
∴当x=-2时,y=9,x=6时,y=-11,
-2k+b=9
6k+b=-11
∴解得 k=-
b=4
∴函数解析式为y=-x+4.
因此,函数解析式为y=x-6或y=-x+4.
待定系数法
设
列
写
解
课堂小结
所求的一次函数解析式为y=kx+b;
依已知列出关于k、b的方程组
解方程组,求得k、b;
把k、b的值代入y=kx+b ,写出一次函数解析式
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
