浙教版数学八年级上册 5.3 第1课时 一次函数的概念 同步课件(共20张PPT)
文档属性
| 名称 | 浙教版数学八年级上册 5.3 第1课时 一次函数的概念 同步课件(共20张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 259.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-08 00:00:00 | ||
图片预览








文档简介
(共20张PPT)
第五章 一次函数
5.3 第1课时 一次函数的概念
在某个变化过程中,有两个变量x和y,如果给定一个x值,相应地就确定一个y值,那么我们称y是x的函数,其中x是自变量.
什么叫函数?
知识回顾
复习
1、小明准备将平时的零用钱节约一些储存起来。他已 存有50元,从现在起每月节存15元,那么小明的存款数y(元)与月数x的关系式_____________.
2、为迎合“绿色乡村”的举办理念,小明积极参与改善生态环境的活动。今年植树节,他种了一棵高为1米的树苗. 这种树苗平均每年长高0.2米.那么树高h(米)与年数t之间的函数关系式是________________.
h=0.2t+1
y=15x+50
情景导入
列式
(2)预计每小时可销售150件毛绒玩具,则当天内毛绒玩具剩余量y(件)与销售时间x(小时)之间的关系式为_____________ 。
(1)毛绒玩具销售金额w与销售数量n之间的函数关系式为 ;
3、北京某体育用品商店购进2000件毛绒玩具纪念品,其销售单价为78元.
w=78n
y= 2000-150x
比较下列各函数,它们有哪些共同的特征?
y=15x +50
h=0.2t+1
w=78n
y= -150x+2000
y= -32x
这些函数有什么共同点 不同点
你能用哪一种函数关系式表示它们
获取新知
一起探究
(1)等号两边的代数式都是整式;
(2)自变量的次数是一次;
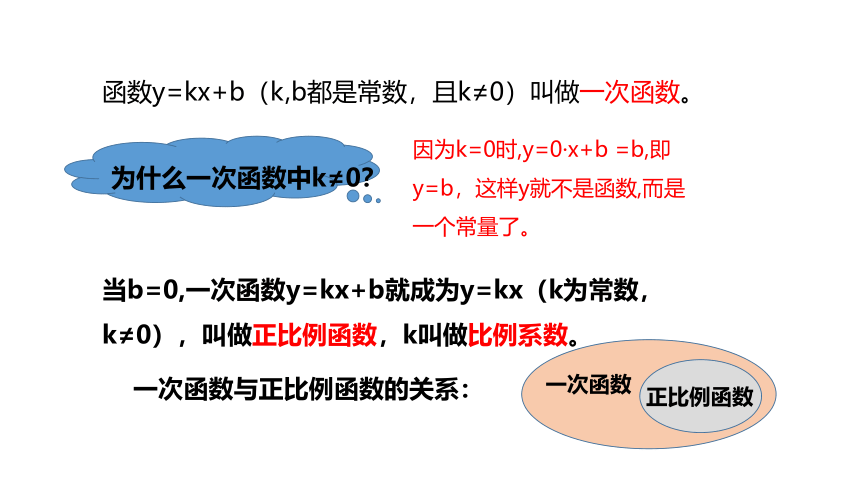
函数y=kx+b(k,b都是常数,且k≠0)叫做一次函数。
当b=0,一次函数y=kx+b就成为y=kx(k为常数,k≠0),叫做正比例函数,k叫做比例系数。
一次函数与正比例函数的关系:
一次函数
正比例函数
为什么一次函数中k≠0?
因为k=0时,y=0·x+b =b,即y=b,这样y就不是函数,而是一个常量了。
C=2πr
y= x+200
t=
y=2(3-x)
s=x(50-x)
不是一次函数,也不是正比例函数函数
一次函数
正比例函数
s=-x2+50x,不是一次函数,也不是正比例函数
下列函数中,哪些是一次函数?哪些是正比例函数?系数k和常数项b的值各是多少?
k=2π,b=0
k=,b=200
k=-2,b=6
一次函数
注:求k值和b值,必须化成一般形式y=kx+b
做一做
例1 已知函数y=(2m-1)x+1-3m,m为何值时.
(1)这个函数是正比例函数;
(2)这个函数为一次函数;
解:(1)∵函数y=(2m-1)x+1-3m是正比例函数,
∴1-3m=0,2m-1≠0,解得:m=;
(2)∵函数y=(2m-1)x+1-3m是一次函数,
∴2m-1≠0,解得:m≠;
例题讲解
例2 求出下列各题中x和y之间的关系式,并判断y是否为x的一次函数,是否为正比例函数。
(1)某农场种植玉米,每平方米种玉米6株,玉米数y与种植面积x(m2)之间的关系;
(2)正方形周长x与面积y之间的关系;
(3)等腰三角形ABC的周长为16cm,底边BC长为ycm,腰AB长为x,求y与x之间的关系。
解:y=6x , y是x的一次函数,也是正比例函数
解:y=() , y不是x的一次函数,也不是正比例函数
解:y=16-2x , y是x的一次函数,但不是x的正比例函数
例3 按国家1999年8月30日公布的有关个人所得税的规定,全月应纳税所得额不超过500元的税率为5%,超过500元至2000元部分的税率为10%。
(1)设全月应纳税所得额为 x元,且 ,应纳个人所得税为 y元,求 y关于 x的函数解析式和自变量的取值范围;
x
3500
5000
8000
3%
10%
0
0
1500
4500
应纳税所得额x
工资
3%
10%
解:(1)y = 1500×3%+(x-1500)×10%
= 0.1x-105
(1500<x≤4500 )
∴ 所求的函数解析式为y= 0.1x-105 (1500<x≤4500 )
(2)小明妈妈的工资为每月2600元,小聪妈妈的工资为每月2800元,问她俩每月应缴个人所得税多少元?
x
3500
5000
8000
3%
10%
0
0
1500
4500
应纳税所得额x
工资
3%
10%
(2)小聪妈妈全月应纳税所得额为5500-3500=2000(元)
将x=2000代入函数表达式,得
y =0.1×2000-105=95(元)
答:小聪妈妈每月应缴个人所得税95元。
1.下列函数(1)y=πx;(2)y=2x-1;(3)y=;(4)y=x2-1中,是一次函数的有( )
A.4个 B.3个 C.2个 D.1个
C
随堂演练
(1) 当m = 时,y是x的正比例函数;
2、已知函数y=(m-3)xm-1;
(2) 若x=-2, y=a 满足(1)中所求的函数关系式,则a= .
3、已知一次函数y=kx+3,当x=2时y=-1,则k= 。
2
2
-2
3.写出下列各题中x与y的关系式,并判断y是否是x的正比例函数?
(1)电报收费标准是每个字0.1元,电报费y(元)与字数x(个)之间的函数关系;
(2)地面气温是28℃,如果每升高1km,气温下降5℃,则气温x(℃)与高度y(km)的关系;
(3)圆面积y(cm2)与半径x(cm)的关系。
解:(1)y=0.1x,y是x的正比例函数;
(2)y=28-5x,y不是x的正比例函数;
(3)y= πx2,y不是x的正比例函数。
21cnjy.com
4.已知y-3与x成正比例,并且x=4时,y=7,求y与x之间的函数关系式.
解:依题意,设y-3与x之间的函数关系式为y-3=kx,
∵x=4时,y=7,∴7-3=4k,解得k=1.
∴y-3=x,即y=x+3.
5.有一块10公顷的成熟麦田,用一台收割速度为0.5公顷每小时的小麦收割机来收割.
(1)求收割的面积y(单位:公顷)与收割时间x(单位:时)之间的函数关系式;
(2)求收割完这块麦田需用的时间.
解:(1)y=0.5x;
(2)把y=10代入y=0.5x中,得10=0.5x.
解得x=20,即收割完这块麦田需要20小时.
6.已知函数y=(m+1)x+(m2-1)当m取什么值时,y是x的一次函数?当m取什么值时,y是x的正比例函数.
解:由函数是一次函数可得,
m+1≠0,解得 m≠-1,
所以,m≠-1时,y是x的一次函数;
函数为正比例函数时,
m+1≠0且m2-1=0,
解得 m=1,
所以,当m=1时,y是x的正比例函数.
7.某市为了鼓励居民节约用电,采用分段计费的方法按月计算每户家庭的电费.月用电量不超过200度时,按0.55元/度计费;月用电量超过200度时,其中的200度仍按0.55元/度计费,超过部分按0.70元/度计费.设每户家庭月用电量为x度时,应交电费y元.
(1)分别求出0≤x≤200和x>200时,y与x的函数表达式;
(2)小明家5月份交纳电费117元,小明家这个月用电多少度?
解:(1)当0≤x≤200时,
y与x的函数表达式是y=0.55x;
当x>200时,
y与x的函数表达式是y=0.55×200+0.7(x﹣200),即y=0.7x﹣30。
(2)∵小明家5月份的电费超过110元,
∴把y=117代入y=0.7x﹣30中,得x=210。
答:小明家5月份用电210度。
一次函数
一次函数的定义
形如函数y=kx+b(k,b都是常数,且k≠0)
正比例函数的定义
课堂小结
当b=0,一次函数y=kx+b就成为y=kx(k为常数,k≠0)
第五章 一次函数
5.3 第1课时 一次函数的概念
在某个变化过程中,有两个变量x和y,如果给定一个x值,相应地就确定一个y值,那么我们称y是x的函数,其中x是自变量.
什么叫函数?
知识回顾
复习
1、小明准备将平时的零用钱节约一些储存起来。他已 存有50元,从现在起每月节存15元,那么小明的存款数y(元)与月数x的关系式_____________.
2、为迎合“绿色乡村”的举办理念,小明积极参与改善生态环境的活动。今年植树节,他种了一棵高为1米的树苗. 这种树苗平均每年长高0.2米.那么树高h(米)与年数t之间的函数关系式是________________.
h=0.2t+1
y=15x+50
情景导入
列式
(2)预计每小时可销售150件毛绒玩具,则当天内毛绒玩具剩余量y(件)与销售时间x(小时)之间的关系式为_____________ 。
(1)毛绒玩具销售金额w与销售数量n之间的函数关系式为 ;
3、北京某体育用品商店购进2000件毛绒玩具纪念品,其销售单价为78元.
w=78n
y= 2000-150x
比较下列各函数,它们有哪些共同的特征?
y=15x +50
h=0.2t+1
w=78n
y= -150x+2000
y= -32x
这些函数有什么共同点 不同点
你能用哪一种函数关系式表示它们
获取新知
一起探究
(1)等号两边的代数式都是整式;
(2)自变量的次数是一次;
函数y=kx+b(k,b都是常数,且k≠0)叫做一次函数。
当b=0,一次函数y=kx+b就成为y=kx(k为常数,k≠0),叫做正比例函数,k叫做比例系数。
一次函数与正比例函数的关系:
一次函数
正比例函数
为什么一次函数中k≠0?
因为k=0时,y=0·x+b =b,即y=b,这样y就不是函数,而是一个常量了。
C=2πr
y= x+200
t=
y=2(3-x)
s=x(50-x)
不是一次函数,也不是正比例函数函数
一次函数
正比例函数
s=-x2+50x,不是一次函数,也不是正比例函数
下列函数中,哪些是一次函数?哪些是正比例函数?系数k和常数项b的值各是多少?
k=2π,b=0
k=,b=200
k=-2,b=6
一次函数
注:求k值和b值,必须化成一般形式y=kx+b
做一做
例1 已知函数y=(2m-1)x+1-3m,m为何值时.
(1)这个函数是正比例函数;
(2)这个函数为一次函数;
解:(1)∵函数y=(2m-1)x+1-3m是正比例函数,
∴1-3m=0,2m-1≠0,解得:m=;
(2)∵函数y=(2m-1)x+1-3m是一次函数,
∴2m-1≠0,解得:m≠;
例题讲解
例2 求出下列各题中x和y之间的关系式,并判断y是否为x的一次函数,是否为正比例函数。
(1)某农场种植玉米,每平方米种玉米6株,玉米数y与种植面积x(m2)之间的关系;
(2)正方形周长x与面积y之间的关系;
(3)等腰三角形ABC的周长为16cm,底边BC长为ycm,腰AB长为x,求y与x之间的关系。
解:y=6x , y是x的一次函数,也是正比例函数
解:y=() , y不是x的一次函数,也不是正比例函数
解:y=16-2x , y是x的一次函数,但不是x的正比例函数
例3 按国家1999年8月30日公布的有关个人所得税的规定,全月应纳税所得额不超过500元的税率为5%,超过500元至2000元部分的税率为10%。
(1)设全月应纳税所得额为 x元,且 ,应纳个人所得税为 y元,求 y关于 x的函数解析式和自变量的取值范围;
x
3500
5000
8000
3%
10%
0
0
1500
4500
应纳税所得额x
工资
3%
10%
解:(1)y = 1500×3%+(x-1500)×10%
= 0.1x-105
(1500<x≤4500 )
∴ 所求的函数解析式为y= 0.1x-105 (1500<x≤4500 )
(2)小明妈妈的工资为每月2600元,小聪妈妈的工资为每月2800元,问她俩每月应缴个人所得税多少元?
x
3500
5000
8000
3%
10%
0
0
1500
4500
应纳税所得额x
工资
3%
10%
(2)小聪妈妈全月应纳税所得额为5500-3500=2000(元)
将x=2000代入函数表达式,得
y =0.1×2000-105=95(元)
答:小聪妈妈每月应缴个人所得税95元。
1.下列函数(1)y=πx;(2)y=2x-1;(3)y=;(4)y=x2-1中,是一次函数的有( )
A.4个 B.3个 C.2个 D.1个
C
随堂演练
(1) 当m = 时,y是x的正比例函数;
2、已知函数y=(m-3)xm-1;
(2) 若x=-2, y=a 满足(1)中所求的函数关系式,则a= .
3、已知一次函数y=kx+3,当x=2时y=-1,则k= 。
2
2
-2
3.写出下列各题中x与y的关系式,并判断y是否是x的正比例函数?
(1)电报收费标准是每个字0.1元,电报费y(元)与字数x(个)之间的函数关系;
(2)地面气温是28℃,如果每升高1km,气温下降5℃,则气温x(℃)与高度y(km)的关系;
(3)圆面积y(cm2)与半径x(cm)的关系。
解:(1)y=0.1x,y是x的正比例函数;
(2)y=28-5x,y不是x的正比例函数;
(3)y= πx2,y不是x的正比例函数。
21cnjy.com
4.已知y-3与x成正比例,并且x=4时,y=7,求y与x之间的函数关系式.
解:依题意,设y-3与x之间的函数关系式为y-3=kx,
∵x=4时,y=7,∴7-3=4k,解得k=1.
∴y-3=x,即y=x+3.
5.有一块10公顷的成熟麦田,用一台收割速度为0.5公顷每小时的小麦收割机来收割.
(1)求收割的面积y(单位:公顷)与收割时间x(单位:时)之间的函数关系式;
(2)求收割完这块麦田需用的时间.
解:(1)y=0.5x;
(2)把y=10代入y=0.5x中,得10=0.5x.
解得x=20,即收割完这块麦田需要20小时.
6.已知函数y=(m+1)x+(m2-1)当m取什么值时,y是x的一次函数?当m取什么值时,y是x的正比例函数.
解:由函数是一次函数可得,
m+1≠0,解得 m≠-1,
所以,m≠-1时,y是x的一次函数;
函数为正比例函数时,
m+1≠0且m2-1=0,
解得 m=1,
所以,当m=1时,y是x的正比例函数.
7.某市为了鼓励居民节约用电,采用分段计费的方法按月计算每户家庭的电费.月用电量不超过200度时,按0.55元/度计费;月用电量超过200度时,其中的200度仍按0.55元/度计费,超过部分按0.70元/度计费.设每户家庭月用电量为x度时,应交电费y元.
(1)分别求出0≤x≤200和x>200时,y与x的函数表达式;
(2)小明家5月份交纳电费117元,小明家这个月用电多少度?
解:(1)当0≤x≤200时,
y与x的函数表达式是y=0.55x;
当x>200时,
y与x的函数表达式是y=0.55×200+0.7(x﹣200),即y=0.7x﹣30。
(2)∵小明家5月份的电费超过110元,
∴把y=117代入y=0.7x﹣30中,得x=210。
答:小明家5月份用电210度。
一次函数
一次函数的定义
形如函数y=kx+b(k,b都是常数,且k≠0)
正比例函数的定义
课堂小结
当b=0,一次函数y=kx+b就成为y=kx(k为常数,k≠0)
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
