九上1.4二次函数应用(中考最新命题方向试题精选)
文档属性
| 名称 | 九上1.4二次函数应用(中考最新命题方向试题精选) |  | |
| 格式 | zip | ||
| 文件大小 | 481.3KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-09 17:00:23 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
二次函数应用专题复习卷
函数类型确定的求二次函数表达式及简单的实际应用
1.已知二次函数y=(m﹣2)x2﹣4x+2m﹣8的图象经过原点,它可以由抛物线y=ax2(a≠0)平移得到,则a的值是 .
2.根据下列条件,求二次函数的解析式
(1)已知二次函数的图象经过点(﹣2,﹣1),且当x=﹣1时,函数有最大值2;
(2)抛物线的对称轴是直线x=1,与x轴的一个交点为(﹣2,0),与y轴交于点(0,12).
已知二次函数y=﹣x2+bx+c的图象过B(﹣1,0),C(2,3)两点.
(1)求此二次函数的表达式.
(2)若此抛物线沿y轴平移一次后过点(﹣2,1),试确定这次平移的方向和距离.
4.在平面直角坐标系中,△AOB的位置如图所示,已知∠AOB=90°,AO=BO,点A的坐标为(﹣3,1).
(1)求点B的坐标;
(2)求过A,O,B三点的抛物线的解析式;
(3)设点B关于抛物线的对称轴l的对称点为B1,求△AB1B的面积.
5.如图,小明的爸爸在相距4m的两树等高位置处拴了一根绳子,做成一个简易的秋千,绳子自然下垂呈抛物线,已知身高1.5m的小明站在距离树1m的地方,头部刚好触到绳子.
(1)求抛物线的函数表达式和自变量的取值范围.
(2)求绳子最低点离地面的距离.
6.如图,一隧道的横截面是由一段抛物线及矩形的三边围成的,隧道宽BC=10米,矩形部分高AB=3米,抛物线型的最高点E离地面OE=6米,按如图建立一个以BC为x轴,OE为y轴的直角坐标系.
(1)求抛物线的解析式;
(2)如果该隧道内设有双车道,现有一辆货运卡车高4.5米,宽3米,这辆货运卡车能顺利通过隧道吗?
7. 如图,在某场足球比赛中,球员甲从球门底部中心点O的正前方10m处起脚射门,足球沿抛物线飞向球门中心线;当足球飞离地面高度为3m时达到最高点,此时足球飞行的水平距离为6m.已知球门的横梁高OA为2.44m.
(1)在如图所示的平面直角坐标系中,问此飞行足球能否进球门?(不计其它情况)
(2)守门员乙站在距离球门2m处,他跳起时手的最大摸高为2.52m,他能阻止球员甲的此次射门吗?如果不能,他至少后退多远才能阻止球员甲的射门?
在一场篮球比赛中,甲球员在距篮4米处跳投,球运行的路线是抛物线,当球运行的水平距离为2.5米时,达到最大高度3.75米,然后球准确落入篮圈.已知篮圈中心到地面的距离为3.05米.
(1)建立如图所示的平面直角坐标系,求抛物线的解析式;
(2)乙球员身高为1.91米,跳起能摸到的高度为3.15米,此时他上前封盖,在离投篮甲球员2米处时起跳,问能否成功封盖住此次投篮?
(3)在(2)条件下若乙球员想要成功封盖甲球员的这次投篮,他离甲球员的距离至多要多少米?
9.小宇和佳佳两人进行羽毛球比赛,小宇发出一颗十分关键的球,出手点为P,P点距离地面的高度为1.5米,羽毛球的运动轨迹是抛物线,并且在距P点水平距离4米处达到最高点,最高点距离地面3.1米,建立如图所示的直角坐标系.
(1)求羽毛球飞行过程中,距地面高度y(米)与飞出的水平距离x(米)之间的函数关系;
(2)已知P点距离小宇对面的场地边线为12米,若佳佳不接球,此球是否会出界?说明理由;
(3)已知球网AB距点O的水平距离是5米,佳佳扣球的最大高度为2米,设佳佳的起跳点C的横坐标为m,若佳佳原地起跳,因佳佳扣球的最大高度(用线段CD表示)低于球的高度而导致扣球失败,求m的取值范围.
10.足球比赛中,某运动员将在地面上的足球对着球门踢出,图中的抛物线是足球的飞行高度y(m)关于飞行时间x(s)的函数图象(不考虑空气的阻力),已知足球飞出1s时,足球的飞行高度是2.44m,足球从飞出到落地共用3s.
(1)求y关于x的函数关系式;
(2)足球的飞行高度能否达到4.88米?请说明理由;
(3)假设没有拦挡,足球将擦着球门左上角射入球门,球门的高为2.44m(如图所示,足球的大小忽略不计).如果为了能及时将足球扑出,那么足球被踢出时,离球门左边框12m处的守门员至少要以多大的平均速度到球门的左边框?
11.某公司推出了一种高效环保型洗涤用品,年初上市后,公司经历了从亏损到盈利的过程,如图的二次函数图象(部分)刻画了该公司年初以来累积利润s(万元)与时间t(月)之间的关系(即前t个月的利润总和s与t之间的关系).根据图象提供的信息,解答下列问题:
(1)求累积利润s(万元)与时间t(月)之间的函数关系式;
(2)求截止到几月末公司累积利润可达30万元;
(3)从第几个月起公司开始盈利?该月公司所获利润是多少万元?
12.如图,有一个横截面边缘为抛物线的隧道入口,隧道入口处的底面宽度为8m,两侧距底面4m高处各有一盏灯,两灯间的水平距离为6m,则这个隧道入口的最大高度为 m(精确到0.1m).
13.如图,一个圆形喷水池的中央竖直安装了一个柱形喷水装置OA,A处的喷头向外喷水,水流在各个方向上沿形状相同的抛物线路径落下,水流喷出的高度y(m)与水平距离x(m)之间的关系式是y=﹣x2+2x+(x>0)
(1)求水流喷出的最大高度是多少m?此时的水平距离是多少m?
(2)若不计其他因素,水池的半径OB至少为多少m,才能使喷出的水流不落在池外?
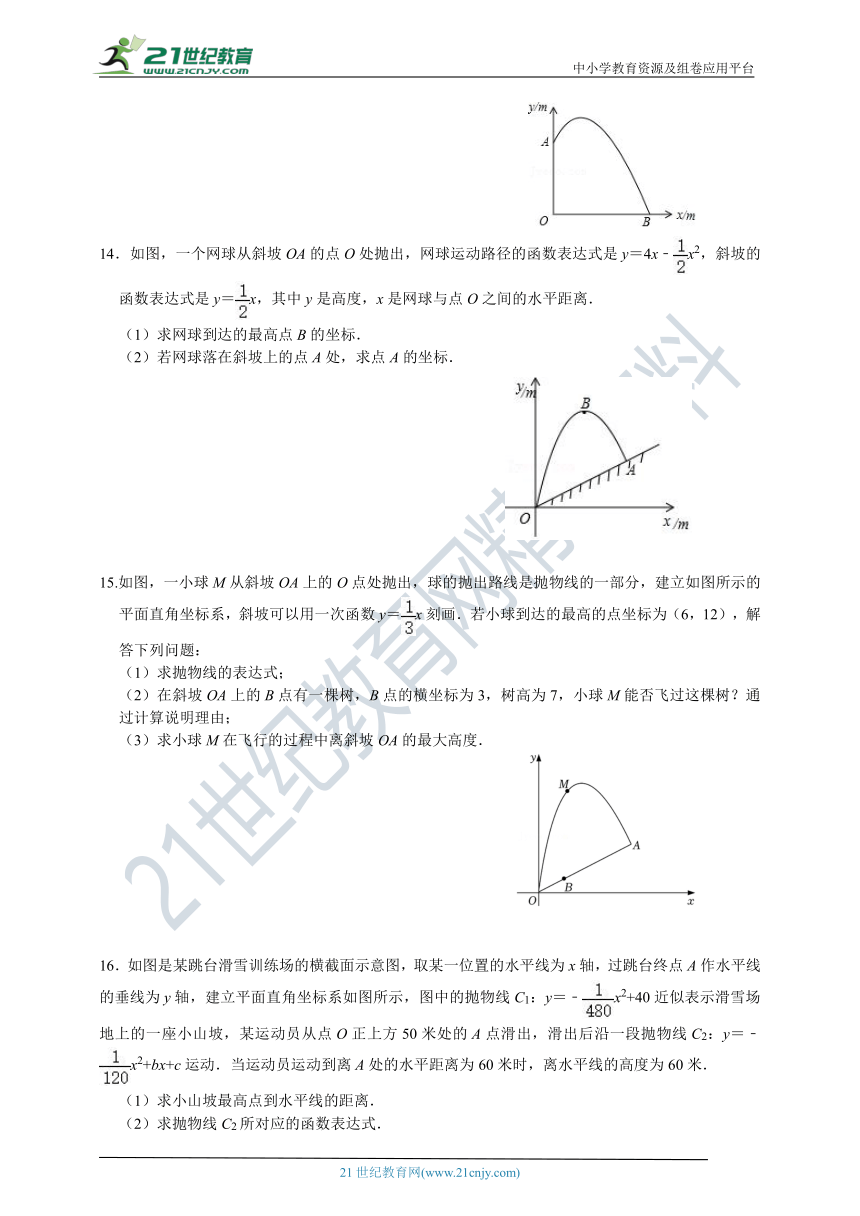
14.如图,一个网球从斜坡OA的点O处抛出,网球运动路径的函数表达式是y=4x﹣x2,斜坡的函数表达式是y=x,其中y是高度,x是网球与点O之间的水平距离.
(1)求网球到达的最高点B的坐标.
(2)若网球落在斜坡上的点A处,求点A的坐标.
15.如图,一小球M从斜坡OA上的O点处抛出,球的抛出路线是抛物线的一部分,建立如图所示的平面直角坐标系,斜坡可以用一次函数y=x刻画.若小球到达的最高的点坐标为(6,12),解答下列问题:
(1)求抛物线的表达式;
(2)在斜坡OA上的B点有一棵树,B点的横坐标为3,树高为7,小球M能否飞过这棵树?通过计算说明理由;
(3)求小球M在飞行的过程中离斜坡OA的最大高度.
16.如图是某跳台滑雪训练场的横截面示意图,取某一位置的水平线为x轴,过跳台终点A作水平线的垂线为y轴,建立平面直角坐标系如图所示,图中的抛物线C1:y=﹣x2+40近似表示滑雪场地上的一座小山坡,某运动员从点O正上方50米处的A点滑出,滑出后沿一段抛物线C2:y=﹣x2+bx+c运动.当运动员运动到离A处的水平距离为60米时,离水平线的高度为60米.
(1)求小山坡最高点到水平线的距离.
(2)求抛物线C2所对应的函数表达式.
(3)当运动员滑出点A后,直接写出运动员运动的水平距离为多少米时,运动员与小山坡C1的竖直距离为10米?
17.飞机着陆后滑行的距离y(单位:m)关于滑行时间t(单位:s)的函数解析式是y=60t﹣t2.在飞机着陆滑行中,滑行最后的150m所用的时间是 s.
先根据关系列出函数式
1.有一人患了流感,经过2轮传染后,共有y人患了流感.假设每轮传染中,平均一个人传染了x个人,则y关于x的函数表达式为 .
2.销售某种商品,如果单价上涨m%,则售出的数量就减少,为了使该商品的销售金额最大,那么m的值应该确定为
3.某书店销售儿童书刊,一天可售出20套,每套盈利40元,为了扩大销售,增加盈利,尽快减少库存,书店决定采取降价措施.若一套书每降价1元,平均每天可多售出2套.设每套书降价x元时,书店一天可获利润y元.
(1)求y关于x的函数表达式.
(2)若要书店每天盈利1200元,则需降价多少元?
(3)当每套书降价多少元时,书店一天可获最大利润?最大利润为多少?
4.如图,点P,Q分别是边长为1cm的正方形ABCD的边BC和对角线AC上的两个动点,点P从B出发,朝BC方向运动,速度为1cm/s;点Q从A出发,朝AC方向运动,速度为cm/s,只要有一点运动到点C,两点就停止动.设运动的时间为x(s),△APQ的面积为y(cm2).
(1)求y关于x的函数解析式及自变量x的取值范围;
(2)在运动过程中,能否使△APQ的面积为正方形ABCD的面积的六分之一?若能,求x值;若不能,请说明理由.
5.如图,在矩形ABCD中,AB=6cm,BC=12cm,点P从点A出发,沿AB边向点B以1cm/s的速度移动,同时点Q从点B出发沿BC边向点C以2cm/s的速度移动,如果P,Q两点同时出发,分别到达B,C两点后就停止移动.设△PQD的面积为S,点移动的时间为x(x>0)
(1)求S关于x的函数表达式及自变量x的取值范围;
(2)经过多少时间,△PQD的面积最小?
6.某公司对办公大楼一块墙面进行如图所示的图案设计.这个图案由四个全等的直角三角形和一个小正方形拼接而成的大正方形,设小正方形的边长m,直角三角形较短直角边长n,且n=m﹣2,大正方形的面积为S.
(1)求S关于m的函数关系式;
(2)若小正方形边长不大于3,当大正方形面积最大时,求m的值.
7.某位同学做实验考查电流变化情况时,可以选择若干定值电阻进行并联,(假设可以选择任何数值的电阻),已知电源电压U为3V.(注:公式I,其中I是电流强度,U是电压,R是电阻)
(1)若只选择一个电阻,测得电流强度I为0.1A,求该电阻R的值.
(2)若所选的两个电阻分别为R1,R2,且R1+R2=20Ω,恰好使总电流强度I最小,求对应电阻R1,R2的值.(注:并联时总电阻R)(在求对应R1,R2的值时,用数学的方法书写过程)
8.某公园在人工湖里建造一道喷泉拱门,工人在垂直于湖面的立柱上安装喷头,从喷头喷出的水柱的形状可以看作是抛物线的一部分.安装后,通过测量获得如下数据,喷头高出湖面3米,在距立柱水平距离为d米的地点,水柱距离湖面高度为h米.
d(米) 0.50 1.00 1.50 2.00 2.50 3.00
h(米) 3.75 4.00 3.75 3.00 1.75 0
请解决以下问题:
(1)在网格中建立适当的平面直角坐标系,根据已知数据描点,并用平滑的曲线连接;
(2)结合表中所给数据或所画图象,直接写出水柱最高点距离湖面的高度;
(3)求h关于d的函数表达式;
(4)公园希望游船能从喷泉拱门下穿过,已知游船的宽度约为2米,游船的平顶棚到湖面的高度约为1米,从安全的角度考虑,要求游船到立柱的水平距离不小于1米,顶棚到水柱的竖直距离也不小于1米.工人想只通过调整喷头距离湖面的高度(不考虑其他因素)就能满足上述要求,请通过计算说明应如何调整.
.
参考答案:
一、
2
2.(1)∴抛物线解析式:y=﹣3(x+1)2+2
(2)∴抛物线解析式y=﹣(x+2)(x﹣4)
3.y=﹣x2+2x+3;沿y轴向上平移6个单位长度
4.(1)点B的坐标为(1,3).(2)y=x2+x.(3).
5.(1)抛物线的解析式为y=x2﹣x+2.5(0≤x≤4).(2)绳子最低点离地面的距离米.
6.解:(1)此抛物线的解析式为y=+6;
(2)当x=±3时,y=+6=4.92>4.5,
即这辆货运卡车能顺利通过隧道.
7.解:(1)y=﹣(x﹣4)2+3,当x=0时,y=﹣×16+3=3﹣=<2.44米,
故能射中球门;(2)当x=2时,y=﹣(2﹣4)2+3=>2.52,
∴守门员乙不能阻止球员甲的此次射门,
当y=2.52时,y=﹣(x﹣4)2+3=2.52,
解得:x1=1.6,x2=6.4(舍去),∴2﹣1.6=0.4(m),
答:他至少后退0.4m,才能阻止球员甲的射门.
8.解:(1)设抛物线的解析式为y=ax2+3.75,
把(1.5,3.05)代入得a×1.52+3.75=3.05,解得a=﹣,
所以抛物线的解析式为y=﹣x2+3.75(﹣2.5≤x≤1.5);
(2)当x=2﹣2.5=﹣0.5时,y=﹣×(﹣0.5)2+3.75≈3.69,
∵3.15m<3.69m,
∴在离投篮甲球员2米处时起跳,不能成功封盖住此次投篮;
(3)当y=3.15时,﹣x2+3.75=3.15,
解得x=±1.40,∵﹣2.5≤x≤1.5,∴x=﹣1.40,∴﹣1.40﹣(﹣2.5)=1.1,∴若乙球员想要成功封盖甲球员的这次投篮,他离甲球员的距离至多要1.1米.
9.解:(1)由题意得:
p点的坐标为(0,1.5),顶点坐标为(4,3.1)
则y=a(x﹣4)2+3.1,将P点坐标代入表达式得:
1.5=a(0﹣4)2+3.1,a=﹣0.1
故:y=﹣0.1(x﹣4)2+3.1.
(2)设y=﹣0.1(x﹣4)2+3.1=0,
解得:x=4+<12
故:此球不出界.
(3)先求乙恰好扣中的情况,当h=2时,即y=2
y=﹣0.1(x﹣4)2+3.1=2
解得:x=4±=m
但扣球点必须在球网右边即m>5,故4﹣舍去,
∴5米<m米<4+
10.(1)设y关于x的函数关系式为y=ax2+bx,依题可知:当x=1时,y=2.44;当x=3时,y=0,解得a、b;
(2)令y=4.88,解得方程,
(3)令y=2.44,解得x,然后求速度.
(1)∴y=﹣1.22x2+3.66x.
(2)不能.
理由:∵y=4.88,
∴4.88=﹣1.22x2+3.66x,(6分)
∴x2﹣3x+4=0.
∵(﹣3)2﹣4×4<0,
∴方程4.88=﹣1.22x2+3.66x无解.
∴足球的飞行高度不能达到4.88m.
(3)∵y=2.44,
∴2.44=﹣1.22x2+3.66x,∴x2﹣3x+2=0,
∴x1=1(不合题意,舍去),x2=2.
∴平均速度至少为(m/s).
11.(1)故抛物线解析式为:;
(2)当S=30时,30=t(t﹣4),解得:t1=10,t2=﹣6(舍去);
(3)由图象可得出:当t>2时,S随t的增大而增大,所以从第3个月起开始盈利,
所获利润为S(3)﹣S(2)=×3×(3﹣4)﹣×2×(2﹣4)=0.5(万元).
9.1
13.解:(1)∵y=﹣x2+2x+=﹣(x﹣1)2+,
∴该二次函数的顶点坐标为(1,),
∴水流喷出的最大高度是米,此时的水平距离为1米;
(2)令y=0,则﹣(x﹣1)2+=0,
解得x=2.5或x=﹣0.5(舍去)
所以水池的半径至少为2.5m,才能使喷出的水流不落在池外;
14.解:(1)y=4x﹣x2,该函数的对称轴为:x=4,
当x=4时,y=8,即点B(4,8);
(2)联立y=4x﹣x2、y=x并解得:x=7,故点A的坐标为:(7,).
15.解:(1)设抛物线的表达式为y=a(x﹣6)2+12,
∵该抛物线过点(0,0),
∴0=a(x﹣6)2+12,
解得a=﹣,
即抛物线的表达式为y=﹣(x﹣6)2+12;
(2)小球M能否飞过这棵树,
理由:当x=3时,y=×3=1,
∴此时小树顶端距离地面的高度为1+7=8(米),
当x=3时,y=﹣(3﹣6)2+12=9,
∵8<9,
∴小球M能否飞过这棵树;
(3)设小球M在飞行的过程中离斜坡OA的高度为h,
由题意可得:h=﹣(x﹣6)2+12﹣x=﹣(x﹣)2+,
∴当x=时,h取得最大值,此时h=,
答:小球M在飞行的过程中离斜坡OA的最大高度是米.
16.(1)由,
当x=0时,y有最大值为40.
∴小山坡最高点到水平线的距离为40米;
(2)把(0,50)、(60,60)代入,
得
解得
∴抛物线C2所对应的函数表达式;
(3)设运动员运动的水平距离是x米,此时小山坡的高度是y=﹣x2+40,运动员运动的水平高度是,
∴﹣x2+x+50=﹣x2+40+10,解得x=或0(舍去),
答:运动员运动的水平距离为为米时,运动员与小山坡C1的竖直距离为10米.
10
二、
y=(1+x)2.
25
3.(1)设每套书降价x元时,所获利润为y元,
y=(40﹣x)(20+2x)=﹣2x2+80x﹣20x+800=﹣2x2+60x+800;
(2)若每天盈利1200元,为了尽快减少库存,则应降价20元;
(3)当将价15元时,该书店可获得最大利润1250元.
4.(1)∴y=﹣x2+x(0<x<1);
(2)根据题意得,﹣x2+x=×1,整理得,3x2﹣3x+1=0,
∵Δ=(﹣3)2﹣4×3×1=﹣3<0,∴方程没有实数根,∴这样的点不存在.
5.解:(1)∴S=x2﹣6x+36(0<x≤6);(2)∵S=x2﹣6x+36=(x﹣3)2+27,1>0,∴当x=3时,S最小;即经过3s时,△PQD的面积最小.
6.(1)∴S关于m的函数关系式为S=5m2﹣12m+8(m>2);
(2)由(1)知,S=5m2﹣12m+8=5(m﹣1.2)2+0.8,
∵S关于m的二次函数的对称轴为直线m=1.2,二次项系数为正,
∴当2<m≤3时,S随m的增大而增大,
∴当m=3时,S最大.
∴当大正方形面积最大时,m=3.
7.解:(1)根据题意知:U=3V,I=0.1A.
∴.
(2)∵R1+R2=20Ω.
∴并联时总电阻R.
∵I.
∴总电流强度I.
故当R1=10Ω时,总电流强度I取最小值,此时R2=10Ω.
即:恰好使总电流强度I最小,对应电阻R1,R2的值都为10Ω.
8.解:(1)如图,
(2)水柱最高点距离湖面的高度是4米;
(3)由图象可得,顶点(1,4),
设二次函数的关系式为h=a(d﹣1)2+4,
把(2,3)代入可得a=﹣1,
所以h=﹣(d﹣1)2+4;
(4)设水枪高度向上调整m米,
设平移后二次函数关系式为h′=﹣(d﹣1)2+4+m,
当d=1+2=3时,h′=﹣4+4+m=m,
∴m≥2,
答:水枪高度至少向上调整2米.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
二次函数应用专题复习卷
函数类型确定的求二次函数表达式及简单的实际应用
1.已知二次函数y=(m﹣2)x2﹣4x+2m﹣8的图象经过原点,它可以由抛物线y=ax2(a≠0)平移得到,则a的值是 .
2.根据下列条件,求二次函数的解析式
(1)已知二次函数的图象经过点(﹣2,﹣1),且当x=﹣1时,函数有最大值2;
(2)抛物线的对称轴是直线x=1,与x轴的一个交点为(﹣2,0),与y轴交于点(0,12).
已知二次函数y=﹣x2+bx+c的图象过B(﹣1,0),C(2,3)两点.
(1)求此二次函数的表达式.
(2)若此抛物线沿y轴平移一次后过点(﹣2,1),试确定这次平移的方向和距离.
4.在平面直角坐标系中,△AOB的位置如图所示,已知∠AOB=90°,AO=BO,点A的坐标为(﹣3,1).
(1)求点B的坐标;
(2)求过A,O,B三点的抛物线的解析式;
(3)设点B关于抛物线的对称轴l的对称点为B1,求△AB1B的面积.
5.如图,小明的爸爸在相距4m的两树等高位置处拴了一根绳子,做成一个简易的秋千,绳子自然下垂呈抛物线,已知身高1.5m的小明站在距离树1m的地方,头部刚好触到绳子.
(1)求抛物线的函数表达式和自变量的取值范围.
(2)求绳子最低点离地面的距离.
6.如图,一隧道的横截面是由一段抛物线及矩形的三边围成的,隧道宽BC=10米,矩形部分高AB=3米,抛物线型的最高点E离地面OE=6米,按如图建立一个以BC为x轴,OE为y轴的直角坐标系.
(1)求抛物线的解析式;
(2)如果该隧道内设有双车道,现有一辆货运卡车高4.5米,宽3米,这辆货运卡车能顺利通过隧道吗?
7. 如图,在某场足球比赛中,球员甲从球门底部中心点O的正前方10m处起脚射门,足球沿抛物线飞向球门中心线;当足球飞离地面高度为3m时达到最高点,此时足球飞行的水平距离为6m.已知球门的横梁高OA为2.44m.
(1)在如图所示的平面直角坐标系中,问此飞行足球能否进球门?(不计其它情况)
(2)守门员乙站在距离球门2m处,他跳起时手的最大摸高为2.52m,他能阻止球员甲的此次射门吗?如果不能,他至少后退多远才能阻止球员甲的射门?
在一场篮球比赛中,甲球员在距篮4米处跳投,球运行的路线是抛物线,当球运行的水平距离为2.5米时,达到最大高度3.75米,然后球准确落入篮圈.已知篮圈中心到地面的距离为3.05米.
(1)建立如图所示的平面直角坐标系,求抛物线的解析式;
(2)乙球员身高为1.91米,跳起能摸到的高度为3.15米,此时他上前封盖,在离投篮甲球员2米处时起跳,问能否成功封盖住此次投篮?
(3)在(2)条件下若乙球员想要成功封盖甲球员的这次投篮,他离甲球员的距离至多要多少米?
9.小宇和佳佳两人进行羽毛球比赛,小宇发出一颗十分关键的球,出手点为P,P点距离地面的高度为1.5米,羽毛球的运动轨迹是抛物线,并且在距P点水平距离4米处达到最高点,最高点距离地面3.1米,建立如图所示的直角坐标系.
(1)求羽毛球飞行过程中,距地面高度y(米)与飞出的水平距离x(米)之间的函数关系;
(2)已知P点距离小宇对面的场地边线为12米,若佳佳不接球,此球是否会出界?说明理由;
(3)已知球网AB距点O的水平距离是5米,佳佳扣球的最大高度为2米,设佳佳的起跳点C的横坐标为m,若佳佳原地起跳,因佳佳扣球的最大高度(用线段CD表示)低于球的高度而导致扣球失败,求m的取值范围.
10.足球比赛中,某运动员将在地面上的足球对着球门踢出,图中的抛物线是足球的飞行高度y(m)关于飞行时间x(s)的函数图象(不考虑空气的阻力),已知足球飞出1s时,足球的飞行高度是2.44m,足球从飞出到落地共用3s.
(1)求y关于x的函数关系式;
(2)足球的飞行高度能否达到4.88米?请说明理由;
(3)假设没有拦挡,足球将擦着球门左上角射入球门,球门的高为2.44m(如图所示,足球的大小忽略不计).如果为了能及时将足球扑出,那么足球被踢出时,离球门左边框12m处的守门员至少要以多大的平均速度到球门的左边框?
11.某公司推出了一种高效环保型洗涤用品,年初上市后,公司经历了从亏损到盈利的过程,如图的二次函数图象(部分)刻画了该公司年初以来累积利润s(万元)与时间t(月)之间的关系(即前t个月的利润总和s与t之间的关系).根据图象提供的信息,解答下列问题:
(1)求累积利润s(万元)与时间t(月)之间的函数关系式;
(2)求截止到几月末公司累积利润可达30万元;
(3)从第几个月起公司开始盈利?该月公司所获利润是多少万元?
12.如图,有一个横截面边缘为抛物线的隧道入口,隧道入口处的底面宽度为8m,两侧距底面4m高处各有一盏灯,两灯间的水平距离为6m,则这个隧道入口的最大高度为 m(精确到0.1m).
13.如图,一个圆形喷水池的中央竖直安装了一个柱形喷水装置OA,A处的喷头向外喷水,水流在各个方向上沿形状相同的抛物线路径落下,水流喷出的高度y(m)与水平距离x(m)之间的关系式是y=﹣x2+2x+(x>0)
(1)求水流喷出的最大高度是多少m?此时的水平距离是多少m?
(2)若不计其他因素,水池的半径OB至少为多少m,才能使喷出的水流不落在池外?
14.如图,一个网球从斜坡OA的点O处抛出,网球运动路径的函数表达式是y=4x﹣x2,斜坡的函数表达式是y=x,其中y是高度,x是网球与点O之间的水平距离.
(1)求网球到达的最高点B的坐标.
(2)若网球落在斜坡上的点A处,求点A的坐标.
15.如图,一小球M从斜坡OA上的O点处抛出,球的抛出路线是抛物线的一部分,建立如图所示的平面直角坐标系,斜坡可以用一次函数y=x刻画.若小球到达的最高的点坐标为(6,12),解答下列问题:
(1)求抛物线的表达式;
(2)在斜坡OA上的B点有一棵树,B点的横坐标为3,树高为7,小球M能否飞过这棵树?通过计算说明理由;
(3)求小球M在飞行的过程中离斜坡OA的最大高度.
16.如图是某跳台滑雪训练场的横截面示意图,取某一位置的水平线为x轴,过跳台终点A作水平线的垂线为y轴,建立平面直角坐标系如图所示,图中的抛物线C1:y=﹣x2+40近似表示滑雪场地上的一座小山坡,某运动员从点O正上方50米处的A点滑出,滑出后沿一段抛物线C2:y=﹣x2+bx+c运动.当运动员运动到离A处的水平距离为60米时,离水平线的高度为60米.
(1)求小山坡最高点到水平线的距离.
(2)求抛物线C2所对应的函数表达式.
(3)当运动员滑出点A后,直接写出运动员运动的水平距离为多少米时,运动员与小山坡C1的竖直距离为10米?
17.飞机着陆后滑行的距离y(单位:m)关于滑行时间t(单位:s)的函数解析式是y=60t﹣t2.在飞机着陆滑行中,滑行最后的150m所用的时间是 s.
先根据关系列出函数式
1.有一人患了流感,经过2轮传染后,共有y人患了流感.假设每轮传染中,平均一个人传染了x个人,则y关于x的函数表达式为 .
2.销售某种商品,如果单价上涨m%,则售出的数量就减少,为了使该商品的销售金额最大,那么m的值应该确定为
3.某书店销售儿童书刊,一天可售出20套,每套盈利40元,为了扩大销售,增加盈利,尽快减少库存,书店决定采取降价措施.若一套书每降价1元,平均每天可多售出2套.设每套书降价x元时,书店一天可获利润y元.
(1)求y关于x的函数表达式.
(2)若要书店每天盈利1200元,则需降价多少元?
(3)当每套书降价多少元时,书店一天可获最大利润?最大利润为多少?
4.如图,点P,Q分别是边长为1cm的正方形ABCD的边BC和对角线AC上的两个动点,点P从B出发,朝BC方向运动,速度为1cm/s;点Q从A出发,朝AC方向运动,速度为cm/s,只要有一点运动到点C,两点就停止动.设运动的时间为x(s),△APQ的面积为y(cm2).
(1)求y关于x的函数解析式及自变量x的取值范围;
(2)在运动过程中,能否使△APQ的面积为正方形ABCD的面积的六分之一?若能,求x值;若不能,请说明理由.
5.如图,在矩形ABCD中,AB=6cm,BC=12cm,点P从点A出发,沿AB边向点B以1cm/s的速度移动,同时点Q从点B出发沿BC边向点C以2cm/s的速度移动,如果P,Q两点同时出发,分别到达B,C两点后就停止移动.设△PQD的面积为S,点移动的时间为x(x>0)
(1)求S关于x的函数表达式及自变量x的取值范围;
(2)经过多少时间,△PQD的面积最小?
6.某公司对办公大楼一块墙面进行如图所示的图案设计.这个图案由四个全等的直角三角形和一个小正方形拼接而成的大正方形,设小正方形的边长m,直角三角形较短直角边长n,且n=m﹣2,大正方形的面积为S.
(1)求S关于m的函数关系式;
(2)若小正方形边长不大于3,当大正方形面积最大时,求m的值.
7.某位同学做实验考查电流变化情况时,可以选择若干定值电阻进行并联,(假设可以选择任何数值的电阻),已知电源电压U为3V.(注:公式I,其中I是电流强度,U是电压,R是电阻)
(1)若只选择一个电阻,测得电流强度I为0.1A,求该电阻R的值.
(2)若所选的两个电阻分别为R1,R2,且R1+R2=20Ω,恰好使总电流强度I最小,求对应电阻R1,R2的值.(注:并联时总电阻R)(在求对应R1,R2的值时,用数学的方法书写过程)
8.某公园在人工湖里建造一道喷泉拱门,工人在垂直于湖面的立柱上安装喷头,从喷头喷出的水柱的形状可以看作是抛物线的一部分.安装后,通过测量获得如下数据,喷头高出湖面3米,在距立柱水平距离为d米的地点,水柱距离湖面高度为h米.
d(米) 0.50 1.00 1.50 2.00 2.50 3.00
h(米) 3.75 4.00 3.75 3.00 1.75 0
请解决以下问题:
(1)在网格中建立适当的平面直角坐标系,根据已知数据描点,并用平滑的曲线连接;
(2)结合表中所给数据或所画图象,直接写出水柱最高点距离湖面的高度;
(3)求h关于d的函数表达式;
(4)公园希望游船能从喷泉拱门下穿过,已知游船的宽度约为2米,游船的平顶棚到湖面的高度约为1米,从安全的角度考虑,要求游船到立柱的水平距离不小于1米,顶棚到水柱的竖直距离也不小于1米.工人想只通过调整喷头距离湖面的高度(不考虑其他因素)就能满足上述要求,请通过计算说明应如何调整.
.
参考答案:
一、
2
2.(1)∴抛物线解析式:y=﹣3(x+1)2+2
(2)∴抛物线解析式y=﹣(x+2)(x﹣4)
3.y=﹣x2+2x+3;沿y轴向上平移6个单位长度
4.(1)点B的坐标为(1,3).(2)y=x2+x.(3).
5.(1)抛物线的解析式为y=x2﹣x+2.5(0≤x≤4).(2)绳子最低点离地面的距离米.
6.解:(1)此抛物线的解析式为y=+6;
(2)当x=±3时,y=+6=4.92>4.5,
即这辆货运卡车能顺利通过隧道.
7.解:(1)y=﹣(x﹣4)2+3,当x=0时,y=﹣×16+3=3﹣=<2.44米,
故能射中球门;(2)当x=2时,y=﹣(2﹣4)2+3=>2.52,
∴守门员乙不能阻止球员甲的此次射门,
当y=2.52时,y=﹣(x﹣4)2+3=2.52,
解得:x1=1.6,x2=6.4(舍去),∴2﹣1.6=0.4(m),
答:他至少后退0.4m,才能阻止球员甲的射门.
8.解:(1)设抛物线的解析式为y=ax2+3.75,
把(1.5,3.05)代入得a×1.52+3.75=3.05,解得a=﹣,
所以抛物线的解析式为y=﹣x2+3.75(﹣2.5≤x≤1.5);
(2)当x=2﹣2.5=﹣0.5时,y=﹣×(﹣0.5)2+3.75≈3.69,
∵3.15m<3.69m,
∴在离投篮甲球员2米处时起跳,不能成功封盖住此次投篮;
(3)当y=3.15时,﹣x2+3.75=3.15,
解得x=±1.40,∵﹣2.5≤x≤1.5,∴x=﹣1.40,∴﹣1.40﹣(﹣2.5)=1.1,∴若乙球员想要成功封盖甲球员的这次投篮,他离甲球员的距离至多要1.1米.
9.解:(1)由题意得:
p点的坐标为(0,1.5),顶点坐标为(4,3.1)
则y=a(x﹣4)2+3.1,将P点坐标代入表达式得:
1.5=a(0﹣4)2+3.1,a=﹣0.1
故:y=﹣0.1(x﹣4)2+3.1.
(2)设y=﹣0.1(x﹣4)2+3.1=0,
解得:x=4+<12
故:此球不出界.
(3)先求乙恰好扣中的情况,当h=2时,即y=2
y=﹣0.1(x﹣4)2+3.1=2
解得:x=4±=m
但扣球点必须在球网右边即m>5,故4﹣舍去,
∴5米<m米<4+
10.(1)设y关于x的函数关系式为y=ax2+bx,依题可知:当x=1时,y=2.44;当x=3时,y=0,解得a、b;
(2)令y=4.88,解得方程,
(3)令y=2.44,解得x,然后求速度.
(1)∴y=﹣1.22x2+3.66x.
(2)不能.
理由:∵y=4.88,
∴4.88=﹣1.22x2+3.66x,(6分)
∴x2﹣3x+4=0.
∵(﹣3)2﹣4×4<0,
∴方程4.88=﹣1.22x2+3.66x无解.
∴足球的飞行高度不能达到4.88m.
(3)∵y=2.44,
∴2.44=﹣1.22x2+3.66x,∴x2﹣3x+2=0,
∴x1=1(不合题意,舍去),x2=2.
∴平均速度至少为(m/s).
11.(1)故抛物线解析式为:;
(2)当S=30时,30=t(t﹣4),解得:t1=10,t2=﹣6(舍去);
(3)由图象可得出:当t>2时,S随t的增大而增大,所以从第3个月起开始盈利,
所获利润为S(3)﹣S(2)=×3×(3﹣4)﹣×2×(2﹣4)=0.5(万元).
9.1
13.解:(1)∵y=﹣x2+2x+=﹣(x﹣1)2+,
∴该二次函数的顶点坐标为(1,),
∴水流喷出的最大高度是米,此时的水平距离为1米;
(2)令y=0,则﹣(x﹣1)2+=0,
解得x=2.5或x=﹣0.5(舍去)
所以水池的半径至少为2.5m,才能使喷出的水流不落在池外;
14.解:(1)y=4x﹣x2,该函数的对称轴为:x=4,
当x=4时,y=8,即点B(4,8);
(2)联立y=4x﹣x2、y=x并解得:x=7,故点A的坐标为:(7,).
15.解:(1)设抛物线的表达式为y=a(x﹣6)2+12,
∵该抛物线过点(0,0),
∴0=a(x﹣6)2+12,
解得a=﹣,
即抛物线的表达式为y=﹣(x﹣6)2+12;
(2)小球M能否飞过这棵树,
理由:当x=3时,y=×3=1,
∴此时小树顶端距离地面的高度为1+7=8(米),
当x=3时,y=﹣(3﹣6)2+12=9,
∵8<9,
∴小球M能否飞过这棵树;
(3)设小球M在飞行的过程中离斜坡OA的高度为h,
由题意可得:h=﹣(x﹣6)2+12﹣x=﹣(x﹣)2+,
∴当x=时,h取得最大值,此时h=,
答:小球M在飞行的过程中离斜坡OA的最大高度是米.
16.(1)由,
当x=0时,y有最大值为40.
∴小山坡最高点到水平线的距离为40米;
(2)把(0,50)、(60,60)代入,
得
解得
∴抛物线C2所对应的函数表达式;
(3)设运动员运动的水平距离是x米,此时小山坡的高度是y=﹣x2+40,运动员运动的水平高度是,
∴﹣x2+x+50=﹣x2+40+10,解得x=或0(舍去),
答:运动员运动的水平距离为为米时,运动员与小山坡C1的竖直距离为10米.
10
二、
y=(1+x)2.
25
3.(1)设每套书降价x元时,所获利润为y元,
y=(40﹣x)(20+2x)=﹣2x2+80x﹣20x+800=﹣2x2+60x+800;
(2)若每天盈利1200元,为了尽快减少库存,则应降价20元;
(3)当将价15元时,该书店可获得最大利润1250元.
4.(1)∴y=﹣x2+x(0<x<1);
(2)根据题意得,﹣x2+x=×1,整理得,3x2﹣3x+1=0,
∵Δ=(﹣3)2﹣4×3×1=﹣3<0,∴方程没有实数根,∴这样的点不存在.
5.解:(1)∴S=x2﹣6x+36(0<x≤6);(2)∵S=x2﹣6x+36=(x﹣3)2+27,1>0,∴当x=3时,S最小;即经过3s时,△PQD的面积最小.
6.(1)∴S关于m的函数关系式为S=5m2﹣12m+8(m>2);
(2)由(1)知,S=5m2﹣12m+8=5(m﹣1.2)2+0.8,
∵S关于m的二次函数的对称轴为直线m=1.2,二次项系数为正,
∴当2<m≤3时,S随m的增大而增大,
∴当m=3时,S最大.
∴当大正方形面积最大时,m=3.
7.解:(1)根据题意知:U=3V,I=0.1A.
∴.
(2)∵R1+R2=20Ω.
∴并联时总电阻R.
∵I.
∴总电流强度I.
故当R1=10Ω时,总电流强度I取最小值,此时R2=10Ω.
即:恰好使总电流强度I最小,对应电阻R1,R2的值都为10Ω.
8.解:(1)如图,
(2)水柱最高点距离湖面的高度是4米;
(3)由图象可得,顶点(1,4),
设二次函数的关系式为h=a(d﹣1)2+4,
把(2,3)代入可得a=﹣1,
所以h=﹣(d﹣1)2+4;
(4)设水枪高度向上调整m米,
设平移后二次函数关系式为h′=﹣(d﹣1)2+4+m,
当d=1+2=3时,h′=﹣4+4+m=m,
∴m≥2,
答:水枪高度至少向上调整2米.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
