浙教版八年级上册第2章 特殊三角形复习课 (共12张PPT)
文档属性
| 名称 | 浙教版八年级上册第2章 特殊三角形复习课 (共12张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 397.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-10 07:00:39 | ||
图片预览


文档简介
(共12张PPT)
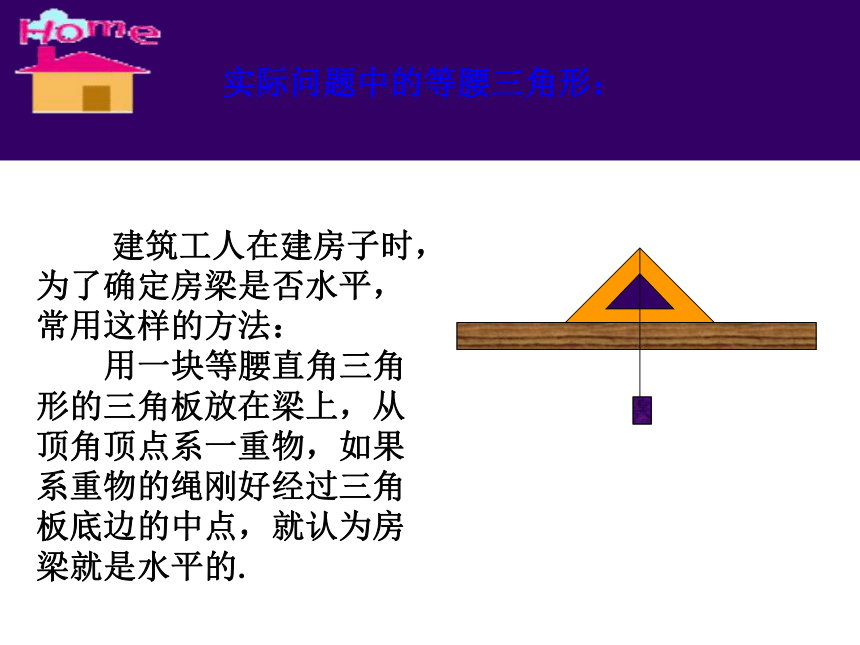
实际问题中的等腰三角形:
建筑工人在建房子时,为了确定房梁是否水平,常用这样的方法:
用一块等腰直角三角形的三角板放在梁上,从顶角顶点系一重物,如果系重物的绳刚好经过三角板底边的中点,就认为房梁就是水平的.
等腰三角形
等边对等角
三线合一
知识小结
等边三角形
判定方法:1.定义
2.判定定理
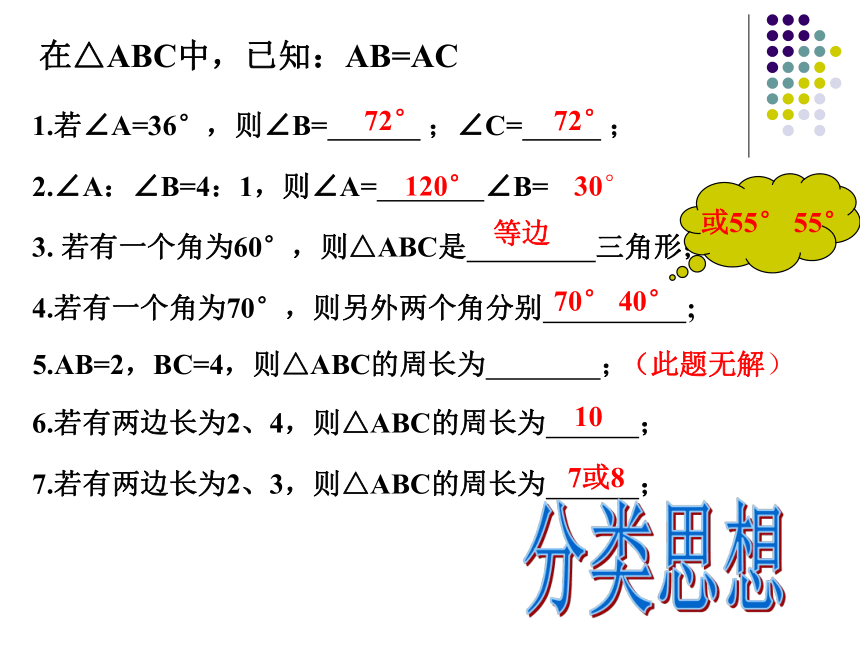
在△ABC中,已知:AB=AC
2.∠A:∠B=4:1,则∠A= ∠B=
4.若有一个角为70°,则另外两个角分别 ;
3. 若有一个角为60°,则△ABC是 三角形;
1.若∠A=36°,则∠B= ;∠C= ;
72°
72°
120°
30°
70° 40°
等边
或55° 55°
5.AB=2,BC=4,则△ABC的周长为 ;
(此题无解)
6.若有两边长为2、4,则△ABC的周长为 ;
10
7.若有两边长为2、3,则△ABC的周长为 ;
7或8
1、 角的分类
2 、边的分类
(在等腰三角形中)
在解等腰三角形的题目时,经常会运用分类思想讨论,以防止掉入数学“陷阱”!
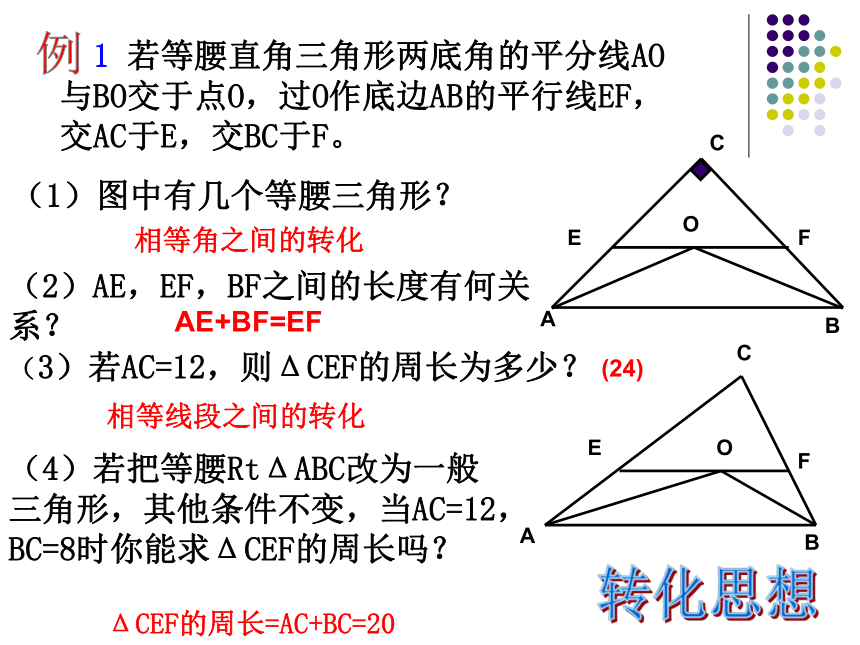
1 若等腰直角三角形两底角的平分线AO与BO交于点O,过O作底边AB的平行线EF,交AC于E,交BC于F。
(1)图中有几个等腰三角形?
(2)AE,EF,BF之间的长度有何关系?
(3)若AC=12,则ΔCEF的周长为多少?
AE+BF=EF
(24)
ΔCEF的周长=AC+BC=20
C
A
O
E
B
F
(4)若把等腰RtΔABC改为一般三角形,其他条件不变,当AC=12,BC=8时你能求ΔCEF的周长吗?
O
F
E
B
C
A
相等角之间的转化
相等线段之间的转化
角与角的转化: 相等角之间的代换.
边与角的转化: 等边对等角.
等角对等边.
3.边与边的转化: 相等线段之间进行代换
(在同一个三角形)
1、如果等腰三角形的一个外角为100°, 则这个等腰三角形的顶角为 。
2、如图,在三角形ABC中,BC=10,AD=BD,若三角形ACD的周长为18 , 则AC长为 。
B
A
C
D
20°或80°
(分类讨论)
8
(转化思想)
例2 如图,等边三角形ABC中,D是AC的中点,延长BC到点E,使CE=CD,DM ⊥BC于M,求证:BM=EM
A
B
C
D
E
M
例3 已知ΔABC的边BC上的中线是ΔABC的角平分线。求证: ΔABC是等腰三角形。
特殊三角形之一——等腰三角形
1.定义:有两边相等的三角形叫做等腰三角形。
2.性质
(1)等腰三角形是轴对称图形;
(2)在同一个三角形中,等边对等角;
(3)等腰三角形三线合一性质。
3.等腰三角形的判定定理:
在同一个三角形中,等角对等边。
特殊的等腰三角形——等边三角形
布置作业
1.作业本(1)复习题T1——4
2.课文P85T1-17
实际问题中的等腰三角形:
建筑工人在建房子时,为了确定房梁是否水平,常用这样的方法:
用一块等腰直角三角形的三角板放在梁上,从顶角顶点系一重物,如果系重物的绳刚好经过三角板底边的中点,就认为房梁就是水平的.
等腰三角形
等边对等角
三线合一
知识小结
等边三角形
判定方法:1.定义
2.判定定理
在△ABC中,已知:AB=AC
2.∠A:∠B=4:1,则∠A= ∠B=
4.若有一个角为70°,则另外两个角分别 ;
3. 若有一个角为60°,则△ABC是 三角形;
1.若∠A=36°,则∠B= ;∠C= ;
72°
72°
120°
30°
70° 40°
等边
或55° 55°
5.AB=2,BC=4,则△ABC的周长为 ;
(此题无解)
6.若有两边长为2、4,则△ABC的周长为 ;
10
7.若有两边长为2、3,则△ABC的周长为 ;
7或8
1、 角的分类
2 、边的分类
(在等腰三角形中)
在解等腰三角形的题目时,经常会运用分类思想讨论,以防止掉入数学“陷阱”!
1 若等腰直角三角形两底角的平分线AO与BO交于点O,过O作底边AB的平行线EF,交AC于E,交BC于F。
(1)图中有几个等腰三角形?
(2)AE,EF,BF之间的长度有何关系?
(3)若AC=12,则ΔCEF的周长为多少?
AE+BF=EF
(24)
ΔCEF的周长=AC+BC=20
C
A
O
E
B
F
(4)若把等腰RtΔABC改为一般三角形,其他条件不变,当AC=12,BC=8时你能求ΔCEF的周长吗?
O
F
E
B
C
A
相等角之间的转化
相等线段之间的转化
角与角的转化: 相等角之间的代换.
边与角的转化: 等边对等角.
等角对等边.
3.边与边的转化: 相等线段之间进行代换
(在同一个三角形)
1、如果等腰三角形的一个外角为100°, 则这个等腰三角形的顶角为 。
2、如图,在三角形ABC中,BC=10,AD=BD,若三角形ACD的周长为18 , 则AC长为 。
B
A
C
D
20°或80°
(分类讨论)
8
(转化思想)
例2 如图,等边三角形ABC中,D是AC的中点,延长BC到点E,使CE=CD,DM ⊥BC于M,求证:BM=EM
A
B
C
D
E
M
例3 已知ΔABC的边BC上的中线是ΔABC的角平分线。求证: ΔABC是等腰三角形。
特殊三角形之一——等腰三角形
1.定义:有两边相等的三角形叫做等腰三角形。
2.性质
(1)等腰三角形是轴对称图形;
(2)在同一个三角形中,等边对等角;
(3)等腰三角形三线合一性质。
3.等腰三角形的判定定理:
在同一个三角形中,等角对等边。
特殊的等腰三角形——等边三角形
布置作业
1.作业本(1)复习题T1——4
2.课文P85T1-17
同课章节目录
- 第1章 三角形的初步知识
- 1.1 认识三角形
- 1.2 定义与命题
- 1.3 证明
- 1.4 全等三角形
- 1.5 三角形全等的判定
- 1.6 尺规作图
- 第2章 特殊三角形
- 2.1 图形的轴对称
- 2.2 等腰三角形
- 2.3 等腰三角形的性质定理
- 2.4 等腰三角形的判定定理
- 2.5 逆命题和逆定理
- 2.6 直角三角形
- 2.7 探索勾股定理
- 2.8 直角三角形全等的判定
- 第3章 一元一次不等式
- 3.1 认识不等式
- 3.2 不等式的基本性质
- 3.3 一元一次不等式
- 3.4 一元一次不等式组
- 第4章 图形与坐标
- 4.1 探索确定位置的方法
- 4.2 平面直角坐标系
- 4.3 坐标平面内图形的轴对称和平移
- 第5章 一次函数
- 5.1 常量与变量
- 5.2 函数
- 5.3 一次函数
- 5.4 一次函数的图象
- 5.5 一次函数的简单应用
