浙教版数学八年级下册同步课件:2.4 一元二次方程根与系数的关系(选学)(共19张PPT)
文档属性
| 名称 | 浙教版数学八年级下册同步课件:2.4 一元二次方程根与系数的关系(选学)(共19张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 246.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-10 00:00:00 | ||
图片预览






文档简介
(共19张PPT)
第二章 一元二次方程
2.4 一元二次方程根与系数的关系
知识回顾
1.一元二次方程的一般形式是什么?
2.一元二次方程根的判别式是什么?
3.一元二次方程的求根公式是什么?
ax2+bx+c=0(a≠0);
b2-4ac
4.一元二次方程的根的情况怎样确定?
b2-4ac>0则方程ax2+bx+c=0(a≠0)有两个不相等的实数根;
b2-4ac=0则方程ax2+bx+c=0(a≠0)有两个相等的实数根;
b2-4ac<0则方程ax2+bx+c=0(a≠0)没有实数根.
获取新知
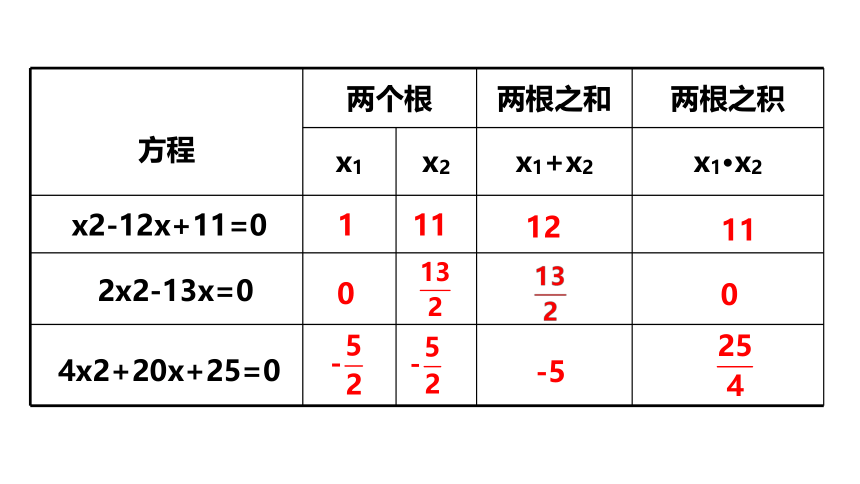
先解下列方程,然后计算这些方程的两根之和与两根之积:
(1)x2-12x+11=0
(2)2x2-13x=0
(3)4x2+20x+25=0
方程 两个根 两根之和 两根之积
x1 x2 x1+x2 x1·x2
x2-12x+11=0
2x2-13x=0
4x2+20x+25=0
1
11
12
11
0
0
-5
你可以发现什么结论?
一般地,一元二次方程的根与系数有如下关系:
如果x1,x2是一元二次方程 ax2+bx+c=0 的两个根,那么
x1+x2= ,x1·x2=
【注意】能用这个结论的前提为b2-4ac≥0
上面的结论对于任意的一元二次方程都适合的吗?
下面我们来证明这一结论。
设一元二次方程ax2+bx+c=0(b2-4ac≥0)的两个根为x1,x2
设一元二次方程ax2+bx+c=0(b2-4ac≥0)的两个根为x1,x2
例1 设x1,x2是一元二次方程5x2-7x-3=0的两个根,
求 x12+x22和的 值.
解:由一元二次方程的根与系数的关系,得
【总结归纳】求与方程的根有关的代数式的值时,一般先将所求的代数式化成含两根之和或两根之积的形式,再整体代入.
几种常见的求值:
解:设这个方程为3x2+bx+c=0,由一元二次方程根与系数的关系,得
所以这个一元二次方程是3x2-4x+1=0.
例2 已知一个一元二次方程的二次项系数是3,它的两个根分别是 ,1. 写出这个方程.
【拓展延伸】
一元二次方程根与系数的关系还有两个重要推论。
推论1:若方程x2+px+q=0的两根为x1,x2,则有x1+x2=-p,
x1·x2=q.
推论2:以x1,x2为根的一元二次方程(二次项系数为1)是
x2+(x1+x2)x+x1·x2=0
使用根与系数的关系公式应注意三点
(1)正确找到方程中a,b,c的值,其中a≠0;
(2)根的判别式应大于或等于零;
(3)用根与系数的关系求待定字母的值时,求出的值一定要进行检验,注意取舍.
随堂演练
D
1.一元二次方程x2-2x=0的两根分别为x1和x2,则x1x2为 ( )
A.-2 B.1 C.2 D.0
2.已知关于x的一元二次方程x2-3x+m=0的两根分别为x1,x2,则x1+x2的值为 ( )
A.-3 B.3 C.m D.-m
B
3.利用根与系数的关系,求下列方程的两根之和、两根之积.
(1)x2 + 7x + 6 = 0;(2)2x2 - 3x - 2 = 0.
解:(1)这里 a = 1 , b = 7 , c = 6.
Δ = b2 - 4ac = 72 – 4 × 1 × 6 = 25 > 0.
∴方程有两个实数根.
设方程的两个实数根是 x1, x2, 那么
x1 + x2 = -7 , x1 x2 = 6.
(2)2x2 - 3x - 2 = 0.
(2)这里 a = 2 , b = -3 , c = -2.
Δ= b2 - 4ac = (- 3)2 – 4 × 2 × (-2) = 25 > 0,
∴方程有两个实数根.
设方程的两个实数根是 x1, x2, 那么
x1 + x2 = , x1 x2 = -1 .
4.已知关于x的一元二次方程x2+3x+m-1=0有两个实数根分别为x1,x2.
(1)求m的取值范围;
(2)若2(x1+x2)+x1x2+10=0,求m的值.
(2)由已知可得x1+x2=-3,x1x2=m-1.
又∵2(x1+x2)+x1x2+10=0,
∴2×(-3)+m-1+10=0,
∴m=-3.
根与系数的关系
(韦达定理)
内 容
如果一元二次方程 ax2+bx+c=0(a≠0)的两个根分别是x1、 x2,那么
应 用
第二章 一元二次方程
2.4 一元二次方程根与系数的关系
知识回顾
1.一元二次方程的一般形式是什么?
2.一元二次方程根的判别式是什么?
3.一元二次方程的求根公式是什么?
ax2+bx+c=0(a≠0);
b2-4ac
4.一元二次方程的根的情况怎样确定?
b2-4ac>0则方程ax2+bx+c=0(a≠0)有两个不相等的实数根;
b2-4ac=0则方程ax2+bx+c=0(a≠0)有两个相等的实数根;
b2-4ac<0则方程ax2+bx+c=0(a≠0)没有实数根.
获取新知
先解下列方程,然后计算这些方程的两根之和与两根之积:
(1)x2-12x+11=0
(2)2x2-13x=0
(3)4x2+20x+25=0
方程 两个根 两根之和 两根之积
x1 x2 x1+x2 x1·x2
x2-12x+11=0
2x2-13x=0
4x2+20x+25=0
1
11
12
11
0
0
-5
你可以发现什么结论?
一般地,一元二次方程的根与系数有如下关系:
如果x1,x2是一元二次方程 ax2+bx+c=0 的两个根,那么
x1+x2= ,x1·x2=
【注意】能用这个结论的前提为b2-4ac≥0
上面的结论对于任意的一元二次方程都适合的吗?
下面我们来证明这一结论。
设一元二次方程ax2+bx+c=0(b2-4ac≥0)的两个根为x1,x2
设一元二次方程ax2+bx+c=0(b2-4ac≥0)的两个根为x1,x2
例1 设x1,x2是一元二次方程5x2-7x-3=0的两个根,
求 x12+x22和的 值.
解:由一元二次方程的根与系数的关系,得
【总结归纳】求与方程的根有关的代数式的值时,一般先将所求的代数式化成含两根之和或两根之积的形式,再整体代入.
几种常见的求值:
解:设这个方程为3x2+bx+c=0,由一元二次方程根与系数的关系,得
所以这个一元二次方程是3x2-4x+1=0.
例2 已知一个一元二次方程的二次项系数是3,它的两个根分别是 ,1. 写出这个方程.
【拓展延伸】
一元二次方程根与系数的关系还有两个重要推论。
推论1:若方程x2+px+q=0的两根为x1,x2,则有x1+x2=-p,
x1·x2=q.
推论2:以x1,x2为根的一元二次方程(二次项系数为1)是
x2+(x1+x2)x+x1·x2=0
使用根与系数的关系公式应注意三点
(1)正确找到方程中a,b,c的值,其中a≠0;
(2)根的判别式应大于或等于零;
(3)用根与系数的关系求待定字母的值时,求出的值一定要进行检验,注意取舍.
随堂演练
D
1.一元二次方程x2-2x=0的两根分别为x1和x2,则x1x2为 ( )
A.-2 B.1 C.2 D.0
2.已知关于x的一元二次方程x2-3x+m=0的两根分别为x1,x2,则x1+x2的值为 ( )
A.-3 B.3 C.m D.-m
B
3.利用根与系数的关系,求下列方程的两根之和、两根之积.
(1)x2 + 7x + 6 = 0;(2)2x2 - 3x - 2 = 0.
解:(1)这里 a = 1 , b = 7 , c = 6.
Δ = b2 - 4ac = 72 – 4 × 1 × 6 = 25 > 0.
∴方程有两个实数根.
设方程的两个实数根是 x1, x2, 那么
x1 + x2 = -7 , x1 x2 = 6.
(2)2x2 - 3x - 2 = 0.
(2)这里 a = 2 , b = -3 , c = -2.
Δ= b2 - 4ac = (- 3)2 – 4 × 2 × (-2) = 25 > 0,
∴方程有两个实数根.
设方程的两个实数根是 x1, x2, 那么
x1 + x2 = , x1 x2 = -1 .
4.已知关于x的一元二次方程x2+3x+m-1=0有两个实数根分别为x1,x2.
(1)求m的取值范围;
(2)若2(x1+x2)+x1x2+10=0,求m的值.
(2)由已知可得x1+x2=-3,x1x2=m-1.
又∵2(x1+x2)+x1x2+10=0,
∴2×(-3)+m-1+10=0,
∴m=-3.
根与系数的关系
(韦达定理)
内 容
如果一元二次方程 ax2+bx+c=0(a≠0)的两个根分别是x1、 x2,那么
应 用
同课章节目录
- 第一章 二次根式
- 1.1 二次根式
- 1.2 二次根式的性质
- 1.3 二次根式的运算
- 第二章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程的应用
- 2.4 一元二次方程根与系数的关系(选学)
- 第三章 数据分析初步
- 3.1 平均数
- 3.2 中位数和众数
- 3.3 方差和标准差
- 第四章 平行四边形
- 4.1 多边形
- 4.2 平行四边形
- 4.3 中心对称
- 4.4 平行四边形的判定
- 4.5 三角形的中位线
- 4.6 反证法
- 第五章 特殊平行四边形
- 5.1 矩形
- 5.2 菱形
- 5.3 正方形
- 第六章 反比例函数
- 6.1 反比例函数
- 6.2 反比例函数的图象和性质
- 6.3 反比例函数的应用
