浙教版八年级下册4.1.2多边形的内角和课件(共15张PPT)
文档属性
| 名称 | 浙教版八年级下册4.1.2多边形的内角和课件(共15张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 241.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-10 00:00:00 | ||
图片预览





文档简介
(共15张PPT)
第四章 平行四边形
4.1.2 多边形的内角和
知识回顾
在同一平面内
多边形:_____________,由任意两条都不在同一条直线上的若干条线段(线段的条数不小于__)首尾顺次相接形成的图形叫做多边形.
边:组成多边形的各条线段叫做多边形的边.
内角:多边形相邻两边组成的角叫做多边形的内角.
对角线:连结多边形不相邻两个顶点的线段叫做多边形的对角线.
3
外角:多边形一边的延长线与相邻的另一边所组成的角叫做多边形的外角.
顶点:多边形每一个内角的顶点叫做多边形的顶点.
对角线:连结多边形不相邻两个顶点的线段叫做多边形的对角线.
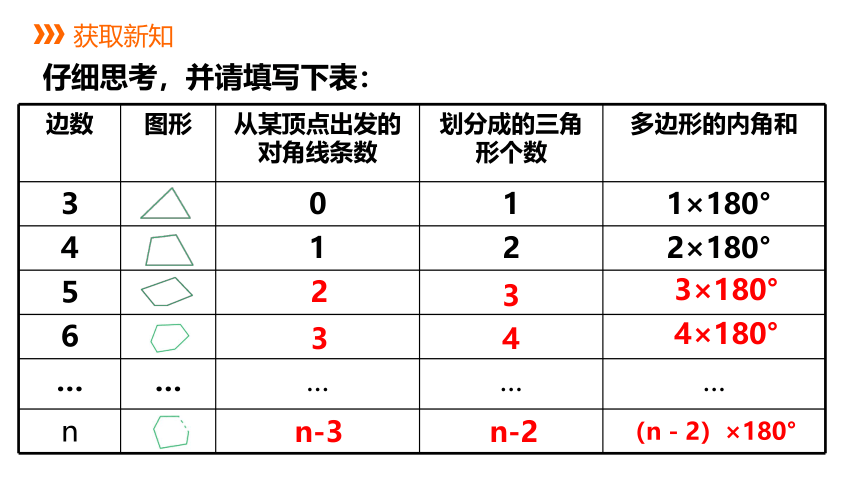
获取新知
仔细思考,并请填写下表:
边数 图形 从某顶点出发的对角线条数 划分成的三角形个数 多边形的内角和
3 0 1 1×180°
4 1 2 2×180°
5
6
… … … … …
n
2
3
3
4
3×180°
4×180°
n-3
n-2
(n-2)×180°
对于n边形,从某一个顶点出发的__________条对角线把n边形分成__________个三角形,所以n边形的内角和就等于这__________个三角形的所有内角之和
(n-3)
(n-2)
(n-2)
于是就有下面的定理:
n边形的内角和为(n-2)×180°(n≥3)
我们可以发现
求十边形的内角和.
已知一个多边形的内角和为900°,这个多边形是几边形?
1440
七边形
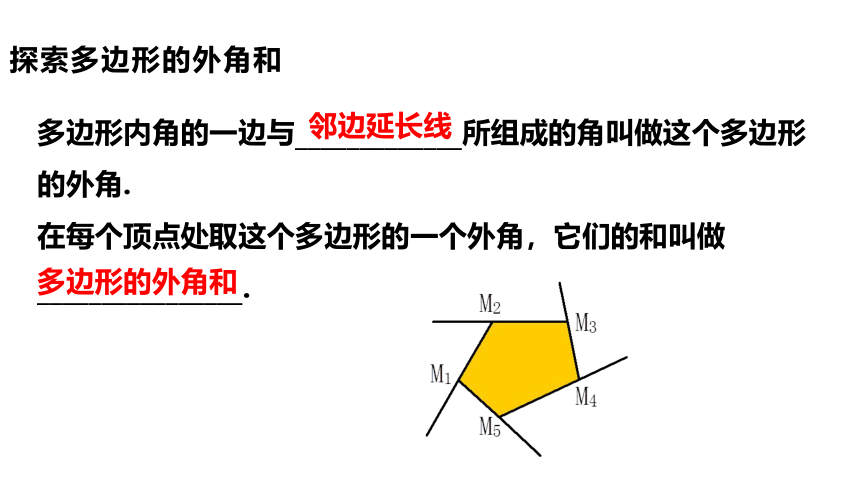
探索多边形的外角和
多边形内角的一边与_____________所组成的角叫做这个多边形的外角.
在每个顶点处取这个多边形的一个外角,它们的和叫做________________.
邻边延长线
多边形的外角和
怎样求三角形的外角和?
四边形的外角和呢?
五边形的外角和呢?
定理:任意多边形的外角和都为360°.
多边形的边数 3 4 5 6 … n
多边形的内角与外角的总和 …
多边形的内角和 …
多边形的外角和 …
540°
720°
900°
1080°
180°
360°
540°
720°
360°
360°
360°
360°
n×180°
(n-2)×180°
360°
已知六边形的各内角相等,问:各内角、外角分别是多少度?
已知多边形的内角和与外角和相等,那么它是几边形?
四边形
内角:120o
外角:60o
例2 一个六边形如图4-5.已知AB//DE,BC//EF,CD//AF.
求∠A+∠C+∠E的度数.
分析:因为两条平行线被一条直线所截,有许多等角关系,所以我们不妨连结AD试试看,如图.不难发现,∠1=∠3,∠2=∠4.由此可得本题解法.
∠FAB+∠C+∠E= ×720 ° =360 ° .
解 如图,连结AD.
∵AB//DE,CD//AF(已知),
∴∠1=∠3,∠2=∠4.
∴∠1+∠2=∠3+∠4,即∠FAB=∠CDE.
同理,∠B=∠E,∠C=∠F.
∵∠FAB+∠B+∠C+∠CDE+∠E+∠F
=(6-2) × 180 ° =720 ° ,
多边形
n边形的内角和为____________
过n边形的同一顶点可以引_______条对角线;n边形共有_______条对角线
任意多边形的外角和为_________
(n-2)×180°
360°
(n-3)
随堂演练
1.[2019·云南] 一个十二边形的内角和等于( )
A.2160° B.2080° C.1980° D.1800°
2.[2018·宁波期中] 若一个多边形的内角和等于1260°,则该多边形的边数是 ( )
A.8 B.9 C.10 D.11
D
B
3.[2018·绍兴期中] 如果n边形的内角和等于外角和的3倍,那么n的值是 ( )
A.5 B.6 C.7 D.8
4.已知一个多边形的每个内角都相等.若这个多边形的内角和为540°,则这个多边形的每一个外角等于 ( )
A.60° B.72° C.90° D.108°
D
B
第四章 平行四边形
4.1.2 多边形的内角和
知识回顾
在同一平面内
多边形:_____________,由任意两条都不在同一条直线上的若干条线段(线段的条数不小于__)首尾顺次相接形成的图形叫做多边形.
边:组成多边形的各条线段叫做多边形的边.
内角:多边形相邻两边组成的角叫做多边形的内角.
对角线:连结多边形不相邻两个顶点的线段叫做多边形的对角线.
3
外角:多边形一边的延长线与相邻的另一边所组成的角叫做多边形的外角.
顶点:多边形每一个内角的顶点叫做多边形的顶点.
对角线:连结多边形不相邻两个顶点的线段叫做多边形的对角线.
获取新知
仔细思考,并请填写下表:
边数 图形 从某顶点出发的对角线条数 划分成的三角形个数 多边形的内角和
3 0 1 1×180°
4 1 2 2×180°
5
6
… … … … …
n
2
3
3
4
3×180°
4×180°
n-3
n-2
(n-2)×180°
对于n边形,从某一个顶点出发的__________条对角线把n边形分成__________个三角形,所以n边形的内角和就等于这__________个三角形的所有内角之和
(n-3)
(n-2)
(n-2)
于是就有下面的定理:
n边形的内角和为(n-2)×180°(n≥3)
我们可以发现
求十边形的内角和.
已知一个多边形的内角和为900°,这个多边形是几边形?
1440
七边形
探索多边形的外角和
多边形内角的一边与_____________所组成的角叫做这个多边形的外角.
在每个顶点处取这个多边形的一个外角,它们的和叫做________________.
邻边延长线
多边形的外角和
怎样求三角形的外角和?
四边形的外角和呢?
五边形的外角和呢?
定理:任意多边形的外角和都为360°.
多边形的边数 3 4 5 6 … n
多边形的内角与外角的总和 …
多边形的内角和 …
多边形的外角和 …
540°
720°
900°
1080°
180°
360°
540°
720°
360°
360°
360°
360°
n×180°
(n-2)×180°
360°
已知六边形的各内角相等,问:各内角、外角分别是多少度?
已知多边形的内角和与外角和相等,那么它是几边形?
四边形
内角:120o
外角:60o
例2 一个六边形如图4-5.已知AB//DE,BC//EF,CD//AF.
求∠A+∠C+∠E的度数.
分析:因为两条平行线被一条直线所截,有许多等角关系,所以我们不妨连结AD试试看,如图.不难发现,∠1=∠3,∠2=∠4.由此可得本题解法.
∠FAB+∠C+∠E= ×720 ° =360 ° .
解 如图,连结AD.
∵AB//DE,CD//AF(已知),
∴∠1=∠3,∠2=∠4.
∴∠1+∠2=∠3+∠4,即∠FAB=∠CDE.
同理,∠B=∠E,∠C=∠F.
∵∠FAB+∠B+∠C+∠CDE+∠E+∠F
=(6-2) × 180 ° =720 ° ,
多边形
n边形的内角和为____________
过n边形的同一顶点可以引_______条对角线;n边形共有_______条对角线
任意多边形的外角和为_________
(n-2)×180°
360°
(n-3)
随堂演练
1.[2019·云南] 一个十二边形的内角和等于( )
A.2160° B.2080° C.1980° D.1800°
2.[2018·宁波期中] 若一个多边形的内角和等于1260°,则该多边形的边数是 ( )
A.8 B.9 C.10 D.11
D
B
3.[2018·绍兴期中] 如果n边形的内角和等于外角和的3倍,那么n的值是 ( )
A.5 B.6 C.7 D.8
4.已知一个多边形的每个内角都相等.若这个多边形的内角和为540°,则这个多边形的每一个外角等于 ( )
A.60° B.72° C.90° D.108°
D
B
同课章节目录
- 第一章 二次根式
- 1.1 二次根式
- 1.2 二次根式的性质
- 1.3 二次根式的运算
- 第二章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程的应用
- 2.4 一元二次方程根与系数的关系(选学)
- 第三章 数据分析初步
- 3.1 平均数
- 3.2 中位数和众数
- 3.3 方差和标准差
- 第四章 平行四边形
- 4.1 多边形
- 4.2 平行四边形
- 4.3 中心对称
- 4.4 平行四边形的判定
- 4.5 三角形的中位线
- 4.6 反证法
- 第五章 特殊平行四边形
- 5.1 矩形
- 5.2 菱形
- 5.3 正方形
- 第六章 反比例函数
- 6.1 反比例函数
- 6.2 反比例函数的图象和性质
- 6.3 反比例函数的应用
