浙教版数学八年级下册同步课件:1.3.3二次根式的实际应用(共18张PPT)
文档属性
| 名称 | 浙教版数学八年级下册同步课件:1.3.3二次根式的实际应用(共18张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 827.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-06-10 15:02:25 | ||
图片预览





文档简介
(共18张PPT)
第一章 二次根式
1.3 第3课时 二次根式的实际应用
知识回顾
二次根式的混合运算:
①运算种类:二次根式的_________________________________的混合运算。
②运算顺序:先算___________,再算_________,最后算________,如果有括号就先算括号里面的。
加、减、乘、除、乘方(或开方)
乘方、开方
乘除
加减
二次根式混合运算的结果应写成__________________________的形式并且分母中不含二次根式。
最简二次根式(或整式)
进行二次根式的开方运算时应使开出的因数(式)是_______________。
非负数(式)
在日常生活和生产实际中,我们在解决一些问题,尤其是涉及直角三角形的边长计算的问题时,经常用到二次根式及其运算。
获取新知
借助特殊直角三角形中边之间的关系构造方程,建立起条件与结论之间的联系,使问题得到解决.
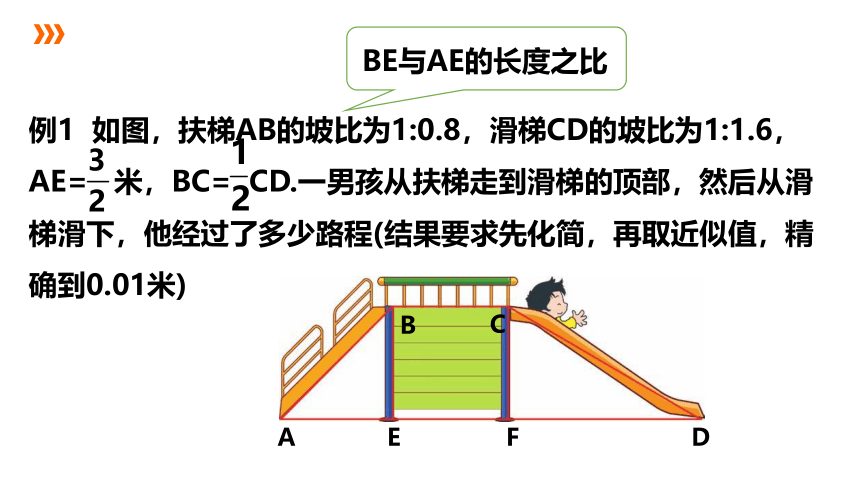
例1 如图,扶梯AB的坡比为1:0.8,滑梯CD的坡比为1:1.6,
AE= 米,BC= CD.一男孩从扶梯走到滑梯的顶部,然后从滑梯滑下,他经过了多少路程(结果要求先化简,再取近似值,精确到0.01米)
BE与AE的长度之比
A
E
F
D
B
C
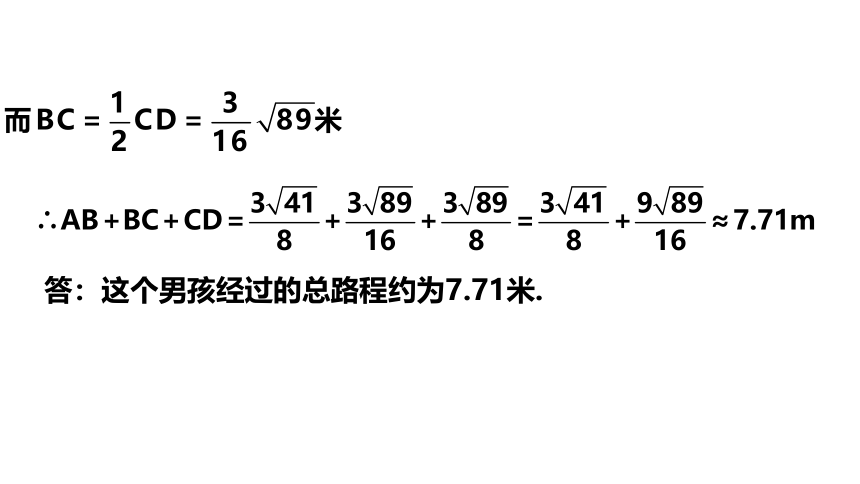
在Rt△CFD中,DF= ×1.6=3米
解:在Rt△AEB中,AE= 米,BE= ÷0.8= 米
答:这个男孩经过的总路程约为7.71米.
例2 如图是一张等腰直角三角形彩色纸,AC=BC=40cm,将斜边上的高CD四等分,然后裁出3张宽度相等的长方形纸条.
(1)分别求出3张长方形纸条的长度
解:(1)在Rt△ABC中,AC=BC=40cm,
∵ CD⊥AB,AD=BD ,
∵最上面长方形纸条的长是 CD的2倍
∴其长度为2× CD=2×5 =10 cm
2× CD=2×10 =20 cm
同理可得,其余两张长方形纸条的长度依次为:
2× CD=2×15 =30 cm
答:三张长方形纸条的长度分别为
(2)若用这些纸条为一幅正方形美术作品镶边(纸条不重叠),如图,正方形美术作品的面积为多少平方厘米.
解:(2)三张长方形纸条连接在一起的总长度为
因此,给这幅美术作品所镶的边框可以看做由四张宽为 cm,长为 cm的彩色纸条围城
则正方形的边长=
正方形的面积=
答:这幅正方形美术作品的面积为200cm2
(1)应用二次根式解决实际问题时,首先要仔细分析问题,根据题意列出算式,然后应用二次根式的性质和运算法则化简计算;
(2)当实际问题中涉及长度(距离)、高、面积等几何知识时,若题目没有给出图形,要先画出图形,必要时,可添加辅助线帮助求解.
随堂演练
1. 如图,长方形内有两个相邻的正方形,其面积分别为2和8,则图中阴影部分的面积为( )
B
2.甲、乙两名同学在广场上练习滑旱冰,两人同时从同一点出发,甲以4 m/s的速度向正南方向滑行,乙以6 m/s的速度向正东方向滑行,10 s后两人相距 ( )
D
二次根式的实际应用
坡度问题
几何问题
距离问题
基本思路:
(1)寻找或构造直角三角形;
(2)利用勾股定理进行计算
第一章 二次根式
1.3 第3课时 二次根式的实际应用
知识回顾
二次根式的混合运算:
①运算种类:二次根式的_________________________________的混合运算。
②运算顺序:先算___________,再算_________,最后算________,如果有括号就先算括号里面的。
加、减、乘、除、乘方(或开方)
乘方、开方
乘除
加减
二次根式混合运算的结果应写成__________________________的形式并且分母中不含二次根式。
最简二次根式(或整式)
进行二次根式的开方运算时应使开出的因数(式)是_______________。
非负数(式)
在日常生活和生产实际中,我们在解决一些问题,尤其是涉及直角三角形的边长计算的问题时,经常用到二次根式及其运算。
获取新知
借助特殊直角三角形中边之间的关系构造方程,建立起条件与结论之间的联系,使问题得到解决.
例1 如图,扶梯AB的坡比为1:0.8,滑梯CD的坡比为1:1.6,
AE= 米,BC= CD.一男孩从扶梯走到滑梯的顶部,然后从滑梯滑下,他经过了多少路程(结果要求先化简,再取近似值,精确到0.01米)
BE与AE的长度之比
A
E
F
D
B
C
在Rt△CFD中,DF= ×1.6=3米
解:在Rt△AEB中,AE= 米,BE= ÷0.8= 米
答:这个男孩经过的总路程约为7.71米.
例2 如图是一张等腰直角三角形彩色纸,AC=BC=40cm,将斜边上的高CD四等分,然后裁出3张宽度相等的长方形纸条.
(1)分别求出3张长方形纸条的长度
解:(1)在Rt△ABC中,AC=BC=40cm,
∵ CD⊥AB,AD=BD ,
∵最上面长方形纸条的长是 CD的2倍
∴其长度为2× CD=2×5 =10 cm
2× CD=2×10 =20 cm
同理可得,其余两张长方形纸条的长度依次为:
2× CD=2×15 =30 cm
答:三张长方形纸条的长度分别为
(2)若用这些纸条为一幅正方形美术作品镶边(纸条不重叠),如图,正方形美术作品的面积为多少平方厘米.
解:(2)三张长方形纸条连接在一起的总长度为
因此,给这幅美术作品所镶的边框可以看做由四张宽为 cm,长为 cm的彩色纸条围城
则正方形的边长=
正方形的面积=
答:这幅正方形美术作品的面积为200cm2
(1)应用二次根式解决实际问题时,首先要仔细分析问题,根据题意列出算式,然后应用二次根式的性质和运算法则化简计算;
(2)当实际问题中涉及长度(距离)、高、面积等几何知识时,若题目没有给出图形,要先画出图形,必要时,可添加辅助线帮助求解.
随堂演练
1. 如图,长方形内有两个相邻的正方形,其面积分别为2和8,则图中阴影部分的面积为( )
B
2.甲、乙两名同学在广场上练习滑旱冰,两人同时从同一点出发,甲以4 m/s的速度向正南方向滑行,乙以6 m/s的速度向正东方向滑行,10 s后两人相距 ( )
D
二次根式的实际应用
坡度问题
几何问题
距离问题
基本思路:
(1)寻找或构造直角三角形;
(2)利用勾股定理进行计算
同课章节目录
- 第一章 二次根式
- 1.1 二次根式
- 1.2 二次根式的性质
- 1.3 二次根式的运算
- 第二章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程的应用
- 2.4 一元二次方程根与系数的关系(选学)
- 第三章 数据分析初步
- 3.1 平均数
- 3.2 中位数和众数
- 3.3 方差和标准差
- 第四章 平行四边形
- 4.1 多边形
- 4.2 平行四边形
- 4.3 中心对称
- 4.4 平行四边形的判定
- 4.5 三角形的中位线
- 4.6 反证法
- 第五章 特殊平行四边形
- 5.1 矩形
- 5.2 菱形
- 5.3 正方形
- 第六章 反比例函数
- 6.1 反比例函数
- 6.2 反比例函数的图象和性质
- 6.3 反比例函数的应用
